基于热流量积分的混凝土温控水管冷却边界模拟算法

朱振泱，刘敏芝，强 晟，相建方

（1. 中国水利水电科学研究院流域水循环模拟与调控国家重点实验室，北京 100038；2. 鄞州区水利工程质量与安全监督站，宁波 315100； 3. 河海大学水利水电工程学院，南京 210098）

基于热流量积分的混凝土温控水管冷却边界模拟算法

朱振泱1，刘敏芝2，强 晟3，相建方1

（1. 中国水利水电科学研究院流域水循环模拟与调控国家重点实验室，北京 100038；2. 鄞州区水利工程质量与安全监督站，宁波 315100； 3. 河海大学水利水电工程学院，南京 210098）

以往用冷却水管离散模型迭代计算混凝土温度场时，水管边界被近似认为是第三类边界条件，此类边界条件的参数获取要通过试验并进行反演，试验费用较大且有时候可靠性不高。针对该问题，在热量平衡条件的基础上提出由与水管接触混凝土的热流量、水管的导热系数、管壁厚度和水管内壁温度推算水管外壁温度的新算法，并对原有迭代方法进行改进，解决迭代次数多和迭代可能无法收敛的问题。对比算例中，采用传统算法，模型边界处的误差可达到1.67℃，而采用该新算法，误差仅为0.3℃。应用所提方法对某混凝土块施工期混凝土温度场进行了仿真计算，计算值与实测值吻合较好，且迭代收敛速度较快，一般的迭代方法，需要迭代15次，而采用改进的迭代方法，只需迭代7次即可以达到稳定值。该算法能明确通水冷却的边界条件，节省试验费用，提高计算效率，有较好的工程应用价值。

温度；模型；混凝土；迭代算法

0 引言

温度应力导致的裂缝为混凝土施工期最常见的裂缝，近年来很多学者对此进行了持续深入的研究。冷却水管是控制混凝土温度应力的有效措施，近年来广泛应用于工程实践中[1-4]。

目前普遍认为，金属水管内壁和外壁的温差可以忽略，但塑料水管必须考虑内外壁温差的影响。塑料水管内部的温度场分布较为复杂，虽然有学者认为塑料管内温度可以等效为线性分布，即塑料管内的温度梯度为常数[5-6]；但有关文献和本文的研究成果均表明塑料水管内部的温度梯度非线性分布，不应用常数表示[7]。以往含离散水管模型的大体积混凝土温度场迭代计算中，一般将塑料水管边界作为第三类边界条件，在这种条件下温度场计算精度与管壁放热系数的取值有密切关系。不同的水管材质、管壁厚度、水的流速、沿程水温条件下，管壁放热系数均有可能不同。由于管壁放热系数对温度场的影响较大，目前往往要通过现场试验反演计算获得，耗费的成本较大[8]。且目前用等效的放热系数一个参数来涵盖管壁导热系数、管壁厚度和管壁表面温度梯度等多个物理量综合产生的效果，有时候可靠性不高。

目前大体积混凝土通水冷却模型方面的研究较为丰富，许多专家都提出了各自的模型:等效算法[7]、子结构算法[9-10]、埋置单元法[11]、模拟混凝土水管冷却效应的直接算法[12]、扩展有限元法[13]。目前用于含水管大体积混凝土温度场的算法中，如不考虑水管周围混凝土的温度场，则计算量小，如朱伯芳的等效算法在混凝土坝的温控防裂中应用广泛[7]。离散水管模型的混凝土温度场迭代算法是由朱伯芳院士提出，并由朱岳明教授进行改进并推广，目前已经广泛应用于各种薄壁结构中，但在大坝中仍属于初步的应用[7,14-17]。该计算方法计算精度较高，且能很好地模拟工程现场的“蛇形水管”布置形式。但是节点数量庞大，计算速度慢，对计算机的性能要求较高，目前多用于诸如水闸等薄壁结构中。由于混凝土通水冷却时，塑料水管对混凝土薄壁结构温度场和应力场影响较大，只有准确考虑其影响才能对薄壁结构温度场和应力场进行可靠分析[18-19]。故针对塑料水管内温度和温度梯度分布以及塑料管对混凝土冷却效果的进一步研究是十分有必要的。

本文根据热平衡原理，推导了水管内外壁的温度关系式。由沿程水温（沿水流方向水管内壁的温度）、与水管接触混凝土的热流量、管壁导热系数及管壁厚度即可以推算出水管外壁温度（水管与混凝土的接触面）。由于水管和混凝土紧密接触，可以认为接触面的热阻很小，故在计算中将水管外壁的温度作为第一类边界条件。由于水管的导热系数和水管的材质有很大关系，同种材质的水管，导热系数相差不大，而有些水管在出厂时就标明了导热系数。管壁的厚度可以通过简单测量获取。因此水管的导热系数和管壁的厚度均可轻易获取，而沿程水温、与水管接触混凝土的热流量也可以在计算中获取，因此该边界条件处理方法可以避免将管壁作为第三类边界条件而需要通过试验和反演获取表面放热系数的缺陷，提高了经济性及可靠性。

目前的最新研究成果表明，采用离散迭代算法时，即使在网格数量较少的情况下，如选择最佳热流量断面进行热流量积分，依然能得到热流量的精确解答[20-22]。以上研究成果表明，采用热流量积分法计算塑料水管通水冷却作用不需要增加额外网格节点的数量，是完全可行的。但应用该边界条件处理方法和传统的水管冷却离散迭代算法计算温度场，会增加迭代次数，甚至出现迭代不收敛的现象，需要改进。基于以上分析，本文对混凝土温控冷却水管边界模拟方法进行深入研究，拟提出一种精确快速计算方法解决这些问题。

1 基本理论和方法

1.1 不稳定温度场的计算原理

在混凝土计算域R内任何一点处，不稳定温度场T满足以下热传导控制方程，

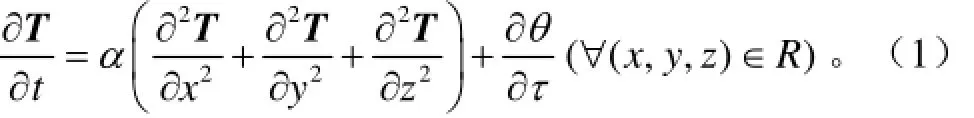
式中T为温度，℃；α为导温系数，m2/d；θ混凝土热量释量，℃；t和τ分别表示时间和龄期，d；R为计算域。

1.2 水管沿程水温计算

根据热传导平衡条件，水管内沿程水温增量可以用以下方程表示[7,15]

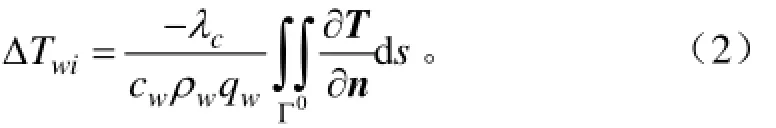
式中cλ为混凝土的导热系数，kJ/m·d·℃；cw为冷却水比热，kJ/kg·℃；ρw为冷却水的密度，kg/m3；qw为冷却水流量，m3/d；n为热流量积分面的外法向向量。

1.3 热流量积分的最佳断面

本文所提的方法依赖于热流量的计算，如果仅采用式（2）计算热流量，在没有选择合适的积分断面的情况下，只有在网格十分密集的情况下，才能得到精确解，需要大量的计算节点。同样，采用式（2）计算沿程水温，需要十分密集的网格才能得到精确解，如果采用稀疏的网格计算沿程水温则计算结果将明显小于实际沿程水温。为此，采用最佳热流量积分法可解决该问题[20-21]，基本原理如下：

如将S1面定义为水管和混凝土单元A的交界面，S2面定义为混凝土单元A和另一个混凝土单元的交界面。将ζ=−1和ζ=1分别代表S1面和S2面；根据文献[20-21]的研究结果，对于8节点的六面体单元，S1面的温度梯度计算值小于真实值，而S2面的温度梯度计算值大于真实值，只有S3面（ζ=0.4）的温度梯度的计算值与真实值相符。因此，只有采用S3面（ζ=0.4）作为热流量积分，才能得到真实的热流量，为热流量积分的最佳断面。

2 含水管离散模型的混凝土温度场迭代计算方法

2.1 水管内壁和外壁温差计算

图1为水管垂直于水流方向截面的一部分，该部分的弧度为θ，内壁弧长为la，水管顺水流方向的长度为dn，水管的内径为ra，水管的外径为rd，rx是某点到水管中心的距离。Na为该部分水管内壁的温度梯度，Nx是该部分水管内某点（与水管中心的距离为rx）的温度梯度，λ为水管材料的导热系数，由于水和混凝土温差较大，故可以认为在水管的任意位置温度梯度方向均与水管壁垂直，故在dt时间内通过该段水管内壁和距离水管中心长度为rx截面（图1中的X截面）的热流量分别为：

图1 一个典型水管垂直于水流方向截面Fig.1 A pipe section in direction perpendicular to water flow

同样，由于水和混凝土温差较大，可以认为在水管的任意位置温度梯度方向均与水管壁垂直，故dt时间内流过该部分水管内壁和图1中流过X截面的热量相等，故有。因此，，设水管内壁的温度为Tin，水管外壁的温度为Tou。根据积分，则有，故

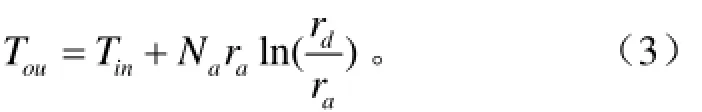
式中ra为水管的内径，m；rd为水管的外径，m；Na为该水管微段水管内壁的温度梯度，℃/m；Tin和Tou分别为内壁与外壁的温度，℃。

计算时将水管分为m段，设第i段水管长度为dn，单位时间dt内由水管附近混凝土传给该段水管的热量为Q。根据热流量守恒定则，Q与dt时间内流经水管内壁的热量相等，故有，故

式中λ为水管材料的导热系数，kJ/m·d·℃；dn为计算微段水管长度，m；Q为时间dt内由水管附近混凝土传给该段水管的热量kJ/m；la为内壁弧长，m。

故水管内壁和水管外壁的温差为

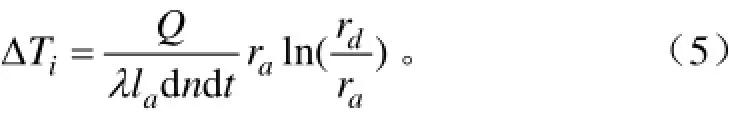
2.2 沿水流方向水管外壁温度分布

由于冷却水的入口温度已知，利用公式（2）在最佳的热流量积分断面上做热流量积分，对每根水管沿水流方向可以逐段推求出沿程水温。计算时根据需要将水管分为m段，则第i段所在位置的沿程水温Twi为式中进口水温为Tw0，℃；ΔTwj为沿程水管微段水温的增量，℃。

水管内壁直接与水接触，因此可以认为水管内壁的温度即为水温。由公式（5）和公式（6）可知水管外壁的温度Touwi为

式中ΔTi为水管内壁和外壁的温差，℃。

在式（2）中，水管沿程水温的变化与温度梯度有关，是一个边界非线性问题，温度场无法一步求出，必须采用迭代求解法逐步逼近真实解[7,15]。第一次迭代时可以假定整个冷却水管沿程的内壁和外壁的温度均等于冷却水的入口温度，利用式（1）求出温度场的近似解，再利用式（2）、式（6）和式（7）求出沿水流方向水管内壁的温度分布和沿水流方向水管外壁的温度分布，重复以上过程直到获得稳定解。

当管壁材料为铁管时，沿程水温十分接近铁管外壁的温度，采用上述方法计算大体积混凝土温度场，一般迭代7次以内就可以获得稳定解。而当水管材料为塑料时，水管内外壁温差很大，甚至可达到5.0℃以上。沿程水温变化对管外壁温度的影响很大，只有精确求出水管沿程水温才能获得精确解。采用上述方法迭代，计算结果将迭代很多次以后才能收敛，甚至无法收敛。

2.3 温度场的迭代算法改进

由于第一次迭代前水管内外壁的温度均等于水管进口温度，小于稳定解。因第一次迭代计算出的水管内外壁的温度梯度将大于稳定解，故第一次迭代计算出的水管内外壁的温度也将高于稳定解。而第二次迭代前水管内外壁温度即为第一次迭代后的水管内外壁温度，故第二次迭代计算出的水管内外壁温度和温度梯度都将低于稳定解。同理，第奇数次迭代计算出的水管内外壁温度和温度梯度都将大于稳定解，而第偶数次迭代计算出的水管内外壁温度和温度梯度都将小于稳定解。

设第（N-1）次迭代后的管外壁温度为Tn1−，第N次迭代后的管外壁温度为Tn，作为第（N+1）次迭代前的管外壁温度，则计算结果更容易接近于稳定解，收敛的速度也将提高。一般情况下，采用改进后的迭代算法计算大体积混凝土温度场时，迭代8次以内误差即可以控制在0.1℃以内。

2.4 迭代收敛条件的数学依据

当计算到第i步的第n次迭代结束时，根据式（3），以下关系式成立，则

式中Toun和Tin分别表示第n次迭代计算结束后某个水管微段的水管外壁和内壁的温度；Nn表示第n次迭代计算结束后得到的水管内壁的温度梯度。

以往的研究成果表明，传统的离散迭代算法具有较好的收敛性[7,15]；此处只要证明采用该新方法不会增大迭代难度，即可证明该新方法也具有较好的迭代收敛性能。Tin虽然在迭代过程中也是个变量，由于该处只分析新方法对迭代的影响，故假设Tin是恒定的，那么

设Tour为真实的水管外壁温度。如果将第n次迭代的计算结果作为第（n+1）次迭代的初始条件，那么，根据第2.3节的分析结果，当当。因此，由于当时，是负数；而时，是正数。故如果足够小，Tn+1总是向Tr逐渐逼近的。

3 算法对比分析

本节将传统算法、新算法分别和理论解对比（将水管也作为实体单元剖分的有限元法），并分析新算法具有更高的精度。

传统的模型用等效放热系数模拟水管的边界条件且未采用合理的热流量积分。由于未考虑热流量积分造成沿程水温偏低，目前许多工程采用较小的表面放热系数模拟水管边界，如采用β=3 000 kJ/(m·d·℃)模拟（甚至更小），此时会造成计算上的误差（例如进出水口附近冷却效果计算不准确等）。

该算例为1.5 m×1.5 m×5 m的混凝土块，中间埋置冷却水管（如图2所示）。浇筑后即开始冷却，除水管边界外，其余边界条件均为绝热边界，水温15℃。混凝土绝热温升为，等效放热系数为β=3 000 kJ/(m·d·℃)，水管的内直径和外直径分别为28和32 mm。

图2 有限单元网格Fig.2 Finite element mesh

通水冷却10 d进口附近切面的温度分布如图3所示。根据计算结果，离混凝土较远的水管绝热边界处，该算例下传统算法的误差可达1.67℃，而新算法的误差仅为0.3℃。

图3 浇筑10 d时断面的温度分布Fig.3 Temperature distribution on section 10 d after placement

4 工程算例

4.1 基本资料

某混凝土试验块于2009年9月份施工，该混凝土块长27.0 m，宽15.0 m，高3.0 m。分两层浇筑，每层高度为1.5 m，间歇时间为4 d。

浇筑温度控制在18.0℃。距离地面0.75和2.25 m处分别布置两根塑料冷却水管，水管的水平间距1.5 m，各层混凝土开始浇筑后1.75 d通水。通水时间21.0 d，冷却水初温为8.5℃，通水12.0 d后水温调整为15.0℃，通水流量均为35.0 m3/d。计算中，气温取实测值，浇筑块表面覆盖一层大坝保温被。浇筑块及地基的有限单元网格如图4所示。特征点平面位置、水管水平布置和水流方向如图5所示，水流方向始终未变。

图4 有限单元网格Fig.4 Finite element mesh

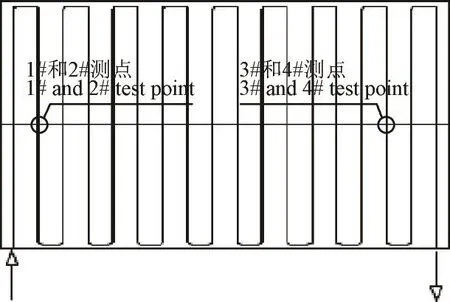
图5 水管平面布置和水流方向Fig.5 Layout of cooling pipe and water flow direction

混凝土的绝热温升曲线可以用以下公式表示

式中θ为绝热温升终值，℃，材料的其他热学参数见表1。

表1 其他热学参数Table 1 Other thermal parameters

4.2 计算结果分析

1）计算结果与实测数据对比

测点1和测点2位于水管的进水口附近。测点1距离水管8 cm，测点2距离水管12 cm。受气温波动的影响，进口水温很难保持稳定，实际施工过程中冷却水流量有时候也会出现小幅波动，所以实测值的历时曲线并不光滑。总体来看，计算值和实测值较为吻合。测点3和测点4位于水管的出口附近。测点3距离水管8 cm，测点4距离水管12 cm。由于流量较小且水管较长，受沿程水温（进出口水温差在10℃左右）影响，点3和点4的温度要明显高于点1和点2的温度（见图6），水温的改变对点3和点4的温度影响也较点1和点2小。故在实际施工中，定期改变通水的方向是很有必要的。

2）温度场计算结果分析

图7为沿水流方向水管内壁和外壁的平均温差分布。因进口水温较低，进口处的管内外壁温差也大于出口处。

3）两种不同迭代方法对比

采用一般的迭代方法，需要迭代15次，沿程水温才能达到稳定值（误差小于0.08℃）。而采用笔者改进的迭代方法，只需迭代7次即可以达到稳定值。

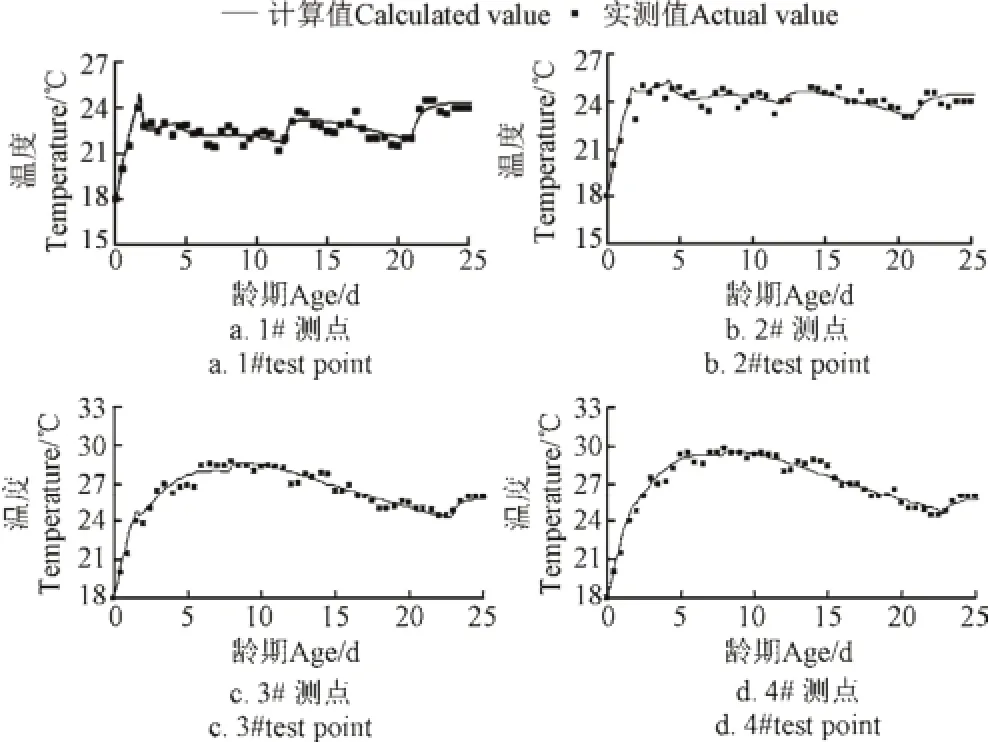
图6 计算值和实测值对比Fig.6 Comparison between calculation value and actual value

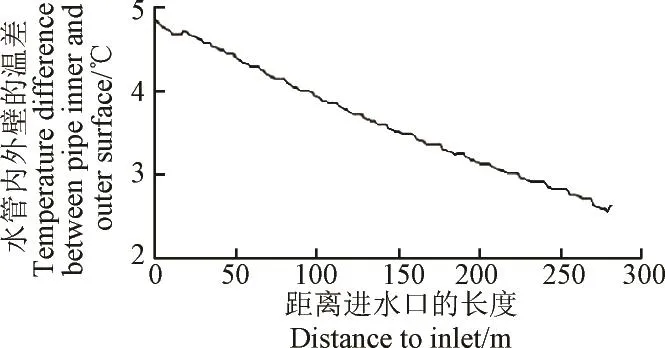
图7 管内外壁温差沿水流方向分布Fig.7 Temperature difference distribution between inner and outer surface along pipe

5 结论

由于经济和施工方便等原因，塑料水管越来越广泛地应用于各类大体积混凝土温控防裂中。在以往含离散水管模型的大体积混凝土温度场迭代计算中，塑料水管边界往往考虑成第三类边界条件，在这种条件下温度场计算的精度与水管管壁放热系数有很大的关系。本文根据热平衡原理，推导了水管内外壁的温度关系。由沿程水温（沿水流方向水管内壁的温度）、与水管接触混凝土的热流量、水管的导热系数及管壁厚度，即可推算出水管外壁温度（水管和混凝土的接触面），然后在计算中可将水管外壁的温度作为第一类边界条件。水管的导热系数及管壁的厚度均可轻易获取，而沿程水温、与水管接触混凝土的热流量也可以在计算中获取。从而避免了将管壁作为第三类边界条件要通过试验和反演获取管壁放热系数以及可靠性较差的缺点。对比算例中，如采用传统算法，模型边界处的误差达到1.67℃，而采用该新算法，误差仅为0.3℃。工程算例表明：采用这种新的塑料水管边界条件的处理方法，测点的温度能与实测值吻合得较好。此外，笔者在原有迭代方法的基础上还进行了改进，提高了收敛速度，节约了计算时间；本文的工程算例中，采用一般的迭代方法，需要迭代15次，而采用改进的迭代方法，只需迭代7次即可以达到稳定值。

[1] 强晟，郑伟忠，张勇强，等. 基于改进微粒群法和有限元法的混凝土温控方案优化[J]. 农业工程学报，2014，30(16)：75－83. Qiang Sheng, Zheng Weizhong, Zhang Yongqiang, et al. Optimization of concrete temperature control measures based on improved particle swarm optimization and finite element method[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2014, 30(16): 75－83. (in Chinese with English abstract)

[2] Zhu Zhenyang, Qiang Sheng, Chen Weimin. A model for temperature influence on concrete hydration exothermic rate (part one: theory and experiment)[J]. Journal of Wuhan University of Technology (Materials Science Edition), 2014, 29(3): 540－545.

[3] Wang Haibo, Qiang Sheng, Zhu Zhenyang. The whole process simulation and research on temperature field and thermal stress for large sluice pier[J]. Advanced Materials Research, 2011(163/164/165/166/167): 259－263.

[4] Zhu Zhenyang, Qiang Sheng, Liu Minzhi. Cracking mechanism of long concrete bedding cushion and prevention method[J]. Advanced Materials Research, 2011(163/164/165/166/167): 880－887.

[5] Chen Shenhong, Su Peifang, et al. Composite element algorithm for the thermal analysis of mass concrete simulation of cooling pipes[J]. International Journal of Numerical Methods for Heat & Fluid Flow, 2011, 21(3/4): 434－447.

[6] 苏培芳，陈胜宏，田甜. 混凝土水管冷却的复合单元算法[J].武汉理工大学学报，2010，32(24)：48－53. Su Peifang, Chen Shenghong, Tian Tian. Preliminary research on composite element algorithm for the concrete containing cooling pipes[J]. Journal of Wuhan University of Technology, 2010, 32(24): 48－53. (in Chinese with English abstract)

[7] 朱伯芳. 论混凝土坝的水管冷却[J]. 水利学报，2010，41(5)：505－513. Zhu Bofang. On pipe cooling of concrete dams[J]. Journal of Hydraulic Engineering, 2010, 41(5): 505－513. (in Chinese with English abstract)

[8] 王振红，张国新，刘毅，等. 混凝土水管冷却试验与温控参数的反分析[J]. 四川大学学报：工程科学版，2011，43(3)：56－60. Wang Zhenhong, Zhang Guoxin, Liu Yi, et al. Test and inverse analysis for temperature control parameters of concrete with cooling pipe[J]. Journal of Sichuan University (Engineering Science Edition), 2011, 43(3): 56－60. (in Chinese with English abstract)

[9] 刘宁，刘光廷. 水管冷却效应的有限元子结构模拟技术[J].水利学报，1997(12)：43－49. Liu Ning, Liu Guangting. Sub-structural FEM for the thermal effect of cooling pipes in mass concrete structures[J]. Journal of Hydraulic Engineering, 1997(12): 43－49. (in Chinese with English abstract)

[10] 颉志强，强晟，许朴，等. 水管冷却混凝土温度场和应力场计算的有限元子结构法[J]. 农业工程学报，2011，27(5)：13－18. Xie Zhiqiang, Qiang Sheng, Xu Pu, et al. Finite element substructure method for calculation of pipe cooling concrete thermal field and stress field[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2011, 27(5): 13－18. (in Chinese with English abstract)

[11] 陈国荣，许文涛，杨昀，等. 含冷却水管大体积混凝土温度场计算的一种新方法[J]. 计算物理，2012，29(3)：411－416. Chen Guorong, Xu Wentao, Yang Yun, et al. Computation method for temperature field of mass concrete containing cooling water pipes[J]. Chinese Journal of Computaitonal Physics, 2012, 29(3): 411－416. (in Chinese with English abstract)

[12] 刘晓青，李同春，韩勃. 模拟混凝土水管冷却效应的直接算法[J]. 水利学报，2009，40(7)：892－896. Liu Xiaoqing, Li Tongchun, Han Bo. Direct algorithm for simulating cooling effect of water pipes in concrete[J]. Journal of Hydraulic Engineering, 2009, 40(7): 892－896. (in Chinese with English abstract)

[13] Zuo Zheng, Hu Yu, Li Qingbin, et al. An extended finite element method for pipe-embedded plane thermal analysis[J]. Finite Elements in Analysis and Design, 2015(102/103): 52－64.

[14] 强晟，朱岳明，丁兵勇，等. 基于冷却水管离散算法的重力坝温控研究[J]. 水利能源科学，2008，26(5)：93－95. Qiang Sheng, Zhu Yueming, Ding Bingyong, et al. Study on temperature control of gravity dam based on explicit algorithm for cooling pipe[J]. Water Resources and Power, 2008, 26(5): 93－95. (in Chinese with English abstract)

[15] 朱岳明，徐之青，贺金仁，等. 混凝土水管冷却温度场的计算方法[J]. 长江科学院学报，2003，20(2)：19－22. Zhu Yueming, Xu Zhiqing, He Jinren, et al. A calculation method for solving temperature field of mass concrete with cooling pipes[J]. Journal of Yangtze River Scientific Research Institute, 2003, 20(2): 19－22. (in Chinese with English abstract)

[16] 许朴，朱岳明，贲能慧. 倒T型混凝土薄壁结构施工期温度裂缝控制研究[J]. 水利学报，2009，40(8)：969－975. Xu Pu, Zhu Yueming, Ben Nenghui. Study on thermal cracking control of inverted T-shaped concrete structures during construction[J]. Journal of Hydraulic Engineering, 2009, 40(8): 969－975. (in Chinese with English abstract)

[17] 王振红，朱岳明，于书萍，等. 水闸闸墩施工期温度场和应力场仿真计算分析[J]. 天津大学学报，2008，41(4)：476－481. Wang Zhenhong, Zhu Yueming, Yu Shuping, et al. Simulation and analysis of temperature field and stress field of sluice pier concrete during construction[J]. Journal of Tianjin University, 2008, 41(4): 476－481. (in Chinese with English abstract)

[18] 朱振泱，强晟，郑占强，等. 用遗传算法确定考虑温度历程的混凝土水化放热模型参数及试验验证[J]. 农业工程学报，2013，29(1)：86－92. Zhu Zhenyang, Qiang Sheng, Zheng Zhanqiang, et al. Determination of parameters for hydration exothermic model considering concrete temperature duration by genetic algorithm[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2013, 29(1): 86－92. (in Chinese with English abstract)

[19] Hattel J H, Thorborg J. A numerical model for predicting the thermal mechanical conditions during hydration of early age concrete[J]. Applied Mathematical Modeling, 2003, 27(1): 1－26.

[20] Zhu Zhenyang, Qiang Sheng, Chen Weimin. A new method solving the temperature field of concrete around cooling pipes[J]. Comput. Concrete, 2013, 11(5): 441－462.

[21] 朱振泱，强晟，陈炜旻，等. 含水管混凝土温度场的改进离散迭代算法[J]. 应用基础与工程科学学报，2014，22(3)：492－500. Zhu Zhenyang, Qiang Sheng, Chen Weimin, et al. Improvement on iteration method solving temperature field of mass concrete with pipes[J]. Journal of Basic Science and Engineering, 2014, 22(3): 492－500. (in Chinese with English abstract)

[22] 张军，段亚辉. 混凝土冷却水管的有限元沿程水温改进算法[J]. 华中科技大学学报：自然科学版，2014(2)：56－58. Zhang Jun, Duan Yahui. FEM analysis of concrete with cooling pipes using an improved method on the calculation of water temperature along the pipes[J]. J. Huazhong Univ. of Sci. & Tech: Natural Science Edition, 2014(2): 56－58. (in Chinese with English abstract)

Algorithm to simulate concrete temperature control cooling pipe boundary based on heat flux integration

Zhu Zhenyang1, Liu Minzhi2, Qiang Sheng3, Xiang Jianfang1
(1. State Key Laboratory of Simulation and Regulation of Water Cycle in River Basin, China Institute of Water Resources and Hydropower Research, Beijing 100038, China; 2. Yinzhou District Quality and Safety Supervision Station of Water Conservancy Projects, Ningbo 315100, China; 3. College of Water Conservancy and Hydropower Engineering, Hohai University, Nanjing 210098, China)

When using the explicit iterative method to solve the temperature of mass concrete with cooling pipes, it is generally considered that the inner and outer surface of metal pipes can be neglected but the temperature difference cannot be neglected when using the plastic pipes. And the plastic pipes are usually regarded as the third boundary condition. For the past researchers, the coefficient of this kind of boundary condition can be got by experiment and inversion, which is yet expensive and may also not be reliable sometimes. To solve the problem, on the base of heat balance condition, a new calculation method is brought forward. It is well known that concrete is a poor conductor of heat, and there is a large temperature difference between the concrete and the cooling water. So, in the shell of a cooling pipe and the concrete near it, it can be assumed that the heat flux is only discharged by cooling water in the pipe and the direction of the temperature gradient is perpendicular to the cooling pipe surface. So, the heat fluxes passing through any circle (take the center pipe as the center of those circles) in the shell of the plastic pipe are equal. Based on these basic principles, the temperature of cooling pipe outer surface can be obtained by the heat flux of the concrete around the pipe, the thermal conductivity, the thickness of the pipe and the temperature of pipe inner surface. When using the conventional iterative method to solve the temperature of the mass concrete with cooling pipes, the iterative method should be used for the unknown water temperature distributions along the cooling pipes. For this new method, the temperature distributions along the inner surface of the pipes is also unknown, so the iterative method should be also used. With this new method, when using the conventional iterative method, the convergence speed is relatively low, or even can not converge. To solve this problem, the iterative algorithm is also improved. When the iteration time is (N-1) and N separately, it is assumed that the corresponding calculated temperature on the outer surface of the cooling pipe is Tn-1and Tnrespectively. And then, when using 0.5(Tn-1+ Tn) as the initial calculation condition for the (N+1)thtime, the convergence of the iteration can be easily achieved. The convergence condition of the improved method was proved by mathematical deduction, and the deduction results showed that the convergence could be always reached in different engineering cases. A comparing numerical example was used to comparing the accuracy of the new method and the conventional explicit iterative method. In this comparing numerical example, the calculation results of the finite element method (FEM) considering the pipe as a part of mesh were considered as the theoretical solution. The calculation results showed that in the concrete near adiabatic boundary of the mesh in the comparing example, the temperature difference between the calculation result of conventional explicit iterative method and the theoretical solution was 1.67℃ , and the temperature difference between the calculation result of improved method and the theoretical solution was only 0.3℃ . So, the improved method can be more accurate than the conventional explicit iterative algorithm. Using these new achievements, the temperature field of a concrete block during construction period was simulated, and the calculation results and testing results were compared. The total number of the iteration times was 15 for the conventional iterative method and only 7 for the improved method in this engineering example. The results show that the calculation value is close to the actual value, and this algorithm has high convergence speed. So this method can be used in engineering projects to prevent mass concrete from cracking.

temperature; models; concrete; iterative algorithm

10.11975/j.issn.1002-6819.2016.09.012

TV315

A

1002-6819(2016)-09-0083-07

朱振泱，刘敏芝，强 晟，相建方. 基于热流量积分的混凝土温控水管冷却边界模拟算法[J]. 农业工程学报，2016，32(9)：83－89.

10.11975/j.issn.1002-6819.2016.09.012 http://www.tcsae.org

Zhu Zhenyang, Liu Minzhi, Qiang Sheng, Xiang Jianfang. Algorithm to simulate concrete temperature control cooling pipe boundary based on heat flux integration[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2016, 32(9): 83－89. (in Chinese with English abstract) doi：10.11975/j.issn.1002-6819.2016.09.012 http://www.tcsae.org

2015-12-22

2016-03-14

国家自然科学基金资助项目（51409264，51509020，51209219）

朱振泱，男，福建三明人，中国水利水电科学研究院高级工程师，主要从事混凝土温控防裂研究和大体积混凝土温度裂缝扩展研究。北京 中国水利水电科学研究院流域水循环模拟与调控国家重点实验室，100038。Email：1219921552@qq.com