《高等代数》课程中矩阵初等变换方法的应用
2016-12-19林大华戴立辉
林大华,戴立辉
(闽江学院 数学系,福建 福州 350108)
《高等代数》课程中矩阵初等变换方法的应用
林大华,戴立辉
(闽江学院 数学系,福建 福州 350108)
矩阵初等变换是高等代数研究及解决问题的一个很重要的工具,在高等代数课程中应用的范围很广.综述矩阵初等变换在多项式、行列式、线性方程组、二次型、线性空间、等《高等代数》课程的主要内容中的应用.
矩阵;初等变换;多项式;行列式;线性方程组;二次型;线性空间
矩阵初等变换是《高等代数》课程的一个重要组成部分,在该课程中有着特殊的地位与作用,是研究探讨该课程的一个重要工具和手段,该课程中的许多内容都可用矩阵初等变换方法给予讨论与解决.本文主要综述矩阵初等变换在多项式、行列式、线性方程组、二次型、向量空间等《高等代数》课程的主要内容中的作用,从中可以看到,掌握了矩阵初等变换方法就等于掌握了《高等代数》课程的主要方法.本文所讨论的问题均在数域P中进行.
下列变换称为矩阵初等行(列)变换,统称矩阵初等变换.
1.换法变换:交换矩阵的两行(列);2.倍法变换:用非零数乘矩阵的某一行(列);3.消法变换:矩阵的某一行(列)乘一个数加到另一行(列).
1 矩阵初等变换在多项式中的应用
可用矩阵初等变换求多项式f(x),g(x)的最大公因式,主要有以下方法:
2 矩阵初等变换在行列式中的应用
每一个n阶行列式都可看作是一个n阶方阵A的行列式,当方阵A实施一次初等变换化为n阶方阵B时,由行列式的性质可知|A|与|B|最多相差一个常数因子,而这个常数因子是可确定的.由此可得求行列式|A|方法如下:(1)用矩阵初等变换将矩阵A化为三角形矩阵B,而B的行列式|B|就等于主对角线上元素的乘积,从而求出|A|.(2)先用矩阵初等变换将矩阵A化为某一行(列)仅有一个元素非零,然后在按这一行(列)展开行列式|A|,将高阶行列式|A|降为低阶行列式,从而求出|A|.
3 矩阵初等变换在矩阵中的应用
用A表示m×n矩阵,则经初等行变换A可化为行阶梯形矩阵[3]

再经若干次初等列变换可化为矩阵A的标准形[4]
1.求矩阵的秩:对m×n矩阵A,实施初等变换将A化为阶梯形矩阵,则这个阶梯形矩阵中非零行的个数就是矩阵A的秩.
2.求矩阵的标准形:任意上m×n矩阵A都可经初等变换化为标准形其中r是矩阵的秩.
3.求可逆矩阵的逆矩阵:设A是n阶可逆矩阵,可用以下方法求A-1.(1)构造矩阵(A E),则该矩阵可经初等行变换化为(E A-1).(2)构造矩阵,则该矩阵可经初等列变换化为
4.求解矩阵方程:设A是n阶可逆矩阵,则矩阵方程AX=B(XA=B)的解是:X=A-1B(X=BA-1),于是可用以下方法求矩阵方程AX=B(XA=B)的解.
(1)构造矩阵(A B),则该矩阵可经初等行变换化为(E A-1B).
4 矩阵初等变换在线性方程组中的应用
其中A=(aij)m×n∈Pm×n,b=(b1,b2,…,bm)T∈Pm,X=(x1,x2,…,xn)T
可用矩阵初等变换方法讨论线性方程组AX=b是否有解,并在有解的情况下求出解.具体方法如下[3]:

(1)当dr+1≠0时,线性方程组无解.(2)当dr+1=0且r=n时,线性方程组有唯一解,其解为:xi=di(i=1,2,…,n)(3)当dr+1=0且r n元二次型可以用矩阵表示为f(x1,x2,…,xn)=XTAX其中A=(aij)n×n是对称矩阵,X=(x1,x2,…,xn)T.矩阵A(aij)n×n称为二次型的矩阵,它的对角线上元素aii是xi2的系数,而aij=aji(i≠j)是xixj系数的一半. 可用矩阵初等变换化二次型XTAX为标准形,主要方法有: 2.构造矩阵(A E),然后对A做同类型的初等行与列变换,而对E只做其中的初等行变换,把A变为对角矩阵B时,E就变为CT,则有CTAC=B[5]. 3.构造矩阵(A E),然后对其做行的消法变换,当把A化为上三角矩阵D时,E就变为CT,则有CTAC=diag(b11,b22,…,bnn),其中bii(i=1,2,…,n)是D的主对角线上的元素[6]. 于是只需做非退化线性替换X=CY,就把二次型XTAX化为标准形YTBY. 1.判断一个向量能否由一个向量组线性表示:设α1,α2,…,αm,β∈Pn,以这些向量为列构造矩阵(α1α2… αmβ),用矩阵初等行变换将这个矩阵化为 (1)当dr+1≠0时,向量β不能由α1,α2,…,αm线性表示.(2)当dr+1=0时,向量β能由α1,α2,…,αm线性表示,且表示式为β=d1α1+d2α2+…+drαj 2.判断一个向量组能否由另一个向量组线性表示: 设α1,α2,…,αm,β1,β2,…,βi∈Pn以这些向量为列构造矩阵 用矩阵初等行变换将这个矩阵化为 (1)当d(r+1)1,d(d+1)2,…,d(d+1)t不全为零时,β1,β2,…,βt不能由α1,α2,…,αm线性表示.(2)当d(r+1)1=d(d+1)2=…=d(d+1)t=0时,β1,β2,…,βt能由α1,α2,…,αm线性表示.且表示式为 3.判断一个向量组是否线性相关:设α1,α2,…,αm∈Pn,以这些向量为列构造矩阵(α1α2… αm),用矩阵初等行变换将这个矩阵化为 (1)当r=m时,α1,α2,…,αm线性无关.(2)当r 〔1〕高宇.矩阵初等变换的应用[J].高师理科学刊,2013(1):29-29. 〔2〕梁萌.矩阵初等变换的应用[J].河南科技,2013(3):187-187,199. 〔3〕戴立辉.线性代数[M].上海:同济大学出版社,2007. 〔4〕北京大学数学系.高等代数(第三版)[M].北京:高等教育出版社,2003. 〔5〕黄益生.高等代数[M].北京:清华大学出版社,2014.2. 〔6〕庄瓦金.高等代数教材[M].北京:科学出版社,2013.4. O151 A 1673-260X(2016)11-0013-02 2016-06-10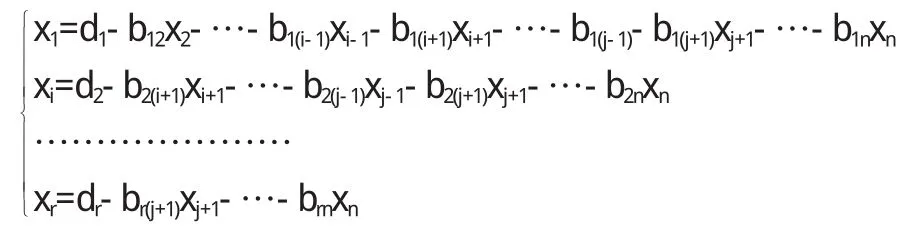
5 矩阵初等变换在二次型中的应用
6 矩阵初等变换在向量空间Pn中的应用





