立体几何中的动态问题

◇ 河南 颜如欣

立体几何中的动态问题

◇ 河南 颜如欣

立体几何中的动态问题,常规的处理方法是将立体问题转化为平面问题,再利用平面几何的相关知识求解,而翻折是连接平面几何与立体几何的纽带,实现平面向空间的转化.

1 动点轨迹问题

例1 若三棱锥A-BCD的侧面△ABC内一动点P到底面BCD的距离与到棱AB的距离相等,则动点P的轨迹与△ABC组成图形可能是( ).

如图1,过P作面BCD的垂线,垂足为O.在△ABC内过P作PE⊥AB,垂足为E,PF⊥BC,垂足为F.连OF,根据题意PE＝PO,在Rt△POF中,∠PFO为定值,所以

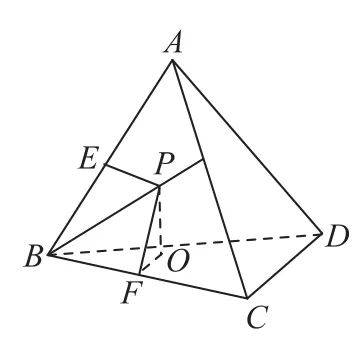
图1

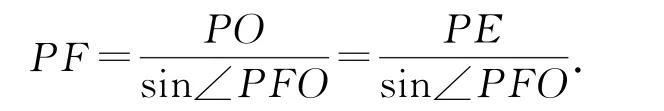
在平面中,动点到一个角的两边距离之比为常数,则动点轨迹为直线,结合sin∠PFO＜1,故PF＞PE,因此点P的轨迹与AC的交点AC在中点以上(靠近A方向),故选D.

本题打破平时以正方体为载体,采用四面体进行设计,作了一定的改进,难度较大.主要是将空间问题(点到面的距离)转化为平面上的问题处理.

2 面积问题

例2 如图2,长方体ABCD-A1B1C1D1中,已知AB＝AD＝2,AA1＝3,棱AD在平面α内,则长方体在平面α内的射影所构成的图形面积的取值范围是________.

图2

四边形ABCD和ADD1A1的面积分别为4和6,长方体在平面α内的射影可由这2个四边形在平面α内的射影组合而成.设面积为S,显然Smin＝4.若记平面ABCD与平面α所成的角为θ,则平面ADDA与平面α所成角为

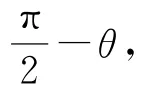
本题通过设出长方体侧面与平面α的夹角θ确定射影的面积,将射影面积表示为角θ的函数,利用三角函数最值求解方法确定射影面积的范围.将立体几何中的动态问题转化为函数问题来解决是常用思路.

3 距离或长度问题

例3 如图3所示,球O为边长为4的正方体ABCD-A1B1C1D的内切球,P为球O的球面上动点,M为B1C1中点,DP⊥BM,则点P的轨迹周长为________.

图3

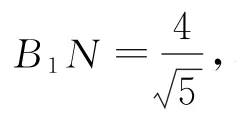
图4

图5

利用空间垂直关系的传递性可得线面垂直及线线垂直,从而确定动点轨迹,将空间问题转化为平面问题,由平面几何知识求得轨迹圆的半径从而得解.

4 位置关系判定问题

例4 在矩形ABCD中,AB＝2AD,E为边AB的中点,将△ADE沿直线DE翻折成△A1DE.若M为线段A1C的中点,则在△ADE翻折过程中,下面4个命题中正确的是________.

ABM是定值.

B点M在某个球面上运动.

C存在某个位置,使DE⊥A1C.

D存在某个位置,使MB∥平面A1DE.

如图6所示,取CD中点F,连接MF、BF,

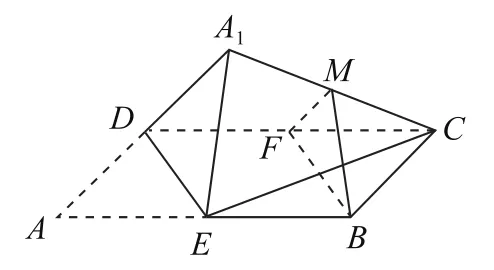
图6

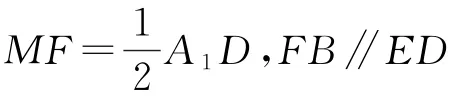
折叠问题是常见的动态问题,在折叠过程中,同一平面内的线面位置关系不变.

(作者单位:河南洛阳理工学院附属中学)