立体几何最值问题的拓展探究

◇ 江苏 刘 震 梁 兵

立体几何最值问题的拓展探究

◇ 江苏 刘 震 梁 兵

立体几何中的最值问题是高考常考题型,其中体积最值问题又是重中之重.此类试题的命制通常以定理及其基本图式为基础、空间想象能力为依托、位置关系转化为基本思维模式,通过构造函数求最值.下面引例说明.

例 在棱长为1的正方体ABCD-A1B1C1D1中,P1、P2分别是线段AB、BD1(不包括端点)上的动点,且线段P1P2∥平面A1ADD1,则四面体P1P2AB1的体积的最大值是( ).

本题以正方体为背景,线线、线面平行为依托,体积最值的求解为目标,意在考查同学们对空间图形的识别、应用能力.解答本题的基本策略:空间问题平面化、函数思想、化归转化等综合应用.

1 提取信息,理顺关系

信息1:如图1,已知P1、P2分别是线段AB、 BD1(不包括端点)上的动点且线段P1P2∥平面A1ADD1,由线面平行的性质可知P1P2∥AD1.

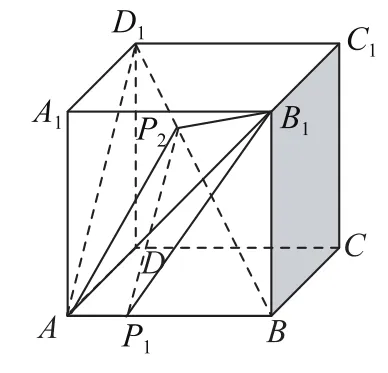
图1

信息2:所求四面体P1P2AB1的体积的最大值,即为三棱锥B1-P1P2A体积的最大值,而此三棱锥的高为点B1到面P1P2A的距离,即为点B1到面ABD1的距离,此距离为定值,故体积最值问题即为底面△P1P2A面积的最值问题.

2 空间化平面,探究最值

欲求△P1P2A面积的最大值,可将△ABD1从立体几何图形中提取出来,如图2所示,由已知可得AB⊥AD1,点P2的BD1上运动,随着P2位置的改变,△P1P2A的面积随之改变,因此将问题转化为运动过程中求△P1P2A面积的最值.

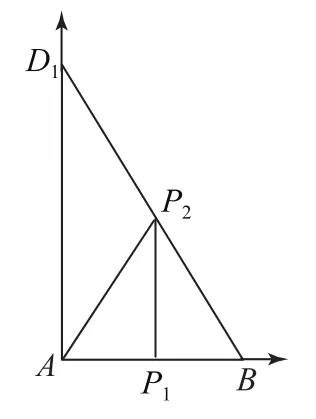
图2

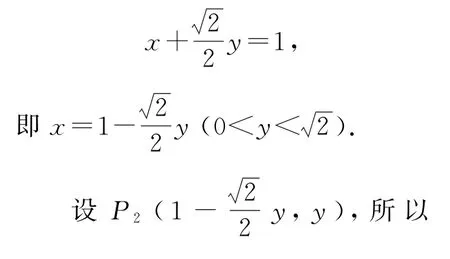
3 等价转化,探究空间距离

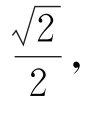
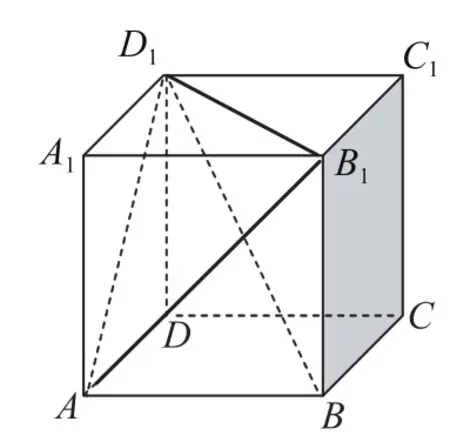
图3

转换视角,以A为顶点,则三棱锥A-BB1D1的底面的面积为高为点A1到直线B1D1的距离所以三棱锥A-BB1D1的体积

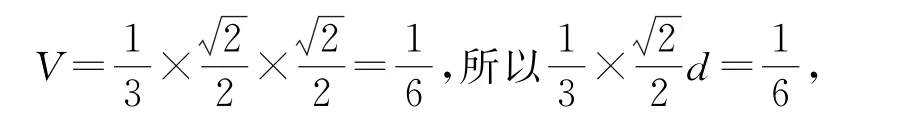
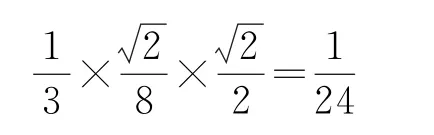
即为所求.综上可知正确选项为A.

解决立体几何中的最值问题不仅要具备较强的空间想象能力,而且还要会灵活运用代数、几何、三角等相关知识.此类问题既富思考情趣,又融众多知识和技巧于一体,综合性强、灵活性高、难度较大.充分体现了变知识立意为能力立意、在知识网络交汇点处设计试题能力的高考命题指导思想,是考查考生数学能力和数学素养的极好素材,应引起我们足够的重视.

(作者单位:江苏扬州市广陵区红桥高级中学)