古典概型及程序模拟在“清墩”牌型算法中的应用
2016-12-19刘佳乐刘志松徐优红
刘佳乐,刘志松,徐优红
(浙江海洋大学数学系,浙江舟山316022)
古典概型及程序模拟在“清墩”牌型算法中的应用
刘佳乐,刘志松,徐优红
(浙江海洋大学数学系,浙江舟山316022)
清墩是起源于舟山的一种扑克游戏,是地方特色文化的组成部分,但是到目前为止部分游戏规则尚不完善.本文以舟山清墩作为研究对象,先使用数学理论计算部分牌型的先验概率,再通过电脑程序模拟(以C-Free5来实现)统计后验概率,通过对比先验概率和后验概率最终确定该牌型出现的概率值.根据牌型出现概率大小判定牌型的大小,以完善清墩游戏规则,促进地方文化的发扬广大.
清墩; 概率; 程序模拟; 先验概率; 后验概率
1 引 言
清墩是一种具有鲜明舟山特色的扑克游戏[1],渔民苦于海上作业,发明了此游戏以聊解寂寞.初步探究约八十年代末期始流行于浙江省舟山市岱山县长涂镇,九十年代中期开始在浙江省舟山市各地风行,目前已成为舟山各大机构职工活动的一项重要娱乐项目.清墩游戏使用三副扑克,由于出牌规则相对简单,牌的组合方式非常灵活多样.正因如此,导致其牌型概率算法非常复杂,本文以计算清墩扑克游戏中炸弹(炸弹指的是同点数牌的张数≥4的牌型,此处暂且记它为4线炸;类似可定义5线炸,…)出现的概率为例,在不影响概率关系的前提下简化模型,将概率空间由四个玩家手中所持牌缩小为单个玩家手中手中所持牌,先用古典概型的理论方法计算其出现的先验概率,再利用计算机程序模拟的统计方法验证牌型出现的后验概率,通过对照修正,得到该牌型出现的概率值.
2 理论计算
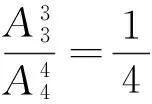
在具体牌型出现的概率计算中,由于游戏中使用三副扑克,且牌型组合非常自由,给概率计算带来很大困难. 为此我们首先将各种牌型的模型进行简化,利用概率加法公式对其进行拆分细化[2],然后充分借用概率论知识中的多种方法及其变形公式,以及一定的运算技巧,得到理论计算值.
为了表示方便,我们记牌大小A,2,3,…,K为炸弹的事件分别为B1,B2,…,B13,则由概率的加法公式[3]可以知道出现炸弹的概率:
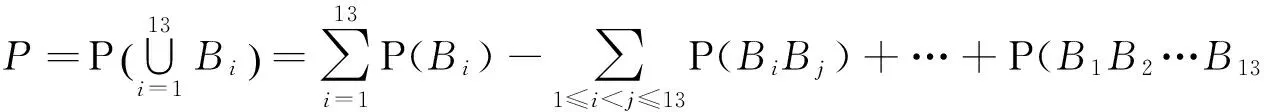
考虑到每个人摸到的牌数量不一样,在此我们主要研究了摸到牌的数量为40张的情形,对于摸到41张牌的情况可同样处理.因Bi可能性太多,考虑其对立事件,即i点数的牌摸到了0张,1张,2张,3张,故
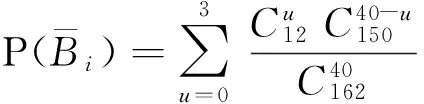
因为事件Bi和Bj(i,j=1,2…,13i≠j)有相同的概率分布,所以
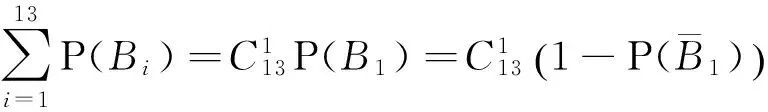
同理

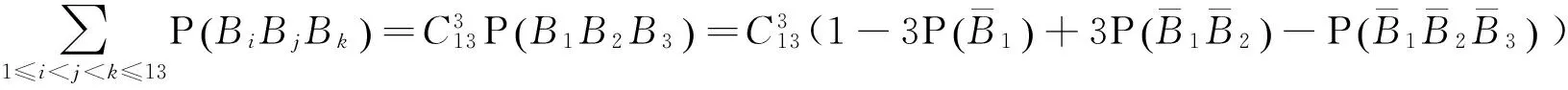
… …
并且注意到P(B1B2…B11)及后两项均不可能发生(因牌量总共40张,此处若发生,牌量必大于等于44张),故由上面的计算可以得到
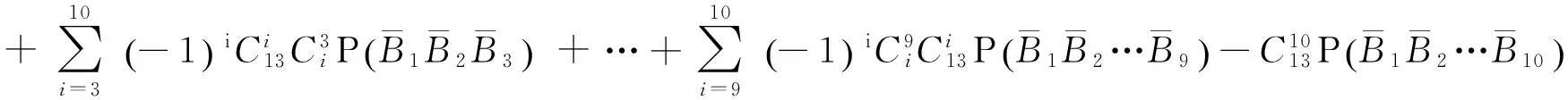

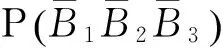
# include
double com(int m,int n)∥m中取n个
{
double i,j,sum=1;
for (i=m,j=0;j { sum=sum*i/(j+1); } return sum; } int main() { double a,b,c,sum=0; for(a=0;a<=3;a++) {for(b=0;b<=3;b++) { for(c=0;c<=3;c++) sum=sum+com(12,a)*com(12,b)*com(12,c)*com(162-12*3,40-a-b-c)/com(162,40); } } printf("%20.15lf",sum); return 0; } 注意:此处限于篇幅,未能把程序一一列出.事实上,在真正计算过程中,为了使结果更加准确,程序计算结果应该一次性实现,而不应该像上面那样分开计算每一项再求和.通过整个计算的过程,得到的最终结果P为0.999991748944871 . 此处利用计算机程序编程模拟[4]得到出现炸弹的概率,以便进一步检验我们理论计算的结果. #include #include #include #include #define TOTALNUM 162 #define DECKOFCARDS 54 enum POKER_SUIT{ CLUB, ∥梅花 DIAMOND, ∥方块 HEART, ∥红桃 SPADE, ∥黑桃 BLACK_JOKER, ∥小王 RED_JOKER ∥大王 }; struct Poker { int point; POKER_SUIT suit; }; ∥初始化一副牌 void InitOneDeckOfCards(Poker pokers[DECKOFCARDS]) { int size = 13; ∥每种花色13张 int i; ∥将每种花色依次放进一副牌 for(i = 0; i < size; i++) { pokers[i].point = i+1; pokers[i].suit = CLUB; } for( ; i < 2 * size; i++) { pokers[i].point = i % size+1; pokers[i].suit = DIAMOND; } for( ; i < 3 * size; i++) { pokers[i].point = i % size + 1; pokers[i].suit = HEART; } for( ; i < 4 * size; i++) { pokers[i].point = i % size + 1; pokers[i].suit = SPADE; } ∥把大小王放在一副牌的最后两张 pokers[52].point = 14; pokers[52].suit = BLACK_JOKER; pokers[53].point = 15; pokers[53].suit = RED_JOKER; } ∥随机打乱162张牌的顺序,模拟洗牌过程 void ShuffleCards(Poker pokers[TOTALNUM]) { 在 i-162中随机抽取一张放在第i个位置 for(int i = 0; i < TOTALNUM; i++) { int index = (rand() % (TOTALNUM - i)) + i; Poker p = pokers[index]; pokers[index] = pokers[i]; pokers[i] = p; } } ∥统计n张牌中是否有炸弹,有返回 1, 无返回 0 int HavaBomb(Poker pokers[], int n) { int result[15] = {0}; ∥存放每一个点数的牌的数量 for(int i = 0; i < n; i++) { int point = pokers[i].point; result[point-1] += 1; ∥point 存放在下标为point-1的位置上 if(result[point-1] >= 4) return 1; } return 0; } int main() { Poker p54Cards[DECKOFCARDS]; InitOneDeckOfCards(p54Cards); unsigned size = DECKOFCARDS * sizeof(Poker); Poker p162Cards[TOTALNUM]; memcpy(p162Cards, p54Cards, size); memcpy(&p162Cards[54], p54Cards, size); memcpy(&p162Cards[108], p54Cards, size); srand((unsigned)time(0)); int t = 0, bomb = 0, totalTime = 1000000000; double Prob; while(t++ < totalTime) { ShuffleCards(p162Cards); if(HavaBomb(p162Cards, 40) == 1) bomb++; } Prob=bomb/totalTime; printf("测试次数: %d, 有炸弹次数: %d
", totalTime, bomb); printf("Prob=%20.15lf",Prob); getchar(); return 0; } 运行结果(即出现炸弹的概率)为0.999991848000000 . 注意:此代码对计算扑克牌中其他牌型的概率也适用,只需在相应的地方适当修改即可. 一方面,通过对比理论计算和程序模拟得到的结果,不难发现这两处计算得到的结果相当吻合,误差仅为10-7,也可以进一步加大模拟次数使结果更加精准;另一方面,我们发现不出现四线炸的概率极小,也正是因为这种小概率事件的发生更加反映出我们计算结果的准确性. 首先,本文从理论出发,用实践检验理论[5],充分调动学生的主观能动性,加强学生动手动脑的能力,让学生把书读好读活;其次,清墩游戏深受舟山居民喜爱,是居民饭后茶余主要的休闲娱乐方式之一,也是舟山文化的一张名片,本文以此为背景引入课题,将数学的理论计算,计算机的程序模拟与文化的保护与传承相结合,这是本文的一大特色;最后,我们计划在之后的研究中进一步计算清墩中所有牌型的概率,从而完善游戏规则. [1] 张同宽. 舟山清墩运动研究[J]. 体育文化导刊,2011(5):32-35. [2] 陈维.概率论中事件的分割思想及其应用[J]. 大学数学,2011,27(2):159-161. [3] 茆师松,程依明,濮小龙.概率论与数理统计教程[M].2版.北京:高等教育出版社,2011:32-36. [4] 曹一鸣. 基于蒙特卡罗树搜索的计算机扑克程序[D]. 北京邮电大学硕士论文,2014. [5] 沙秀艳,辛杰.《概率论与数理统计》教学实践与探索[J].大学数学,2013,29(4):9-12. Classical Probability Calculation and Simulation Program Used in the "Qingdun" Poker Type Algorithm LIUJia-le,LIUZhi-song,XUYou-hong (Department of Mathematics, Zhejiang Ocean University, Zhoushan, Zhejiang 316022, China) Qingdun is a kind of Poker game originated from Zhoushan city, Zhejiang province, It’s a component of local distinctive culture. But some rules of the game is still incomplete. In this paper, we mainly research probability of some card type. Theoretical method will be used to calculate the prior probability firstly, and then we use computer programs based on C-Free5 to simulate the game and statistics the posterior probability. Contrast the prior probability and posterior probability and modification some procedure until we obtain the precise probability of some card type. Qingdun; probability ; simulate; prior probability ; posterior probability 2016-03-01; [修改日期]2016-06-07 浙江省自然科学基金项目(LQ12A01007);浙江省高等教育课堂教学改革研究项目(Kg2013197) 刘佳乐(1994-)男,本科在读,应用数学专业.Email:434870031@qq.com. O211; O242 C 1672-1454(2016)05-0088-043 计算机程序模拟计算
4 总 结
