Hom-李超三系的广义导子

周金森，范广哲

(1.龙岩学院信息工程学院，福建龙岩364012； 2.同济大学数学系，上海200092)



Hom-李超三系的广义导子

周金森1，范广哲2

(1.龙岩学院信息工程学院，福建龙岩364012； 2.同济大学数学系，上海200092)

首先回忆与保积Hom-李超三系相关的概念，并且给出它的广义导子、拟导子、中心导子、型心和拟型心的定义. 进一步地，研究这些导子之间的性质和联系.

保积Hom-李超三系； 广义导子； 拟导子； 型心； 拟型心

1 引 言

众所周知, 李三系最初源于对称空间的研究. 李三系作为一种代数系统, 与其它诸多代数体系有着密切的联系, 它的结构理论和表示理论已被广泛研究[1]. 保积Hom-李超三系是李三系的重要推广. 然而到目前为止, 对保积Hom-李三系的研究还是非常少.

导子和广义导子[2-10]在李理论的发展过程中起着非常重要的作用. 本文主要研究了保积Hom-李超三系的广义导子, 拟导子, 中心导子, 型心和拟型心的性质, 并且研究了它们之间的联系.

本文的主要结论归结为定理1, 2, 3, 4.

2 预备知识

首先来回忆一些与李三系, 保积Hom-李三系, 李超三系以及保积Hom-李超三系相关的概念和定义.

定义1 李三系是一个二元组(T,[·,·,·]), 其中T是域F上的线性空间, 三线性映射[·,·,·]：T×T×T→T,满足：∀x,y,z,u,v∈T, 有

[x,x,z]=0,

[x,y,z]+[y,z,x]+[z,x,y]=0,

[x,y,[z,u,v]]=[[x,y,z],u,v]+[z,[x,y,u],v]+[z,u,[x,y,v]].

定义2 保积Hom-李三系是一个三元组(T,[·,·,·],α), 其中T是域F上的线性空间, 三线性映射[·,·,·]：T×T×T→T, 线性映射α：T→T,满足∀x,y,z,u,v∈T, 有

α([x,y,z])=[α(x),α(y),α(z)],

[x,x,z]=0,

[x,y,z]+[y,z,x]+[z,x,y]=0,

[α(x),α(y),[z,u,v]]=[[x,y,z],α(u),α(v)]+[α(z),[x,y,u],α(v)]+[α(z),α(u),[x,y,v]].

设V,W是两个Z2-阶化线性空间, 线性映射f∶V→W称为ξ次(ξ∈Z2), 如果对于∀x∈Vγ, 都有f(x)∈Vγ+ξ. 所有这些映射的全体记为Hom(V,W)ξ, 它是Hom(V,W)的子空间. 进一步,f是0次, 即f(Vγ)⊆Wγ, 则称f是偶的.

[Ti,Tj,Tk]⊆Ti+j+k, ∀i,j,k∈Z2,

[x,y,z]=-(-1)xy[y,x,z],

(-1)xz[x,y,z]+(-1)yx[y,z,x]+(-1)zy[z,x,y]=0,

[x,y,[z,u,v]]=[[x,y,z],u,v]+(-1)(x+y)z[z,[x,y,u],v]+(-1)(x+y)(z+u)[z,u,[x,y,v]].

[Ti,Tj,Tk]⊆Ti+j+k, i,j,k∈Z2,

α([x,y,z])=[α(x),α(y),α(z)],

[x,y,z]=-(-1)xy[y,x,z],

(-1)xz[x,y,z]+(-1)yx[y,z,x]+(-1)zy[z,x,y]=0,

[α(x),α(y),[z,u,v]]= [[x,y,z],α(u),α(v)]+(-1)(x+y)z[α(z),[x,y,u],α(v)]

+(-1)(x+y)(z+u)[α(z),α(u),[x,y,v]].

注 如果(T,[·,·,·],α)是保积Hom-李超三系, 当取α=idT时, 此时(T,[·,·,·],α)变成了一个李超三系. 由此可知, 保积Hom-李超三系是李超三系的进一步推广.

下面给出保积Hom-李超三系T的各类导子和型心的概念.

[Dξ,Dη]=DξDη-(-1)ξηDηDξ.

证 直接计算易知.

定义5 设T为保积的Hom-李超三系, D∈Plξ(T)称为T的ξ次αk-导子, 如果

[D,α]=0,

D([x,y,z])= [D(x),αk(y),αk(z)]+(-1)ξx[αk(x),D(y),αk(z)]

+(-1)ξ(x+y)[αk(x),αk(y),D(z)].

对于任意x,y,z∈hg(T).

Der(T)=⊕k≥0Derαk(T),

其中Derαk(T)是Z2-阶化的, 即

定义6 D∈Plξ(T)称为T的ξ次αk-广义导子, 如果存在D′,D″,D‴∈Plξ(T)，使得

[D,α]=[D′,α]=[D″,α]=[D‴,α]=0,

D‴([x,y]) =[D(x),αk(y),αk(z)]+(-1)ξx[αk(x),D′(y),αk(z)]

+(-1)ξ(x+y)[αk(x),αk(y),D″(z)],

对于任意x,y,z∈hg(T).

定义7 D∈Plξ(T)称为T的ξ次αk-拟导子, 如果存在D′∈Plξ(T)，使得

[D,α]=[D′,α]=0,

D′([x,y])=[D(x),αk(y),αk(z)]+(-1)ξx[αk(x),D(y),αk(z)]

+(-1)ξ(x+y)[αk(x),αk(y),D(z)],

对于任意x,y,z∈hg(T).

定义8 设T为保积的Hom-李超三系, 若D∈Plξ(T), 且满足

[D,α]=0,

D([x,y,z]) =[D(x),αk(y),αk(z)]=(-1)ξx[αk(x),D(y),αk(z)]

=(-1)ξ(x+y)[αk(x),αk(y),D(z)].

对于任意x,y,z∈hg(T), 则称D为T的ξ次αk-型心.

定义9 设T为保积的Hom-李超三系, 若D∈Plξ(T), 且满足

[D,α]=0,

[D(x),αk(y),αk(z)]=(-1)ξx[αk(x),D(y),αk(z)]=(-1)ξ(x+y)[αk(x),αk(y),D(z)].

对于任意x,y,z∈hg(T), 则称D为T的ξγαk-拟型心.

定义10 设T为保积的Hom-李超三系, 若D∈Plξ(T), 且满足

[D,α]=0,

D([x,y,z])=[D(x),αk(y),αk(z)]=0,

对于任意x,y,z∈hg(T), 则称D为T的ξ次αk-中心导子.

根据以上定义,可得如下结论

ZDer(T)⊆Der(T)⊆QDer(T)⊆GDer(T)⊆Pl(T).

下面给出Hom-李超代数的子代数、Hom-子代数、理想及Hom-理想的定义.

定义12 设(L,[·,·],α)是Hom-李超代数，M是L的子空间，如果[M,M]⊆M，则称M是L的子代数；如果[L,I]⊆I，则称I是L的理想.

定义13 设(L,[·,·],α)是Hom-李超代数，若M是L的子代数，还满足α(M)⊆M，则称M是L的Hom-李子代数; 若I是L的理想, 还满足α(I)⊆I, 则称I是L的Hom-理想.

3 各类导子和型心的性质

定理1 设T为保积的Hom-李超三系, 则

(i)GDer(T), QDer(T)和C(T)是Pl(T)的Hom-李超子代数；

(ii)ZDer(T)是Der(T)的Hom-理想.

=α(D‴1([x,y,z])-[αk(x),D′1(y),αk(z)]-[αk(x),αk(y),D″1(z)])

[D1D2(x),αk+s(y),αk+s(z)]

=D‴1([D2(x),αs(y),αs(z)])-(-1)ξ(η+x)[αk(D2(x)),D′1(αs(y)),αk+s(z)]

-(-1)ξ(η+x+y)[αk(D2(x)),αk+s(y),D″1(αs(z))]

=D‴1D‴2([x,y,z])-(-1)ηxD‴1([αs(x),D′2(y),αs(z)])

-(-1)η(x+y)D‴1([αs(x),αs(y),D″2(z)])-(-1)ξ(η+x)[αk(D2(x)),D′1(αs(y)),αk+s(z)]

-(-1)ξ(η+x+y)[αk(D2(x)),αk+s(y),D″1(αs(z))]

=D‴1D‴2([x,y,z])-(-1)ηx[D1(αs(x)),αk(D′2(y)),αk+s(z)]

-(-1)(ξ+η)x[αk+s(x),D′1D′2(y),αk+s(z)]-(-1)ηx+ξ(x+y+η)[αk+s(x),αk(D′2(y)),D″1(αs(z))]

-(-1)η(x+y)[D1(αs(x)),αk+s(y),αk(D″2(z))]

-(-1)η(x+y)+ξx[αk+s(x),D′1(αs(y)),αk(D″2(z))]

-(-1)(η+ξ)(x+y)[αk+s(x),αk+s(y),D″1D″2(z)]-(-1)ξ(η+x)[αk(D2(x)),D′1(αs(y)),αk+s(z)]

-(-1)ξ(η+x+y)[αk(D2(x)),αk+s(y),D″1(αs(z))].

类似地, 可得

[D2D1(x),αk+s(y),αk+s(z)]

=D‴2D‴1([x,y,z])-(-1)ξx[D2(αk(x)),αs(D′1(y)),αk+s(z)]

-(-1)(ξ+η)x[αk+s(x),D′2D′1(y),αk+s(z)]-(-1)η(x+y+ξ)+ξx[αk+s(x),αs(D′1(y)),D″2(αk(z))]

-(-1)ξ(x+y)[D2(αk(x)),αk+s(y),αs(D″1(z))]

-(-1)ηx+ξ(x+y)[αk+s(x),D′2(αk(y)),αs(D″1(z))]

-(-1)(η+ξ)(x+y)[αk+s(x),αk+s(y),D″2D″1(z)]-(-1)η(x+ξ)[αs(D1(x)),D′2(αk(y)),αk+s(z)]

-(-1)η(x+y+ξ)[αs(D1(x)),αk+s(y),D″2(αk(z))].

同时利用

Diα=αDi, D′iα=αD′i, D″iα=αD″i, D‴iα=αD‴i,[Dξ,Dη]=DξDη-(-1)ξηDηDξ,

可得

[[D1,D2](x),αk+s(y),αk+s(z)]

=[D‴1,D‴2]([x,y,z])-(-1)(ξ+η)x[αk+s(x),[D′1,D′2](y),αk+s(z)]

-(-1)(η+ξ)(x+y)[αk+s(x),αk+s(y),[D″1,D″2](z)],

即

[D‴1,D‴2]([x,y,z])= [[D1,D2](x),αk+s(y),αk+s(z)]+(-1)(ξ+η)x[αk+s(x),[D′1,D′2](y),αk+s(z)]

+(-1)(η+ξ)(x+y)[αk+s(x),αk+s(y),[D″1,D″2](z)].

同理, QDer(T)是Pl(T)的Hom-李超子代数.

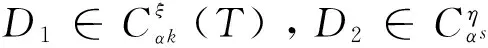
[[D1,D2](x),αk+s(y),αk+s(z)]

=[D1D2(x),αk+s(y),αk+s(z)]-(-1)ξη[D2D1(x),αk+s(y),αk+s(z)]

=D1([D2(x),αs(y),αs(z)])-(-1)ξηD2([D1(x),αk(y),αk(z)])

=D1D2([x,y,z])-(-1)ξηD2D1([x,y,z])=[D1,D2]([x,y,z]).

同理可证

(-1)(ξ+η)x[αk+s(x),[D1,D2](y),αk+s(z)]

=(-1)(ξ+η)(x+y)[αk+s(x),αk+s(y),[D1,D2](z)]=[D1,D2]([x,y,z]).

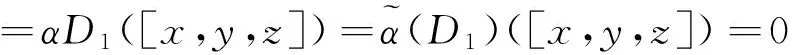
[D1,D2]([x,y,z])=D1D2([x,y,z])-(-1)ξηD2D1([x,y,z])

=D1([D2(x),αs(y),αs(z)]+(-1)ηx[αs(x),D2(y),αs(z)]

+(-1)η(x+y)[αs(x),αs(y),D2(z)])-0=0.

[[D1,D2](x),αk+s(y),αk+s(z)]

=[D1D2(x),αk+s(y),αk+s(z)]-(-1)ξη[D2D1(x),αk+s(y),αk+s(z)]

=0-(-1)ξηD2([D1(x),αk(y),αk(z)])+(-1)ξη[αs(D1(x)),D2(αk(y)),αk+s(z)]

+(-1)η(x+y)[αs(D1(x)),αk+s(y),D2(αk(z))]=0.

定理2 设(T,[·,·,·],α)保积Hom-李超三系, 则有如下结论

(i)[Der(T),C(T)]⊆C(T)；

(ii)[QDer(T),QC(T)]⊆QC(T)；

(iii)C(T)·Der(T)⊆Der(T)；

(iv)C(T)⊆QDer(T)；

(v)[QC(T),QC(T)]⊆QDer(T)；

(vi)QDer(T)+QC(T)⊆GDer(T).

[D1D2(x),αk+s(y),αk+s(z)]

=D1([D2(x),αs(y),αs(z)])-(-1)ξ(η+x)[αk(D2(x)),D1(αs(y)),αk+s(z)]

-(-1)ξ(η+x+y)[αk(D2(x)),αk+s(y),D1(αs(z))]

=D1D2([x,y,z])-(-1)ξη+(ξ+η)x[αk+s(x),D2D1(y),αk+s(z)]

-(-1)ξη+(ξ+η)(x+y)[αk+s(x),αk+s(y),D2D1(z)].

另一方面, 可得

[D2D1(x),αk+s(y),αk+s(z)]=D2([D1(x),αk(y),αk(z)])

=D2(D1([x,y,z])-(-1)ξx[αk(x),D1(y),αk(z)]-(-1)ξ(x+y)[αk(x),αk(y),D1(z)])

=D2D1([x,y,z])-(-1)(ξ+η)x[αk+s(x),D2D1(y),αk+s(z)]

-(-1)(ξ+η)(x+y)[αk+s(x),αk+s(y),D2D1(z)].

从而

[[D1,D2](x),αk+s(y),αk+s(z)]=[D1,D2]([x,y,z]).

类似可得

[[D1,D2](x),αk+s(y),αk+s(z)]=(-1)(ξ+η)x[αk+s(x),[D1,D2](y),αk+s(z)]

=(-1)(ξ+η)(x+y)[αk+s(x),αk+s(y),[D1,D2](z)]，

(ii) 同(i)的证明.

D1D2([x,y,z])

=D1([D2(x),αk(y),αk(z)]+(-1)ξx[αk(x),D2(y),αk(z)]

+(-1)ξ(x+y)[αk(x),αk(y),D2(z)])

=[D1D2(x),αk+s(y),αk+s(z)]+(-1)(ξ+η)x[αk+s(x),D1D2(y),αk+s(z)]

+(-1)(ξ+η)(x+y)[αk+s(x),αk+s(y),D1D2(z)].

[D(x),αk(y),αk(z)]

=(-1)ξx[αk(x),D(y),αk(z)]=(-1)ξ(x+y)[αk(x),αk(y),D(z)]=D([x,y,z]).

则

[D(x),αk(y),αk(z)]+(-1)ξx[αk(x),D(y),αk(z)]+(-1)ξ(x+y)[αk(x),αk(y),D(z)]

=3D([x,y,z]).

[[D1,D2](x),αk+s(y),αk+s(z)]+(-1)(ξ+η)x[αk+s(x),[D1,D2](y),αk+s(z)]

+(-1)(ξ+η)(x+y)[αk+s(x),αk+s(y),[D1,D2](z)]

=[D1D2(x),αk+s(y),αk+s(z)]+(-1)(ξ+η)x[αk+s(x),D1D2(y),αk+s(z)]

+(-1)(ξ+η)(x+y)[αk+s(x),αk+s(y),D1D2(z)]-(-1)ξη[D2D1(x),αk+s(y),αk+s(z)]

-(-1)ξη+(ξ+η)x[αk+s(x),D2D1(y),αk+s(z)]-(-1)ξη+(ξ+η)(x+y)[αk+s(x),αk+s(y),D2D1(z)].

由型心的定义, 可得

[D1D2(x),αk+s(y),αk+s(z)]=(-1)ξη+(ξ+η)x[αk+s(x),D2D1(y),αk+s(z)]，

[D1D2(x),αk+s(y),αk+s(z)]=(-1)ξη+(ξ+η)(x+y)[αk+s(x),αk+s(y),D2D1(z)]，

因此

[[D1,D2](x),αk+s(y),αk+s(z)]+(-1)(ξ+η)x[αk+s(x),[D1,D2](y),αk+s(z)]

+(-1)ξη+(ξ+η)(x+y)[αk+s(x),αk+s(y),[D1,D2](z)]=0.

(vi) 显然.

定理3 设(T,[·,·,·],α)保积Hom-李超三系, 则QC(T)+[QC(T),QC(T)]是GDer(T)的子代数.

证 由定理2(v),(vi)可得QC(T)+[QC(T),QC(T)]⊆GDer(T), 而且

[QC(T)+[QC(T),QC(T)],QC(T)+[QC(T),QC(T)]]

⊆[QC(T)+QDer(T),QC(T)+[QC(T),QC(T)]]

⊆[QC(T),QC(T)]+[QC(T),[QC(T),QC(T)]]+[QDer(T),QC(T)]

+[QDer(T),[QC(T),QC(T)]].

由阶化Hom-Jacobi恒等式易证

[QDer(T),[QC(T),QC(T)]]⊆[QC(T),QC(T)],

因此

[QC(T)+[QC(T),QC(T)],QC(T)+[QC(T),QC(T)]]

⊆QC(T)+[QC(T),QC(T)], 故QC(T)+[QC(T),QC(T)]

是GDer(T)的子代数.

定理4 设(T,[·,·,·],α)保积Hom-李超三系, α是满射,Z(T)是T的中心,则

[C(T),QC(T)]⊆Hom(T,Z(T)),

特别地, 若Z(T)=0, 则[C(T),QC(T)]=0.

[[D1,D2](x),y,z]=[[D1,D2](x),αk+s(y′),αk+s(z′)]

=[D1D2(x),αk+s(y′),αk+s(z′)]-(-1)ξη[D2D1(x),αk+s(y′),αk+s(z′)]

=D1([D2(x),αs(y′),αs(z′)])-(-1)ηx[αs(D1(x)),D2(αk(y′)),αk+s(z′)]

=D1([D2(x),αs(y′),αs(z′)])-(-1)ηx[D1(αs(x)),αk(D2(y′)),αk(αs(z′))]

=D1([D2(x),αs(y′),αs(z′)])-(-1)ηxD1([αs(x),D2(y′),αs(z′)])

=D1([D2(x),αs(y′),αs(z′)])-D1([D2(x),αs(y′),αs(z′)])=0.

因此[D1,D2](x)∈Z(T), 而且[D1,D2]∈Hom(T,Z(T)). 特别地, 若Z(T)=0, 则显然有[C(T),QC(T)]=0.

[1] Lister W. A structure theory of Lie triple systems[J]. Trans. Amer. Math. Soc., 1995,72:217-242.

[2] Ammar F, Makhlouf A. Hom-Lie superalgebras and Hom-Lie admissible superalgebras[J]. J. Algebra, 2010, 324(2):1513-1528.

[3] Chen L, Ma Y, Ni L. Generalized derivations of Lie color algebras[J]. Results. Mathematics, 2013,63:923-936.

[4] 周佳，牛艳君，陈良云. Hom-李代数的广义导子[J]. 数学学报，2015,58(4):551-558.

[5] Leger G F, Luks E M. Generalized derivations of Lie algebras[J]. J. Algebra, 2000,228(2):165-203.

[6] Yuan L. Hom-Lie color algebra structures[J]. Comm. Algebra, 2012,40:575-592.

[7] Zhang Q, Zhang Y. Derivations and extensions of Lie color algebra[J]. Acta Mathematica Scientia, 2008,28: 933-948.

[8] Zhang R, Zhang Y. Generalized derivations of Lie superalgebras[J]. Comm. Algebra, 2010,38:3737-3751.

[9] 巫永萍. 5维幂零李代数的导子代数的结构[J]. 大学数学, 2012,28(5):76-79.

[10] 法焕霞, 李军波, 程永胜.W-代数W(2,2)的单参数变量子形变[J]. 大学数学, 2013,29(2):29-32.

Generalized Derivations of Hom-Lie Supertriple Systems

ZHOUJin-sen1，FANGuang-zhe2

(1. School of Information Engineering, Longyan University，Fujian Longyan 364012, China;2. Department of Mathematics, Tongji University, Shanghai 200092,China)

Firstly we recall some concepts associated with multiplicative Hom-Lie supertriple Systems. Moreover, we give the definitions of the generalized derivations, quasiderivations, center derivations, centroids and quasicentroids. Furthermore, we investigate some properties and connection between these derivations.

multiplicative Hom-Lie supertriple systems; generalized derivations; quasiderivations; centroids; quasicentroids

2016-03-23；[修改日期]2016-04-15

国家自然科学基金(11431010)

周金森(1969-),男，硕士，副教授，从事李理论研究.Email:zjs9932@126.com.

范广哲(1989-),男，硕士，从事李理论研究.Email:yzfanguangzhe@126.com.

O152.5

A

1672-1454(2016)05-0018-07