关于《线性代数》中术语等标准化问题的探讨

肖 燏，黄爱武，孙桂秋

(湖南中医药大学数理教研室，长沙410208)



关于《线性代数》中术语等标准化问题的探讨

肖 燏，黄爱武，孙桂秋

(湖南中医药大学数理教研室，长沙410208)

基于国内各高等院校所使用的线性代数教材编写不规范、缺乏统一性和通用性的现状，收集了各种版本中出现的非标准实例，参照国内外数学史和国际通用标准，按术语、译名、符号、格式四类分类加以标准化.

标准化； 术语； 译名； 符号； 格式

教材是承载教学内容和信息的载体，教材的标准化体现了教学内容和信息的统一性、通用性、严谨性和传承性.虽然近几年对于教材标准化问题的探讨已有不少，但国内对于高等院校线性代数教材的标准化问题讨论极少，以致现在各版本的教材仍然编写很不规范，缺乏统一性和通用性[1-8].本文选用了当前各高校较常使用的教材版本，通过收集和对比，并参照国内外数学史和国际通用标准，按术语、译名、符号、格式的标准化来做详细地讨论.

1 术语的标准化

术语使用混乱是国内线性代数教材中一个很严重的问题.带有歧义的表述、词序的逻辑错误、过于简单化的外文直译和较为主观的概念定义，给教师讲授和学生理解带来很大的困难，亟待规范使用.以下就几个常见问题总结出来并加以标准化.

1.形与型

形和型，是线性代数的术语里，经常会出现的两个字，然而有部分教材在这两个字的使用上却并不规范.

形和型是有区别的：型，“筑器之法也”——《说文》.指类型、样式，是同类事物共同具有的特征；形，“象形也”——《说文》.指实体、样子、状况、表现等，是个体事物区别于其他事物的不同特征.

因此，在教材所涉及的术语中，规范的文字使用应该是：行阶梯形矩阵、矩阵的行最简形和标准形；二次型的规范形、标准形；矩阵同型.

2.线性齐次、非齐次方程组 / 齐次、非齐次线性方程组

方程(组)有线性和非线性的.在线性的前提下，我们把常数项为零的方程称为齐次的，常数项不为零的方程称为非齐次的.而在非线性方程里，齐次的含义和线性方程里齐次的含义不一样.比如二次齐次方程：x2-xy+2y2=0，此处的齐次是指同次.

多数教材在讲述线性方程组的时候，由常数项为零或不为零，将其分类定义为齐次线性方程组和非齐次线性方程组，这种表述显然在词序和意义上是逻辑错误的.

标准的定义陈述应该是，交代前提再分类.因此，当线性方程组常数项为零时，称为线性齐次方程组；当常数项不为零时，称为线性非齐次方程组.这种定义也与它们的英文表述一致：homogeneous system of linear equations(线性齐次方程组)，nonhomogeneous system of linear equations (线性非齐次方程组).

3.分块对角矩阵/对角分块矩阵

各教材都会对分块矩阵加以介绍，并讨论几种特殊的分块阵.而“对角分块矩阵”、“上(下)三角形分块矩阵”等名称在某些版本的教材中出现，如[4].这种定义既忽略了块矩阵的本质，也容易引起歧义.比如，对角分块矩阵，更容易让人误以为是对角阵，再进行分块操作.

标准术语应该先强调分块、再描述分块后的特点，结合简洁性，所以应该是：块对角阵、块三角阵等.常见的特殊分块阵英汉对照列举如下：

block diagonal matrix 块对角阵；block triangular matrix 块三角阵；block tri-diagonal matrix 块三对角阵；block diagonal sparse matrix 块对角稀疏阵；block bordered diagonal matrix 块对角加边阵；block diagonal similarity matrix 块对角相似度阵.

4.行阶梯阵、行最简阵、矩阵的标准形 / 矩阵的等价标准形、阶梯形矩阵、简化阶梯形矩阵

在矩阵的初等变换中，会出现如下两种矩阵：

在国外的文献中，我们见到的表述确实是matrixAin echelon form(阶梯形矩阵)和 matrixBin reduced echelon form(简化的阶梯形矩阵).有些版本的教材会照搬直译过来，而这种直译式术语造成了概念的模糊不清，只做到了翻译的“信”，却不“达”：(i)没有交代是行变换还是列变换；(ii)没有交代简化到何种程度.至于某些教材中给出的“等价标准形”，基于变换本身就是等价的，此为定义重复，不可取.

综上，标准的术语应为：行阶梯阵、行最简阵和矩阵的标准形.既点明了是行变换，又给出了变换后矩阵的确切形状.

5.向量组的极大无关组 / 最大无关组

英文表述maximal system of linear independence，或者maximal linearly independent subset，在各版本的教材中叫法不一，有的称为向量组的极大无关组，有的称为向量组的最大无关组.

在高等数学的教材中，我们明确区分过极值和最值：在问题所讨论的区域内，若最值存在必唯一，是一个整体概念；而极值可以有多个，是一个局部概念.同理，当我们在一个关于向量组的问题中需要考察个数最多的线性无关组时，因为向量组常被加以扩充或删减，这个“最多个数”在此问题中并非唯一.例如：

为了判定线性方程组Ax=β的解，需求出系数矩阵所对应的列向量组A:α1,α2,…,αn和增广矩阵所对应的列向量组B:α1,α2,…,αn,β的秩，显然，向量组A,B中个数最多的线性无关组不一定相同.因此，我们对这一概念的命名必须为向量组中向量的增删留有余地.

因此，标准的术语应为：向量组的极大无关组.

6.线性非齐次方程组Ax=β对应的线性齐次方程组/ 导出组Ax=0

英文表述derivedsystemoflinearequationsAx=β，有些教材称为导出组，有些称为对应的线性齐次方程组，还有些二者都加以引入.

显然，由方程组Ax=β得到方程组Ax=0，并不需要任何计算导出的过程，“导出组”表述晦涩，含义不明.而“对应的线性齐次方程组”则概念直观，清晰明了.

因此，标准的名称应首选为：对应的线性齐次方程组，导出组作为次选.

7.线性方程组的通解、全部解 / 一般解

当线性方程组有无穷多个解时，解的名称在各教材中是最混乱的.比如：

由线性方程组

解得

(1)

令x3=c，得方程组的解为

(2)

有教材将(1)定义为一般解而(2)为通解，通解=全部解；有教材将(2)定义为一般解，一般解=通解=全部解；也有教材略去一般解和通解的概念，直接将(2)定义为全部解.

一般解的概念不少版本的教材已不采纳，属于过时不常用的，应该废弃.通解在微分方程里是一直存在的概念，其特点是带有任意常数c(其个数和微分方程的阶数相同)；而(2)同样由任意常数c来表示，从数学概念的一致性来说，也应该被称为通解.虽然在微分方程里，通解≠全部解，而在线性方程里，通解=全部解，这正是由方程类别的不同而造成的，教师在讲授时理应加以甄别.

由此看来，(2)的标准名称应为通解.可在此定义上作进一步说明：在线性方程组里，求出了通解就求出了全部解.

8.唯一 / 惟一

这是讨论线性方程组的解的时候经常出现的术语：唯一(惟一)解.另外，在向量的线性组合里，也有关于“表达式唯一(惟一)”的阐述.

依据2011年发行的《现代汉语异形词规范词典》[9]，“唯一”视为规范词.因此在教材编写时，规范的文字使用是：

线性方程组的唯一解；表达式唯一等.

9.标准 / 规范

“标准”和“规范”在线性代数教材中被频繁引用，以给出某类代数名词、形式和操作的规范性参照.然而，对这二词的使用各教材却标准不一，这是不严谨的.比如，到底是作向量组的标准正交化还是规范正交化？二次型的标准形和规范形到底是何种形式？各版本教材应该有统一明确的解释.

事实上“标准”是比“规范”更严格的形式，具有形式最简性或唯一性.据此，相关标准术语列举如下：

向量组的标准正交化；向量空间的标准正交基；矩阵的标准形.特别指出二次型

经正交变换我们可将其化为只含有完全平方项

(3)

进一步化为系数只取1，-1或0

(4)

依据之前的命名标准，(3)应该叫做二次型的规范形，(4)应该叫做二次型的标准形.

10.基本单位向量组、标准单位向量组 / 单位向量组、单位坐标向量组、初始单位向量组

标题列举的名称均是各版本教材对向量组

给出的定义.

由于模为1的向量都称为单位向量，所以将其定义为单位坐标向量组或者单位向量组等都是不严谨的.基于它是生成n维向量空间的向量组中最基本的一组，从这一本质属性考虑，其标准称谓应该是基本单位向量组.而将标准单位向量组作为次选.

11.分拆/ 分解

分拆和分解含义不同，分拆是一种形式上的操作，分解是一种数学运算，二者不可混淆.比如：

λ2+3λ+2=(λ+1)(λ+2)，此为二次多项式的分解.

2 译名的标准化

依据《中华人民共和国国家通用语言文字法》之规定，教材作为文化载体，编写时理应使用规范文字.同时，各教材使用规范通用的外语译名也是非常重要的.比如，在线性代数课程里讲授的克拉默法则，在其它数学课程中以克莱姆法则出现时，学生常常不知所云.以下就教材中经常使用的外文译名，依据有影响的典籍和其它权威词典，并参考数学史中的习惯用法，加以标准化.另外，有些教材在介绍外文译名时没有中外对照给出，这一点也是不周全的.

1.Vandermonde determinant

教材中常见的译名有：范德蒙(范德蒙德、范得蒙)行列式.

规范的译名为：范德蒙(Vandermonde)行列式[10,14].范德蒙德是次选择法.不译成范得蒙.

2.Cramer’s rule

有的教材中翻译作：克拉默法则，实为不妥.文献[14]对此有专门的论述.克拉默是另外一位数学家，不可混淆.

规范的译名为：克莱姆(Cramer)法则[14].

3.Jordan canonical form

教材中常见的译名有：约旦(约当、约尔当、若当、若尔当、若尔丹)标准形.另外，现在的大众媒体通常将其翻译作“乔丹”.文献[11]中译为约当，可作为次选择法.第一个字译成“若”，则与原发音相差远矣.这一点的详细解释可参看文献[14]中的“颜森”条.

规范的译名为：约旦(Jordan)标准形[10].

4.Cauchy-Schwarz inequality

有时被译作：柯西—许瓦兹(施瓦兹)不等式.

规范的译名为：柯西—施瓦茨(Cauchy-Schwarz)不等式[12,13].

3 符号的标准化

线性代数教材中的符号使用，可以说是大学数学各门类教材中最杂乱、最让教师和学生无所适从的.这一节从各版本教材中总结出一些使用频率很高、但符号不标准的问题，逐一阐述并标准化.

1.行列式、矩阵的行列式符号

因为AA*=(detA)E，所以det(AA*)=det((detA)E)=(detA)ndetE=(detA)n，…

这样的运算式看得人眼花缭乱.所以标准的符号使用是很有必要的.列举如下：

2.转置行列式、转置矩阵的符号

转置行列式在教材里常被记作D′或DT，而转置矩阵相应地被记作A′或AT.

D′或A′的记号易与求导符号混淆，不可取.而由转置行列式和转置矩阵的英文名：transposed determinant & transposed matrix，取首字母大写则含义清晰，便于联想到原义.

因此，转置行列式应记作DT，转置矩阵应记作AT.

3.矩阵与矩阵相乘

矩阵Am×n乘以矩阵Bn×s，大多数教材记作C=AB，也有教材记作C=A·B. 后者显然是不对的.比如，当A，B都为1×n的行矩阵(n维行向量)时，此记号有歧义：可理解为矩阵与矩阵相乘，则运算不可行；亦可理解为向量的内积(点积)，此时运算可行.

因此，矩阵Am×n乘以矩阵Bn×s应记作C=AB.

4.单位矩阵

英文名identity matrix，常见的记号为E或者I. 按取首字母原则本应记作I，但I与数字1太形似，很容易混淆和误读，引起不必要的错误.因此，单位矩阵记作E. 这里的“E”可看作是“I”的修饰结果，正如空集符号“∅”是由“○”添加一斜线修饰而成一样.顺便说一下，空集符号不能用希腊字母“Φ”来表示.

5.初等矩阵

初等矩阵的符号可以说是一版教材一个记号，都是带有临时说明性和编者的部分主观性的.按初等对调、初等数乘、初等倍加列举几个版本：

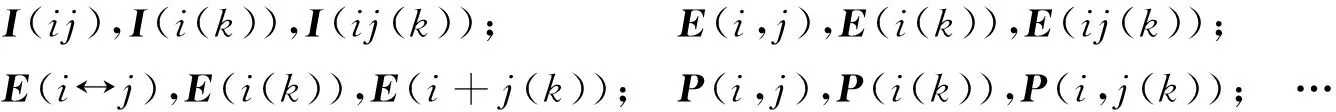
因为初等矩阵是由单位矩阵经过一次初等变换得到，所以前面的大写英文字母应该与单位矩阵的记号一致，即E；初等对调和初等数乘符号的争议性不大，取多数教材认可的版本.所以，初等对调矩阵和初等数乘矩阵的标准符号分别为E(i,j)，E(i(k)).

而初等倍加矩阵不可避免地行列读法不通用，规定符号时，读法上不能只体现行变换，如E(i+j(k))；也不能只乘不加，如E(i,j(k)). 所以，我们郑重地推荐下面的符号：

E(j+i,(k)). 其中，正读为行，表示：单位矩阵E经(ri+rj×k)的变换所得到的初等阵；逆读为列，表示：单位矩阵E经(cj+ci×k)的变换所得到的初等阵.该符号在包括求逆在内的一系列推导中明显具有优越性.

6.矩阵等价、矩阵相似、矩阵合同

矩阵A与B等价教材中常用的符号有：A≅B，A→B，A～B；矩阵A与B相似常用的符号为A～B(或无记号，文字描述)；矩阵A与B合同常用的符号为A≃B(或无记号，文字描述).

依据矩阵A与B等价的定义，是指A(本阵)能够通过有限次初等变换化成B(目的阵)，此处符号应取：A→B.

类同于几何里图形相似的记号，矩阵A与B相似的记号为：A～B.

矩阵A与B合同宜记作：A≃B.

7.向量的记号

向量在各教材中一般用小写加黑的希腊字母或英文字母来表示，如向量α，β，γ或向量a，b，c等，零向量用数字零加黑“0”来表示.而从多年的教学经验来看，字母或数字加黑是很考验眼力和手法的，不可取.希腊字母可直接用于表示向量，并不致引起混淆和歧义.而英文字母和数字零，用几何里的标准记法，加箭头表示向量.所以向量的标准记号是：

8.矩阵、向量组的秩

矩阵和向量组的秩有的教材中用r或R来表示.在数学分析与复变函数论里，当我们把一个函数首字母大写，或者对应取多值，如Arcsinx；或者对应在复数范围内取值，如Logax. 当矩阵的元素皆在实数范围内取值时，矩阵的秩rank若取首字母，则需小写.同时，基于求秩是一种运算，运算符应取正体.所以矩阵和向量组的秩应以正体小写的英文字母r来表示.即：矩阵A的秩记为r(A)，向量组α1α2…,αn的秩记为r(α1α2…,αn).

另一种写法就是写全rank，这也是线性代数论文中常见的写法.

9.向量的内积

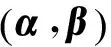
10.向量的模(长度)

(5)

只是范数的一种，称为欧氏范数或欧氏长度，直接将其定义为向量的范数，涵盖的范围太广.

所谓“定义”，是对于一种事物的本质特征或一个概念的内涵和外延所作的确切而简要的说明.简言之，定义不应越级.把“一个人走过来”说成“一个生物走过来”就是越级.所以，(5)式标准的名称应该是：向量的模，或者长度.范数的符号“‖·‖”不应取，因此向量α的模记作：|α|.

11.向量正交(垂直)

这是同一个概念在不同维数空间中的不同说法.在不超过3维时，常用“垂直”这个词，在3维以上时，就用“正交”这个词了.空间解析几何里通常称为向量垂直，线性代数中通常称为向量正交.从标准性表述来说，“正交”是规范的数学用语，而“垂直”是通俗的名词，可作为对“正交”的通俗解释.因此，在编写线性代数教材和教师授课时，我们应以正交为首选概念.

在各版本的教材中，只有使用了“垂直”这一概念的，才会引入记号“⊥”. 正确直观的符号可以简洁数学语言和推导，基于以上的讨论，向量正交应给以记号“⊥”. 即，向量α与β正交，记作α⊥β.

4 格式的标准化

1.矩阵的初等变换

由第3节6.中对于矩阵等价符号的讨论，作矩阵初等变换时，变换前矩阵和变换后矩阵之间的标准衔接格式是：→.

2.行列式和矩阵的变换步骤

当我们在计算行列式，或者对矩阵作初等变换时，在推算过程中要求写出具体步骤.而各教材的步骤格式五花八门，标准不一.比如：

r1+r2+r3+r4或r1+(r2+r3+r4).

标准的格式列举如下(以行为例)：

对调第i行和第j行：ri↔rj；将第i行乘以非零常数k：ri×k；将第j行乘以非零常数k加到第i行：ri+rj×k. 特别指出，在此种情形里，若把第2，3，4行同时加到第1行，标准的格式应为：r1+r2,r3,r4. 这种格式才能清楚地表出被加行，即变化的到底是哪一行.

3.线性方程组的解

不少教材在求n元线性方程组时，其解的格式是x1= ,x2= , …,xn= . 这种格式在逻辑关系上是错误的，没有表示出n个结论须同时成立.

标准的格式应为

4.不等式的表示

[1] Lee W. Johnson等.Introduction to Linear Algebra[M].5版.北京：机械工业出版社，2002.

[2] 同济大学数学系.工程数学：线性代数[M].6版.北京：高等教育出版社，2013.

[3] 邱森.线性代数[M].2版.武汉：武汉大学出版社，2013.

[4] 赵树嫄.线性代数[M].4版.北京：中国人民大学出版社，2013.

[5] 王尚平，李艳丽.线性代数[M].2版.北京：机械工业出版社，2006.

[6] 高宗升，周梦，李红裔.线性代数[M].2版.北京：北京航空航天大学出版社，2009.

[7] 许彪，谢巍，兰恒友.线性代数[M].成都：西南交通大学出版社，2012.

[8] 徐爱华.线性代数[M].上海：同济大学出版社，2015.

[9] 李行健.现代汉语异形词规范词典[M].2版.上海：上海辞书出版社，2011.

[10] 武汉大学数学系数学专业.线性代数[M].北京：人民教育出版社，1977.

[11] 卡兹V J.数学史通论[M].2版.李文林，等译.北京：高等教育出版社，2004：507-547.

[12] 张鸿林.英汉数学词汇[M].2版.北京：清华大学出版社，2010.

[13] 王有志.汉英数学词汇[M].北京：清华大学出版社，2008.

[14] 孙桂秋.数学、物理学中人名译名的标准化[J].中国科技翻译，2013(1)：15-18.

The Discussion on the Standardization of Terminology in Linear Algebra

XIAOYu,HUANGAi-wu,SUNGui-qiu

(Department of Mathematics and Physics, Hunan Traditional Chinese Medicine University, Changsha 410208，China)

Based on the actualities that the domestic textbooks of linear algebra are compiled non-standardly and absent of uniformity and universality, we collect nonstandard examples in kinds of versions, and referring to the history of mathematics and to the international universal standard, discuss in detail the standardization of terminology, translated name, symbol and format.

standardization; terminology; translated name; symbol; format

2016-04-08； [修改日期]2016-05-22

肖燏(1974-)，女，硕士，讲师，从事线性代数研究. Email:2649237123@qq.com

O151.2

C

1672-1454(2016)05-0054-07