粒子群优化结构测量矩阵的遥感压缩成像
2016-12-19陶会锋凌永顺殷松峰
陶会锋,杨 星,陈 杰,凌永顺,殷松峰
(1.电子工程学院 脉冲功率激光技术国家重点实验室,安徽 合肥 230037;2.电子工程学院 红外与低温等离子体安徽省重点实验室,安徽 合肥 230037;3. 安徽建筑大学 电子与信息工程学院,安徽 合肥 230601)
粒子群优化结构测量矩阵的遥感压缩成像
陶会锋1,2*,杨 星1,2,陈 杰3,凌永顺1,2,殷松峰1,2
(1.电子工程学院 脉冲功率激光技术国家重点实验室,安徽 合肥 230037;2.电子工程学院 红外与低温等离子体安徽省重点实验室,安徽 合肥 230037;3. 安徽建筑大学 电子与信息工程学院,安徽 合肥 230601)
针对块循环测量矩阵应用于遥感压缩成像存在图像重构性能不理想的问题,本文把粒子群智能优化算法引入到块循环矩阵优化中,实现了在保持矩阵结构不变的同时对块循环矩阵的优化。首先以相关系数的Welch界为阈值约束Gram矩阵非对角元素构造目标矩阵;然后以Gram矩阵逼近目标矩阵的方式建立目标函数,将优化对象改为构造块循环矩阵的自由元向量。为提高优化效率,文中采用权重自适应更新的方式提高粒子搜索能力。开展了相关重构对比实验,结果表明,优化后的块循环测量矩阵在保持矩阵结构的同时,降低了与稀疏变换矩阵的相关性,其与稀疏变换矩阵的最大相关系数、平均相关系数和阈值平均相关系数分别降低了0.027 3、0.017 5和0.004 6,得到的结果显示优化的块循环矩阵提高了图像的重构性能。
遥感图像;压缩成像;图像重构;块循环矩阵;粒子群优化
1 引 言
信息时代,随着信息需求量的与日俱增,高空间、时间和光谱分辨率的图像获取成为遥感成像的重要发展趋势。由于成像系统硬件的限制和数据传输、处理的压力,基于Nyquist采样定理的信息获取方式用于高分辨率遥感成像系统时存在难以突破的瓶颈[1-2]。压缩感知(Compressive Sensing, CS)理论[3]的提出为遥感信息获取提供了新的解决方案。基于CS理论的压缩成像技术通过对光参量进行调制,能以较少数据采样量恢复出高分辨率图像,实现采样、压缩和数据处理一体化。通过选用不同光调制器件,目前已发展了多种压缩成像系统和模型,如单像素相机[4]、偏振光压缩成像[5]、压缩编码孔径成像[6]以及高光谱压缩成像[7]等。
测量矩阵是CS理论的核心,其能否在保证图像重构性能的同时兼顾实时性一直是制约CS理论走向实用化的重要因素。高斯随机矩阵能够以较大概率满足有限等距性质(Restricted Isometry Property, RIP)[8],其作为测量矩阵具有很强的普适性。但是高斯随机矩阵中自由元素太多,不利于硬件实现,同时其存储要求高和计算复杂,并不适合应用于实际遥感压缩成像。Marcia等根据压缩编码孔径的成像机理,提出将易于硬件实现的块循环矩阵(Block Circulant Matrix)[5]作为测量矩阵,但块循环测量矩阵的重构性能还不理想。为缓解这一矛盾,一种有效的措施是对块循环测量矩阵进行优化,降低其与稀疏变化矩阵的相关性。
针对随机测量矩阵的优化问题,国内外学者已提出很多相关算法:如Elad将Gram矩阵中非对角元素线性收缩至限定阈值[9];Abolghasemi等提出的等角紧框(Equiangular Tight Frame, ETF)方法[10]; Zheng等提出基于拟牛顿法的优化方法[11]等。这些方法主要是基于Gram矩阵的确定性迭代优化,计算过程相对繁琐,同时需要优化问题满足严格的数学性质(如连续、可导),从而限制了优化对象的选择。这些方法用于具有特定结构的块循环矩阵优化时,容易破坏矩阵结构,从而影响其实用性能。基于此,本文把粒子群智能优化(Particle Swarm Optimization, PSO)算法引入到块循环矩阵优化中,而优化对象则变为构造矩阵的自由元向量,以Welch界为阈值约束Gram矩阵非对角元素来构造目标矩阵,以Gram矩阵逼近目标矩阵的方式建立目标函数。为提高优化效率,文中采用权重自适应更新的方式提高粒子搜索能力。通过实验验证了优化测量矩阵的重构性能。
2 遥感压缩成像块循环测量矩阵编码
遥感压缩成像是通过在光学系统中添加光调制器件(如数字微镜元件(Digital Micromirror Device,DMD),编码孔径(Coded Aperture)和空间光调制器等)对光参量进行调制以实现压缩采样。其结构示意图如图1所示。
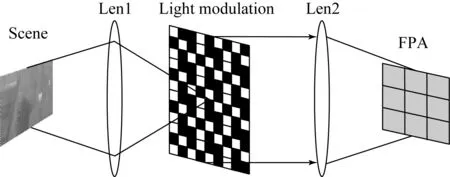
图1 遥感压缩成像示意图
设光调制器的点扩散函数为h,则场景X的编码模型为:
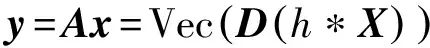
(1)
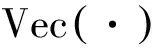
可通过傅里叶变化将式(1)中卷积运算转换到频域运算:

(2)
式中:Γ=F⊗F,表示离散傅里叶变换矩阵Kronecker积;CH是对角元素为ΓH的对角矩阵。此时:
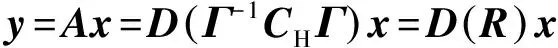
(3)
如果忽略下采样矩阵的影响,由式(3)可知,压缩成像的测量矩阵:
A=Γ-1CHΓ.
(4)
由于Γ具有对角化循环结构,由矩阵运算可知A具有块循环结构。文献[12-13]指出块循环矩阵能够以一定概率满足RIP,本文用于指导光调制器的设计,从而实现光参量编码。其数学形式:

(5)

(6)

3 基于粒子群的块循环测量矩阵优化
对块循环测量矩阵优化是提高其图像重构性能的一种有效措施,针对现有测量矩阵优化方法容易破坏矩阵结构的问题,本文提出了利用PSO智能算法对块循环测量矩阵进行优化。
3.1 测量矩阵优化的目标函数
文献[9]指出通过降低测量矩阵与稀疏变换矩阵Ψ之间的相关性可以提高其重构性能。两者之间相关性等价于矩阵D=ΦΨ∈Rm×n各列之间归一化互相关系数的最大值,即:

(7)
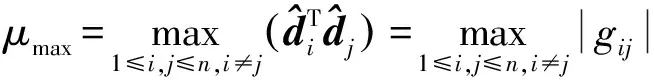
(8)
式中:gij为Gram矩阵中的元素。此时,优化目标可转化为最小化Gram矩阵的非对角元素。
文献[10]提出一种理想的状态是令μmax→0,即使Gram矩阵无限逼近同维度单位矩阵。然而,这是一种非常严格的约束条件,计算收敛速度较慢。
根据编码理论中Grassmanian框架[16]可知,测量矩阵的优化等同于一组Grassmanian框架,其目的是通过最小化最大互相关系数,使所有投影向量包含相同冗余。互相关系数存在着一个下界,即Welch界,通过使测量矩阵与稀疏变换矩阵的互相系数逼近Welch界,可使每个测量值包含等量信息,即测量值的信息熵达到最大。Welch界[17]定义为:

(9)
其中:n是稀疏变换矩阵中原子个数,m是测量数据个数。
为提高收敛速度,本文利用Welch界阈值截断Gram矩阵非对角元素,定义新的目标矩阵H:
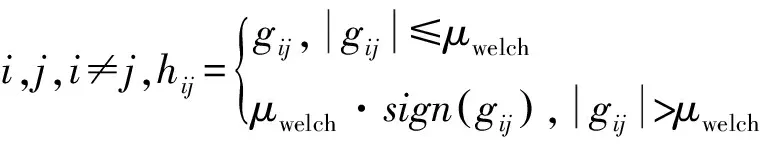
(10)
式中:hij为目标矩阵H的元素。式(10)约束了H矩阵的非对角元素,同时令H矩阵对角元素为1。
通过使Gram矩阵逼近新的目标矩阵,可建立优化目标函数为:

(11)
式(7)定义的最大相关系数μmax只能反映测量矩阵与稀疏变换矩阵的局部相关性,为更好地评价测量矩阵的整体性能,引入平均相关系数和阈值平均相关系数:
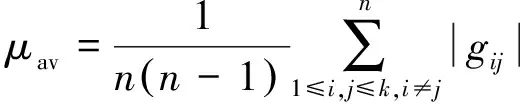
(12)
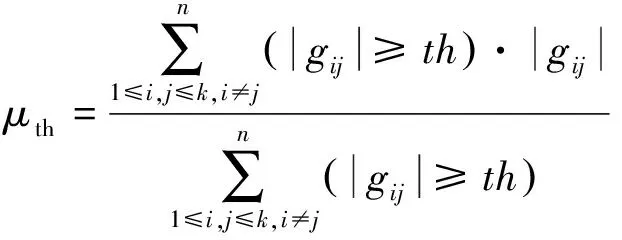
(13)
式中:本文将阈值th设置为μwelch。
3.2 粒子群优化过程
PSO算法是受鸟群捕食行为启发而发展来的一种新的群智能进化优化算法,具有收敛速度快、搜索性能好和易实现的优点[18]。不同于现有确定性迭代优化方法,PSO算法能够适应更多实际优化问题,且对优化对象没有严格的数学要求。PSO应用于块循环测量矩阵优化时,优化对象变为构造块循环矩阵的自由元向量,这在保护矩阵结构的同时能够避免基于Gram矩阵优化后逆求测量矩阵这一繁琐的计算过程。PSO算法是一种不确定性迭代求解过程,为以更大概率获得全局最优解,相应的改进型PSO算法被相继提出来。本文选用自适应权重PSO算法[19]去优化块循环测量矩阵,具体优化过程:
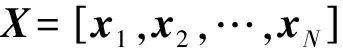
Step 2:由自由元向量构造块循环矩阵,输入稀疏变换矩阵,并计算Gram矩阵;
Step 3:构造目标矩阵H,并根据目标函数计算每个粒子的适应度J;
Step 4:比较每个粒子的适应度与其所得到的最小值,更新个体最优位置pBest和全局最优位置gBest,并计算粒子惯性权重:

Step 5:更新粒子的速度和位置
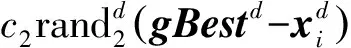
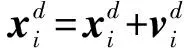
其中:rand1,2是介于(0,1)之间的随机数;c1,c2是学习因子。
4 实验结果对比与分析
为验证本文提出的基于PSO优化块循环测量矩阵在遥感压缩成像中的有效性,本节开展了相关仿真实验研究。主要包括两部分:一是对块循环测量矩阵性能优化实验;二是优化的块循环测量矩阵的重构性能对比实验。
4.1 块循环矩阵性能优化实验


图2 过完备稀疏字典
图3上图是块循环测量矩阵优化过程中目标函数值随着迭代次数的变化曲线。从图中可以看出,目标函数值在迭代过程中不断下降,经过120次迭代后函数值由最初的24收敛到18附近。图3下图(彩图见期刊电子版)是构造块循环测量矩阵的自由元向量时元素值随着迭代次数的变化情况,图中不同颜色代表不同元素。同样经过120次迭代后元素取值趋于稳定,并收敛 于[-4,4]。由此可得优化的块循环测量矩阵如图4所示。

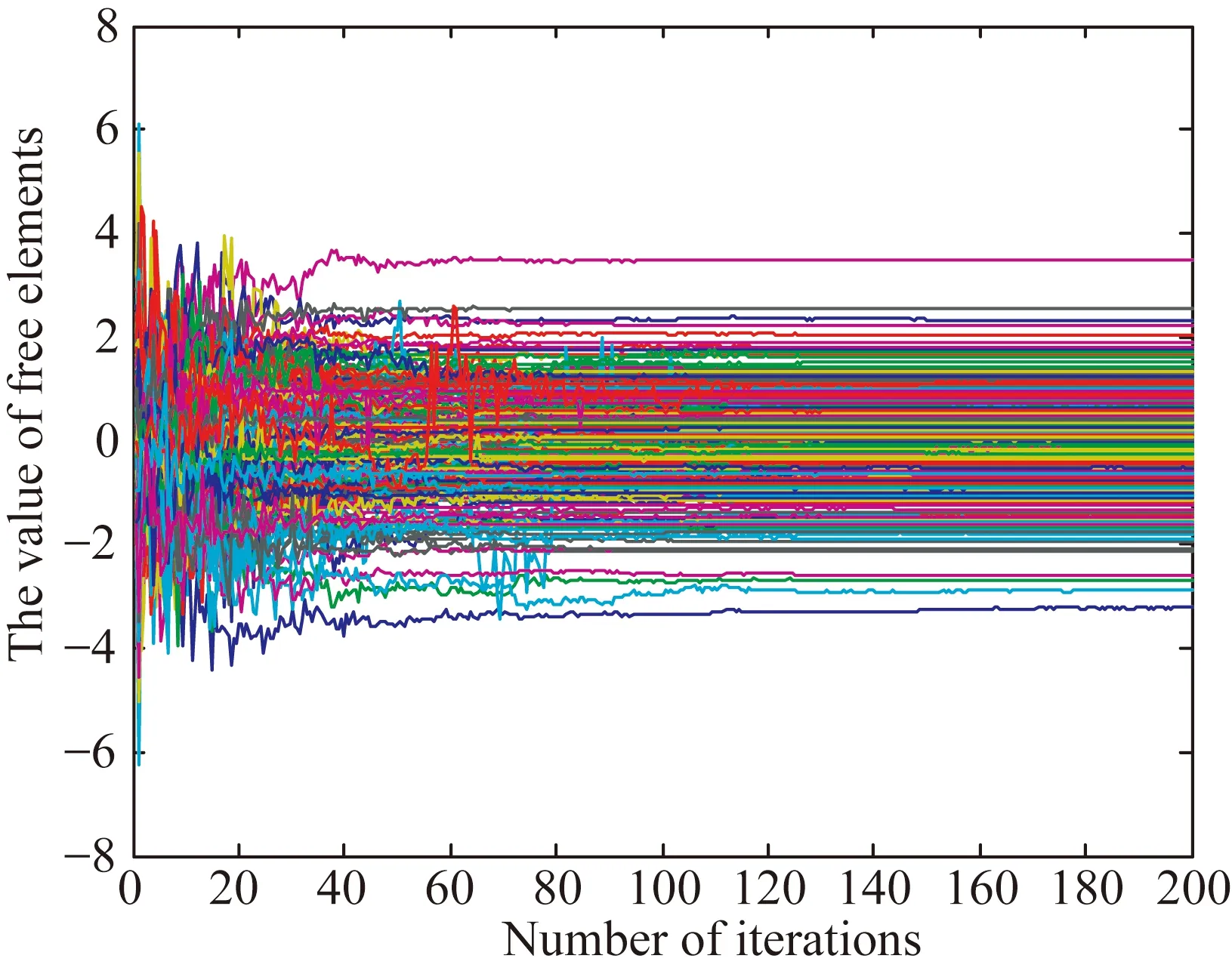
图3 目标函数值和自由元向量在迭代过程中的变化
Fig.3 Objective function and free elements change with number of iterations

图4 优化的块循环矩阵
表1给出了优化前后块循环测量矩阵相关系数的比较,以及图5的相关系数统计分布情况。从表1可以看出,优化后的块循环测量矩阵与稀疏字典之间的μmax、μav、μth值均比未优化前小。这说明优化后的块循环矩阵与稀疏字典列向量之间的相关性变小。优化后的块循环矩阵μmax值低于高斯随机矩阵,但是μth值仍大于高斯矩阵,其性能对比分析将在重构实验中作进一步讨论。
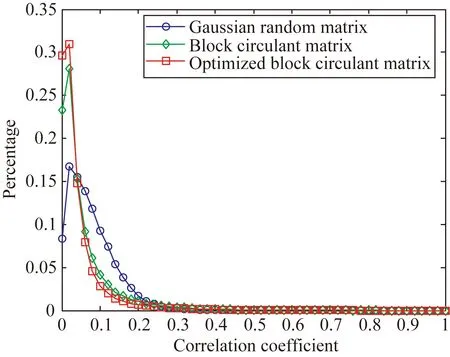
图5 测量矩阵与稀疏基相关系数统计分布
Fig.5 Statistical distribution of correlation coefficient of measurement matrix and sparse transform matrix
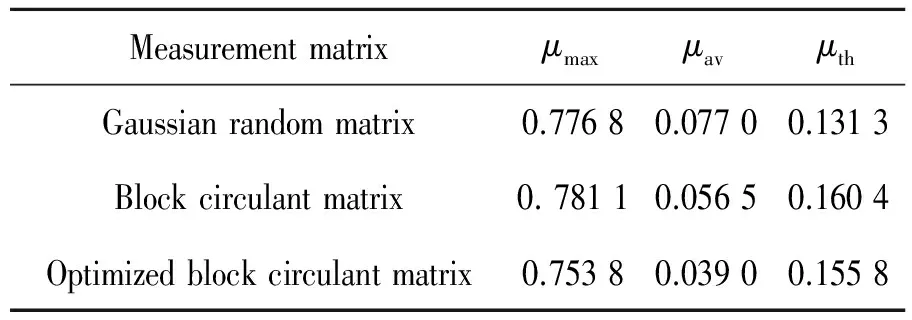
表1 测量矩阵性能对比
由图5可以看出,优化后的块循环测量矩阵与稀疏变换矩阵的相关系数统计分布的数值范围逐渐缩小,且在μwelch值附近分布更加集中。实验结果表明,本文测量矩阵优化方法能够在保持块循环矩阵结构的同时,降低其与稀疏变换矩阵的相关性,使其更加符合测量矩阵的设计要求。
4.2 优化的块循环矩阵重构性能实验
为直观地验证优化后块循环矩阵用于遥感压缩成像时的重构性能,本节开展了相关重构对比实验。实验中选取一幅512×512的遥感测试图像,如图6(a)所示。将该测试图像分成1 024 个16×16子块进行分块重构。而且通过与高斯随机测量矩阵和未优化的块循环测量矩阵的重构效果进行对比来验证其性能。稀疏变换矩阵仍采用上一节中训练得到的过完备稀疏字典,重构算法采用正交匹配追迹(Orthogonal Matching Pursuit, OMP)算法,并采用峰值信噪比(Peak Signal to Noise Ratio, PSNR)和结构相似度(Structure Similarity, SSIM)作为客观评价指标。
图6是采样率为50%的条件下,在3种不同测量矩阵得到的重构结果。其中,PSNR分别为27.234 6, 29.081 2, 29.398 5和SSIM分别为0.908 3, 0.929 1, 0.934 7。重构结果表明优化后的块循环测量矩阵的重构性能明显优于优化前;和随机高斯测量矩阵的重构结果相比,PSNR和SSIM值都比较接近,说明优化后块循环测量矩阵的重构性能接近高斯随机测量矩阵。从图中也可直观地看出在未优化的块循环测量矩阵测量下,重构图像“块效应”比较明显,且在边缘纹理区域重构效果明显差于优化后块循环测量矩阵的重构效果;优化后块循环测量矩阵的重构性能整体上接近高斯随机测量矩阵的结果。
表2是相同采样率条件下,4.1中所述遥感图像训练集中5幅具有代表性样本图像的重构结果做对比。5幅样本图像分别对应着不同特征的遥感场景,实验中统一采用图2所示的过完备稀疏字典作为变换矩阵。由对比结果同样可以看出,通过本文算法优化后的块循环测量矩阵重构性能得到了很大改善。而且第一幅和第五幅遥感图像的重构性能略高于重构性能较好的高斯随机测量矩阵。对于不同遥感图像而言,特征越复杂改善效果越明显。

(a)原始图像(a) Original image

(c)块循环矩阵(c) Block circulant matrix

(d)优化后的块循环矩阵(d) Optimized block circulant matrix
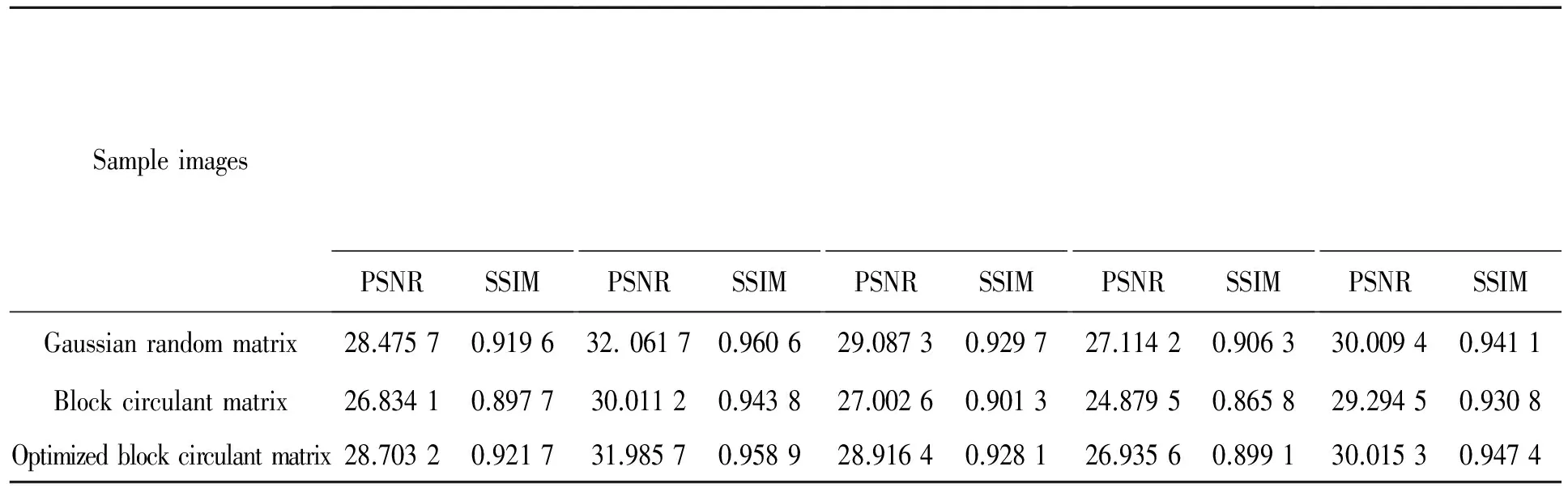
SampleimagesPSNRSSIMPSNRSSIMPSNRSSIMPSNRSSIMPSNRSSIMGaussianrandommatrix28.47570.919632.06170.960629.08730.929727.11420.906330.00940.9411Blockcirculantmatrix26.83410.897730.01120.943827.00260.901324.87950.865829.29450.9308Optimizedblockcirculantmatrix28.70320.921731.98570.958928.91640.928126.93560.899130.01530.9474
为验证优化测量矩阵对采样率的影响,比较了3种不同测量矩阵下的图像重构效果随采样率的变化情况。实验中采样率分别设置为0.20,0.25,0.30,…,0.60,每个采样率下分别进行100次实验,然后对重构图像的均方误差(Mean Square Error, MSE)取平均并求得PSNR值和每次重构图像的SSIM值的平均值,对比结果如图7所示。从图中可以看出,优化后的块循环测量矩阵的图像重构性能优于未优化的块循环测量矩阵,并接近高斯随机测量矩阵的重构性能。另外,在采样率为0.20,0.25,0.30时,优化后的块循环测量矩阵对图像的重构性能最佳,说明优化后的块循环测量矩阵能够在一定程度上降低测量数据量。
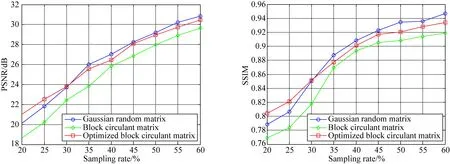
图7 重构图像效果随采样率的变化
另外,考虑到块循环矩阵子块大小与光调制器件的点扩散函数相关。表3给出了不同子块大小的块循环测量矩阵优化前后的重构结果。实验中变换矩阵仍采用图2所示的过完备稀疏字典,每种类型的块循环测量矩阵同样分别进行100次重构,并按照上述方法求其评价值。从表中可以看出,相比于未优化的块循环矩阵,优化后的不同子块大小的块循环矩阵对图像的重构性能得到了不同程度的提高。其中子块大小为16×16的块循环矩阵改善程度最佳,PSNR和SSIM分别提高了1.806 2和0.021 6,其余按优化效果由高到低依次是子块大小为64×64,32×32,8×8和128×128的块循环矩阵。同时从不同块循环矩阵的重构性能来看,子块大小为64×64块循环矩阵重构性能最佳, 而子块大小为16×16和32×32的性能也比较接近子块大小64×64的块循环矩阵。结合实验所采用的块循环矩阵规模,在实际应用中选择的子块大小相比于整个矩阵规模要适中。

表3 不同子块大小的块循环测量矩阵性能对比
5 结 论
块循环测量矩阵具有快速计算和易于实现的特点,用于遥感压缩成像具有独特优势。但考虑到它对图像重构性能仍不理想,本文从测量矩阵优化的角度出发,改善测量矩阵性能。现有测量矩阵优化方法的主要优化对象是随机测量矩阵,应用于块循环测量矩阵优化时会改变和破坏矩阵结构。本文把粒子群智能算法引入到块循环矩阵优化中,优化对象改为构造矩阵的自由元向量。同时为提高优化效率,以逼近作为目标矩阵的Welch阈值截断的Gram矩阵的方式,建立目标函数。优化实验结果表明,优化后的测量矩阵在保持块循环结构的同时,其与稀疏变换矩阵的最大相关系数、平均相关系数和阈值平均相关系数分别降低了0.027 3、0.017 5和0.004 6。重构实验表明,优化的块循环矩阵能够在一定程度上提高图像重构性能。
[1] 严奉霞,朱炬波,刘吉英,等. 光学遥感压缩成像技术[J].航天返回与遥感, 2014, 35(1): 54-62,96. YAN F X, ZHU J B, LIU J Y,etal.. Compressive imaging techniques in optical remote sensing [J].SpacecraftRecovery&RemoteSensing, 2014, 35(1): 54-62,96.(in Chinese)
[2] 范晋祥,岳艳军. 军用红外成像系统新概念新体制的发展[J]. 红外与激光工程,2011, 40(1): 1-6. FAN J X, YUE Y J. Development in new concepts and new schemes for military infrared imaging systems [J].InfraredandLaserEngineering, 2011, 40(1): 1-6.(in Chinese)
[3] DONOHO D L. Compressed sensing [J].IEEETransactionsonInformationTheory, 2006, 52(4): 1289-1306.
[4] 陈涛,李正炜,王建立,等. 应用压缩传感理论的单像素相机成像系统[J]. 光学 精密工程, 2012, 20(11): 2523-2530. CHEN T, LI ZH W, WANG J L,etal.. Imaging system of single pixel camera based on compressed sensing [J].Opt.PrecisionEng., 2012, 20(11): 2523-2530.(in Chinese)
[5] 王朋,荣志斌,何俊华,等. 基于压缩感知的偏振光成像技术研究[J]. 红外与激光工程,2016, 45(2): 0228005. WANG P, RONG ZH B, HE J H,etal.. Polarization imaging based on compressed sensing theory [J].InfraredandLaserEngineering, 2016, 45(2): 0228005.(in Chinese)
[6] MARCIA R F, HARMANY Z T, WILLETT R M. Compressive coded aperture imaging [C].ProceedingofSPIE, 2009, 72460G.
[7] 王忠良,冯燕,肖华,等. 高光谱图像的分布式压缩感知成像与重构[J]. 光学 精密工程, 2015, 23(4): 1131-1137. WANG ZH L, FENG Y, XIAO H,etal.. Distributed compressive sensing imaging and reconstruction of hyperspectral imagery [J].Opt.PrecisionEng., 2015, 23(4): 1131-1137.(in Chinese)
[8] CANDES E. The restricted isometry property and its implications for compressed sensing [J].ComptesRendusMathematique, 2008, 346(9): 589-592.
[9] ELAD M. Optimized projections for compressed sensing [J].IEEETransactionsonSignalProcessing, 2007, 55(12): 5695-5703.
[10] ABOLGHASEMI V, FERDOWSI S, SANEI S. A gradient-based alternating minimization approach for optimization of the measurement matrix in compressive sensing [J].SignalProcessing, 2012, 92(3): 999-1009.
[11] 郑红,李振,黄盈. 一种基于拟牛顿法的CS投影矩阵优化算法[J]. 电子学报,2014, 42(10): 1977-1982. ZHENG H, LI ZH, HUANG Y. An optimization method for CS projection matrix based on quasi-Newton method [J].ActaElectronicaSinica, 2014, 42(10): 1977-1982.(in Chinese)
[12] RAMIREZ A, ARGUELLO H, ARCE G R,etal.. Spectral image classification from optimal coded-aperture compressive measurements [J].IEEETransactionsonGeoscienceandRemoteSensing, 2014, 52(6):3299-3309.
[13] RAMIREZ A, ARCE G R, SADLER B M. Spectral image unmixing from optimal coded-aperture compressive measurements[J].IEEETransactionsonGeoscienceandRemoteSensing, 2015, 53(1): 405-415.
[14] 郭静波,汪韧. 交替寻优生成元素幅值结合混沌随机相位构造循环测量矩阵[J]. 物理学报,2015, 64(13): 1-12. GUO J B, WANG R. Constructing circulant measurement matrix through alternating optimizing amplitudes together with chaotic stochastic phases of the matrix generating elements [J].ActaPhysicaSinica, 2015, 64(13): 1-12.(in Chinese)
[15] KITTLE D, CHOI K, WAGADARIKAR A,etal.. Multiframe image estimation for coded aperture snapshot spectral imagers [J].Appl.Opt., 2010, 49(36): 6824-6833.
[16] STROHMER T, HEATH R W. Grassmannian frames with applications to coding and communication [J].AppliedandComputationalHarmonicAnalysis, 2003, 14(3):257-275.
[17] WELCH L. Lower bounds on the maximum cross correlation of signals [J].IEEETransactionsonInformationTheory, 1974, 20(3): 397-399.
[18] KENNEDY J, EBERIIART R C. Particle swarm optimization[C].IEEEInternationalConferenceonNeuralNetworks, 1995, 4: 1942-1948.
[19] ZHENG Q, FAN Y. Adaptive inertia weight particle swarm optimization[C].ICAISC, 2006, 4029: 450-459.

陶会锋(1988-),男,河北邯郸人,博士研究生, 2011年、2014年于电子工程学院分别获得学士、硕士学位,主要从事光学信号获取与处理方面的研究。E-mail: taohfeei@163.com

杨 星(1983-),男,四川都江堰人,助理研究员, 2006年、2012年于电子工程学院分别获得学士、博士学位,主要从事模式识别和人工智能方面的研究。E-mail: yangxing1983@163.com
导师简介:

凌永顺(1937-),男,安徽定远人,研究员,院士, 1960年于北京师范大学获得学士学位,主要从事光学工程方面的研究。E-mail: Lyseei@163.com
(版权所有 未经许可 不得转载)
Structured measurement matrix by particle swarm optimization for remote sensing compressive imaging
TAO Hui-feng1,2*, YANG Xing1,2, CHEN Jie3, LING Yong-shun1,2, YIN Song-feng1,2
(1.State Key Laboratory of Pulsed Power Laser Technology,ElectronicEngineeringInstitute,Hefei230037,China;2.KeyLaboratoryofInfraredandLowTemperaturePlasmaofAnhuiProvince,ElectronicEngineeringInstitute,Hefei230037,China;3.DepartmentofElectronicsandInformationEngineering,AnhuiJianzhuUniversity,Hefei230601,China)
For non-ideal image construction performance of a block circulant matrix in remote sensing compressive imaging, this paper introduces the particle swarm optimization intelligent algorithm into optimizing the block circulant matrix, meanwhile maintaining the matrix structure. Firstly, the Welch bound of a correlation coefficient is taken as a threshold value to restrain the off-diagonal entries of the Gram matrix and to build a target matrix. Then, the objective function is established by making the Gram matrix approach the target matrix, and the optimized variable is replaced as the free entries to compose the block circulant matrix. To improve the optimized efficiency, the weight adaptive update is used to improve the partical search capacity. A construction comparison experiment is carried out, the results show that the correlation properties of the block circulant matrix with the sparse transform matrix has been reduced while maintaining the matrix structure, and the coefficients for maximum correlation, average correction and threshold average correction have been reduced by 0.027 3, 0.017 5 and 0.004 6, respectively. These results show the image construction performance is improved by optimized block circulant matrix.
remote sensing image; compressive imaging; image reconstruction; block circulant matrix; particle swarm optimization
2016-07-14;
2016-09-09.
国家自然科学基金资助项目(No.61503394);安徽省自然科学基金资助项目(No.1408085QF131,No.1508085QF121);安徽高等学校自然科学研究项目(No.KJ2015ZD14,No.KJ2016A149)
1004-924X(2016)11-2821-09
TP751
A
10.3788/OPE.20162411.2821
*Correspondingauthor,E-mail:taohfeei@163.com
