飞秒激光跟踪仪光轴与竖轴同轴度的标定

2016-12-19崔成君劳达宝高书苑郝春艳周维虎

光学精密工程 2016年11期

崔成君，劳达宝，高书苑，郝春艳，周维虎，，4*

(1.长春理工大学光电工程学院，吉林长春 130009；2.中国科学院光电研究院，北京 100094；3.合肥工业大学仪器科学和光电工程学院，安徽合肥 230009；4.中国科学院大学，北京 100049)

飞秒激光跟踪仪光轴与竖轴同轴度的标定

崔成君1，劳达宝2，高书苑3，郝春艳1，周维虎1，2，4*

考虑飞秒激光跟踪仪仪器轴系的几何误差会影响仪器的指向精度并最终影响坐标测量精度，本文研究了激光光轴与竖轴的几何误差对仪器测量精度的影响。提出了激光光轴与竖轴的同轴度标定方法，以降低其不重合带来的跟踪测量误差。首先，基于几何光学原理建立了光轴与竖轴的几何误差模型，分别分析了光轴与竖轴的倾斜与平移误差对仪器测角精度的影响。然后，针对设计的仪器提出了基于旋转成像原理的光轴与竖轴同轴度的检测方法，并设计了一套同轴度检测装置。最后，基于该检测装置，通过调节两组双光楔完成了激光光轴与竖轴的倾斜与平移误差的标定。结果显示，经标定校准后激光光轴与竖轴的角度误差为3.4″；平移误差为26.1 μm，得到的结果为仪器后续建立误差补偿模型奠定了基础。

飞秒激光跟踪仪；同轴度；旋转成像；双光楔；标定

1 引言

飞秒激光跟踪仪是在传统激光跟踪仪的基础上，通过采用最先进的飞秒激光测距原理来增大测量范围并提高精度和测量速度。它突破了传统测距在测程、精度和测量速度方面难以协调的瓶颈，从根本上解决了长期困扰测距技术的问题，是对传统测距技术的一次革命，也是大型科学工程和大型高端装备制造中急需的测量装备[1-4]。

飞秒激光跟踪仪通过测量仪器到目标反射靶球的距离和角度来确定目标的空间位置。仪器的轴系结构包括横轴、竖轴及激光光轴3个部分，理想情况下这3个轴的几何关系为横轴与竖轴正交，光轴与竖轴重合[5-6]。但实际中由于受到机械加工等条件的限制，轴系之间存在误差，从而直接影响仪器的指向精度和跟踪性能[7-9]。由于仪器的激光光束中心线难以实现直接测量，仪器的激光光轴与竖轴的偏移量也较难直接精确测量，从而无法实现精确的调节。2003年，李杏华等研究了基于多边法的激光跟踪干涉测量系统，分析了影响系统测量精度的单个激光跟踪头的误差源，基于四象限光电池来调节光束入射点与旋转中心点的重合度，将偏差控制在0.5 mm以内[10]。2012年，张亚娟针对单站式激光跟踪坐标测量系统，提出了通过判断反射光在接收屏上的轨迹形状来调整跟踪转镜的安装偏差和激光光束与机械竖轴的对准误差的方法，不过此方法测量误差较大，而且在标定过程中还可能存在激光光束假对准现象[11]。上述方法并不适用于飞秒激光跟踪仪竖轴与激光光轴的同轴度调节。鉴于此，本文针对飞秒激光跟踪仪提出了一种基于旋转成像原理的激光光轴与竖轴同轴度检测方法，对仪器进行精确装调，以降低激光光轴与竖轴的不重合而带来的跟踪测量误差。

2 工作原理

飞秒激光跟踪仪的工作原理如图1所示。首先在被测目标点上安置一个反射靶球，然后将仪器发出的激光瞄准目标靶球，当目标带着靶球一起移动时，仪器发出的激光光束始终对准靶球中心，保持实时跟踪。此时，通过测量仪器到靶球的距离和角度来确定目标的空间位置。

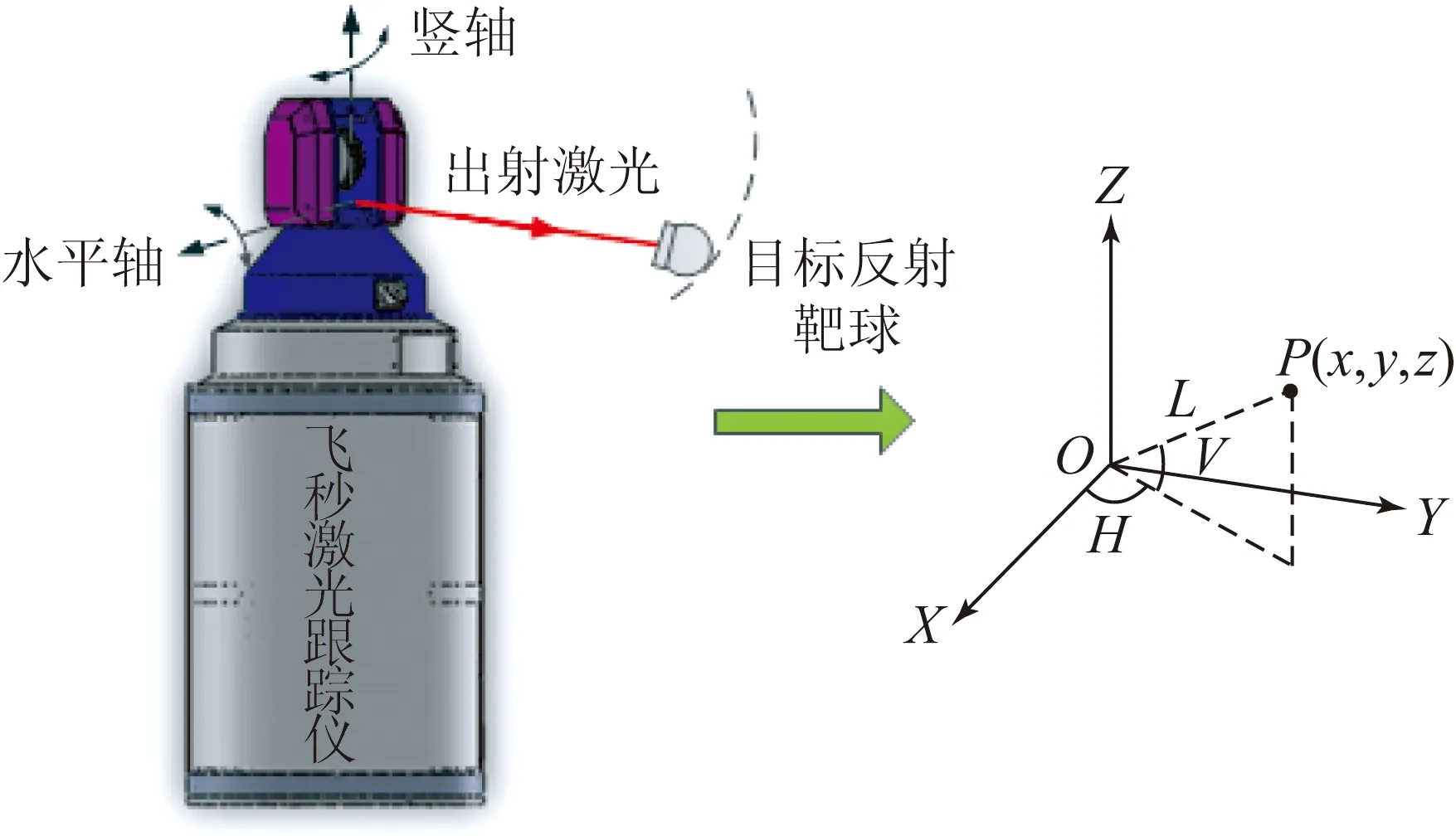
图1 飞秒激光跟踪仪的目标空间坐标测量原理

Fig.1 Principle of object spatial location measurement using femtosecond laser tracker

如图1所示，O-XYZ是以飞秒激光跟踪仪为基准建立的测量坐标系，X轴表示仪器的水平轴方向，Z轴表示仪器的竖轴方向，O为仪器水平轴与竖轴的交点。当已知被测目标P与仪器的距离L、水平角H和垂直角V时，根据式(1)～式(3)即可计算P点的空间坐标：

x=L·cosV·cosH，

(1)

y=L·cosV·sinH，

(2)

z=L·sinV，

(3)

其中：(x，y，z)为被测目标在测量坐标系下的坐标。由上述公式可知，目标的测量精度主要与测距精度和测角精度有关。

3 几何误差分析

飞秒激光跟踪仪轴系的几何误差包括水平轴和竖轴的不垂直误差和不相交误差、跟踪反射镜与水平轴的偏角误差和平移误差以及光轴与竖轴的夹角误差和平移误差等。激光光轴与竖轴的几何误差主要包括平移误差和倾斜误差，本文通过几何光学原理建立其误差模型，分析了误差对仪器测角精度的影响。

3.1 光轴平移误差

激光光轴与竖轴的平移误差模型如图2所示，其中X轴表示仪器的水平轴方向，仪器的竖轴方向为垂直纸面。

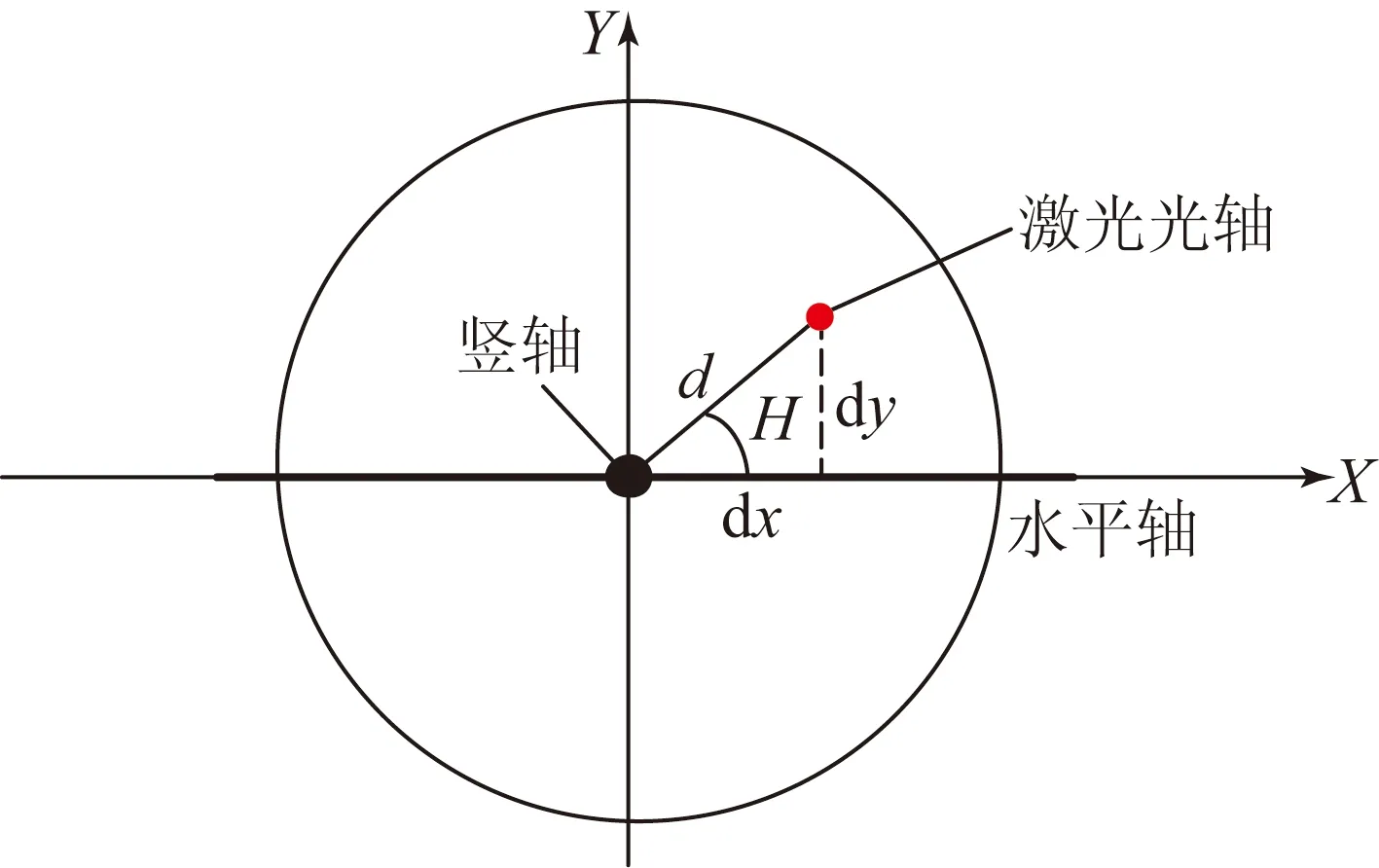
图2 光轴平移误差模型

当仪器的出射激光光轴位于(H，V)方位时，如图2所示，光轴的平移误差可分解为：

dx=d·cosH，

(4)

dy=d·sinH，

(5)

其中：d为光轴与竖轴的距离；dx为光轴平移误差在水平轴方向上的分量；dy为光轴平移误差在垂直于水平轴方向上的分量。

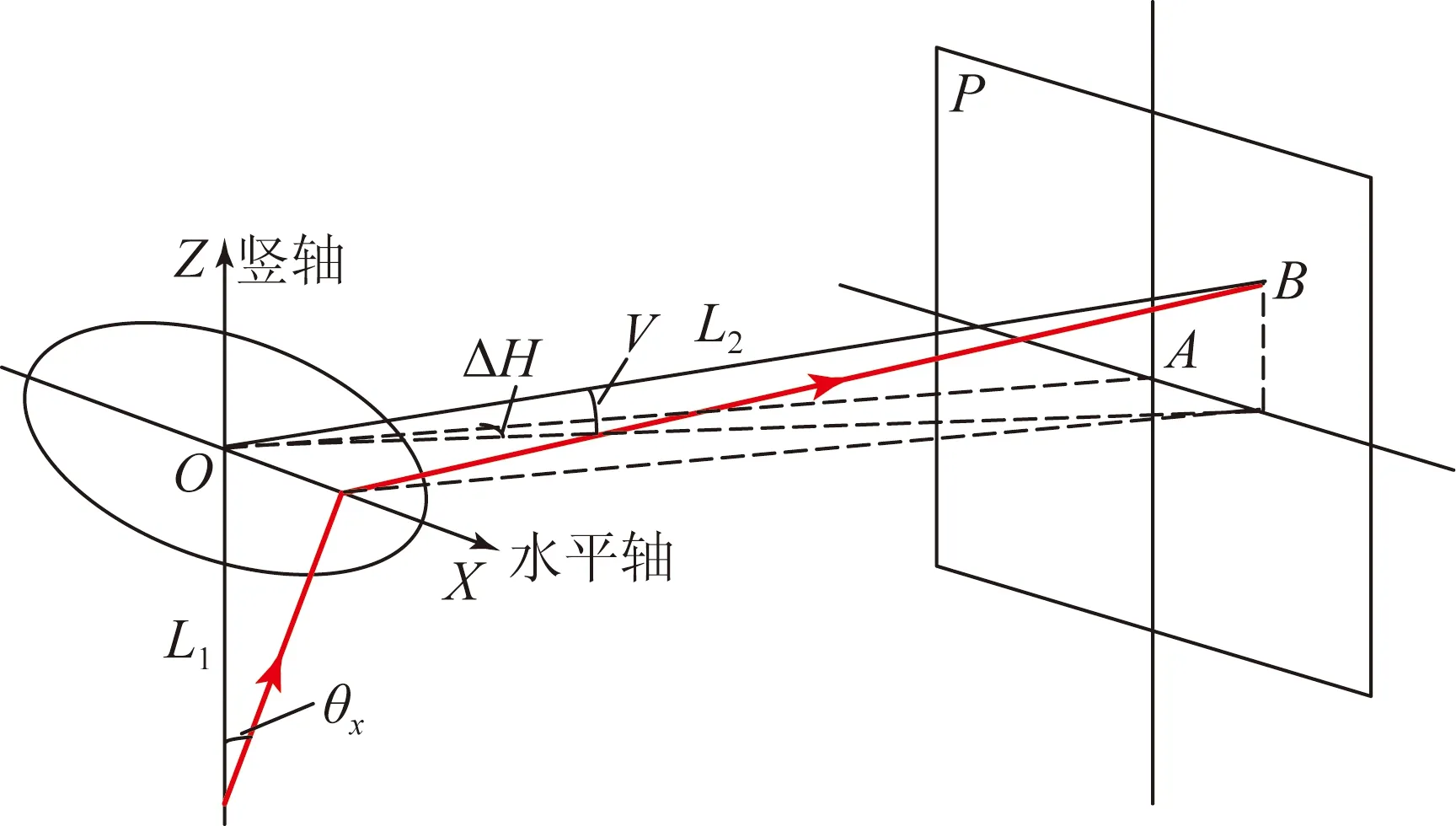
由空间几何关系可知，光轴平移误差的dx分量只对水平角测量产生影响，而dy分量则只对俯仰角测量产生影响，因此它们对仪器测角精度的影响分别如图3(a)和3(b)所示。图中P平面平行于XOZ平面，在理想情况下，仪器的出射激光光束在P平面上的投影点为A，但由于存在光轴平移误差，实际交点变为B。

(a)水平误差

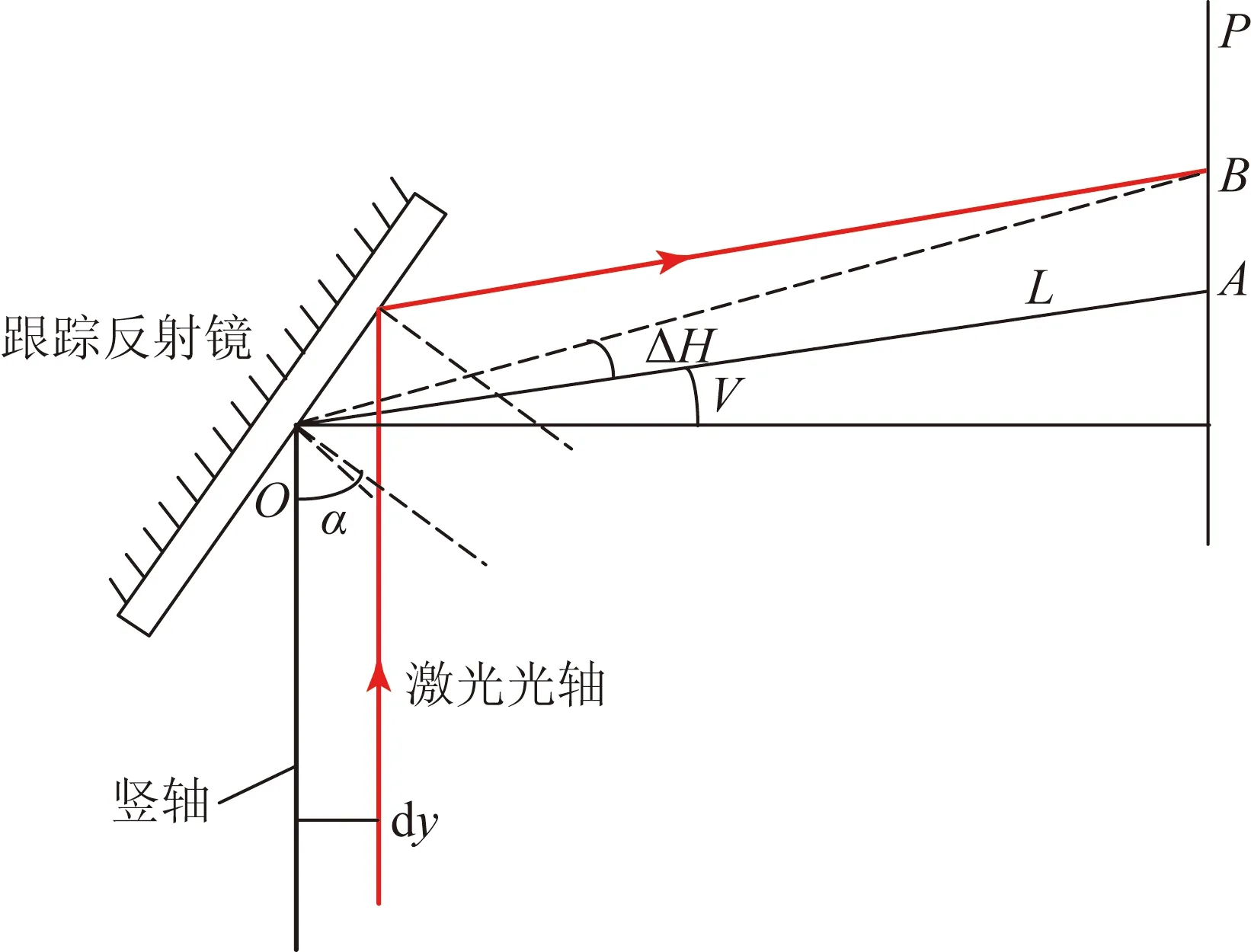
(b)俯仰角误差

Fig.3 Model of angle measurement error caused by translation of optical axis

由图3中的几何关系可知，光轴平移误差dx和dy引起的水平角、俯仰角测量误差ΔHt和ΔVt分别为：

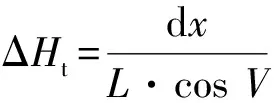
(6)

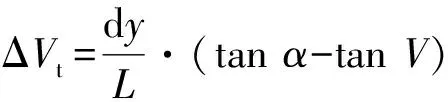
(7)

其中：L为仪器到目标的距离；α为跟踪反射镜法线与竖轴间的夹角。

3.2 光轴倾斜误差

激光光轴与竖轴的倾斜误差模型如图4所示，其中X轴表示仪器的水平轴方向，Z轴表示仪器的竖轴方向，O为坐标原点。

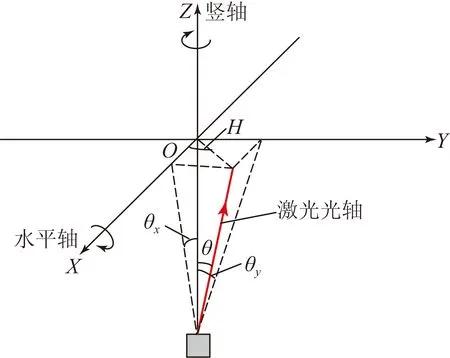
图4 光轴倾斜误差模型

当仪器的出射激光光轴位于(H，V)方位时，光轴与竖轴的倾斜误差θ可用XOZ平面上的分量θx和YOZ平面上的分量θy来表示，则有：

θx=tanθ·cosH，

(8)

θy=tanθ·sinH.

(9)

光轴倾斜误差分量θx和θy对仪器测角精度的影响分别如图5(a)和5(b)所示。图中P平面与XOZ平面平行，在理想情况下，仪器的出射激光光束在P平面上的投影点为A，但由于存在光轴倾斜误差，实际交点变为B。

(a)激光倾斜误差θx

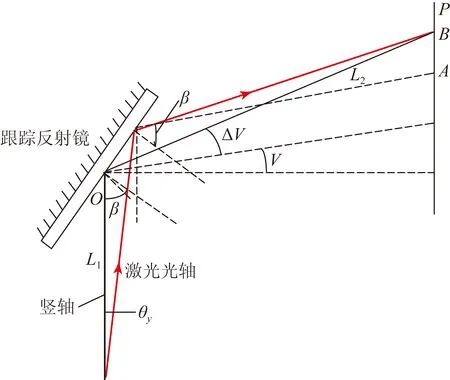
(b)激光倾斜误差θy

由图5中的几何关系可知，光轴倾斜误差θx和θy引起的水平角、俯仰角测量误差ΔHT和ΔVT分别为：

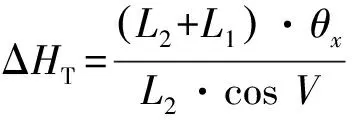
(10)

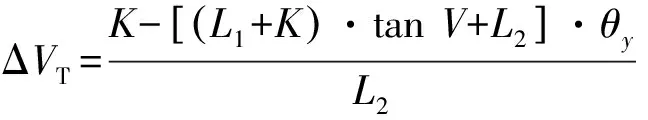
(11)

4 标定原理

本文基于上述误差模型提出了一种基于旋转成像原理的同轴度检测方法，通过该方法对仪器的光轴与竖轴的偏移量(包括平移和倾斜)进行检测，并基于该检测原理通过调节两组双光楔来进行光轴与竖轴的同轴度标定[12]，标定原理如图6所示。

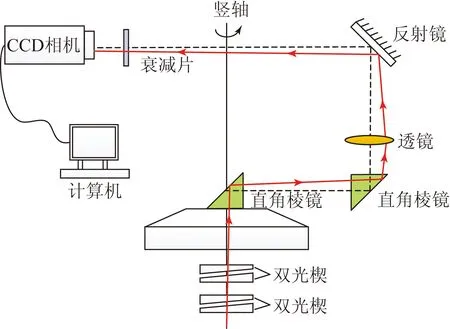
图6 光轴与竖轴的同轴度标定原理

Fig.6 Principle for coaxiality calibration of optical axis and vertical shaft

同轴度检测系统由直角棱镜、透镜、反射镜、衰减片和CCD相机组成，其中CCD相机位于透镜的焦平面处。直角棱镜与反射镜用于折转光路，以减小系统的结构体积；透镜用于成像，将激光光束聚焦到CCD相机上，以便进行探测；衰减片用于遮挡环境光，以提高激光光斑的探测精度；计算机用于处理测量数据。激光跟踪仪发出的激光光束经两个直角棱镜反射后入射到透镜上，经透镜聚焦并由反射镜反射后最终由CCD相机接收。水平旋转竖轴，观察CCD上会聚光斑的移动轨迹，当激光光轴与竖轴存在夹角时光斑轨迹为圆形，此时通过调节激光光轴的方位使CCD上的光斑轨迹保持不变，则激光光轴与竖轴平行。然后将CCD相机离焦，水平旋转竖轴，当CCD相机在透镜焦平面和离焦后的两个位置上时光斑移动轨迹始终不变，此时仪器的竖轴与激光光轴重合。

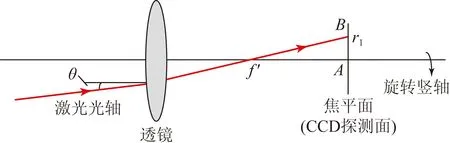
激光光轴与竖轴的夹角检测原理如图7(a)所示，此时CCD探测面与透镜焦平面重合。当光轴与竖轴重合或平行时，根据几何成像原理可知，光线经透镜聚焦后在CCD探测面上的聚焦点为A，而该点的位置不随竖轴的旋转而发生改变。如果光轴与竖轴间存在微小夹角θ时，则激光光束经透镜聚焦后在CCD探测面上的交点为B，且该点的位置随竖轴的旋转形成圆形轨迹，其轨迹半径r1可表示为：

r1=f′·tanθ，

(12)

其中：f′为透镜的焦距，则通过测量光斑轨迹的半径r1即可计算出光轴与竖轴的倾斜误差。由式(12)可知，夹角θ与光斑轨迹的半径成正比，与透镜的焦距成反比。

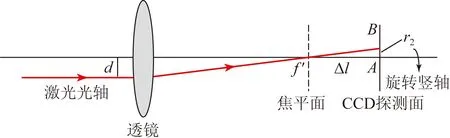
激光光轴与竖轴的平移测量原理如图7(b)所示。在校准好倾斜误差的情况下，向后平移CCD相机，使CCD探测面与透镜焦平面偏离Δl。此时只有激光光轴与竖轴重合，CCD探测面上的光斑位置才不随竖轴的旋转而发生改变。如果光轴与竖轴存在微小的平移量d，则经透镜聚焦后在CCD探测面会聚光斑会随竖轴的旋转形成圆形轨迹，其轨迹半径为：

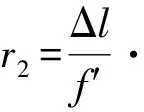
(13)

则通过测量激光光斑的轨迹半径r2即可计算出光轴与竖轴的平移误差。由式(13)可知，光轴与竖轴的平移误差与光斑轨迹半径r2和透镜的焦距成正比，与离焦量Δl成反比。

(a)光轴与竖轴夹角测量

(b)光轴与竖轴平移测量

5 同轴度校准

由上述分析可知，激光光轴与竖轴的倾斜与平移量的检测精度对透镜焦距的要求刚好相反。对于角度测量，透镜的焦距越大，调节精度越高；而对于平移误差，透镜的焦距越小，调节误差越小。由于透镜的焦距还影响检测系统的体积，所以本文选用的透镜口径为25.4 mm，焦距为250 mm；CCD相机靶面尺寸为12 mm×12 mm，像元尺寸为4 μm。由于仪器的通光孔较小，所以直角棱镜采用胶黏的方式固定；同时为了减小检测装置的质量，反射镜的底座及CCD相机的底座采用四根圆柱进行支撑，本文所设计的激光光轴与竖轴同轴度检测装置如图8所示。

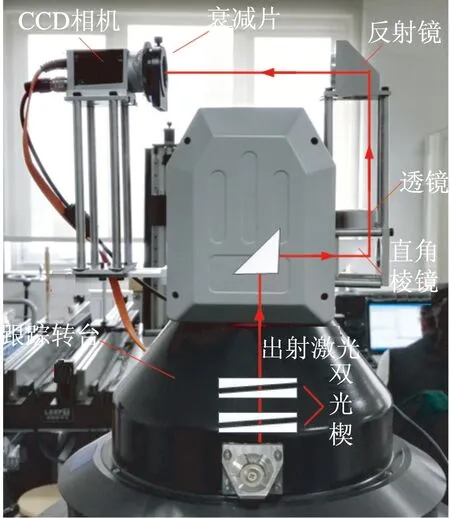
图8 激光光轴与竖轴同轴度标定装置

由于本文提出的光轴与竖轴同轴度标定方法属于相对测量法，只需计算光斑间的相对位置，不需要保证激光光束与CCD探测面的几何中心保持严格重合，所以对各个元器件的安装精度要求并不高，通过机械公差保证即可满足要求。

首先将光学元件安装到各自相应的支座上，并将装好的支座和CCD相机安装到跟踪转台上，调节CCD相机的位置使其刚好位于透镜的像方焦平面处。其次水平旋转一周竖轴，取均匀分布的8个位置，在CCD上分别记录8个位置处的激光会聚光斑图像，如图9(a)所示。最后，通过对记录光斑图像分别进行光斑中心位置提取。由于激光会聚光斑图像近似圆形，所以本文采用质心法来提取光斑的中心位置。通过反复调节图8中的两组双光楔，使激光会聚光斑的移动轨迹最小化，并提取激光光斑的质心位置。为了减小人为操作误差，本文共进行了3组测量，重复性良好，其测量结果如表1所示。

(a)焦平面光斑

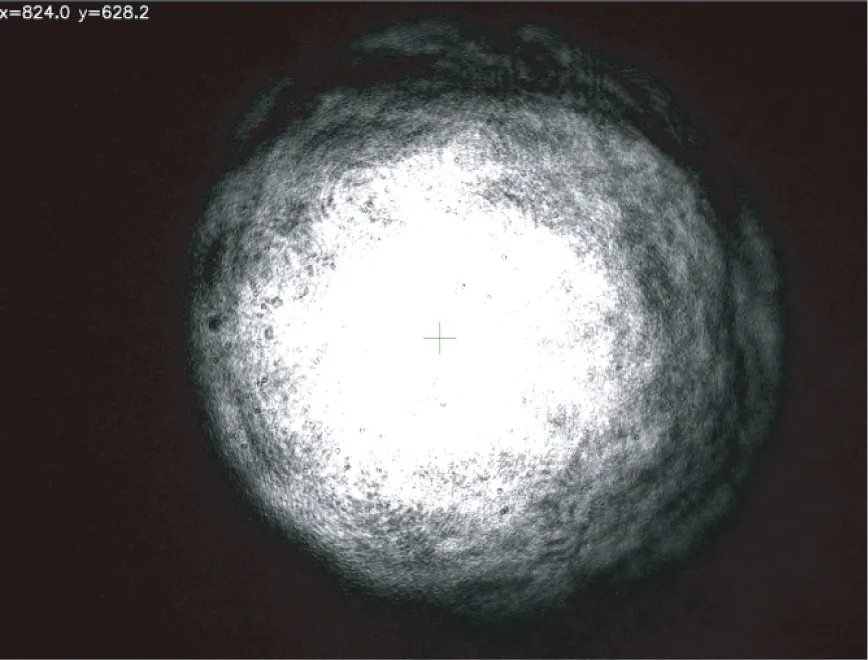
(b)离焦后光斑

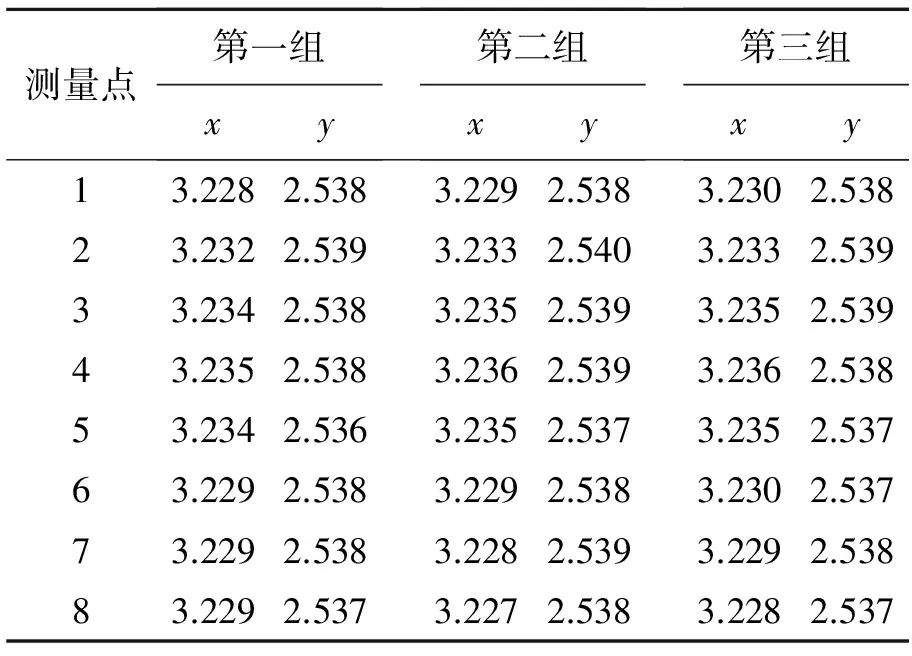
Tab.1 Centroid positions of laser facula in tilt error measurement (mm)

将表1中的3组测量数据进行曲线拟合，求得最大光斑轨迹的半径分别为4，4.5，3.9 μm。将测量结果取平均后带入式(12)即可算出光轴与竖轴的倾斜误差为3.4″。

在标定好光轴与竖轴间的倾斜误差后，使CCD探测面向后离焦60 mm。与倾斜误差测量步骤相同，将竖轴水平旋转一周，取均匀分布的8个位置，并在CCD上分别记录8个位置处的激光会聚光斑图像，如图9(b)所示。由于CCD探测面进行了离焦，所以激光光斑也按相应的比例变大。同样通过反复调节两组双光楔，使会聚激光光斑的移动轨迹最小化，并提取激光光斑的质心位置。3次测量的结果如表2所示。

表2 平移误差测量时激光光斑的质心位置

Tab.2 Centroid position of laser facula in translation error measurement (mm)

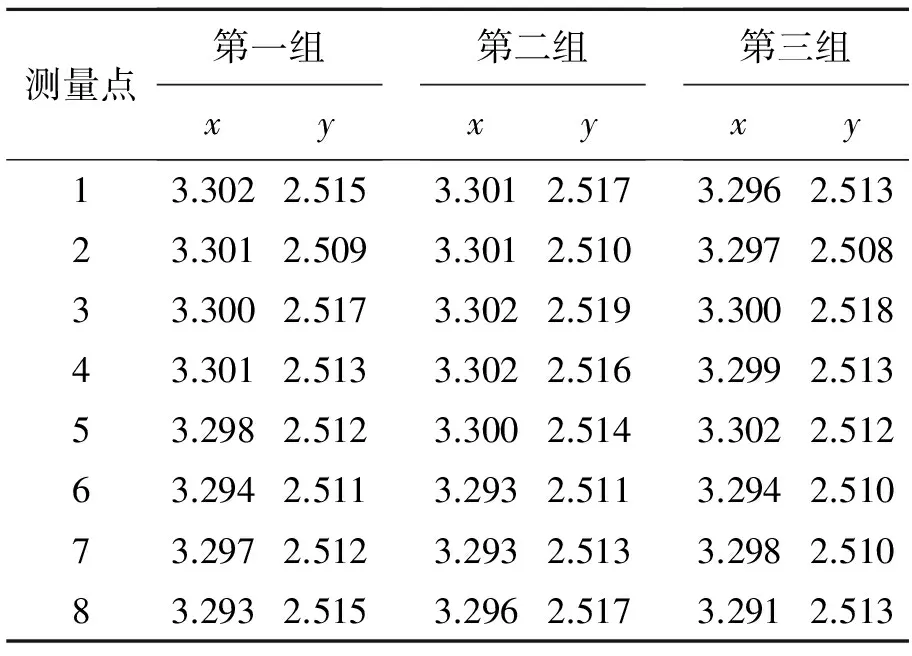
同理，将表2中的3组测量数据进行曲线拟合，求得最大光斑轨迹的半径分别为6.1，6.2，6.5 μm。将测量结果取平均带入式(13)即可算出光轴与竖轴的平移误差为26.1 μm。

6 结论

本文主要研究了飞秒激光跟踪仪的光轴与竖轴的同轴度标定方法。基于几何光学原理建立了光轴与竖轴的几何误差模型，并分析了误差对仪器测角精度的影响；设计了一套基于旋转成像原理的同轴度检测系统，可同时实现角度和平移的检测，并基于该检测系统完成了光轴与竖轴同轴度的标定。结果显示，激光光轴与竖轴的倾斜误差为3.4″，平移误差为26.1 μm。目前，受限于光学系统的分辨率，只通过机械公差及调节精度很难保证仪器的设计指标要求。为了提高仪器的测量精度，还需通过误差补偿来修正仪器轴系的几何误差。本文的测量结果为后续误差补偿模型的建立奠定了基础。

[1] 李锐钢.基于激光跟踪仪标定五轴数控加工中心主轴[J]. 光学精密工程，2012，20(3)：477-482. LI R G.Calibration of tool spindle for 5-axis CNC machine using laser tracker [J].Opt.PrecisionEng.，2012，20(3)：477-482.(in Chinese)

[2] KLAUS W， MATTHIAS F， FRANK H. Measuring large 3D structures using four portable tracking laser interferometers [J].Measurement， 2012， 45：2339-2345.

[3] 李迎伟，李明，张靓，等. 激光跟踪测量技术在地铁检测中的应用[J].机械设计与制造，2007(7)：98-100. LI Y W， LI M， ZHANG L，etal.. Technology of laser tracker and its application in subway train’s testing [J].MachineryDesignandManufacture，2007(7)：98-100.(in Chinese)

[4] 马强，闫勇刚，刘万里，等. 激光跟踪测量系统校验及在三维测量中的应用[J]. 中国测试技术，2006，32(2)：27-29. MA Q， YAN Y G， LIU W L，etal.. Inspection of laser tracking system and its application in three-dimensional measurement [J].ChinaMeasurementTechnology，2006，32(2)：27-29.(in Chinese)

[5] 周维虎，费业泰，李百源，等.激光跟踪仪几何误差修正[J].仪器仪表学报，2002，23(1)：56-60. ZHOU W H， FEI Y T， LI B Y，etal.. The correction of geometric error for laser tracker [J].ChineseJournalofScientificInstrument，2002，23(1)：56-60.(in Chinese)

[6] 张滋黎，朱涵，周维虎. 激光跟踪仪转镜倾斜误差的标定及修正[J]. 光学精密工程，2015，23(5)：1205-1212. ZHANG Z L， ZHU H， ZHOU W H. Error calibration and correction of mirror tilt in laser trackers [J].Opt.PrecisionEng.，2015.23(5)：1205-1212.(in Chinese)

[7] 张智永，周晓尧，范大鹏. 光电探测系统指向误差分析建模与修正[J]. 航空学报， 2011，32(11)：2042-2054. ZHANG ZH Y， ZHOU X Y， FAN D P. Analysis， modeling and correction of pointing errors for electro-optical detection systems [J].ActaAeronauticaetAstronauticaSinica， 2011，32(11)：2042-2054. (in Chinese)

[8] 刘娇月，杨聚庆，董登峰，等. 激光跟踪仪的光电瞄准与定位系统[J]. 光学精密工程，2015，23(6)：1558-1564. LIU J Y， YANG J Q， DONG D F，etal.. Optoelectronic aiming and orientation system of laser tracker [J].Opt.PrecisionEng.，2015，23(6)：1558-1564. (in Chinese)

[9] 董登峰，周维虎，纪荣祎，等. 激光跟踪仪精密跟踪系统研究与设计[J]. 光学精密工程，2016，24(2)：309-318. DONG D F， ZHOU W H， JI R Y，etal.. Design of precise tracking system of laser tracker [J].Opt.PrecisionEng.，2016，24(2)：309-318.(in Chinese)

[10] 李杏华.激光跟踪系统的设计[D]. 天津：天津大学，2003. LI X H.DesignofaLaserTrackingSystem[D]. Tianjin：Tianjin University， 2003. (in Chinese)

[11] 张亚娟. 单站式激光跟踪坐标测量系统研究[D]. 天津：天津大学，2012. ZHANG Y J.StandAloneLaserTrackingSystem[D]. Tianjin：Tianjin University， 2012. (in Chinese)

[12] CUI C J， ZHOU W H， LAO D B，etal.. Method of light path alignment for femtosecond laser tracker based on double optical wedge [J].SPIE， 2015，9623：96230E.

崔成君(1988-)，男，吉林人，博士研究生，2010年、2013于长春理工大学分别获得学士、硕士学位，主要研究方向为光电精密测量技术、光电系统总体设计与集成测试技术。E-mail：ccj408@126.com

导师简介：

周维虎(1962-)，男，安徽合肥人，研究员， 2000年于合肥工业大学获得博士学位，主要研究方向为光电系统总体设计与集成测试、飞秒激光测量技术、光电精密测量技术以及大尺寸几何量计量测试技术。E-mail：zhouweihu@aoe.ac.cn

Calibration for coaxiality of optical axis and vertical rotary shaftin femtosecond laser tracker

CUI Cheng-jun1， LAO Da-bao2， GAO Shu-yuan3， HAO Chun-yan1， ZHOU Wei-hu1，2，4*

(1. College of Photoelectrical Engineering，ChangchunUniversityofTechnology，Changchun130009，China；2.AcademyofOpto-electronics，ChineseAcademyofSciences，Beijing100094，China；3.SchoolofInstrumentScienceandOpto-electronicEngineering，HefeiUniversityofTechnology，Hefei230009，China；4.UniversityofChineseAcademyofSciences，Beijing100049，China)

As the geometric errors of shafts in a femtosecond laser tracker directly lead to pointing error and limits the coordinate measuring accuracy of the instrument， this paper researches the effects of geometric errors between optical axis and vertical rotary shaft in the laser tracker on measuring accuracy of the instrument. It proposes a calibration method for the coaxiality of optical axis and vertical rotary shaft to reduce the tracking measuring errors from the misalignment between optical axis and vertical rotary shaft. Firstly， a mathematical model of geometric errors between optical axis and vertical rotary shaft was built based on geometrical optical principles， and influences of the tilt and translation between optical axis and vertical rotary shaft on measuring angle errors were analyzed. Then， a coaxiality detecting method based on the rotation imaging principle and image processing algorithm was proposed， and a set of coaxiality detecting device was designed. On the basis of the detecting device， the tilt and translation between optical axis and vertical rotary shaft were calibrated by adjustment of dual wedges. Results show that the angle error of optical axis and vertical rotary shaft is 3.4″ and the translation error is 26.1 μm after calibration， which meets the design indicator of femtosecond laser tracker. This work establishes a theoretical foundation for the subsequent system errors.

femtosecond laser tracker； coaxiality； rotation imaging； dual wedge； calibration

2016-06-17；

2016-08-02.

国家重大科学仪器设备开发专项资助项目(No.2011YQ120022)

1004-924X(2016)11-2651-07

TH249

10.3788/OPE.20162411.2651

*Correspondingauthor，E-mail：zhouweihu@aoe.ac.cn