电力电子系统可靠性模型综述

张 璇，耿嘉勇，曾德银，韩宗耀，魏涛涛，汪 鑫

（1.中国矿业大学信息与电气工程学院，徐州221116; 2.中国矿业大学孙越崎学院，徐州221116）

电力电子系统可靠性模型综述

张 璇1，耿嘉勇1，曾德银2，韩宗耀1，魏涛涛1，汪 鑫1

（1.中国矿业大学信息与电气工程学院，徐州221116; 2.中国矿业大学孙越崎学院，徐州221116）

近年来，电力电子装置广泛应用于生产生活各个领域中，其可靠性日益为人们所重视，尤其随着科学技术的飞速发展，可靠性研究也亟需与时俱进。可靠性关乎产品质量，其作为产品和设备安全性的评估指标不仅涉及企业、国家的经济效益，还涉及使用者的人身安全。首先主要介绍了电力电子系统级可靠性建模的主要开展方法、步骤及常见的可靠性建模方式，其可靠性建模主要有故障分析、失效判据选取、可靠性模型选取、建模和定量计算评估等主要步骤，故障分析是可靠性分析的基础，通过故障分析可以得到系统的主要故障类型，并基于所选取的失效判据判断系统在各故障类型下的运行状态；然后根据系统的规模、精度要求以及应用场合选取合适的可靠性模型有利于准确评估系统的可靠性，建模后进行定量计算，得到相应的可靠性指标，由此分析总结系统的可靠性；再介绍了4种常见的系统级可靠性模型，并依次对各模型进行了分析比较，总结了4种模型的特点与适用范围；最后对研究内容进行了总结与展望。

电力电子系统；系统级；可靠性模型；建模

引言

电力电子系统是以电力电子技术为核心，由电力电子器件组成的能够实现一定功能的整体［1］。随着电力电子技术的几次革新和机械化生产的快速发展，电力电子器件不断更新换代，使得电力电子系统趋于多功能与复杂化，更广泛地应用于能源、环境、交通运输、航空航天等重要领域。电力电子系统通常被用于生产工艺的关键流程中，是实现生产功能的重要部分。然而，电力电子系统在工作时其中的功率器件往往承受高电压、大电流以及极高开关频率，使其成为整个工作系统中最易发生故障的环节［2］。一旦出现故障，系统的运行效率会大大下降，甚至直接失效。因此，电力电子系统的稳定可靠运行与生产效率和质量有着直接联系，如何提高其可靠性、降低其故障率成为近年来的研究热点［3］。

提高电力电子系统可靠性的前提是对其进行准确的可靠性分析。可靠性是指产品在规定条件下、规定时间内实现其规定功能的能力，也可以将其定义为产品保持其规定功能的时间［4］。可靠性分析不仅需要结合产品的特性、应用场合进行，还需要严格设定故障指标用以判断产品是否失效。

可靠性工程最早可追溯至二战时期［5］，此后的二十年内，可靠性研究体系逐步形成、完善并开始了快速、全面的发展。1957年AGREE报告发布，其中描述了可靠性的定性分析方法和定量研究所需的基本数据，极大地促进了可靠性的进一步发展［6］。此后，可靠性在设计方法、建模方式、数据统计和故障分析等各个方面都趋于成熟，进入了全面发展阶段，与此同时，可靠性也开始逐渐被应用于各个领域中，与生产生活紧密结合。

可靠性不仅关乎产品质量，其作为产品和设备安全性的评估指标还涉及企业、国家的经济效益以及使用者的人身安全。近年来，国内外学者提出了多种可靠性建模方法，如可靠性框图RBD（reliability block diagram）模型、故障树分析FTA（fult tree analysis）模型等，其主要依靠分析系统中器件的失效率来计算系统的故障概率，从而估算出其可靠性。然而，早期提出的可靠性模型只能表征系统正常与故障两种状态，对评估的准确性造成限制。因此，提高可靠性模型精度以及提出能够表征系统状态转换过程、适应系统容错能力的可靠性模型成为当前的研究热点。

可靠性可分为元件级别与系统级别两部分［7］。元件级别主要针对电力电子器件，按经验数据或失效物理分析进行建模，计算出相应的可靠性指标，从而总结出其可靠性优劣［8-9］。系统级别的分析对象是由大量器件组成的设备或工作系统，通过不同方式对分析对象进行故障分析、建模并计算可靠性指标或参数，实现定性与定量的分析。本文主要研究系统级别的可靠性建模过程与方法，按分析过程展开介绍，主要分为可靠性指标的概念、产品故障分析与可靠性模型选取三部分内容。首先描述了常用可靠性指标的定义，并归纳出其计算方法与表达式。其次，对故障分析过程作了较为详细的介绍。通过故障分析可以总结出产品可能存在的所有故障类型，同时，结合选定的失效判据可以快速归纳出各故障模式下的运行状态，用以选定适用于该产品的可靠性模型及进行产品可靠性的定性分析。建立可靠性模型是可靠性分析的核心步骤，选定模型后，根据产品精度要求与结构特点、故障类型进行模型的适当简化，最后按模型的定量计算方法对产品进行可靠性评估。

1 可靠性指标

可靠性指标用于系统可靠性定量评估，一般常用有：失效率（failure rate）、可靠度（reliability）和故障前平均工作时间MTTF（mean time to failure）。

失效率是指在规定的时间之内失效产品的数量与产品总量的比值［10］，它可以用于表示某一个产品工作过程中在单位时间之内失效的概率，记为λ（t）。一般认为产品的失效率服从指数分布［11］，对于某种特定的器件，其在相同工作条件下的失效率往往近似为常值，由此简化了计算过程。

可靠度是指产品在规定的条件和规定的时间范围内完成其规定的功能的概率［12］。可靠度也可以类似表示为时间t的函数，记作R（t）。由失效率定义及指数分布方式可以得到可靠度表达式［11］为

失效前平均工作时间表示不考虑维修或不可修复的产品在未发生故障或未失效之前工作的平均时间［7］，根据可靠性定义可知，产品的可靠性可以由MTTF进行评估。其与可靠度的关系表示为

由可靠性定义，评估所得可靠度越大，则MTTF越大，表明产品保持其规定功能的时间越长，即产品可靠性越佳；反之，可靠度与MTTF越小，则产品可靠性越差。

2 产品故障分析

故障分析是整个可靠性分析过程中的基础，对指定产品进行全面深入的故障分析是保证可靠性研究过程准确性的第一步［12］。在故障分析过程中一般按照产品的组成分块进行总结，同时根据产品特性与用途决定故障分析时细分程度，对于精度要求低的产品或本身精密度很高的器件，可以考虑简化其故障分析结果，重点分析主要故障。

开关磁阻电机驱动系统，如图1所示。开关磁阻电机驱动系统是典型的电力电子系统，其主要由控制器、功率变换器、电机与检测器组成。对这四部分依次归纳总结可能存在的故障类型，可以基本得到驱动系统全部故障类型或故障模式。

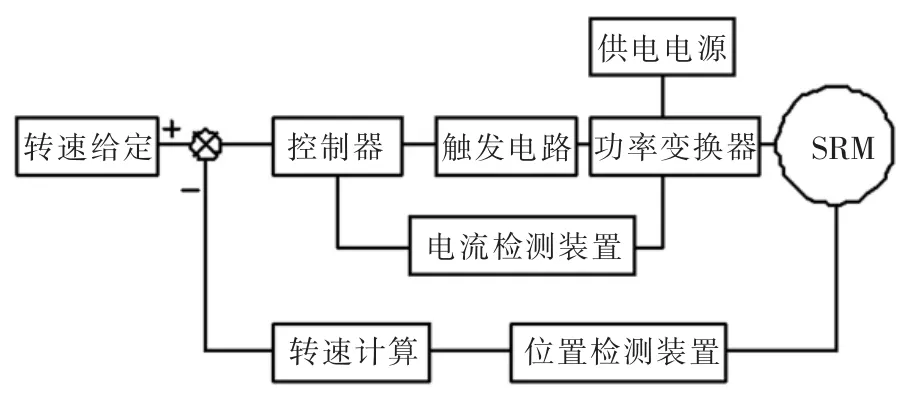
图1 开关磁阻电机驱动系统主要结构Fig.1 Structure of the switched reluctance motor drive system

在开关磁阻电机驱动系统中，由于控制器部分的核心部件为微处理器（常用DSP或FPGA等），这类芯片精密度高，工作中不涉及高电压或大电流，极少发生故障，可靠性高，因此往往不将其视为系统中的薄弱环节，可忽略此部分故障［13］；功率变换器部分包含大量开关器件，在系统运行时高频工作，承受电压大，易产生故障，因此对于功率变换器需要细分故障至每一个器件，一般有：开关管开路故障；开关管短路故障；直流母线电容开路故障；直流母线电容短路故障；二极管开路故障和二极管短路故障等，针对不同拓扑结构有时还将开关管和二极管按不同功能再进行故障类型细分［14］；与功率变换器类似，开关磁阻电机作为机电能量转换场所是系统中的重要组成部分，也需要细分故障类型，但其转子、主轴和轴承在工作时不接触电压与电流，其可靠性主要取决于生产工艺，在进行故障分析时一般不予考虑，只重点分析绕组故障模式；检测部分主要由位置和电流传感器器组成，一般故障模式为传感器的开路与短路故障。

然而，产品发生故障不一定导致其直接失效，还需进一步分析故障下产品工作状态，判断其是否能够实现规定的功能，以此总结出产品失效判据。

综上所述，在可靠性分析过程中，首先要根据产品的特性及应用场合具体要求进行故障分析并设置相应的故障指标，明确产品的失效判据，以便进行后续的建模与定量分析［15］。

3 系统级可靠性模型

对于系统级别的可靠性研究近年来国内外学者已经提出了多种分析方式，针对系统的可靠性建模方法有 RBD、FTA、Markov过程模型（Markov model）［10］和GO分析法［16］等。

模型可以分为静态模型和动态模型两大类。静态模型侧重于评估系统发生故障的概率，如RBD模型和FTA模型；动态模型则侧重于研究系统失效的过程以及多级故障对系统的影响，如GO法模型和Markov过程模型。

3.1 可靠性框图（RBD）模型

可靠性框图模型建模时将系统的各元件或子系统按框图形式表示，简洁直观表现系统的内部逻辑关系，建模快速，定量计算简单。该模型分为串联和并联两种，以开关磁阻电机驱动系统为例，二者的逻辑关系如图2所示［17］，其中，图（a）为开关磁阻电机驱动系统简化后得到的串联可靠性框图模型，图（b）为功率变换器部分桥臂间的并联模型。

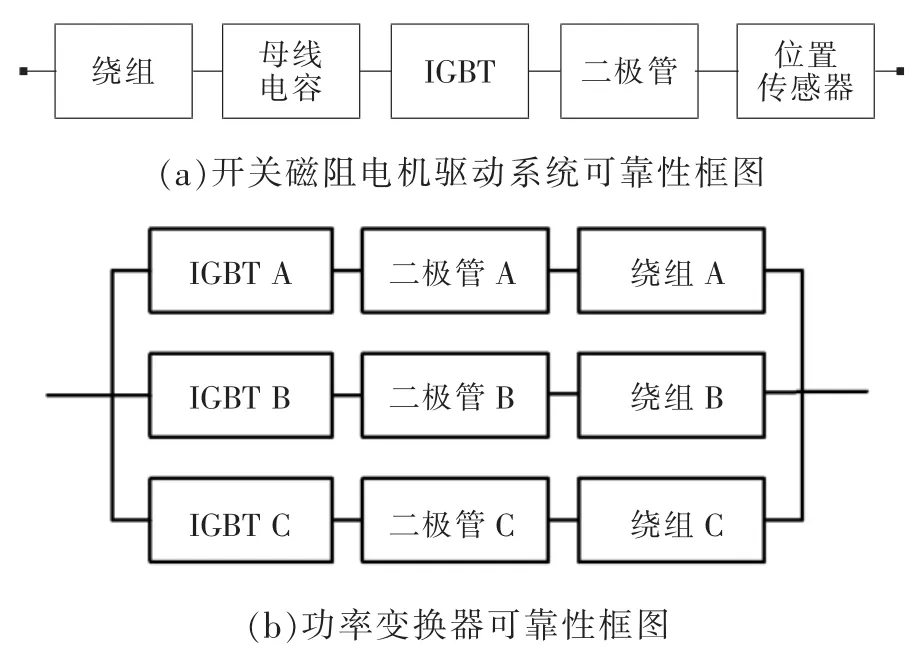
图2 RBD串联系统与并联系统逻辑关系示意Fig.2 Series and parallel connection of RBD model

模型中各器件的失效率计算公式为

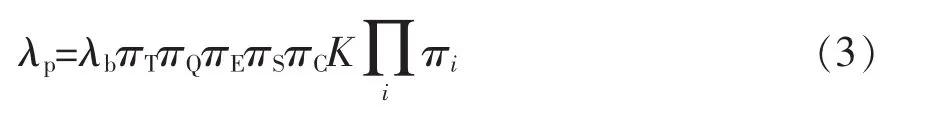
式中：λb为器件的基本失效率；K为修正系数；πT、πQ、πE、πS及πC分别为温度、质量、环境、电应力以及结构失效系数，以上系数均可通过查找可靠性预计手册得到相应取值。目前应用最广泛的可靠性预计手册为美国的电子设备可靠性预计手册MILHDBK-217F和国内的《电子设备可靠性预计手册》（GJB/Z 299C-2006）。

根据可靠性预计手册提供的可靠性框图模型定量评估计算公式，串联系统的总失效率为各个元件的失效率乘积，并联系统的总失效率为各个元件的失效率相加和。计算得出系统总失效率后，可由式（1）和式（2）计算出系统的可靠度和MTTF。

可靠性框图模型由于其建模快速和计算简单的优点被广泛应用于小型简单系统的可靠性分析或复杂系统的初步可靠性评估。小型简单系统如电子仪器或电力系统，多用可靠性框图模型进行简单的可靠性分析，从而评估系统性能，文献［18］对电子测压器的可靠性展开了研究，将其按组成结构细化，采用串联模式的可靠性框图模型进行分析与计算，得到测试系统的总失效率与故障前平均工作时间，并与实验结果进行对比分析，证明可靠性框图模型的评估结果；文献［19］针对智能变电站的继电保护装置进行了可靠性分析，采用可靠性框图模型，得到较为准确的评估结果。复杂系统多为用于实际工业生产、交通或航空航天领域的大型系统，如文献［20-21］分别对动车组高压电气系统和石油井下压力测试系统进行了快速建模，利用可靠性框图模型初步分析并计算得到评估指标，从而判断系统能否实现预期功能。但该建模方法无法表征系统多级故障运行状态，即系统带故障运行状态，因此只适用于定量评估要求低或无容错能力的系统的可靠性分析。

3.2 故障树分析（FTA）模型

故障树分析模型是一种通过树形结构表示系统故障与各个组成部分故障间逻辑关系的可靠性模型。故障树模型一般由顶事件、中间事件以及底事件组成，通过树形模型可以尽可能地找出所有导致顶事件（一般为“系统故障或失效”）发生的底事件（一般表示最底层元器件或其他组成部分的故障或失效）。故障树分析模型由事件和逻辑门结构组成，分析方式自上而下，既可以用于定性分析，又可以用于定量计算。故障树分析模型有与门逻辑和或门逻辑两种基本结构，以开关磁阻电机为例［17］，如图3所示。

图中X1，X2，…，Xn为底事件，顶事件用字母T表示。或门表示下层任意一种故障的发生都会导致顶事件发生，与门表示需下层所有事件同时发生，顶事件才会发生。根据可靠性预计手册提供的定量计算方法，顶事件发生的概率可表示为

故障树分析模型计算得出的概率等价于可靠性指标中的失效率，其后续定量评估方法与可靠性框图模型计算一致，通过可靠性指标计算公式得到可靠度与MTTF。

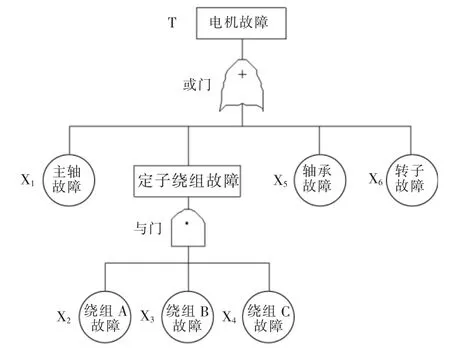
图3 故障树分析与门逻辑结构与或门逻辑结构示意图Fig.3 Structure of the and gate and the or gate of FTA model

故障树分析模型可以直观表示出系统故障与各部分器件故障之间的逻辑关系，还可以定量计算出系统的故障概率，具有结构清晰、求解简单的优点，工业生产中常用于电力电子系统可靠性分析、潜油电机可靠性以及核电站循环水泵电机轴承烧瓦问题等领域。文献［22］详细介绍了潜油电机故障树分析模型的建立与分析方法，并基于VC++开发环境建立了基于故障树的潜油电机故障诊断系统，从而提高了故障诊断的效率；文献［23］采用故障树分析模型对核电站循环水泵电机轴承烧瓦问题进行研究，从定性角度分析了故障树结构的重要度，找到了易引起故障的环节，并以此为指导重点处理优化了故障环节，解决了烧瓦问题，同时对薄弱环节进行了总结，有利于故障的预防。但故障树分析模型为静态模型，不具有分析系统带故障运行状态的能力，应用范围受到一定的限制。

可靠性框图与故障树分析作为静态可靠性分析模型，二者建模原理类似，可相互转化且定量计算结果基本一致，同时具有建模快速、结构清晰、模型直观和计算简单的优点，但都无法表示系统带故障运行能力的缺陷，因此二者适用范围基本相同。

3.3 GO分析模型

GO法是一种以成功为导向的系统级可靠性分析方法［24-25］，其以操作符为单元，以信号流为单元之间的连接，通过建立GO模型图将系统的工作过程或内部逻辑直观展示出来。GO法的最大特点是可以直接进行定量计算得到精确结果，省去了传统可靠性分析方法中故障定性分析的步骤。其由输入操作符开始，按照不同操作符的运算规则沿信号流逐步计算，得到系统最终输出信号的状态概率［16］，其中最大的误差来源是共有信号的状态概率计算。若某信号流同时输入至多个操作符，则将其称为共有信号流。GO法的原始算法为基于信号流状态联合概率计算［25］，当存在共有信号时，其结果往往是复杂的多个信号流状态组合的概率，不能直接得到各个信号流的状态概率［16］。随着GO法的发展与优化，定量计算新算法及操作符计算公式［26］和共有信号计算法［27］等新算法弥补了原始算法的不足，使评估结果更精确，同时也能够适应较复杂的系统。以含一个共有信号的电力系统为例，如图4所示。

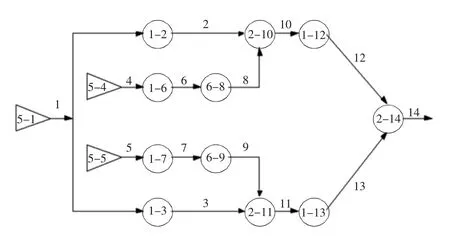
图4 含一个共有信号系统GO图Fig.4 GO model of the system with one shared signal

GO图中操作符内前一位数字表示操作符类型，常见操作符类型有17种［26］；后一位数字表示操作符编号；连接线上的数字表示信号流编号。图4中有4种不同形式的操作符，分别为“两状态单元”（图中类型1）、“或门”（图中类型2）、“信号发生器”（图中类型5）和“有信号而导通的元件”（图中类型6）。以PSi表示状态值为i的信号流成功的概率，以PRi表示状态值为i的操作符成功的概率。根据图4可以对各部分状态概率进行定量计算，得到系统的成功概率为

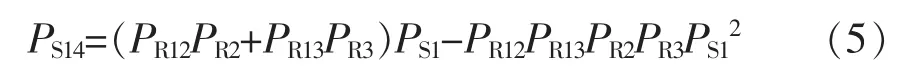
由于系统中只含有一个共有信号，因此系统状态概率方程将含有共有信号的2次项；当系统存在多个共有信号时，将出现共有信号的高次项。修正时采用一次项代替高次项，对方程进行简化，同时修正了共有信号项［16］，得到正确的表达式，即

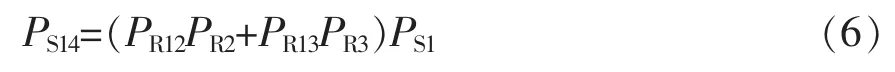
当系统存在多个共有信号时，系数计算复杂，一般采用编程方式进行处理以快速得到计算结果。

目前GO法多用于供电系统的可靠性分析，文献［28］将GO法引入配电网可靠性评估中，在考虑转移负荷影响的情况下建立了带分支支路的复杂配电网络GO模型，计算并评估了系统的可靠性，并以IEEE RETS算例进行了验证，最终证明GO法适用于复杂的配电网络的可靠性评估分析。

由以上分析可知，GO法具有可直接进行定量计算，评估结果精确且能够表征系统多级故障工作状态的优点，但由于其模型计算的复杂性，使得该模型不适合过于复杂的系统。

3.4 Markov过程模型

Markov过程模型分析是一种动态建模方法，认为当系统当前状态已知时，其未来状态的转化发展与其过去状态无关［29］，由此可将系统状态分为正常、存活和失效3种状态［17］，其中，正常状态指系统所有的性能指标都在正常范围内，系统内无故障发生；存活状态指系统中出现故障但不至于失效，系统可以继续带故障运行，各项性能指标仍在正常范围之内；失效状态指系统发生故障导致系统无法继续运行或存在性能指标不正常的情况。将正常运行的系统发生的任意一种故障定义为一级故障，此后若系统直接失效则不再叠加故障进行分析，若存活则需再叠加一种故障，称为二次故障，以此类推直至系统失效。由此可以得到多个系统存活与失效状态组合。同一种器件不能存在两种不同状态，即若一级故障时该器件已失效，则其无法再发生二级故障。为简化分析过程，防止状态爆炸，一般认为任意三级故障发生后系统必定失效，同时，三级故障模型分析可以基本保证模型的准确性［14］。

确定状态转换过程与状态转换概率是Markov模型定量分析的基础，通过故障分析总结出系统故障类型后按一级、二级、三级故障依次进行归纳，并列出各故障下系统的状态，由此得到系统状态转换过程。状态转换概率一般采用导致系统状态转换的各故障或失效组合的失效率，其值可通过查阅可靠性预计手册得到。确定状态转换过程与转换概率后即可得到系统状态转换图，剔除失效组合后得到状态转换概率矩阵Φ*n×n，其中n为系统状态数。利用Markov理论中求解系统状态概率的Chapman-Kolmogorov微分方程［30］和状态概率矩阵Φ*n×n求得系统存活状态概率矩阵P*（t）。Chapman-Kolmogorov方程描述了某时刻t系统状态的概率，可表示为

通过解此微分方程可以得到从系统某个状态转换至另一个状态的概率，每个状态概率都是时间t的函数。则式（4）的解［14］可表示为

式中，PT（0）为系统在最初时刻各种状态的概率，除系统正常状态N的初始状态概率为1外，其余各状态的初始概率均为0。将P*（t）中各元素相加即可求出基于Markov模型的可靠度函数R（t），最终可求得MTTF以定量评估系统的可靠性。

以开关磁阻电机公共开关式功率变换器为例，其Markov模型如图5所示，其拓拟结构如图5（a）所示。根据Markov模型建模方法构建其状态转换模型如图5（b）所示。图中S和Sn（n=1，2，3，4）表示MOSFET，VD和VDn表示二极管，A～D为4相绕组；N表示系统正常运行状态，A1、A2、B1、B2表示系统存活状态（即带故障运行状态），F表示系统失效状态，各状态之间λ表示状态转换概率。通过建立Markov模型可以清晰表示出系统状态之间的转换关系，同时由转换概率可求得系统的可靠性指标，能够充分表征系统带故障运行能力，有利于对系统的可靠性进行准确全面的评估。但Markov模型的建立必须有严格的失效判据和全面故障分析，在不限定故障级数情况下对于大型或复杂系统，模型中的状态数极多，数据难以处理［8］。因此在实际建模过程中往往对故障级数进行限制或简化，使模型不致过于复杂，但在一定程度上降低了模型的精确性。

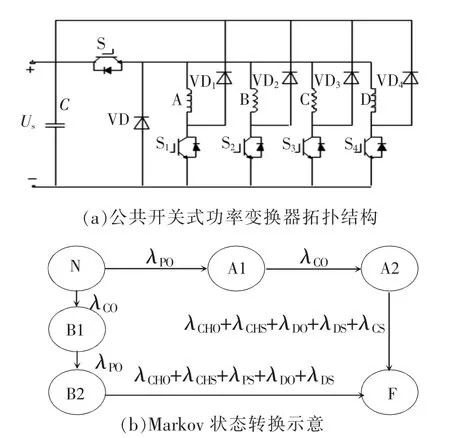
图5 公共开关式功率变换器Markov模型Fig.5 Markov model of the public switch type power converter

Markov模型由于其高精度的定量评估和对系统多级故障状态的充分表征被广泛应用于高压输电线继电保护装置风险评估等领域。文献［31］根据高压输电线继电保护自检特性，提出了保护装置引发的四种风险，通过对系统的十种状态建立Markov模型，利用模型给出各风险指标计算方法，基于电网实测数据对比了可靠性评估准确性。由此证明，Markov模型能够准确评估多级、复杂系统可靠性。

3.5 静态、动态模型特点总结

将前述4种模型进行比较，结果如表1所示。

表1 系统级可靠性模型对比Tab.1 Contrast of system-level electronic systems models

由表可见，静态模型建模原理简单，结构简洁清晰，计算量小，可实现快速建模，能表征系统故障与正常状态；但不具表征系统带故障运行状态的能力，精确度低，不适合具有容错能力的系统及复杂、要求定量评估精度高的系统。

动态模型原理较复杂，模型结构清晰，能够体现系统运行状态或状态转换过程，可表征系统带故障运行状态，定量评估精确度高；但其计算量大，不适合过于复杂的系统，如需应用于复杂系统，则需进行适当的简化。

4 结语

本文主要介绍了电力电子系统级别可靠性分析的基本概念、开展方法及建模主要步骤，重点分析了常见系统级可靠性建模方法，并对静态与动态模型进行比较与总结。其中阐述了近年来新引入的GO分析法，具体分析了该建模方式的优缺点，结合案例进行定量计算及结果修正。以上分析方法均适用于常见的电力电子系统，如电机驱动系统、电力电子变换器等。通过对可靠性建模、定性分析与定量计算，能够充分表征系统故障类型与故障间逻辑关系，得出系统各项可靠性指标，为系统寿命的评估提供了可靠依据；同时，能够找出系统组成中的薄弱环节，据此可以对系统进行有针对性的优化与改善，提高系统整体性能。本文对4种建模方法进行了归纳总结，可根据其各自特点，结合实际系统选择一种或多种模型，对系统可靠性进行全面分析，得到所需精确度的评估结果。

本文介绍的建模方法及其计算均以器件失效或故障概率为基础，模型定量评估结果的精确性不仅取决于模型本身的精确程度，还取决于各器件故障概率的准确性，这也是现今可靠性模型精度提高面临的最大难点。因此本文总结的模型特点与精度比较需以器件故障概率准确性一致为前提。未来可靠性模型的精度提高一方面需要对可靠性预计手册中器件的失效率进行实时更新，还需要新的建模方法的提出，减少对可靠性预计手册的依赖，同时进一步改善模型对系统状态转换过程的描述，提高模型的普适能力。

［1］钱照明，张军明，盛况.电力电子器件及其应用的现状和发展［J］.中国电机工程学报，2014，34（29）:5149-5161.Qian Zhaoming,Zhang Junming,Sheng Kuang.Status and development of power semiconductor devices and its applications［J］.Proceedings of the CSEE,2014,34（29）:5149-5161（in Chinese）.

［2］周雒维，吴军科，杜雄，等.功率变流器的可靠性研究现状及展望［J］.电源学报，2013，11（1）:1-15.Zhou Luowei,Wu Junke,Du Xiong,et al.Status and outlook of power converter’s reliability research［J］.Journal of Power Supply,2013,11（1）:1-15（in Chinese）.

［3］蔡涛，段善旭，康勇.电力电子系统故障诊断技术研究综述 ［J］.电测与仪表，2008，45（509）:1-7,48.Cai Tao,Duan Shanxu,Kang Yong.A survey of fault diagnosis technology for power electronics system［J］.Electrical Measurement&Instrumentation,2008,45（509）:1-7, 48（in Chinese）.

［4］郭永基.可靠性工程原理［M］.2版.北京：清华大学出版社，2002.

［5］Coppola A.Reliability engineering of electronic equipment a historical perspective［J］.IEEE Transactions on Reliability,1984,33（1）:29-35.

［6］Denson W.The history of reliability prediction［J］.IEEE Transactions on Reliability,1998,47（3）:SP321-SP328.

［7］章国栋.系统可靠性与维修性的分析与设计［M］.北京：北京航空航天大学出版社，1990.

［8］徐帅，杨欢，王田刚，等.电力电子变换器可靠性研究［J］.北京交通大学学报，2015，39（5）:125-132.Xu Shuai,Yang Huan,Wang Tiangang,et al.Research on reliability of power electronic converter［J］.Journal of Beijing Jiaotong University,2015,39（5）:125-132（in Chinese）.

［9］丘东元，刘玉飞，张波.基于加权网络模型的电力电子电路可靠性分析［J］.电源学报，2014，12（3）:58-63.Qiu Dongyuan,Liu Yufei,Zhang Bo.Reliability analysis of power electronic circuits based on the weighted network model［J］.Journal of Power Supply,2014,12（3）:58-63（in Chinese）.

［10］Military Handbook Reliability Prediction of Electronic E-quipment:MIL-HDBK-217F［S］.US Department of Defense, 1995.

［11］Military Handbook Electronic Reliability Design Handbook:MIL-HDBK-338B［S］.US Department of Defense,1998.

［12］Chen Hao,Yang Huan,Chen Yuxiang,et al.Reliability assessment of switched reluctance motor drive under single switch chopping strategy［J］.IEEE Transactions on Power Electronics,2016,31（3）:2395-2408.

［13］陈玉香.开关磁阻电机系统可靠性研究［D］.徐州：中国矿业大学，2014.Chen Yuxiang.Study on reliability of switched reluctance motor system［D］.Xuzhou:China University of Mining and Technology,2014（in Chinese）.

［14］卢胜利，陈昊，昝小舒.开关磁阻电机功率变换器的故障诊断与容错策略 ［J］.电工技术学报，2009，24（11）:199-206.Lu Shengli,Chen Hao,Zan Xiaoshu.Fault diagnosis and faulttolerantcontrolstrategy for powerconverterof switched reluctance motor［J］.Transactions of China Electrotechnical Society,2009,24（11）:199-206（in Chinese）.

［15］赵文祥，程明，朱孝勇，等.驱动用微特电机及其控制系统的可靠性技术研究综述［J］.电工技术学报，2007，22（4）:38-46.Zhao Wenxiang,Cheng Ming,Zhu Xiaoyong,et al.An overview of reliability of drive system for small and special electric machines［J］.Transactions of China Electrotechnical Society,2007,22（4）:38-46（in Chinese）.

［16］沈祖培，郑涛.复杂系统可靠性的GO法精确算法［J］.清华大学学报，2002，42（5）:569-572.Shen Zupei,Zheng Tao.Exact algorithm for complex system reliability using the GO methodology［J］.Journal of Tsinghua University,2002,42（5）:569-572（in Chinese）.

［17］杨欢.开关磁阻电机驱动系统可靠性研究［D］.徐州：中国矿业大学，2015.Yang Huan.Study on reliability of switched reluctance drive［D］.Xuzhou:China University of Mining and Technology,2015（in Chinese）.

［18］卢彦玲，李新娥，王亚军.可靠性框图在电子测压器可靠性分析中的应用［J］.探测与控制学报，2013，35（4）:44-48.Lu Yanling,Li Xine,Wang Yajun.Reliability block diagram applied in electronic pressure gauge reliability analysis［J］.Journal of Detection&Control,2013,35（4）:44-48（in Chinese）.

［19］谷磊.智能变电站继电保护可靠性研究［D］.广州：广东工业大学，2014.Gu Lei.The research on reliability of smart substation relay protection system［D］.Guangzhou:Guangdong University of Technology,2014（in Chinese）.

［20］刘建强，崔秀国，孙帮成,等.CRH3型动车组高压电器系统可靠性研究［J］.铁道学报，2013，35（6）:22-27.Liu Jianqiang,Cui Xiuguo,Sun Bangcheng,et al.Research on reliability of high voltage apparatus system of CRH3electric multiple units［J］.Journal of the China Railway Society,2013,35（6）:22-27（in Chinese）.

［21］郝鑫刚，李新娥，崔春生,等.油井压力测试系统可靠性框图分析［J］.传感技术学报，2016，29（1）:64-68.Hao Xingang,Li Xine,Cui Chunsheng,et al.Reliability block diagram analysis on pressure test system of oil-well［J］.Chinese Journal of Sensors and Actuators,2016,29（1）:64-68（in Chinese）.

［22］尹松，冯定，聂家强,等.基于故障树的潜油电机故障诊断系统的建立［J］.现代机械，2006（5）:30-36.Yin Song,Feng Ding,Nie Jiaqiang,et al.The foundation of the electric submersible motor fault diagnosing system based on fault tree［J］.Modern Machinery,2006（5）:30-36（in Chinese）.

［23］李力，郭猛，韩垂煌,等.基于故障树的核电站循环水泵电机烧瓦问题研究［J］.机电工程，2015，32（9）:1246-1262.Li Li,Guo Meng,Han Chuihuang,et al.Bush-burning study on circulating pump motor of nuclear power station based on fault tree［J］.Journal of Mechanical&Electrical Engineering,2015,32（9）:1246-1262（in Chinese）.

［24］Williams R L,Gateley W Y.Use of GO methodology to directly generate minimal cut set［A］.Pennsylvania Society for Industrial and Applied Mathematics,1977.

［25］Chu B B.Overview manual GO methodology［R］.EPRI NP-3123 1.Washington Electric Power Research Institute, 1983.

［26］沈祖培，高佳.GO法原理和改进的定量分析方法［J］.清华大学学报，1999，39（6）:15-19.Shen Zupei,Gao Jia.GO methodology and improve quantification of system reliability［J］.Journal of Tsinghua University,1999,39（6）:15-19（in Chinese）.

［27］Shen Zupei,Gao Jia,Huang Xiangrui.A new quantification algorithm for the GO methodology［J］.Reliability Engineering and System Safety,2000,67（3）:241-247.

［28］徐荆州，李扬.基于GO法的复杂配电系统可靠性评估［J］.电工技术学报，2007，22（1）:149-153.Xu Jingzhou,Li Yang.Reliability assessment of complex distribution system using GO method［J］.Transactions of China Electronical Society,2007,22（1）:149-153（in Chinese）.

［29］Chan F,Calleja H.Reliability estimation of three singlephase topologies in grid-connected PV system［J］.IEEE Transactions on Industrial Electronics,2011,58（7）:2683-2689.

［30］朱显辉，师楠，田德文,等.PWM驱动电机可靠性研究发展及展望［J］.哈尔滨理工大学学报，2014，19（4）:22-31.Zhu Xianhui,Shi Nan,Tian Dewen,et al.The development and prospect of reliability research on PWM-Driving motor［J］.Journal of Harbin University of Science and Technology,2014,19（4）:22-31（in Chinese）.

［31］薛安成，罗麟，景琦,等.基于Markov模型的高压输电线继电保护装置风险评估［J］.电网技术，2014，38（7）:1995-2000.Xue Ancheng,Luo Lin,Jing Qi,et al.Research on markov model based risk assessment of protective relaying for voltage transmission line［J］.Power System Technology,2014, 38（7）:1995-2000（in Chinese）.

An Overview of Reliability for Power Electronic Systems

ZHANG Xuan1,GENG Jiayong1,ZENG Deyin2,HAN Zongyao1,WEI Taotao1,WANG Xin1
（1.School of Information and Electrical Engineering,China University of Mining and Technology,Xuzhou 221116, China;2.Sun Yueqi Honors College,China University of Mining and Technology,Xuzhou 221116,China）

In recent years,power electronic products have been widely used in the industrial production and everyday life,and the reliability has been paid more and more attention.Research of the reliability was expected to develop as well,especially with the fast development of the science and technology.It is not only about the quality,but also about the enterprises and nation’s economic benefit and users’safety since it is an assessment index of products’safety.This paper mainly introduces the method of carrying out modeling of the system-evel reliability of power electronic systems,the modeling steps and the models that are often used to analyze products’reliability.The main steps are fault analysis,choosing failure criteria,choosing reliability models and quantitative calculation and assessment.Fault analysis is the basis of reliability analysis.By fault analysis,the main fault types of the system can be obtained and the condition of the system under faults on the basic of failure criteria can be estimate.Choosing suitable models according to the scale,accuracy requirement and applications of the system helps to get accurate assessment results.Assessment index can be calculated after modeling to analyze and summarize the reliability of systems.Four usual models of systemlevel reliability are introduced in this paper and the characteristics and applications of them are summarized.Finally,the article summarizes the main work and the deficiencies,and gives some prospects.

power electronic system;system-level;reliability model;modeling

张璇

张璇（1994-），女，通信作者，博士研究生，研究方向：电力电子与电力传动，E-mail：joana__z@126.com。

耿嘉勇（1994-），男，本科，研究方向：电气工程及其自动化，E-mail：13952202553@163.com。

曾德银（1994-），男，本科，研究方向：电气工程及其自动化，E-mail：04131800@cumt.edu.cn。

韩宗耀（1994-），男，本科，研究方向：电力系统及其自动化，E-mail：913562671@qq.com。

魏涛涛（1994-），男，本科，研究方向：电气工程及其自动化，E-mail：15505168742@163.com。

汪鑫（1995-），男，本科，研究方向：电气工程及其自动化，E-mail：625661800@qq.com。

10.13234/j.issn.2095-2805.2016.6.99

TM 464

A

2016-08-02

江苏省2016年度普通高校研究生科研创新计划资助项目（KYLX16_0530，KYLX16_0528）；江苏省高等学校大学生创新创业训练计划资助项目（07150023）；中国矿业大学大学生创新创业训练计划资助项目（04160014）

Project Supported by Jiangsu Ordinary University Graduate Research and Innovation Project for 2016（KYLX16_0530，KYLX16_0528）;Jiangsu Students’ Innovation and Entrepreneurship Training Program（07150023）;China University of Mining and Technology Students’Innovation and Entrepreneurship Training Program（04160014）