功率MOSFET寿命模型综述

查晓明，刘悦遐，黄 萌，刘 懿

（武汉大学电气工程学院，武汉430072）

功率MOSFET寿命模型综述

查晓明，刘悦遐，黄 萌，刘 懿

（武汉大学电气工程学院，武汉430072）

MOSFET是实现电力电子装置功能的核心器件，但其寿命短是制约电力电子系统可靠性的关键因素。由老化造成的MOSFET失效分为封装失效和参数漂移失效，前者由MOSFET制造工艺及材料导致的缺陷在工作环境中恶化而产生，后者为器件在使用过程中其内部微观退化机制在宏观参数的体现。对目前已有的MOSFET寿命相关的研究成果进行总结，分析了MOSFET的各类失效模式，并建立了各类失效模式下MOSFET寿命模型；并进一步总结了各类失效模式下寿命模型的失效判据及其各类寿命预测模型实验验证方法。

MOSFET；寿命模型；封装失效；参数漂移失效

引言

金属-氧化物半导体场效应晶体管MOSFET（metal-oxide-semiconductor field-effect transistor）具有电阻低、驱动耗散功率小等特点，其高频特性更是满足了逆变器的需求，在中小功率等级电能转换被广泛应用，是实现电力电子装置基本功能的核心器件［1］。SiC技术的出现进一步扩展了MOSFET的应用范围［2-3］。因此，相比其他器件，MOSFET在电力电子装置中占据重要地位。研究表明功率开关器件的老化失效导致电力电子系统故障的比例高达34%，其寿命严重限制了整个电力电子系统的可靠性［4-6］。功率MOSFET的老化失效会恶化电力电子装置的输出电能质量，甚至危害整个系统的安全运行［7］。因此，分析MOSFET失效机理，建立其寿命模型具有重要意义。

MOSFET的老化失效可大致分为两类：封装失效和参数漂移失效［8］。封装失效是指器件在制造过程中受外界环境（温度、湿度等）、制作原材料的影响造成器件内部结构的缺陷（黏结层空洞等），该缺陷在器件使用过程中逐渐恶化，最终导致MOSFET封装失效。这类失效会造成器件芯片缓慢热击穿、键合引线反复弯折断裂、黏结层循环疲劳等，因而对MOSFET器件内部易损坏部位的温度、应力进行预测，判断其是否达到击穿/断裂的临界值是建立MOSFET封装失效寿命模型的典型方法［9-15］。

另外，工业应用对器件功率密度要求逐渐提高，MOSFET尺寸在不断减小，其栅氧化层也随之变薄，然而电源电压因电源兼容性的问题无法采用恒场率（CE）等比例缩小，在横、纵向电场应力下，沟道热载流子注入、高压偏置以及栅氧化层经时击穿等问题显著上升［16］。这些问题到界面态的数量上升进一步造成MOSFET的参数漂移失效。目前MOSFET参数漂移失效的寿命模型建模方法均为基于MOSFET失效机理的寿命预测模型，如热载流子失效HCI（hot carrier injection）寿命模型［17-19］、栅氧化层经时击穿TDDB（time dependent dielectric breakdown）寿命模型［20-22］以及负偏压不稳定性NBTI（negative bias temperature instability）寿命模型［23-25］等。

本文对MOSFET的失效模式进行了总结分类，在此基础上对封装失效与参数漂移失效的原因以及各类失效机理产生的原因及其导致造成的影响进行了分析，对各类寿命模型进行了总结，并给出了各类失效模式下对应的寿命预测模型，为不同条件下的MOSFET应用以及提高MOSFET可靠性提供了参考依据。

1 MOSFET失效模式及其原理分析

MOSFET失效模式是指器件失效时的外在直观失效表现形式及过程规律，通常指测试或观察到的失效现象和失效形式［26］，表现为参数漂移、器件击穿或烧毁、器件裂纹扩展、粘结不良等。MOSFET具体失效模式之间的关系如图1所示，2种模式往往在器件的使用过程中同时产生。

图1 MOSFET失效模式关系Fig.1 Relationship of MOSFET failure mode

1.1 封装结构失效模式

典型的封装结构失效分为芯片热击穿、黏结层疲劳、键合引线断裂及塑料封装外壳失效等。器件的失效一般发生在制造、储存、运输以及使用过程中，器件在制造过程中的外界环境（温度、湿度等）、制作原料以及器件的工作环境与封装失效的发生有着密切关系［27］。表1为典型封装失效与环境因素的关系［28］，表中符号代表含量义如下：① 过应力型失效模式：A脆性断裂失效，B介质屈服，C塑性失效，Q弹性形变，E胶质脱落，X EOS/ESD，AM过热应力击穿，AN二次击穿。②耗损型失效模式：J腐蚀，K晶体过大，M渗透扩散，L疲劳裂纹深度增加，R疲劳裂纹出现，T电迁移，Z金属材料迁移，U氧化层失效，AD TDDB击穿。

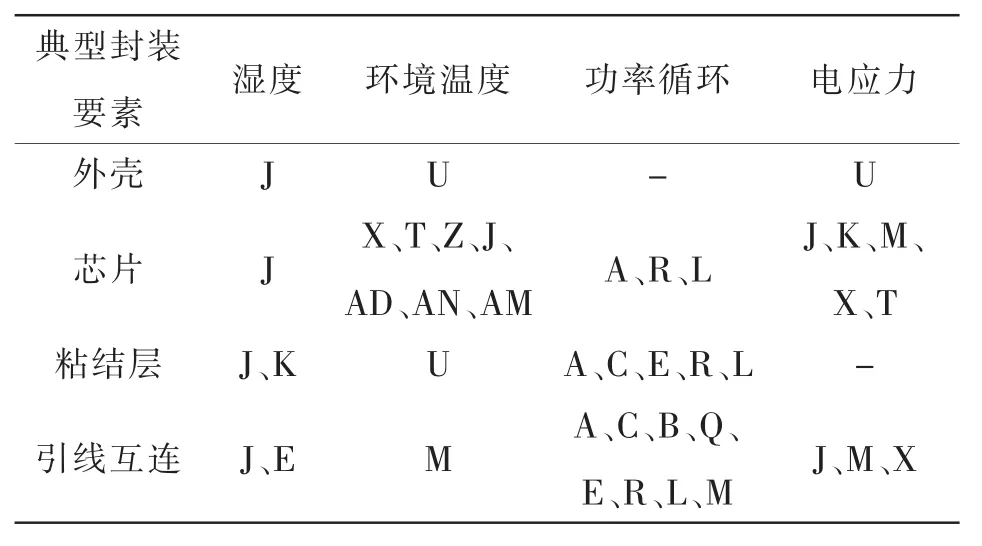
表1 典型封装失效模式与环境因素的关系Tab.1 Relationship between typical package failure modes and environmental factors

图2给出了MOSFET的封装结构。

图2 MOSFET封装结构Fig.2 Package structure of MOSFET

1.1.1 芯片热击穿失效

芯片击穿是指芯片在热应力作用下导致的某一对或某一组输入输出引脚之间完全呈现导通状态。相比于电击穿，芯片的热击穿一般不可恢复，芯片热击穿后其逻辑功能将不再正常，通常表现为短路状态。

器件黏结层内存在大小不一的空洞，影响热传递，从而影响器件各部分的热阻，这将对芯片在工作过程中的散热产生干扰，从而产生局部热点导致芯片的热击穿。造成芯片热击穿现象可以用热场耦合的方法进行分析，当实际结温高于最高允许温度时认为发生热击穿现象，分析模型为

式中：Tjunc，allοw为芯片结温最大值，℃；Tjunc为某环境应力下的结温，℃。MOSFET内部的实际结温由器件的等效热阻 Rth，i（℃/W）、器件的能耗功率 Qd（W）、耗散功率、环境温度在最高水平下的平均值Tamb，max（℃）共同决定，即

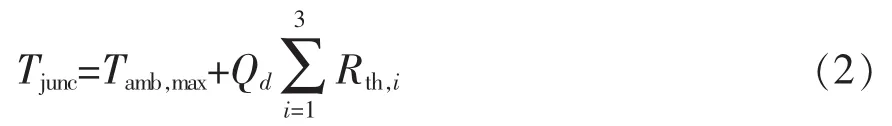
芯片等结构的等效热阻值Rth，i取决于其热导率、尺寸以及边界条件，即

式中：Ki为单层热导率，W/（m·K）；li为单层长度，m；wi为单层宽度，m；ti为单层厚度，m。

1.1.2 黏结层疲劳失效

黏结层疲劳是指器件的芯片在温度循环的作用下受到封装与键合引线的热应力，导致芯片与黏结层之间产生裂纹并最终剥离。当黏结层疲劳失效后，黏结层与芯片的剥离将导致MOSFET导电、导热通道受损，MOSFET表现为高阻或开路状态。

MOSFET的外壳、黏结层、芯片等由于材料的不同导致其在使用过程中温度也存在差异，其中芯片及基板之间的热膨胀系数相差较大，在热应力的作用下两者间的黏结层更易发生疲劳失效。芯片及黏结层之间的界面应力符合 Bolger方程，结合Coffin-Manson方程，预测黏结层疲劳失效之前的工作的次数［29］为

式中：Δγp，att为芯片粘结层发生塑性应变的上下限；ccf为疲劳韧性指数；εcf为疲劳延展性系数；Nf达到失效阈值时的次数。

1.1.3 键合引线断裂失效

键合引线断裂是指器件的键合引线在温度循环的热应力下反复压缩拉伸，导致其金属疲劳最后断裂。键合引线断裂后MOSFET表现为高阻或开路的形式。

由于键合互联的引线及其连接部分的热膨胀系数不同，键合引线在温度循环下易发生疲劳失效。在温度循环下，引线的伸缩与稳态温度无关［15］，设其温度变化幅值为ΔT（℃）、引线长度为2L（m）、引线宽度为2D（m），键合互连引线在热膨胀作用下引起的弯曲应力可以通过模型描述为引线纵横比的函数，其根部应力可表示为

式中：ΔT为工作期间的温度循环变化；Ewr为引线弹性模量，Pa；αwr为引线的热膨胀系数，℃；αsub为衬底的热膨胀系数，℃-1。则器件的估计工作寿命［30］为

1.1.4 塑料封装外壳失效

塑料封装外壳失效是指由于封装材料的吸湿性，导致材料膨胀变形及水分蒸发后蒸汽压力导致的塑封材料与芯片的分层效应，最终导致键合引线的断裂。塑料封装外壳失效后MOSFET表现为开路特性。

电子器件封装中最常用的塑料材料为环氧树脂，其具有易于吸湿的特点［31］，而器件中其他材料的吸湿能力各不相同。当器件工作于湿热环境下时不同材料之间将产生不同的热应力与膨胀应力，同时材料吸收的湿气在高温下的蒸发形成压强引起裂纹。温度升高到Telev使最大弯曲应力σmax，mc超过破裂应力阈值时，就会产生裂纹，其数学表达式为

芯片焊区长边的中心最先达到最大值，即

式中：σcrit，mc为临界应力，是固化时的最大弯曲应力，Pa；Kf为应力强度因子（正方形焊区Kf=0.05）；adie为芯片的宽度，m；tmc为包封塑料的厚度，m；Pc为封装内的蒸汽压，Pa；Psat，elev为高温下的饱和压强，Pa；RHsat为温度冲击前环境的相对湿度。

1.1.5 失效模式之间的相互影响

作为连接器件芯片与基板的黏结层，其良好的导热性不仅能帮助芯片散热，同时还能吸收芯片和引线框架之间的热失配而产生的机械应力［15］，黏结层的裂纹、空洞等必然会导致芯片的热失效以及热退化现象等问题，而芯片温度的升高将进一步加剧黏结层的疲劳失效；塑料封装外壳包封整个器件，当其受到蒸汽应力、热应力等产生裂纹时，器件的键合引线以及芯片同样会受到应力的作用而导致裂纹的产生，芯片裂纹导致其温度上升进而影响塑封外壳受到的热应力与膨胀应力等，加剧塑封外壳的失效。

1.2 参数漂移失效模式

参数漂移包括阈值电压漂移、漏电流漂移沟道电阻漂移、跨导下降以及栅击穿等，是功率MOSFET在正常使用过程中最为常见的失效模式。MOSFET的参数漂移是失效机理微观变化下的宏观表现，每种失效模式可能对应多种失效机理，最重要的3种失效机理分别为：热载流子失效HCI、栅氧化层经时击穿TDDB以及负偏压不稳定性NBTI，其中热载流子失效是目前为止研究的最多的一种失效机理［2］。负偏压不稳定性主要发生在P-MOSFET中［23-24］，不再赘述。参数漂移失效模式与失效机理之间的具体关系［33］如表2所示。

1.2.1 MOSFET热载流子的失效机理

在强场作用下，MOSFET中的热载流子呈现出被“加热”的状态，其平均动能远远超过热平衡状态下的载流子，因而被称为热载流子［34］。

表2 功率MOSFET典型参数漂移失效模式及其主要失效机理Tab.2 Typical power MOSFET parameter drift failure modes and their main failure mechanism

载流子通过沟道方向的强电场加速获得能量，在碰撞过程中产生空穴电子对，空穴在较高栅电压和纵向电场作用下进入衬底，形成衬底电流Isub；电子在纵向电场作用下翻过界面势垒进入栅氧化层，其中一部分直接穿越氧化层形成栅电流Ig，另一部分在Si-SiO2交界面产生界面态或被栅氧化层陷阱电荷俘获，严重影响了MOSFET的工作性能［35］，引起阈值电压（Vth）、跨导（Gm）、漏电流等器件电参数退化，从而缩短器件及电路的正常工作寿命。

1.2.2 MOSFET超薄栅氧化层经时击穿的失效机理

栅介质膜击穿现象可分为两大类：高电应力引起的本征击穿和与时间相关的击穿效应。当电场电压过高时，氧化膜产生瞬时击穿；而电压低于临界击穿电场时，氧化层在电场作用下也将产生陷阱，经过一段时间后也会发生退化作用的击穿现象，这一现象会引起功率MOSFET电学参数不稳定，如阈值电压漂移、跨导下降等［37］。

由于MOSFET器件尺寸的缩小，栅氧化层也随之变薄，MOSFET中Si-SiO2势垒高度会随着栅氧化层厚度的减小明显降低［21］。在薄栅氧化层中陷阱的作用下，电子更容易穿过栅氧化层到达栅电极，缺陷周围易形成导电通道从而减少栅氧化层中的聚能。因此，相同电场（低于临界击穿电场）的情况下，超薄栅介质的寿命要比厚栅的长［21］。引入少量杂质或对栅极端介质层厚度进行优化可以使器件寿命大大提高［36］。

1.2.3 负偏压不稳定性的失效机理

负偏压不稳定性NBTI的失效机理通常由反应扩散R-D（reaction-diffusion）理论来解释［24］，其过程分为反应控制阶段、平衡阶段、扩散控制阶段3个阶段［24］。当对p-MOSFET施加NBTI应力时，在界面处将发生应力触发的由空穴、界面和氧化层内与氢相连的缺陷（指Si-H键）参与的可逆电化学反应过程，以及因反应生成的氢物质的扩散过程，此反应和扩散的过程将导致界面陷阱的产生，从而造成器件的负偏压不稳定性退化。

2 MOSFET的寿命模型

目前，MOSFET的寿命预测模型大多数建立在失效机理的基础上。选取失效机理导致的某一种变化量作为敏感参数，以敏感参数的变化值是否达到失效标准值来进行MOSFET的寿命预测，而缺少对不同失效模式下对应寿命预测模型的归纳整理。本文相结合前述MOSFET失效模式，给出了每种失效模式与目前已有的寿命模型/失效判据之间的对应关系，如表3所示。

表3 失效模式与寿命模型/失效判据之间的对应关系Tab.3 Corresponding relationship between failure Modes and life model/fail criterion

对于封装结构失效模式，器件的失效发生为多次功率循环后器件关键部位的瞬间击穿、断裂以及脱落，通常以温度、应力、循环次数达到临界值作为失效判据，以ANSYS仿真及实测验证其失效判据有效可行性的方法；对于参数漂移失效，器件的寿命预测模型一般以参数的退化量达到失效标准值作为判断依据，通常以多组加速老化实验得到寿命预测模型中的关键参数，通过加速老化实验进一步验证其有效可行性。但不同的功率MOSFET封装结构失效模式的寿命预测模型不同，尽管不同的封装模式失效之间会产生一定的影响，但没有全面描述元器件失效的寿命模型。为考虑封装失效模式之间的相互影响，研究者通常在ANSYS仿真对主要的失效模式进行系统建模，而并非对单一失效模式进行单独研究。

2.1 封装失效模式的寿命模型

不同于参数漂移失效，封装结构失效的判定依据不再以退化过程中的敏感参数偏移度达到标准值作为衡量，封装结构失效在于多次循环累计后器件某一部分的突然击穿、断裂或折断。

2.1.1 芯片热击穿失效模式的寿命模型

利用热传导模型一维傅里叶方程来表示材料之间的热传递，即

式中：q为热流密度，W/m2；k为热导率，W/（m·K），不同材料的热导率查手册；A为垂直于热流方向的截面面积，m2；为热流方向上的温度梯度，K/m3。

器件与外表面的空气对流交换，由牛顿冷却定律得到：q=-kAΔT。式中：h为热对流系数，W/（m2·℃）；A为换热面积，m2；ΔT为固体表面和流体的温度差，℃。材料与材料之间、器件与空气之间热传递的过程中遇到的热阻定义为材料两端温度差与通过的耗散功率之比，即。

确定功率MOSFET的几何形状、热导率和热边界条件等。将上述求得的参数带入上述热芯片击穿式（1）中，求出实际结温，通过比较即可判断器件是否发生了热击穿。

2.1.2 黏结层疲劳失效模式的寿命模型

疲劳模型可分为5种：以塑性形变为基础、以蠕变行为为基础、以能量为基础、以应力为基础和以损坏为基础，其中以塑性形变为基础的疲劳模型最为常见［9-11］，其模型为Coffin-Manson方程［12-13］，即

式中：Δε、Δεe和Δεp分别为总应变范围、弹性应变范围和塑性应变范围；Nf为总的循环次数；εf为疲劳延性系数，一般为0.325；E为杨氏模量；σf为疲劳强度系数；b为通过试验确定的材料参数；c为疲劳延性指数，一般为–0.5～–0.7。

Engelmaier［38］修正了Coffin-Manson的疲劳模型，引入频率与温度对循环次数的影响，其修改后的塑性部分关系式为

式中：c为疲劳延性指数，c=-0.442-6×10-4Ts+ 0.017 41n（1+f）,f为循环频率；Δγ为加载循环中总的剪切应变范围；Ts为平均的循环温度。

2.1.3 键合引线断裂失效模式的寿命模型

主要分析键合引线断裂的萌生与发展阶段。复合型裂纹开裂角以及开裂载荷依据基于以下两个前提［39］：①周向正应力最大的方向是初始裂纹扩展方向；②应力强度因子KIC达到临界值，即

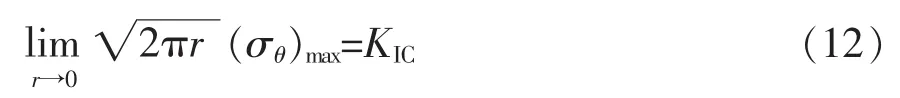
式中：KIC为料断裂韧性，Pa·m1/2；σθ为极坐标系中的周向正应力，Pa；r为裂纹位移，m。在复合型裂纹尖端附近的应力分别为

式中：KI为I型裂纹的应力强度因子，Pa·m1/2；KII为II型裂纹的应力强度因子，Pa·m1/2；σr为极坐标系中的正应力，Pa；τrθ为极坐标系中的剪应力，Pa。

在r=0处，各方向的正应力都趋向正无穷，无法比较其大小，不能确定裂纹扩展方向。文献［15］对距离裂纹尖端奇异点半径为r0（可认为r0无限小）的圆环位置进行研究，计算该位置各节点的应力和角度的极值，即

将式（16）代入到式（15）中可得：KIsin θ+KⅡ·（3cos θ-1）=0。裂纹扩展的临界应力强度因子KI和KⅡ分别确定为

开裂角表示为

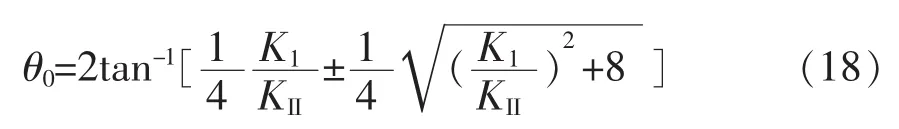
2.1.4 针对塑料封装外壳失效模式的寿命模型

考虑热应力、膨胀应力、蒸汽应力这3种应力对塑料封装外壳的作用。湿气主要由扩散机制进入器件的，遵循 Fick第二定律，对于同种材料，湿气的扩散方程［40］为

由于聚合物材料具有亲水性，不同材料吸收的湿气不同导致产生了不同程度的膨胀变形［31］，温度较高时，材料吸收的湿气将蒸发产生蒸汽压力。文献［41］将这种应力采用热应力的方式进行了等效，得到综合器件在湿热环境下的等效热膨胀系数为

式中：αhygro为湿气引起的膨胀应变等效热应变；αvapor为蒸汽压力引起的等效热膨胀系数变；。再结合湿气扩散系数D、杨氏模量E、饱和湿度Csat、泊松比γ、热膨胀系数CTE、湿膨胀系数CME等基本参数以及稳态温度时的饱和蒸汽压P进行相应的等效热膨胀系数计算。通过热膨胀系数得到器件在湿热环境下的等效热应力，并利用式（6）判断其是否失效。

2.1.5 封装失效模式的寿命预测模型

利用ANSYS对引线框架、焊料层、芯片等进行网格划分成为有限单元，根据传热方式，给定黏结层中的空洞分布以芯片为唯一热源对器件进行建模分析，得到各个部分的温度分布；根据温度分布求取黏结层、键合引线等受到的热应力以及塑料外壳受到的膨胀应力、热应力等，建立整个器件的电-热、热-结构的模型，最终根据失效判据判断器件在实验条件下最先发生的失效模式，从而进行器件的寿命预测。

2.2 热载流子的寿命模型

随着MOSFET尺寸的不断减小，电源电压因电源兼容性的问题不可能完全采用恒场率CE等比例缩小，在横向和纵向电场大大加强的情况下，沟道热载流子注入与高压偏置的问题率显著上升［16］。器件漏极电流Ids、跨导gm、阈值电压Vth是对热载流子效应敏感的主要电参数，受界面态的影响较为明显。因此热载流子寿命定义为这3个参数的退化量ΔIds/Ids0、Δgm/gm0、ΔVth在电应力下达到一定退化量的时间，其中Ids0、gm0为受应力前器件漏电流和跨导。

2.2.1 衬底电流模型

热载流子退化的本质是器件内部高电场产生的碰撞电离，而最易于测量并监测的参数为碰撞电离所产生的衬底电流Isub。为了避免Isub包含不易测量的微观物理量，根据雪崩电离理论，得饱和区的衬底电流模型I-V形式［42-43］为

式中：A和B为电离常数，其中，表面:Ai=2.45×106（cm-1），Bi=1.92×106（cm-1）；体内Ai=0.703×106（cm-1），Bi=1.23×106（cm-1）；Vdsat为漏极电流Ids饱和时的漏源电压；LC为有效导电长度。

2.2.2 阈值电压、漏电流漂移以及跨导下降的寿命模型

1）静态模型

以ΔD表示热载流子退化过程中的敏感参数（ΔIds/Ids0、Δgm/gm0、ΔVth）。选取不同的ΔD，即漏电流漂移ΔIds/Ids0、跨导下降Δgm/gm0、阈值电压漂移ΔVth，则可得参数漂移失效模式下的寿命模型。因与所受电应力时间t呈幂函数关系，则MOFSET热载流子退化模型［47］为

进而得出用于推算器件退化达到一定程度ΔDf所需的时间，即器件的寿命［48］为

式中：H、m、n为与材料、工艺相关的因子。热载流子退化对其值极为敏感，这3个参数的准确提取十分重要［50］。令式（21）中的ηe=1，小尺寸器件中，由于很强的沟道横向电场可能使沟道载流子速度饱和，从而在沟道尚未“夹断”时，漏极电流就已饱和。因此Vdsat不再等于长沟道情况下的Vgs-Vth，而应重新计量，公式为

式中：Ecrit为沟道载流子速度饱和临界电场强度；L为沟道长度。根据经验公式［49］以及最小二乘法推导得到临界电场强度Ecrit、衬底电流模型中有效导电长度LC的值。实验中以较易直接测量的漏电流漂移△Ids/Ids0作为退化表征量，进行参数的求取，即

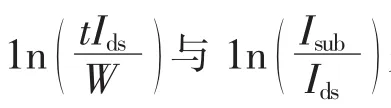
选取阈值电压漂移△Vth、跨导下降△gm/gm作为退化参数，以相同的方法同样可以求取两种失效模式下的寿命模型参数。定义器件寿命为其参数Vth、gm、Ids的退化达到某一失效标准（如△Vth=10 mV，△gm/gm=10%、△Ids/Ids=10%）时所施加的应力时间。将相关标准代入式（10）即可预测出这3种失效模式下的MOSFET寿命。

2）动态应力模型

通常情况下，使用直流或静态应力模型方程式（10）用来描述MOSFET的热载流子特性［51-53］。然而在电路中，MOSFET经受的通常是瞬态栅电压和漏电压应力，则n-MOSFET的交流应力寿命为

式中，T为应力周期。将其中H、m和n看作是与偏压有关的函数［54-55］，则有

式中：Vgd为栅漏电压；Hgd、mgd和ngd分别为H、m和n对栅漏电压的灵敏度。

分别将漏电流漂移△Ids/Ids0、跨导下降△gm/gm0、阈值电压漂移△Vth作为敏感参数△D，利用静态模型中的方法求出参数H、m、n，即可得到针对于漏电流漂移△Ids/Ids0、跨导下降△gm/gm0、阈值电压漂移△Vth的MOSFET动态应力寿命模型。

2.3 栅氧化层的寿命模型

针对栅氧化层的寿命模型基于栅氧化层经时击穿的失效机理之上，目前大都根据器件受电应力后的电场加速情况，从数值上预计超薄栅氧化层的可靠性。它主要分为以下3种模型。

2.3.1 1/E模型

1/E模型又被称为空穴击穿模型（hole induced breakdown model）［56-57］。电子在穿越氧化层时，由于高电场的作用会与晶格碰撞，碰撞散射释放的能量一部分将导致氧化层产生陷阱；另一部分激发了阳极价电子使其进入导带进而生成电子-空穴对，生成的空穴受其迁移率的影响易被陷阱捕获形成的导电通道［58］，从而使氧化层被击穿。这种模型对于高应力电场与实验数据拟合得较好。

1/E模型的表达式为

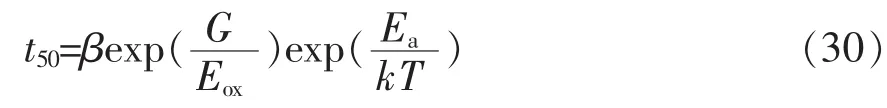
式中：t50为平均击穿时间；β为比例常数；G为比例常数；Eox为加在栅氧化层上的电场强度；Ea为热激活能；k为玻尔兹曼常数；T为绝对温度。由式（30）可以看出，出平均击穿时间的对数与栅氧化层上的外加电场E的倒数成线性关系，这也就是这个空穴击穿模型成为1/E模型的原因。

在一定的电场应力下氧化层TDDB寿命直接与应力电场的倒数有关，则1/E模型也可表示为

式中：tbd为TDDB寿命，s；τ0为本征击穿时间，s；G为模型参数，1×106V/cm;Eox为氧化层电场，1×106V/cm。

对方程取自然对数得

1n tbd对1/Eox关系为一条直线，其斜率及Y轴的截距可求得此时的G和τ0。

2.3.2 E模型

E模型是基于Ering化学反应的热化学击穿，也可以视为线性电场击穿模型，因为击穿时间的对数直接比例于氧化层电场，对较低应力电场与实验数据拟合得比较好［59］。假设氧化层老化和击穿是一个热动力学过程可能由处于热应力和外加电场下的偶极子相互作用破坏了Si-O键而产生击穿。模型表达式为

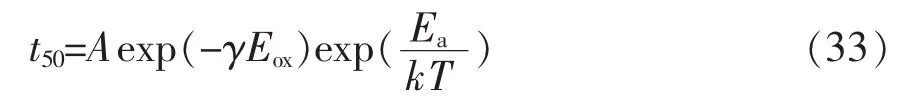
式中：A为比例常数；γ为电场加速参数（field acceleration parameter）。参数求取方法与1/E模型中类似。

2.3.3 1/E与E的统一模型

目前现代的集成电路IC（integrated circuit）电场工作于低电场（＜10 MV/cm）下，为解决上述两种寿命模型在低电场下的不适用性，Hu Chenming提出了一种解决方案，将1/E模型和E模型的优缺点统一，模型中令tbd为统一模型的击穿时间，tbdl和tbd2分别为E模型和1/E模型的击穿时间，则

从模型中可以看出，当电场足够高时，占主导地位的是空穴产生和俘获机制；当电场电压低于隧穿电流的阈值时，以热化学机制作为主要机制。该模型能在膜厚大于5 nm的情况下与实验结果吻合很好，但当氧化层更薄时模型则需要进一步修正。

2.4 基于负偏压不稳定性的寿命模型

由于负偏压不稳定性发生于P-MOSFET中，不做赘述。基于反应扩散R-D过程，关于界面陷阱的产生可描述［24］为

式中：Nit为界面陷阱密度；N0为Si—H键浓度；P为空穴浓度；NH为氢物质（H原子）的浓度；kf为正向反应速率；kr为反向反应速率；DH为氢物质的扩散系数。

根据R-D理论及式（1）～式（3），可得NBTI导致的针对于阈值电压Vth的寿命模型［24］为

式中：A0为常量；Cox为栅氧化层电容，tox为栅氧化层厚度；A和B为对电场相关项的拟合系数，D0为扩散系数；n为幂指数。根据实测数据代入进行最小二乘拟合，最终得到完整的寿命模型。

2.5 经典应力寿命模型

该寿命预测方法不针对于某种特定的失效机理。首先对器件性能退化参数进行数据预处理，确定功率MOSFET在退化过程中的敏感参数为阈值电压Vth、沟道电阻Ron等，考虑参数退化量随应力时间呈幂指数变化、电子元器件正常工作的过程中承受不同的温度应力、电应力等。综合元器件退化效应的主要应力模型为温度应力模型、电应力模型和时间模型。根据这3种应力模型得出综合应力模型对MOSFET进行寿命预测。

2.5.1 经典应力模型

（1）阿伦尼乌斯模型。由大量实验总结出的化学反应速率与温度之间的幂指数关系为

式中：D为电子元器件的某敏感特性参数；V（t）为T温度条件下的退化速率；A为与退化速率无关的常数；E为退化过程的激活能。

（2）艾林模型。逆幂率模型适用于描述器件退化速率与电应力逆幂关系的模型，当温度与电应力分别占主导位置时，与应力有关的函数取不同的函数。而艾林模型同时考虑了温度应力和电应力对电子元器件退化特性的影响，即

式中：ξ为电子元器件性能退化速率；S为电子元器件所受到的环境影响因子；C、a、n为待定系数。

（3）power-law模型。一种由大量数据总结的适用于描述功率电子元器件的敏感参数退化的模型，即

式中：ΔP为敏感参数的变化值；t为加速退化试验进行的时间；n为受到温度和电应力影响的系数。

2.5.2 阈值电压和沟道电阻与温度的函数关系

剩余寿命（remaining useful life）预测是电子元器件可靠性研究的重点。根据文献［60］，阈值电压Vth与温度T的变化率可表示为

式中：NA为沟道掺杂浓度；Eg（T=0）为T=0条件下电场强度；φf为沟道电势；ε0、εr、q及C为常数。式（42）可简化为

文献［61］指出，沟道电阻受载流子迁移率及掺杂浓度的影响，即

式中：T0为室温，300 K；Rds（T0）为室温条件下沟道电阻；α为线性因子。

2.5.3 阈值电压与沟道电阻的综合应力寿命模型

将第2.5.1节中的模型总结得到阈值电压的综合应力模型为

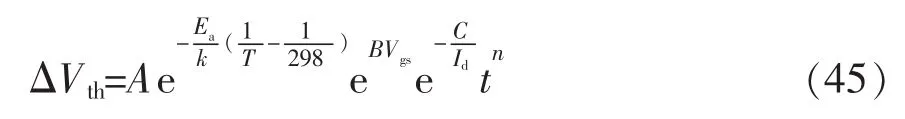
两边取对数得

当实验条件确定时，式中的Vgs、Id、T等为定值。由经验可得，power-law时间系数与器件工作的温度、电应力与常温和最大额定电压Vgsmax电流Idmax比相关，Vgsmax、Idmax可通过查阅手册得到。因此有

根据IEC 62373-2006标准中将变化量为10%设为失效判据。再结合式（45），即可预测出该型号MOSFET的寿命。

同理，沟道电阻的综合应力模型为

求出在沟道电阻达到失效判据的情况下MOSFET的寿命值，比较两者的寿命值，分析哪种敏感参数首先达到失效标准，取较早达到失效标准参数求得的寿命作为MOSFET的预测寿命。

3 寿命模型的应用

在低电压汽车系统、汽车防抱死制动系统ABS（anti-lock braking syste）中通常应用Coffin-Manson公式及其改进寿命公式对系统中的MOSFET进行寿命预测［19，62］，文献［62］以导通电阻20%的漂移作为MOSFET的失效标准，利用Coffin-Manson公式得到热应变测量、温度变化测量、温度变化计算的3个模型，对比分析得到预测汽车系统中MOSFET的寿命预测方法；英飞凌（Infineon）公司在产品大规模推广市场前，在ANSYS中建立其产品的结构模型并利用封装结构失效判据对产品寿命进行预测［63］；文献［64］将DC逆变器的寿命与n-MOSFET的寿命相联系，基于热载流子失效的寿命预测模型与CAS仿真进行了对比分析得出，MOSFET中无8%的电流退化量时会造成1%的传播延迟，为DC逆变器的寿命预测提供了参考依据。

4 结语

本文介绍了由老化造成的MOSFET两种主要失效模式：结构失效与漂移参数失效，同时给出了各种失效模式产生的原因。对已有的MOSFET寿命模型进行了总结，得到各种失效模式与寿命模型/失效判据之间的对应关系以及验证各类模型有效性的实验/仿真方法，并给出不同寿命模型的应用场合。为预测各类工作条件下MOSFET的寿命提供了参考依据。

［1］马晓军,杨宗民,刘春光,等.电力电子器件的实时仿真［J］.电力系统自动化,2013（18）:108-112.Ma Xiaojun,Yang Zongming,Liu Chunguang,et al.Realtime simulation of power electronic devices［J］.Automation of Electric Power Systems,2013（18）:108-112（in Chinese）.

［2］Duong T H，Berning D W，Hefner A R，et al.Long-term stability test system for high-voltage，high-frequency SiC power devices［C］.Proceedings of the 2007 IEEE Applied Power Electronics Conference,Anaheim，CA：IEEE，2007：1240-1246.

［3］Östling M，Koo S M，Lee S K，et al.SiC device technology for high voltage and RF power applications［C］.IEEE International Conference on Microelectronics,Yugoslavia：IEEE，2002 23（1）：31-39.

［4］Wolfgang E.Examples for failures in power electronics systems［OL］.in ECPE Tutorial on Reliability Power Electronic System,Nuremberg,Germany,2007.http://www.ecpe.org.

［5］Fuchs F W.Some diagnosis methods for voltage source inverters in variable speed drives with induction machines-A survey［C］.in Proc.IEEE Industrial Electronics Society Annu.Conf.,2003:1378–1385.

［6］Yang S,Bryant A T,Mawby P A,et al.An industry-based survey of reliability in power electronic converters［J］.IEEE Trans.Ind.Applicat.,2011,48（3）:1441-1451.

［7］Li Xiaojun,Qin Jin,Bernstein J B.Compact modeling of MOSFET wearout mechanisms for circuit-reliability simulation［J］.IEEE Transactions on device and material reliability,2008,8（1）:98-121.

［8］陈世杰.功率MOSFET退化建模及寿命预测方法研究［D］.哈尔滨:哈尔滨工业大学，2013.Chen Shijie.Research of degradation model and lifetime prognosis method for power MOSFET［D］.Harbin:Harbin Institute of Technology,2013（in Chinese）.

［9］Qi Haiyu,Zhang Qian,Tinsley E C,et al.High cycle cyclic torsion fatigue of PBGA Pb-free solder joints［J］.IEEE J Mag,2008,31（2）:309-314.

［10］George E,Das D,Osterman M,et al.Thermal cycling reliability of lead-free solders（SAC305 and Sn3.5Ag）for hightemperature applications［J］.IEEE Trans Device Mater Relat,2011,11（2）:328-338.

［11］刘培生,黄金鑫,陶玉娟,等.PBGA集成电路封装导电胶的疲劳寿命研究［J］.电子元件与材料,2013,32（12）:64-67.Liu Peisheng,Huang Jinxin,Tao Yujuan,et al.Study on the fatigue life of conductive adhesive in PBGA integrated circuit package［J］.Electronic Components and Materials,2013, 32（12）:64-67（in Chinese）.

［12］Niu Ligang,Yang D,Zhao Mingjun.Study on thermo-mechanical reliability of embedded chip during thermal cycle loading［C］.International Conference on Electronic Packaging Technology&High Density Packaging,Beijing:IEEE,2009.

［13］Testa A,Caro S D,Panarello S,et al.Stress analysis and lifetime estimation on power MOSFETs for automotive ABS systems［C］.IEEE Power Electronics Specialists Conference（PESC）.Rhodes,2008:1169-1175.

［14］Kanert W,Pufall R,Wittler O,et al.Modelling of metal degradation in power devices under active cycling conditions［C］.12th Conference on Thermal,Mechanical and Multiphysics Simulation and Experiments in Microelectronics and Microsystems.Linz,2011:1-6.

［15］Fan X J.Moisture related reliability in electronic packaging［R］.Proceedings of Electronic Components and Technology Conference,2007:1-10.

［16］Benda V,Gowar J,Grant D A.Power semiconductor devices:theory and applications［M］.New York:John Wiley& Sons,1999.

［17］Lee P M,Ko P K,Hu C.Relating CMOS inverter lifetime to DC hot-carrier lifetime of NMOSFET's［J］.IEEE Electron device letters,1990,11（1）:39-41.

［18］Kurachi I,Hwang N,Forbes L.Physical model of drain conductance,gd,degradation of NMOSFET’s due to interface state generation by hot carrier injection［J］.IEEE Transactions on electron device,1994,41（6）:964-969.

［19］Russo S,Testa A,Caro S D,et al.Reliability assessment of power MOSFETs working in avalanche mode based on a thermal strain direct measurement approach［J］.IEEE Transactions on industry application,2016,52（2）:1688-1697.

［20］胡恒升.薄氧化硅可靠性及击穿机理研究［D］.上海:中国科学院上海冶金研究所,2000:1-134.Hu Huansheng.Study on thin silicon oxide reliability and Breakdown Mechanism［D］.Shanghai:Shanghai Institute of Microsystem and Information Technology,2000:1-134（in Chinese）.

［21］马晓华，郝跃，陈海峰，等.电压应力下超薄栅氧化层n-MOSFET的击穿特性［J］.物理学报,2006（55）：6198-6121.Ma Xiaohua,Hao Yue,Chen Haifeng,et al.The breakdown characteristics of ultra-thin gate oxide n-MOSFET under voltage stress［J］.Acta Physica Sinica,2006（55）：6198-6121（in Chinese）.

［22］廖翠萍.超薄栅氧化层的TDDB特性与寿命评估［D］.西安:西安电子科技大学,2007.Liao Cuiping.TDDB characteristics and life assessment of ultra-thin gate oxide layer［D］.Xi’an:Xidian University, 2007（in Chinese）.

［23］Zhang Lin,Yi Maoxiang,Yuan Ye,et al.NBTI aging analysis and aging-tolerant design of p-type domino AND gatesp［C］.IEEE International Conference on Electronic Measurement&Instruments,2015:114-118.

［24］张月,卓青青,刘红侠,等.功率MOSFET的负偏置温度不稳定性效应中的平衡现象［J］.物理学报,2013,62（16）:349-355.Zhang Yue,Zhuo Qingqing,Liu Hongxia,et al.Flat-roof of dynamic equilibrium phenomenon in static negative biase temperature instability effect on power metal-oxide-semiconductor field-effect transistor［J］.Acta Physica Sinica,2013, 62（16）:349-355（in Chinese）.

［25］Chen G,Li M F,Ang C H,et al.Dynamic NBTI of p-MOS transistors and its impact on MOSFET scaling［J］.IEEE Electron Device Letters,2002,23（12）:734-736.

［26］陈媛.电子元器件主要失效模式和机理介绍［OL］.Chen Yuan.Introduction of the main failure modes and mechanisms of electronic component［OL］.

［27］Pecht M,Ramappan V.Are components still the major problem:A review of electronic system and device field failure returns［J］.IEEE Transactions on Components,Hybrids,and Manufacturing Technology,1992,15（6）:1-5.

［28］陈颖,孙博,谢劲松,等.高可靠性元器件的使用环境、实验条件和失效机理 ［J］.电子产品可靠性与环境试验, 2007,25（6）:23-30.Chen Ying,Sun Bo,Xie Jingsong,et al.Typical use environmental conditions,test conditions and failur e mechanisms of high reliability electronic components［J］.Electronic Product Reliability And Environmental Testing, 2007,25（6）:23-30（in Chinese）.

［29］Engelmaier W.Fatigue life of leadless chip carrier solder joints during power cycling［J］.Compon Hybrids Manuf Technol,2003,6（3）:232-237.

［30］Hu J,Pecht M,Dasgupta A.A probabilistic Approach for predicting Thermal fatigue life of wirebonding in microelectronics［J］.Journal of Electronic Packaging,1991,113（3）:275-285.

［31］别俊龙,孙学伟,曾松良.吸收湿气对微电子塑料封装影响的研究进展［J］.力学进展,2007,37（1）:35-47.Bie Junlong,Sun Xuewei,Zeng Songliang.Recent advances in the study of moisture absorption in plastic electronic packaging［J］.Advances in Mechanics,2007,37（1）:35-47（in Chinese）.

［33］王蕴辉,于宗光，孙再吉.电子元器件可靠性设计［M］.北京：科学出版社,2007.

［34］郝跃,刘红侠.微纳米MOS器件可靠性与失效机理［M］.北京：科学出版社，2008:42-45.

［35］Hsu C,Tam S.Relationship between MOSFET degradation and hot—electron induced interface—state generation［J］.IEEE Electron Device Lett,1984,5（2）:50-52.

［36］胡恒升.薄氧化硅可靠性及击穿机理研究［D］.上海:中国科学院上海冶金研究所,2000:1-134.Hu Huansheng.Study on thin silicon oxide reliability and Breakdown Mechanism［D］.Shanghai:Shanghai Institute of Microsystem and Information Technology,2000:1-134（in Chinese）.

［37］Kunhyuk K,Sang P,Kaushik R,et al.Estimation of Statistical variation in temporal nbti degradation and its impact on lifetime circuit performance［C］.IEEE International Conference on Computer Aided Design,2007:730-734.

［38］Engelmaier W.Fatigue life of leadless chip carrier solderjoints during power cycling［J］.Compon Hybrids Manuf Technol,2003,6（3）:232-237.

［39］Fan X J.Moisture related reliability in electronic packaging［R］.Proceedings of Electronic Components and Technology Conference,2007:1-10.

［40］刘玉岭,檀柏梅,张楷亮.微电子工程-材料、工艺与测试［M］.北京:电子工业出版社,2004:149-185.

［41］李求洋.功率MOSFET可靠性建模的研究［D］.哈尔滨:哈尔滨工业大学,2012.Li Qiuyang.Research on power MOSFET model for reliability analysis［D］.Harbin:Harbin Institute of Technology, 2012（in Chinese）.

［42］Mar J,Li S S,Yu S Y.Substrate current modeling for circuit simulation［J］.IEEE Trans.CAD,2006,1（4）:183-186.

［43］Chen T Y,Ko P K,Ho C.A simple method to characterize substrate current in MOSFET’s［J］.IEEE Electron Devices Lett,1985,5（12）:505-507.

［44］Sze S M.Physics of semiconductor devices［M］.NewYork :Wiley,1981.

［45］Heremans P,Den Boshch G V,Bellens R,et al.Temperature dependence of the channel hot-carrier degradation of nchannel MOSFET’s［J］.IEEE Trans Electron Devices,1990, 37（4）:980-993.

［46］陈勇.MOSFET热载流子退化效应的研究［D］.成都:电子科技大学,2001:25-28.Chen Yong.Study of hot carrier degradation effects of MOSFET［D］.Chengdu:University of Electronic Science and Technology,2001:25-28（in Chinese）.

［47］Hu C,Tam S C,Hsu F C,et al.Hot-electron-induced MOSFET degradation-model,monitor,and improvement［J］.IEEE Trans.Electron Devices,1985,20（1）:295-305.

［48］Weber W,Werner C,Schwerin A.Lifetime and substrate currents in static and dynamic hot carrier degradation［J］.IEDM Tech.Dig.,1986:390-393.

［49］Chen Wenliang,Balasinski A,Ma T P et al.Lateral distribution of radiation-induced damage in MOSFET’s［J］.IEEE Trans.Nuclear science,1992,38（6）:1124-1129.

［50］杨漠华,于奇,王向展,等.MOSFET热载流子退化/寿命模型参数提取［J］.半导体学报,2000,21（3）:268-273.Yang Mohua,Yu Qi,Wang Xiangzhan,et al.Model parameter extraction for MOSFETs hot carrier degradation/age［J］.Chinese Journal of Semiconductors,2000,21（3）:268-273（in Chinese）.

［51］Borx M,Weber W.Dynamic degradation in MOSEFT’s（part l）the physical effects［J］.IEEE Trans.Electron Devices,1991,38（8）:1852-1858.

［52］Doyle B,Bourcene M,Marchetaux J C,et al.Interface state creation and charge trapping in the medium-to-high gate voltage range（Vd/2≥Vg≥Vd）during hot-carrier stressing of n-MOS transistor［J］.IEEE Trans.Electron Devices,1990, 37（3）:744-754.

［53］Tsuchiya T,Okazaki Y,Miyaka M,et al.New hot-carrier degradation mode in lifetime prediction method in quartermicrometer PMOSFET［J］.IEEE Trans.Electron Devices, 1992,39（2）:404-408.

［54］Kuo M M,Seki K,Lee P M,et al.Simulation of MOSFET lifetime under AC hot-electron stress［J］.IEEE Trans.Electron Devices,1988,35（7）:1004-1011.

［55］Quader K N,Ko P K,Hu C,et al.Simulation of CMOS circuit degradation due to hot-carrier effects［C］.IEEE IRPS-92 Tech.Dig.,1992:16.

［56］Takayanagi M，Takagi S,Toyoshima Y.Gate voltage dependent model for TDDB lifetime prediction under direct tunneling regime［C］.Symposium on VLSI Technology Digest of Technical Papers,2001:99-100.

［57］Zhang Weidong,Zhang J F,Lalor M,et al.Two types of neutral electron traps generated in the gate silicon dioxide［J］.IEEE Transactions on Electron Devices,2002:49（11）:1868-1875.

［58］Duschl R,Vollertsen RP.Voltage acceleration of oxide breakdown in the sub-10 nm fowler-nordheim and direct tunneling［C］.2005 IRW Final Report,2005:44-48.

［59］McPherson J W,Baglee D A.Acceleration factor for thin gate oxide stressing［J］.IEEE International Reliability Physics Symposium,1985:1-4.

［60］孟庆巨,刘海波,孟庆辉.半导体器件物理［M］.北京：科学出版社,2005.

［61］陈星弼.功率 MOSFET与高压集成电路［M］.南京：东南大学出版社,1990:31-33.

［62］Testa A,Caro S D,Panarello S,et al.Stress analysis and lifetime estimation on power MOSFETs for automotive ABS systems［C］.IEEE Power Electronics Specialists Conference（PESC）.Rhodes,2008:1169–1175.

［63］Kanert W,Pufall R,Wittler O,et al.Modelling of metal degradation in power devices under active cycling conditions［C］.12th Conference on Thermal,Mechanical and Multiphysics Simulation and Experiments in Microelectronics and Microsystems.Linz,2011:1-6.

［64］Lee P M,Ko P K,Hu Chenming.Relating CMOS inverter lifetime to DC hot-carrier lifetime of NMOSFET’s［C］.IEEE Electron Device Letters,1990,11（1）:39-41.

Review of MOSFET Lifetime Model

ZHA Xiaoming,LIU Yuexia,HUANG Meng,LIU Yi
（School of Electrical Engineering,Wuhan University,Wuhan 430072,China）

MOSFET is the cardinal device to achieve the basic function of power electronic converters,but its short lifetime is a major restriction to the reliability of power electronics system.Aging failures of MOSFET can be classified by package failure and parameter drift failure,the former is generated by the deterioration of defects resulted from the manufacturing and material under certain working conditions;the latter is its parameter drift derived from internal microscopic degradation in the usage.This paper summarizes the relevant research results of MOSFET lifetime model, classifies MOSFET failure modes,and establishes the corresponding MOSFET lifetime model of different failure modes, and further summarizes the failure criteria and experimental verification methods of each lifetime model.

MOSFET;lifetime model;package failure;parameter drift failure

查晓明

俞珊

查晓明（1967-），男，博士，教授，博士生导师，研究方向：电力电子与电力传动、电力系统及其自动化，E-mail xmzha@ whu.edu.cn。

刘悦遐（1993-），女，通信作者，硕士研究生，研究方向：电力电子器件可靠性，E-mail:whliuyx@whu.edu.cn。

黄萌（1984-），男，博士，副教授，研究方向：电力电子变换器、非线性分析、新能源微网，E-mail:meng.huang@whu.edu.cn。

刘懿（1988-），男，博士研究生，研究方向：电力电子可靠性，E-mail:aaronlau@ whu.edu.cn。

10.13234/j.issn.2095-2805.2016.6.108

TM 407

A

2016-08-13

国家自然科学基金重点资助项目（51637007）；国家自然科学基金资助青年项目（51507118）

Project supported by the State Key Program of National Natural Science of China（51637007）;National Natural Science Foundation of China for Distinguished Young Scholars（51507118）