四参数坐标转换中的稳健估计与精度分析
2016-12-19李卫强汪金花李广张云英
李卫强,汪金花,李广,张云英
(华北理工大学 矿业工程学院,河北 唐山 063009)
四参数坐标转换中的稳健估计与精度分析
李卫强,汪金花,李广,张云英
(华北理工大学 矿业工程学院,河北 唐山 063009)
四参数坐标转换;最小二乘原理;粗差;稳健估计
在进行GNSS坐标系统之间相互转换的坐标拟合时,一般会采用最小二乘原理(LS)法对坐标转换参数进行求解,这就要求已知的坐标数据中不存在粗差,一旦粗差引入求解模型,就会导致转换结果失真,大大影响坐标转换精度。利用稳健估计的方法可以消除或者减弱在参数求解过程中粗差的影响,以提高坐标转换精度。文中以唐山市滦县某地区西安80和北京54三等控制点坐标数据转换为例,利用四参数转换原理与稳健估计相结合,通过粗差测试和转换后精度分析,验证了稳健估计方法能有效提高模型的抗差性,提高转换精度。
工程测量中常会遇到多种坐标系统并行的情况,坐标系统之间的相互转换是应用GNSS定位技术不可避免的问题。当GNSS测量定位的地区已建有国家控制网或地方控制网的地区时,往往要求将GNSS测定的点位成果纳入到国家坐标系统(北京54坐标系统或西安80坐标系统)或者地方坐标系统中,这就需要将GNSS的坐标系统转换。坐标系统转换的实质是求解坐标系统转换参数,常见的坐标转换方法主要有七参数转换、四参数转换方法。当测区面积较小时或工程区域不大情况下,已知点要求相对比较低,采用四参数坐标转换能够达到理想精度。
在参数解算过程中,为了得到转换参数的最佳值,通常釆用最小二乘估计(LS)。随着测量数据的自动化和现代化,测量数据中粗差不可避免的存在于数据中,并且造成观测值有偏于正态分布假设,LS估计不具有抗差性,观测值中的粗差可能导致参数解面目全非,稳健估计方法能有效地消除或减弱粗差对于坐标系统转换参数的影响。文中采用稳健估计对四参数转换模型参数求解进行了试验,采用不同大小粗差对比分析,验证了稳健估计在坐标转换抗差效果和影响精度。
1 稳健估计下四参数坐标转换
平面坐标转换模型只考虑四个转换参数。四参数是一种降维的计算方法,即把三维空间的坐标转换成二维的平面坐标,根据坐标的相对位置关系进行计算。
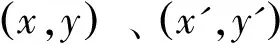
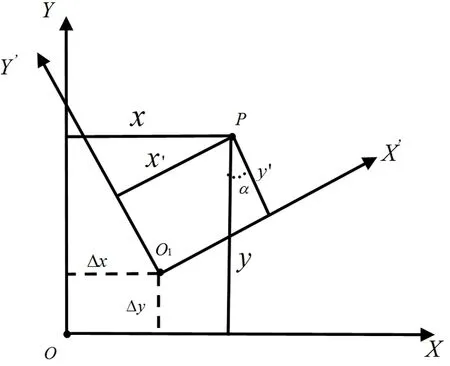
图1 2个坐标系下的参数
(1)
令:M=mcosα、θ=msinα,按照间接平差模型可以得到公式(2):
(2)
其中ΔX、ΔY、M、θ即为四参数,将上式按照V=Bδx-l提取系数矩阵,如公式(3)所示:
(3)
将上述转换模型按照稳健估计方法解算:
(4)
式中Pi是稳健估计的初始权阵,按照一般定权方法确定。当控制点坐标默认同精度观测条件时,可以假设初始权为单位权阵,wi是稳健权因子,k通常是个常数,可以假设为趋近零的数,如10-10。主要是避免稳健权因子wi计算时出现溢出。
2 工程应用与试验分析
为了验证稳健估计对含有粗差的观测数据有明显抗差性,从而提高转换结果的精度。试验选取了唐山市滦县某地区坐标为研究数据,分层逐级检验稳健估计在坐标转换过程中有效性。
2.1 数据来源
研究区位于唐山市滦县东部,北部是山区,南部是相对平坦的居民地,整个测区范围内地势北高南低。整个区域面积约为500 km2,其中南北最大跨度约42 km,东西跨度最大约为18 km。
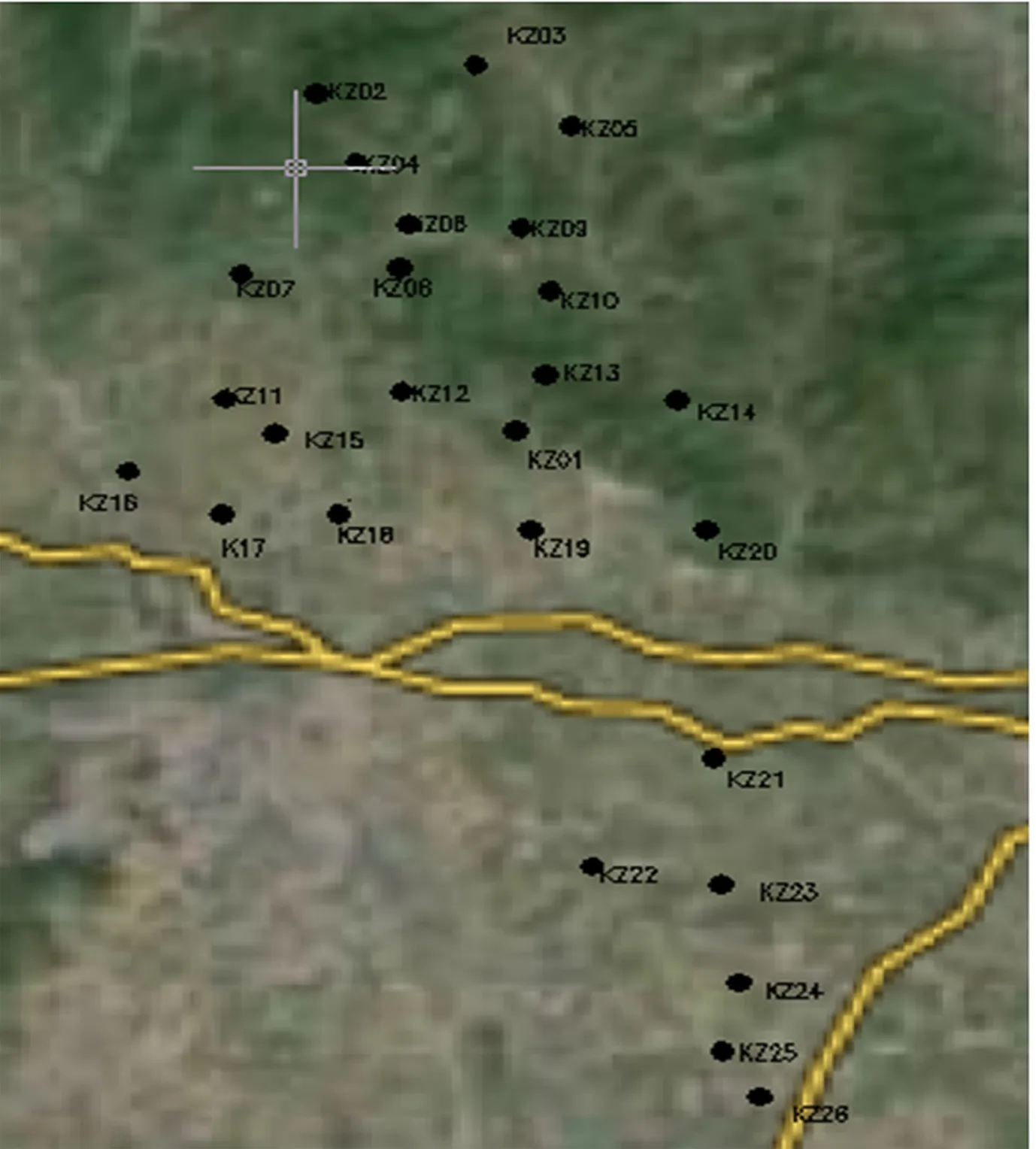
图2 控制点分布示意图
测区内共布置了26个控制点(如图2),分布较均匀。野外实测了控制点的西安80的北京54同期观测的控制点坐标,控制网联测的点位中误差数量级为毫米级,满足三等控制点精度要求。选取其中的KZ5、KZ13、KZ19、KZ24 4个点作为转换模型的假设检验。(由于数据保密原因,部分数据进行了处理,如表1所示。)
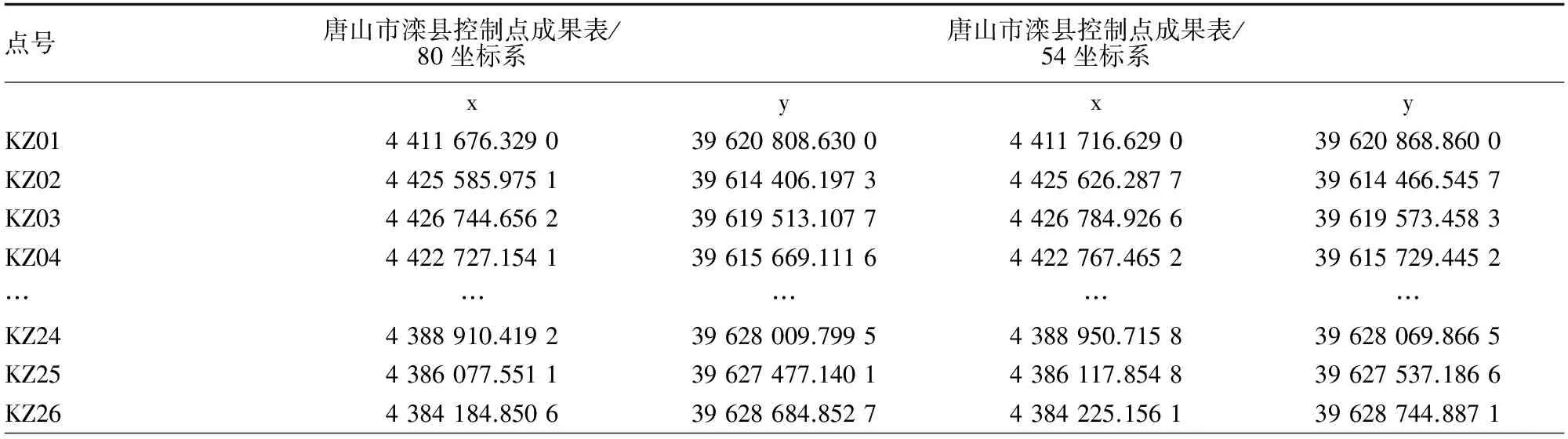
表1 部分控制点坐标表
2.2 四参数的解算
分别利用LS法和稳健估计法对试验区域控制点坐标进行西安80向北京54坐标系统的参数求解和坐标转换。为了验证稳健估计的抗差性,选取均匀分布的KZ3、KZ15、KZ20、KZ26中加入了固定误差△,分别为三等控制点精度要求α=10 mm的1倍、2倍、3倍,分别利用LS法和稳健估计法对参数进行求解,并根据转换坐标与原坐标之差求得内符合精度,所得结果如表2、表3所示。

表2 最小二乘原理法转换参数与精度表

表3 稳健估计法转换参数与精度表
根据表2、表3中2种方法求得的四参数数据可以看出,利用LS法进行求解的转换参数随着误差的增加,参数的变化不断增大,而相对于稳健估计方法随着误差的增加,参数趋于一个相对稳定的结果。由表中内符合精度结果可以看出:利用LS在粗差为0时精度为4.14 mm,随着加入粗差的不断增大,坐标转换的精度也随着大幅降低,当误差增加到△=3α时,误差增加为7.66 mm,解算精度大大降低;而利用稳健估计的方法在粗差为0时精度为4.28 mm,略高于LS法,当误差增加到△=3α时,误差为4.35 mm非常接近于无粗差转换精度。
根据上述结果可以得出:当观测值中不包含粗差时,稳健估计的方法会造成一定的精度损失,但是这种损失会非常的小,对坐标转换的精度影响不明显;当观测值中存在着粗差时,LS的抗差性比较弱,在坐标转换过程中受到粗差影响较大,利用稳健估计的方法可以发现粗差并对粗差进行减弱和剔除,从而大大提高了转换精度,因此稳健估计法的抗差性远远优于LS法。
2.3 转换结果验证
根据表2、表3数据,利用加入粗差△=3α所求得到的参数,利用公式(2)对假设的4个未知点数据进行坐标转换,所得结果与已知坐标数据对比所求得的残差如表4所示:
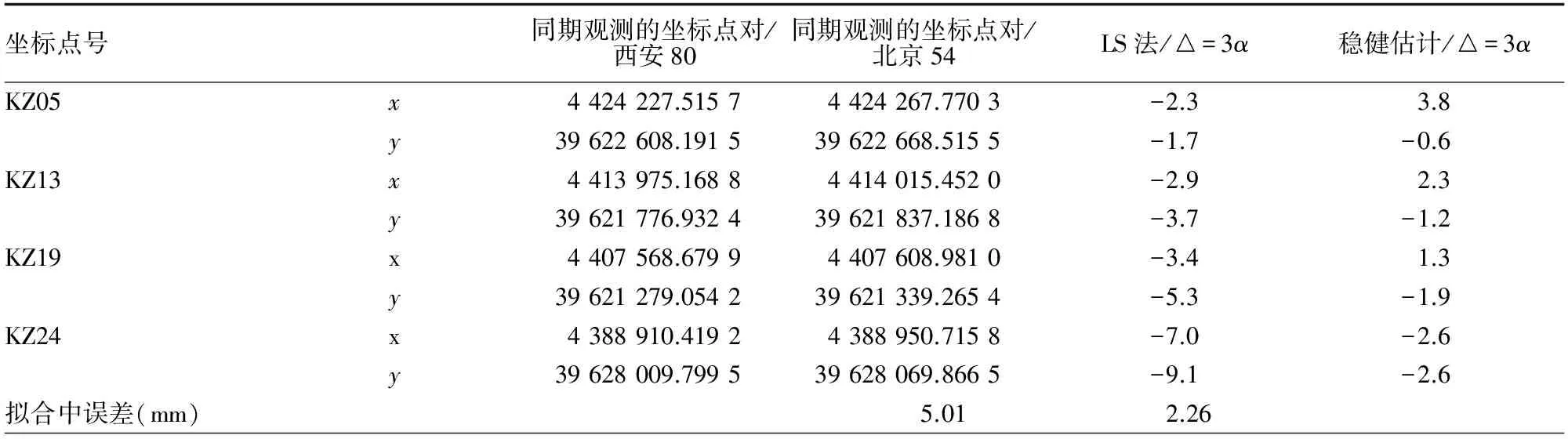
表4 转换后坐标残差对比
由表4可以看到,已知数据中存在着粗差(△=3α),在利用LS进行坐标转换时所求解的转换坐标与假设未知点的已知坐标在y方向最大相差9.1 mm,在x方向最大相差7 mm;而利用稳健估计的方法所求得的转换坐标与原坐标相差最大为2.6 mm,转换精度为2.26 mm相较于LS法精度5.01 mm大大提高了。因此利用稳健估计在进行已知数据含有粗差的坐标转换中有明显的优势。
3 结论
随着数据采集的现代化,大量的测绘数据如何进行处理成为了研究的热点。论文结合传统的四参数模型理论,通过加入粗差的仿真实验,利用LS法与稳健估计对转换数据进行对比,证明了稳健估计的方法的抗差性远远优于LS法;目前数据采集中往往存在着无法辨别的粗差,因此利用稳健估计在坐标转换方面有一定的应用前景和优越性。
[1]汪金花,刘雨青,吴长悦.一种含稳健权的神经网络GNSS高程拟合模型[J].测绘通报.2014,(08):14-16.
[2]冯骥.四参数坐标转换原理和程序设计[J].科技资讯.2013,16(06):35-37.
[3]刘达,韩晓冰,房龙.三维直角坐标系直接转换算法的研究与实现[J].测绘与空间地理信息.2012,35(05):175-178.
[4]牛丽娟.测量坐标转换模型研究与转换系统实现[D].西安:长安大学,2010.
[5]朱元彪,陈华.工程常用坐标转换方法研究与分析[J].测绘信息与工程.2012,37(02):35-37.
[6]于彩霞,黄文骞,樊沛.Bursa的3参数模型与7参数模型的适用性研究[J].测绘科学.2008,33(02):96-97.
Robust Estimation and Precision Analysis on Four-parameter Coordinate Transformation
LI Wei-qiang, WANG Jin-hua, LI Guang, ZHANG Yun-ying
(College of Mining Engineering, North China University of Science and Technology, Tangshan Hebei 063009, China)
four-parameter coordinate transformation; principle of least square; gross error; robust estimation
When making coordinate fitting for the interconversion among GNSS coordinate system, least squares (LS) method is usually adopted to calculate the coordinate transformation parameters, which requires no gross error existing among the known coordinate data. Once the gross error is introduced to the calculation model, distortion will appear and the precision of coordinate transformation will be greatly affected. By robust estimation, the influence of gross error can be eliminated or weakened in the process of parameters calculation, thus the precision of coordinate transformation can be improved. Taking third grade control point coordinate data transformation of Xi'an 80 and Beijing 54 in Luanxian county of Tangshan as an example, this paper combines four-parameter coordinate transformation with robust estimation, and verifies the fact that model robustness and transformation accuracy can be effectively improved by robust estimation after gross error test and transformation accuracy analysis.
2095-2716(2016)01-0024-05
2015-09-05
2015-12-07
国土环境与灾害监测国家重点实验室基金项目:(LEDM2013B06),河北省教育厅重点科技项目(ZD20131040),唐山市科技支撑项目(13130218Z),河北省矿业开发与安全技术实验室的资助。
P207+.1
A
