基于FCM算法的煤矿瓦斯涌出量分析

吕赛，何玉秋，刘晓悦

(华北理工大学 电气工程学院，河北 唐山 063009)



基于FCM算法的煤矿瓦斯涌出量分析

吕赛，何玉秋，刘晓悦

(华北理工大学 电气工程学院，河北 唐山 063009)

瓦斯涌出量；最大最小距离算法；FCM算法

对于矿井瓦斯涌出量受多参数制约，常规线性系统已经不再适用。对于多个传感器大数据采集处理系统，简单的线性数学模型已经不能满足要求，因此本文提出基于FCM算法对煤矿瓦斯涌出量进行分析。首先采用最大最小距离算法确定FCM算法的初始聚类中心，然后采用FCM算法对数据进行处理和分析，从而得到更加精确瓦斯涌出量。

0 引言

中国是一个产煤大国，而在开采煤的过程中，矿井下的环境安全问题就成了人们关注的焦点。其中，瓦斯事故是造成人员伤亡和财产损失最严重的因素。长期以来，人们都是以单一的瓦斯传感器监测瓦斯含量为主要依据，数据量单一，在很大程度上依赖仪器的精确度。由于矿井下环境复杂，瓦斯涌出量受多种因素的制约，所以必须综合考虑多方面因素对瓦斯涌出量的影响程度。设计多个传感器采集矿井下的环境数据，将采集到的数据进行数据分析，提取有关参数的状态特征，更加准确捕获瓦斯发生前的前兆特征信息。因此瓦斯灾害准确预测的研究是制定相应的防护措施、减少矿难发生的极为重要关键工作。

煤矿下的瓦斯来源有很多，分为回采区、掘进区和已采区。对一个生产矿井来说，了解矿井的瓦斯来源，对正确制定相应的防护措施、减少矿难的发生十分重要。

瓦斯涌出量的大小主要取决于下列因素：

地质构造、瓦斯压力、煤的坚固性系数、煤层开采深度、瓦斯放散初速度、钻屑瓦斯解吸指标、地面大气压力变化、煤层倾角、开采顺序、开采方法、煤层和围岩的瓦斯含量、煤层开采规模等。

由此可见，多个传感器得到的数据是大数据，简单的线性数学模型已经不能完整分析和描述大数据。本文基于FCM聚类算法对数据进行处理和分析，从而对瓦斯涌出量进行更加精确的分析，为确定BP神经网络的初始条件，构造神经网络模型的结构奠定基础。

1 最大最小距离算法

FCM算法对初始聚类中心的选择特别敏感，若初始聚类中心选择不当，FCM算法很容易陷入局部最小点，而得不到全局最优解。因此，本文采用最大最小距离算法来确定FCM算法的初始聚类中心，将其得到的聚类中心数作为FCM算法的初始化条件，克服了FCM算法初始化时人为确定初始化聚类中心而引起的误差，使结果更加精确。

该项研究基于欧式距离度量来计算对象间的相异度。最大最小距离算法的具体流程如下：

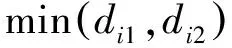
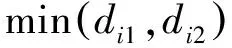
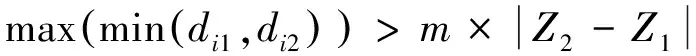
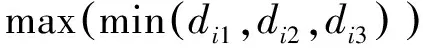
如果满足上述不等式，将新的对象作为新的聚类中心，用同样的方法继续计算新的对象，直到再找不到符合条件的新的聚类中心，此时算法结束。

2 FCM算法

FCM算法是在普通C均值算法的基础上改进的一种算法，普通C均值算法是一种硬性的数据划分，而FCM算法则是一种柔性的模糊划分。

FCM算法严重依赖于聚类数目c的选择，聚类数目已经通过最大最小距离算法得到，然后使用FCM算法。

FCM的算法步骤如下：

(1)用最大最小距离算法所得到的初始聚类中心对FCM算法进行初始化，令初始化聚类中心为ci。定义1个c×n的二维隶属矩阵U。若第j个数据点xj属于组i，则U中的元素uij=1；否则，该元素取0。

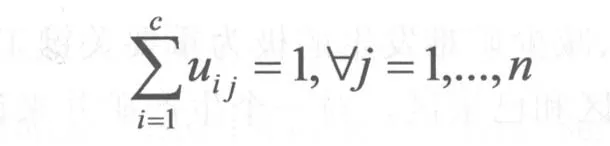
(1)

计算uij及价值函数，可以构造出如下的目标函数。

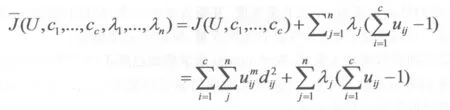
(2)

式中：λj,j=1,…,n为约束式的拉格朗日乘子；

dij=‖ci-xj‖为第i个聚类中心与第j个数据点间的欧几里德距离；

(3)

进而可以得出uij，若计算结果或它相对上次目标函数值的改变量小于某个阈值，则算法停止，并由下式计算矩阵U。

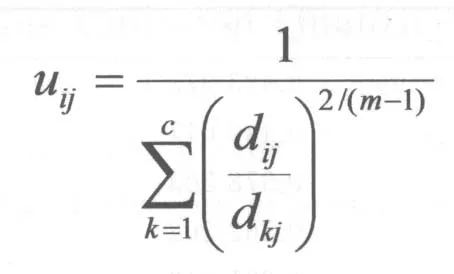
(3)用计算出的新得矩阵U返回求ci，直至满足阈值要求。

3 仿真结果

选取某煤矿瓦斯涌出量的部分影响因素作为结合算法的输入量。部分影响因素包括开采深度、瓦斯压力、巷道类型、煤层倾角、放散速度、坚固系数、地质构造、开采方式8个主要参数。其中，巷道类型0代表斜巷，1代表平巷。地质构造中0代表褶皱，1代表断层。开采方式中0代表炮采，1代表综采。部分数据如表1所示。

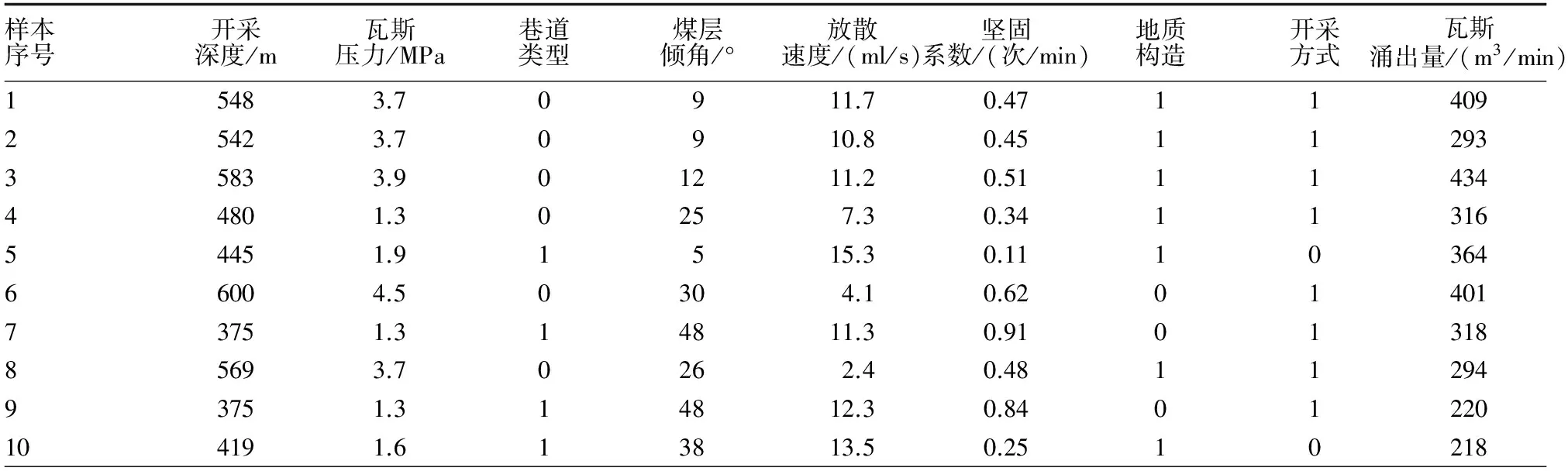
表1 部分样本数据

从表1中可以看出，各个样本的不同属性的数据值相差较大，如果直接运用这些数据对以后的运算影响太大。为了避免数据溢出，对所有的样本数据进行归一化处理，表1中的部分数据处理后的结果如表2所示。

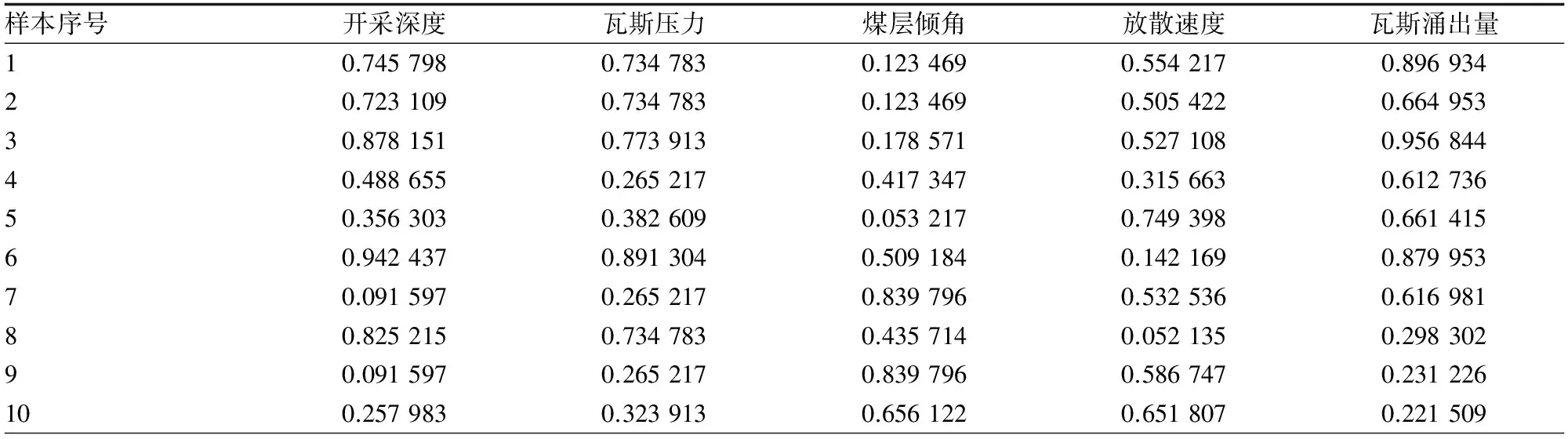
表2 部分数据的归一化

首先将归一化后的数据用最大最小距离算法算出初始聚类中心。如前所述，计算迭代欧式距离dij，聚类中心Zi(计算过程略)，计算结果为初始聚类中心有4类，由表1可以看出样本数据是一个8维数据，所以得到的类别中心的每一个中心点也是一个8维数据，结果如表3所示。

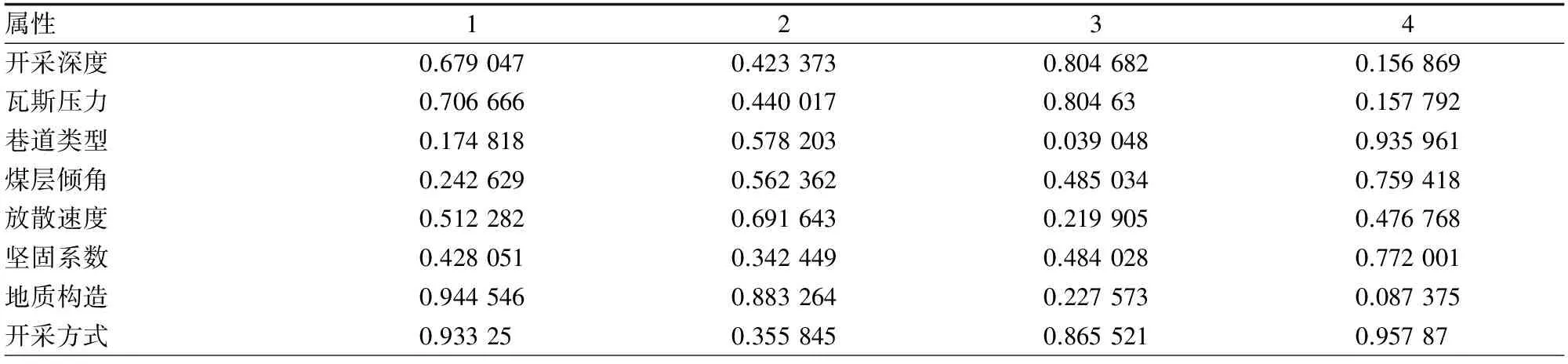
表3 聚类中心

然后将得到的初始化聚类中心作为FCM算法的初始化条件，经过FCM算法计算，每个数据均可以用隶属度值来表示其类别，从而得到隶属度矩阵U。

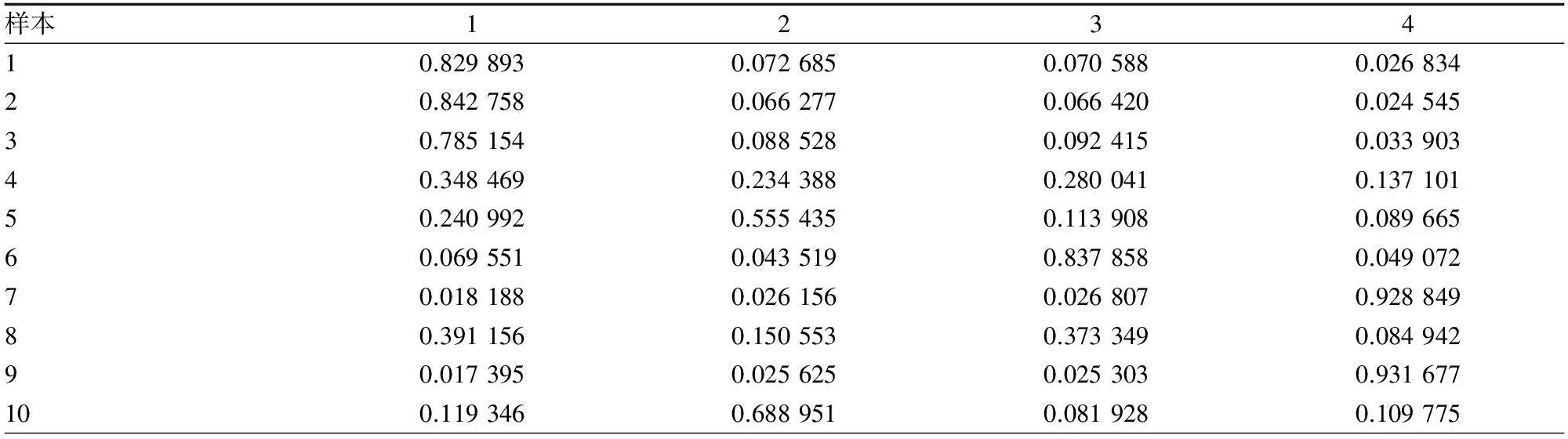
表4 隶属度矩阵U

表4中列出了表1中的数据相对于4个聚类中心的隶属度。根据隶属度矩阵，按照模糊集合中的最大隶属度原则就能够确定出每个样本数据大概属于哪个类型。

经过FCM算法聚类后，将处理过的数据和处理过程中得到的数据结果结合起来，可以得到各个因素对瓦斯涌出量的影响程度。

4 结论

(1)由于煤炭开采的环境条件复杂，使煤矿瓦斯涌出量受很多方面因素的影响，且影响程度不同。本数据分析方法充分考虑了数据的影响因子、权重及数据的边缘性，聚类分析结果数据融和度较高。

(2)通过结果的分析显示，采用最大最小距离算法得到FCM算法的初始聚类中心，然后用FCM算法对影响瓦斯涌出量的影响因素的样本数据进行模糊聚类分析，得到了各个因素对瓦斯涌出量的影响程度，为后期实现更加精确的瓦斯涌出量预测分析奠定基础。

[1]罗俊玮. 基于FCM的类合并聚类算法研究[D]. 重庆:重庆大学,2009.

[2]刘亿文. 基于模糊神经网络的煤矿瓦斯涌出量预测研究[D]. 唐山:河北联合大学,2012.

[3]刘晓悦,封素敏. 基于模糊神经元网络的信息融合模型[J]. 河北理工大学学报(自然科学版)2008,30(03):70-73.

[4]刘晓悦,胡珍,徐如敬. 基于模糊综合评判的控制系统性能评估[J]. 河北联合大学学报(自然科学版)2013，35(01)：46-50.

[5]于迪. 模糊聚类分析在煤与瓦斯突出事故预测中的应用研究[D]. 阜新:辽宁工程技术大学,2012.

[6]曾山. 模糊聚类算法研究[D]. 武汉:华中科技大学,2012.

Analysis of Coal Mine Gas Emission Quantity Based on FCM Algorithm

LV Sai, HE Yu-qiu, LIU Xiao-yue

(College of Electrical Engineering, North China University of Science andTechnology, Tangshan Hebei 063009, China)

quantity of gas emission; max-min distance algorithm; FCM algorithm

Because the mine gas emission quantity is influenced by many parameters, conventional linear systems are no longer applicable. Faced with the big data, simple linear mathematical model has been unable to meet the requirements. The way to analyze gas emission quantity based on FCM algorithm was put forward in the paper. The initial clustering center of FCM algorithm is determined by the max-min distance algorithm in this paper. Then the data is processed and analyzed by using FCM algorithm so as to get more accurate gas emission quantity.

2095-2716(2016)01-0001-05

2015-10-26

2015-12-10

TD712+.53

A