双重不确定环境下指派模型的研究及应用

肖继先，寇春蕾

(华北理工大学 理学院，河北 唐山 063009)



双重不确定环境下指派模型的研究及应用

肖继先，寇春蕾

(华北理工大学 理学院，河北 唐山 063009)

随机模糊变量；指派问题；期望值；等价变换

在指派问题中加入了对资源量限制的考虑，给出一种含有双重不确定变量的多目标指派问题模型。设计了一种等价转换方法对该模型进行求解，即将随机模糊变量的密度函数转化成为具有概率密度性质的函数，以此计算随机模糊变量的期望值，并采用数值算例对方法进行了验证。说明该方法的合理性和可行性。

引言

指派问题(Assignment Problem)是运筹学里的一类经典问题，属于0-1规划的特例。此类问题最早出现在Votaw和Orden的文献中，真正得到发展是在1955年Kuhn给出求解这类问题的匈牙利算法以后。在实际的生产管理中，指派问题有着广泛的应用，如在生产服务系统、资源优化、项目选择、军事作战等领域中都有重要应用[1,2]。

传统的指派问题是指在效益矩阵(或费用矩阵、时间矩阵)精确已知的条件下，确定m个人完成m项任务的最优指派方案，这类问题可以用匈牙利法、隐枚举、分支定界法等很好地解决[3,4]。但是在实际问题中，由于各人的专长与能力不同，完成各项任务的效益(或费用、时间等)也就各不相同。更多的时候效益矩阵(或费用矩阵、时间矩阵等)不能精确得到，因此在做决策时经常会遇到不确定的效益矩阵(或费用矩阵、时间矩阵等)。这样就有必要在做决策时对矩阵中的数据进行统计或粗略统计，从而产生了不确定环境中的指派问题[5,6]。这种不确定性不再是单一的呈现出随机性和模糊性，而是相互渗透的结果——随机模糊性和模糊随机性。

基于上述原因，提出了一种双重不确定环境中的指派问题，并给出了一种等价变换计算方法，该算法不但简便，而且有良好的运算效率和近似效果。

1 数学模型

1.1 问题描述

传统的指派问题中只有一个目标函数，但一般情况下指派在追求一定利润的同时，还可能考虑工作成本、工作时间等。因此在实际问题中，目标往往不止一个，这样就形成了含有多个目标的指派问题。另外，传统的指派问题不考虑资源约束，但实际中，每个人拥有的资源量是有限的，所以在该研究中加入了资源限制。多目标指派问题的具体描述如下：

设将n项任务分配给m个人，指派方案满足如下要求：

(1)每个人可以独立地完成任何一项任务。

(2)每项任务只能由一个人来完成，且所有的任务都必须完成。

为表示方便，将建模过程中用到的若干符号列在下表。

表1 符号列表

1.2 随机模糊指派问题的期望值模型

在建模过程中，由于很多因素是不确定的，因此常常考虑目标函数的期望值，追求能够使期望值达到最优的可行解x。其期望值模型如下：

(1)

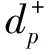
2 模型求解

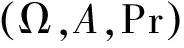
(2)

为随机变量ξ的期望值[7]。

定义2设ξ为模糊变量，则称

(3)

为模糊变量ξ的期望值。

(4)

为随机模糊变量ξ的期望值[7]。

引理1设φ是随机变量ξ的概率密度函数，若Lebesgue积分

存在且有限，则

(5)

引理2设φ是模糊变量ξ的隶属函数，若Lebesgue积分

存在且有限，则

(6)

引理3设φ是随机模糊变量ξ的密度函数，若Lebesgue积分

存在且有限，则

(7)

证明 根据期望值的定义和Fubini定理，有

证毕[8]。

(8)

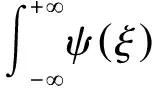
通过定理1引入等价概率密度函数，可以将随机模糊变量期望值的计算等价转换成随机期望值的计算，并且等价概率密度函数的分布参数与随机模糊变量的密度函数和隶属函数参数之间存在解析关系。

把定理1的式(8) 代入引理3的式(7)中，即可得到期望值的另一种表达方式如下：

(9)

3 算例

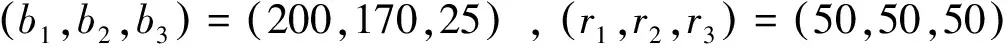
模型有关数据如下：

表2 指派问题的利润矩阵

表3 指派问题的费用矩阵

表4 指派问题的时间矩阵

表5 指派问题的资源消耗量矩阵

建立上面问题的数学模型，并利用定理1及定理2变换为等价形式：

(10)

转换为等价模型为：

(11)

求解，可得最优解为：

即x12=x14=x21=x33=x35=1。

代入模型，验证可得：

满足要求，所求解为较优指派方案。

4 结论

(1)给出了双重不确定环境中的指派问题，并在该问题中加入了资源量限制的考虑，进而建立了该问题的期望值模型；

(2)提出了一种将随机模糊变量的密度函数等价转换为具有概率性质的密度函数的方法来求解该模型；

(3)应用该算法在实例中进行了有效的求解，得到了优化方案，说明了算法的有效性和合理性。

[1]马锦娟, 姚晓鹏, 郑挺. 非标准形式的指派模型在资源分配问题中的应用[J]. 大学数学, 2014, 30(06):17-20.

[2]魏阳. 航班计划中机型指派问题研究[D]. 成都:西南交通大学, 2014.

[3]李元左, 杨晓段. 指派问题的改进算法[J]. 价值工程, 2015, 34(07):303-304.

[4]朱明放, 叶飞跃, 丁小未. 基于GEP的任务指派问题的求解算法[J]. 计算机工程与应用, 2014, 50(22):50-53.

[5]关静, 张晓斌, 张金凤. 随机机会约束的机型指派模型及算法[J]. 山东大学学报(理学版), 2015, 50(03):45-51.

[6]肖继先, 李淑娟, 寇春蕾. 不确定机会约束规划模型及在TPTCL中的应用[J]. 物流工程与管理, 2014, 36(02):48-49.

[7]刘宝碇,赵瑞清.不确定规划及应用[M].北京:清华大学出版社,2003.

[8]李想.机会测度及其应用[D].北京:清华大学,2008.

Research and Application of Assignment Model under Double Uncertainty Environment

XIAO Ji-xian, KOU Chun-lei

(College of Science, North China University of Science and Technology, Tangshan Hebei 063009, China)

random fuzzy variable; assignment problem; expected value; equivalent transformation

In the assignment problem, the resource limitation was taken into consideration, and multi-objective assignment problem model with double uncertainly variable was built. A kind of equivalent transformation method was designed to solve the model, that is the density function of the random fuzzy variables was transformed into one function in the nature of probability density, and that the expected value of random fuzzy variable was calculated. And in this paper the method was verified by numerical example. The rationality and feasibility of the method were moved.

2095-2716(2016)01-0013-06

2015-09-29

2015-12-10

O221.6

A