GPS数据的单点测量不确定度评定

赵睿，杨久东

(华北理工大学 矿业工程学院，唐山 060039)



GPS数据的单点测量不确定度评定

赵睿，杨久东

(华北理工大学 矿业工程学院，唐山 060039)

GPS单点定位；误差来源；不确定度

以传统测量不确定度评定方法为基础，对GPS数据的单点测量误差来源进行了研究和分析，针对唐山市乐亭县D级控制网单点定位数据进行研究，并对其不确定度进行了评定。

长期以来，测量工作中一直存在测不准的问题，对于GPS单点定位测量亦是如此，由于各种误差影响因素的存在，难以获得站星之间的准确距离，因此对于一个完整的GPS单点定位结果应该包含测站点的坐标及其不确定度[1]。通过对于文献的研究，发现目前国内学者对于GPS单点定位不确定度的研究仍然较少[2-4]，本文以唐山市乐亭县首级控制网为例，对其单点定位数据不确定度进行了评定。

在测量工作中，误差的产生不可避免。目前GPS单点定位精度一般使用经典误差理论进行评定[5]。但是经典误差理论基于利用测量值与真值之差获取的真误差来对测量的精度进行评定，由于在测量工作中真值一般难以获取，所以只能采用约定真值进行代替。不确定度摒弃了使用真值来获取真误差进行精度评定的方式，转而使用区间来表征真值所处的范围，这就打破了使用约定真值的局限性。另一方面目前GPS单点定位的精度评定依据来源于一些处理软件给出的平差报告，但是对于一些含有迭代功能的平差软件，并不能给出真实的精度，这就很容易导致一些误差被遗漏，从而使成果的使用者无法获得可靠的成果。因此提出一种合理的GPS单点定位不确定度评定标准十分必要。

1 GPS单点定位不确定度的来源

在GPS测量过程中存在很多影响因素，而导致不确定度产生的影响因素主要有以下几种：

(1)对测量过程对环境影响的认识不恰如其分或对环境的测量与控制不完善[6]；

在GPS测量过程中，当卫星信号穿越电离层时会受到正离子与自由电子影响而产生折射；而当卫星信号穿越对流层时会受到压力、大气湿度、尘埃和水蒸气等的影响同样会产生折射现象；卫星信号受到周围环境影响而产生的多路径效应；除此之外，地球潮汐和负荷潮等也会造成影响。这些影响都属于对环境影响认识不足[7-9]。

(2)测量仪器性能不足；

钟误差是造成GPS观测误差的首要因素，也是测量仪器性能不足造成的主要不确定度来源；除此之外，相对论效应和天线相位中心偏差等影响都属于测量仪器性能不足[10-11]。

(3)引入数据或其他参量的不确定度来源主要有广播星历误差。

2 不确定度计算

2.1 B类标准不确定度评定

在GPS观测的过程中会受到多种因素的影响，这些影响因素都会对定位的结果产生等效的距离偏差。目前被人们公认的GPS定位误差来源如下表。

表1 GPS定位误差

GPS单点定位中存在的各项误差在经过数据预处理的过程以后认为其残差为σsi，其中i表示来自卫星部分、信号传播、信号接收和其他影响等的第i种误差。

不确定度表示量值范围，是对真值存在范围的估计和推断。而测量结果的不确定度即被测量值的分散性量化后可认为是等效距离偏差，也就是被测量值与真值的距离差。理想情况下被测量值等于真值，但由于各种测量误差的存在，测得的每个被测量值也有差异，取最大的距离与理想情况的范围为其置信区间半宽度。

本文中利用误差产生的等效距离偏差表征不确定度，理想条件下可以认为测量值等于真值，此时距离偏差为零，但是实际情况下误差是不能消除的。

由表1，若取误差对测量影响最小的情况，等效距离偏差如下：

若取误差对测量影响最大的情况，等效距离偏差如下：

其中最大的等效距离偏差为置信区间半宽度，即半宽度为21.817 4。

取置信概率为95%，则不确定度B类评定结果为：

2.2 A类标准不确定度评定

本文引用河北省唐山市乐亭县首级控制网数据为例，进行数据分析检验。

该网按D级网布设，仪器采用为中海达V8型GPS接收机，共联测控制点24个，其中已知点6个，均有WGS-84成果。该网观测时，每时段同步观测时间均在80 min以上。

控制点“东海2280”分历元单点定位结果如图 1 所示。

图1 点“东海2280”分历元单点定位结果图

点“东海2280”单点定位卫星图如图2所示。

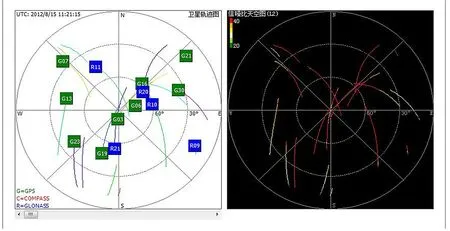
图2 点“东海2280”单点定位卫星图

Average Position X(m): -2393435.6211

Average Position Y(m): 4331338.2622

Average Position Z(m):4010398.3502

为避免人工输入错误及输出每个数据相对于平均值分布的偏差描点图，使用MATLAB对该点数据进行计算，得出结果如图3～5所示。

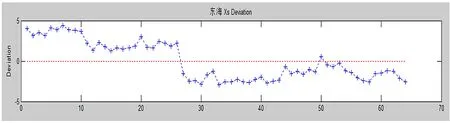
图3 坐标X的偏差描点图

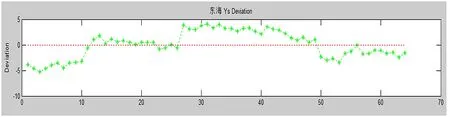
图4 坐标Y的偏差描点图

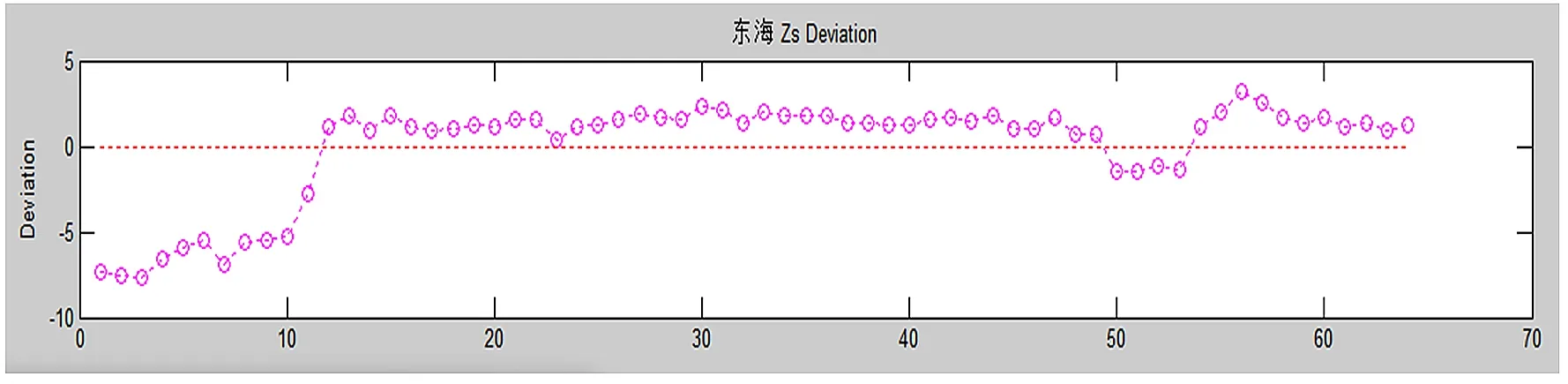
图5 坐标Z的偏差描点图

则该点的标准不确定度的A类评定结果为：

u(x)=s(xk)=2.354 6

u(y)=s(yk)=2.615 8

u(z)=s(zk)=2.950 2

将3个方向不确定度分量进行合成：

2.3 合成标准不确定度

根据JJF1059-2012《测量不确定度评定与表示》，可得合成不确定度为：

2.4 扩展不确定度

取置信概率为95%，此时包含因子为k=2，可得扩展不确定度为：

U=k·uc=23.672

3 不确定度检核

为了对得出的扩展不确定度准确性进行验证，利用HGO软件分别对控制网的已知点位分历元数据进行提取，并与已知坐标点位成果进行较差比较，将其结果统计于表2中。

表2 不确定度检核表

由表2可以得出检验数据中GPS单点定位最大误差为10.16，而测量不确定度评定得出最大单点定位误差为23.672，可以实现完全覆盖，由此证明利用上述方法获取GPS单点定位不确定度是可行的。

4 结论

(1)测量结果的不确定度即被测量值的分散性量化后可认为是等效距离偏差，由此计算GPS单点定位误差半宽度为21.817 4；

(2)通过对唐山市乐亭县D级控制网单点定位数据进行不确定度评定，研究了GPS单点定位数据的不确定度评定方法，得出其扩展不确定度为23.672。

[1]杨久东. 基于模糊集合的GPS测量不确定度理论与方法研究[D].北京:中国矿业大学(北京)，2014.

[2]林洪桦. 测量不确定度评定的熵方法[J]. 宇航计测技术，1997年增刊：20～27.

[3]林洪桦. 动态测量不确定A类评定[J]. 宇航计策计划，1996:117～122.

[4]许陇云，蔡榕钦. 动态不确定度的若干问题[J]. 宇航计测技术，1997年增刊：16～19.

[5]杨永平，兰孝奇，夏开旺. GPS(组合)伪距单点定位的精度研究[J]. 勘察科学技术，2006,06:31～34.

[6]赵春生. 测量不确定度的理论与实践研究[D]. 长春:长春理工大学，2007.

[7]杨天石. 多路径效应对GPS精密定位的影响及消除方法分析[J]. 勘察科学技术，2006,03:53～56.

[8]何玉晶. GPS电离层延迟改正及其扰动监测的分析研究[D]. 郑州:解放军信息工程大学，2006.

[9]丁晓光. 对流层延迟改正在GPS数据处理中的应用与研究[D]. 西安:长安大学，2009.

[10]游广芝. GPS导航定位中的误差分析与修正[D]. 哈尔滨:哈尔滨工业大学，2007.

[11]李鹏. GPS精密单点定位若干关键问题研究[D]. 成都:西南交通大学，2008.

Evaluation of Uncertainty of GPS Single Point Measurement

ZHAO Rui, YANG Jiu-dong

(College of Mining Engineering, North China University of Science and Technology, Tangshan Hebei 063009, China)

GPS single point positioning; error source; uncertainty

Based on the traditional evaluation method of measurement uncertainty, the error sources of the single point measurement of GPS data were studied and analyzed. The single point positioning data of D level control network in Laoting County of Tangshan were studied, and it's uncertainty was evaluated.

2095-2716(2016)01-0019-05

2015-09-17

2015-11-20

国家自然科学基金项目:(51404086)

P2

A