基于SVD的地震资料去噪方法的研究和应用
2016-12-19崔少华赵庆平
崔少华,单 巍,赵庆平
(淮北师范大学 物理与电子信息学院,安徽 淮北235000)
基于SVD的地震资料去噪方法的研究和应用
崔少华,单 巍,赵庆平
(淮北师范大学 物理与电子信息学院,安徽 淮北235000)
利用信号和噪声奇异值大小的差异,实现了奇异值分解算法去噪,通过对地震数据矩阵进行分解,得到按降序排列的奇异值矩阵,再选取与信号空间维数相同的奇异值个数进行重构,可以完全地恢复信号.采用两条同相轴地震数据进行验证,奇异值分解对于水平的或接近水平的同相轴去噪效果良好,对于倾斜的或弯曲的同相轴去噪效果欠佳,只有选取足够的空间维数才可达到预期去噪效果.
奇异值分解;地震数据;信号空间维数
对地震资料进行噪声衰减,提高信噪比,是地震资料中关键的一项任务,其中噪声的衰减通常是利用有用信号和噪声特性上的差异来进行分离,后续再对噪声进行去除.各种去噪方法也是根据噪声的特性不同而决定的.但实际地震资料中往往掺杂着与有效信号相互独立的噪声,也存在与有效信号相关的多次波的反射等干扰,在信号与噪声频率的特性不明显的情况下,分离噪声使用传统的频率域内滤波显然是无法进行的[1].因此,奇异值分解算法(Singular Value Decomposition,SVD)就是在这种情况下产生的.
在实际地震资料中,SVD算法被广泛应用于数据压缩和随机噪声的压制等方面,并且在这些方面的应用,奇异值分解有明显的作用.
1 SVD的方法原理
1.1 SVD的原理
设矩阵X是由m个通道观察值(每个通道上n点采样数据)组成的数据阵.由数学知识可知,当矩阵X满足一定条件时,可对X作如下分解变换[2]:
(1)
式中:U与V都是正交归一阵,即:
UTU=UTU=Im,
VTV=VVT=In(其中I表示单位矩阵).
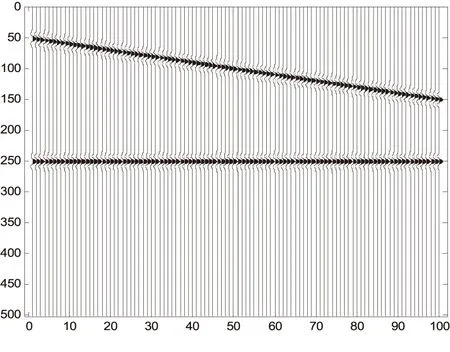
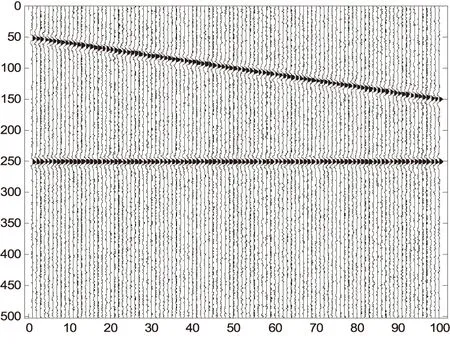
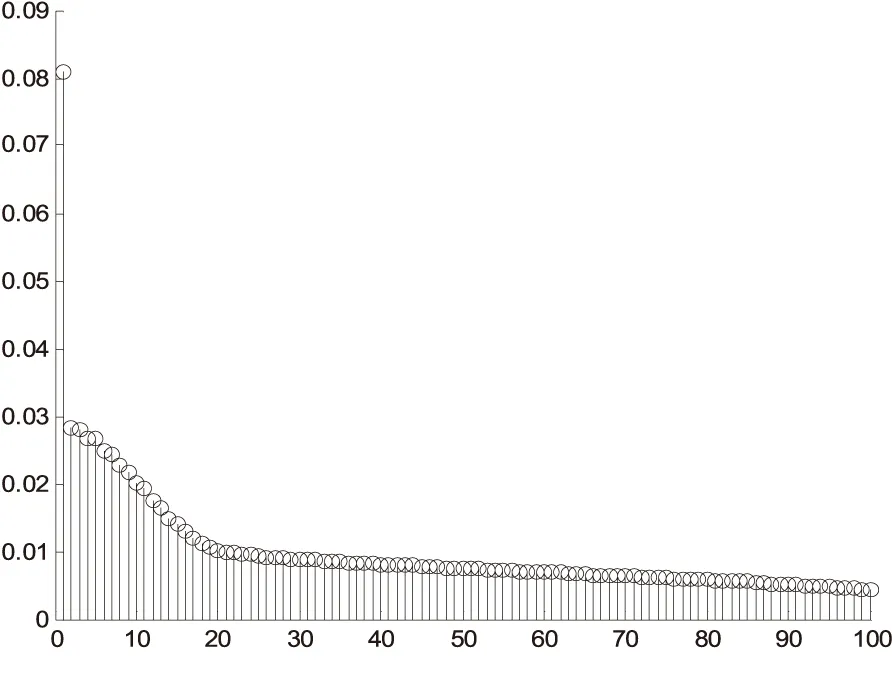
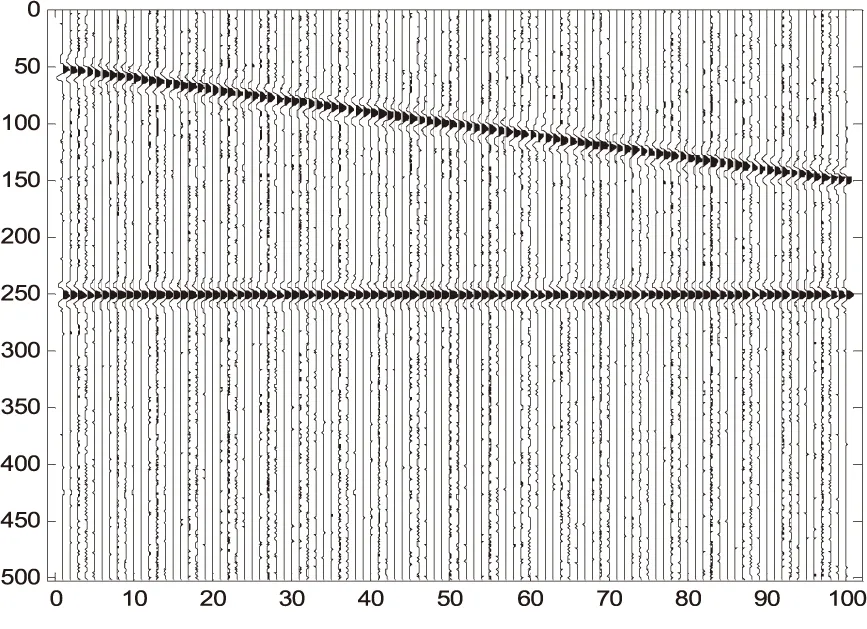
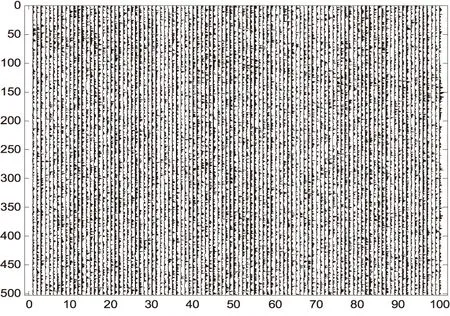
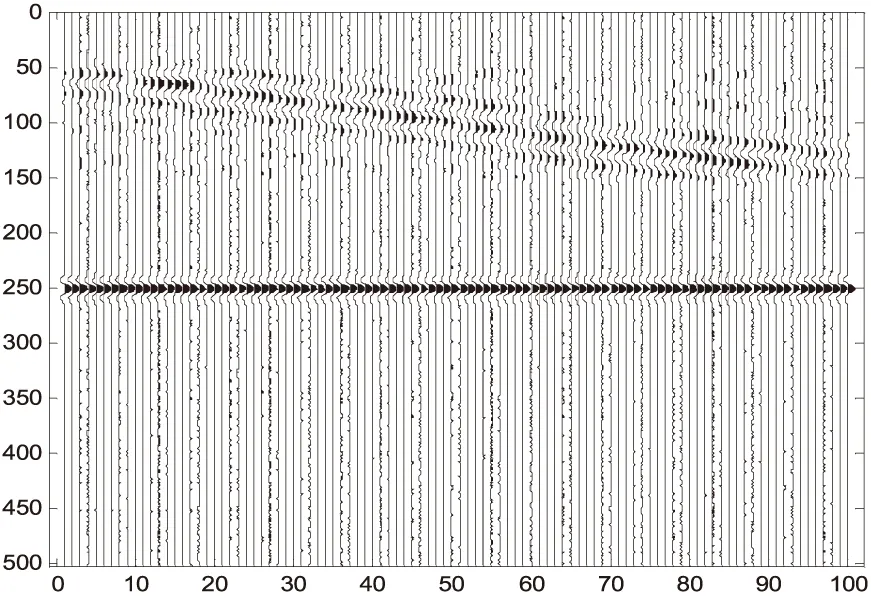
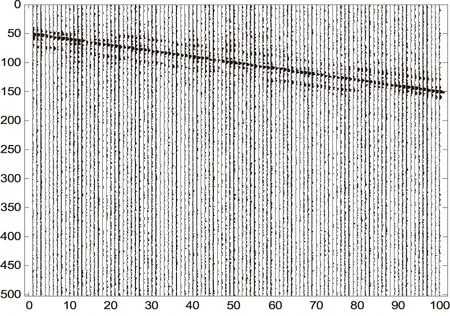
∑为准对角矩阵,在m (2) 通常设σ1≥σ2≥…≥σm≥0,称σi为奇异值. 如果记U=[u1,u2,…,um],V=[v1,v2,…,vn],则式(1)可写为: (3) 式中:ui和vi称为左、右奇异矢量,其维数分别为m×1和n×1.维数为m×n的原始数据就被分解成维数相同的m个子矩阵,这就是奇异值分解[3]. 1.2 SVD去噪方法 假设存在一个二维的地震数据X,其有m道观察值,每道有n个采样点数据(m (4) 接着在对X进行奇异值分解,利用式(1)可得: (5) 式中:U,V分别为左右奇异矩阵,∑为奇异值矩阵. 由式(4)和奇异值分解σ1≥σ2≥…≥σm≥0的性质,可以将式(5)用另一种方式表达: (6) 在奇异值矩阵中,∑S=diag[σ1,σ2,…,σp]就是地震记录中信号矩阵的奇异值,∑N=diag[σp+1,σp+2,…,σm]就是地震记录中噪声矩阵的奇异值. 其中p=Rank(S)就是信号矩阵的秩,即信号空间的维数[7].因此,为了完全保真有效信号,就必须进行不小于p阶的重构,将矩阵X的奇异值截断,舍去噪声空间的奇异值,进行P阶的重构就可完全恢复信号[8]: (7) 本次地震模型使用2条同相轴,其中1条水平同相轴,1条倾斜同相轴,地震子波采用峰值频率为50Hz的Ricker子波,时域每道501个点共100道,采样间隔1毫秒,结果如下图所示. 图1 原始二维地震记录 图2 含噪地震记录 图3 归一化奇异值曲线 由图3可知,第一个奇异值幅度远远大于其他奇异值,这实际上就是水平同相轴对应的奇异值.从第2到17个奇异值幅度明显下降,且幅度都远大于后面的奇异值,从18到100个奇异值,其变换缓慢,且幅度基本保持不变,因此,认为第1到17都是信号所对应的奇异值,从18到100个奇异值,是噪声对应的奇异值,对该记录进行17阶重构,结果如下图所示. 图4 17阶重构后结果 由图4可知,通过17阶的重构,可以将信号完全无失真地重构出来,在分离出来的噪声中,几乎不含有信号的能量,这一点也说明了,SVD只要选择正确的信号空间维数,对其进行重构后,可以很好地分离噪声,提高地震资料中的信噪比. 图5 17阶分离出噪声 针对本次模型,使用前6个奇异值重构后,结果如下图所示. 图6 6阶重构后结果 图7 6阶分离出噪声 由图6、图7可知,6阶重构将水平同相轴无失真地重构出来,将倾斜同相轴一部分重构出来,另一部分混合在噪声里,无法将其和噪声分离.已知该地震原始记录的信号空间维数为17,因此当重构信号空间维数取得不够时,无法完全重构非水平同相轴. SVD对水平同相轴的去噪效果优于对倾斜同相轴的去噪效果,甚至十分明显.SVD利用了有效信号各道之间的相关性,各道数据之间相关性越强,奇异值分解后信号的能量就越集中,信号和噪声就越好分离;反之,信噪可分性就较差.对水平同相轴,各道之间的相关性很强,往往只需要前面很少的几个奇异值就可以完全恢复,并且随机噪声大量地被压制;但是非水平同相轴(相关性减弱)却往往需要较多的奇异值才能完全恢复,并且在恢复的过程中,引入较多的随机噪声. [1]沈鸿雁,李庆春.线性域SVD地震波场分离与去噪方法[J].煤炭学报,2012,37(4):627-633. [2]朱萍萍,李双东,韩钰.广义正定矩阵的相关性质及其判定[J].通化师范学院学报,2015(6):26-27. [3]崔业勤,高建国,丁国超.LLE重构和SVD分解的地震信号降噪方法[J].计算机工程与应用,2015. [4]沈鸿雁,李庆春.奇异值分解地震纵、横波波场分离与去噪方法[J].石油地球物理勘探,2012,47(5):690-697. [5]彭更新,邓晓东,满益志,等.f-x域Cadzow滤波随机噪声衰减及其局限性分析[J].石油天然气学报,2013,35(1):63-66. [6]马继涛,王建花,刘国昌.基于频率域奇异值分解的地震数据插值去噪方法研究[J].石油物探,2016(2). [7]袁恩辉,陈凤来,齐志斌,等.奇异值分解在去除特殊干扰波中的研究与应用[J].非常规油气,2015,2(5):20-25. [8]何希平,杨劲,刘波.信号的SVD重建模型及其应用[J].计算机工程与设计,2015(4):962-966. (责任编辑:王海波) 10.13877/j.cnki.cn22-1284.2016.08.020 2016-06-14 安徽省高等学校自然科学研究项目(KJ2014B07) 崔少华,女,陕西咸阳人,讲师. P315 A 1008-7974(2016)04-0060-03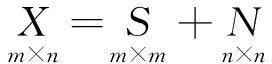
2 SVD去噪方法的应用
3 结论
