利率期限结构模型研究与实证分析

2016-12-19唐璟宜文忠桥

通化师范学院学报 2016年8期

关键词：样条国债期限

唐璟宜，文忠桥

(安徽财经大学金融学院，安徽蚌埠 233030)

利率期限结构模型研究与实证分析

唐璟宜，文忠桥

(安徽财经大学金融学院，安徽蚌埠 233030)

利率是传统意义上的货币价值，研究利率的期限结构有助于投资者对投资策略和方向有一个全局整体的把握，尤其是对于债券的投资．本文对我国的利率期限结构的理论和拟合方法进行简介，并结合实际数据，重点对四个认可程度广泛的利率期限结构进行拟合．利用MATLAB软件运行得出结果，并比较四种利率期限结构的优劣．

利率期限结构；多项式样条模型；指数模型；NS模型；NSS模型；实证分析

在金融市场上，资产种类和期限的不同会造成不同的利率，不同时点下的利率水平会形成一条利率曲线，即利率期限结构．利率期限结构有效反映了经济运行方面的基本信息，因此在我国积极推进利率和汇率市场化改革的宏观背景下，对我国的利率期限结构进行研究并准确把握其基本特征，对研究金融市场有重要意义．利率结构理论具有广泛的应用性．在宏观层面，由于利率期限结构与宏观经济运行、各类经济政策和金融现象密切相关，所以它既是联系实体经济和名义货币的中介，又是调节经济的杠杆．在微观层面，几乎所有成熟的固定收益定价模型都是以在一个无违约风险且仅反映系统风险的利率期限结构上加入风险溢价为逻辑而进行的，因此精确的利率期限结构是固定收益率金融资产定价等微观金融领域不可或缺的金融工具．

1 我国现有的国债利率期限结构的拟合估计模型

我国公认的国债利率期限结构拟合估计模型有：①多项式样条函数模型；②指数样条函数模型；③Nelson-Siegel(NS)模型；④Nelson-Siegel-Svensson(NSS)扩展模型．

本文的目的是对现有的四种模型进行实证分析，比较各自的优劣及差别，更加深入地了解国债利率期限结构拟合估计模型，从而为今后的学习以及应用奠定基础．

2 四种模型的实证分析

本文利用MATLAB软件，选取2015年11月11号当天的我国国债证券市场的实际数据，并筛选掉固定单利以及到期收益率为负的债券，得到共179项国债数据．对这些数据建立利率期限结构模型，分别使用四种样条函数进行利率期限结构的拟合，得到各自拟合结果函数和图像．

2.1 多项式样条函数

综合考虑拟合的平稳性以及先前的拟合经验，该函数选取5年和15年作为分界点，将利率期限结构划分为短、中、长三个时期，并构造三次样条函数为

B(0,s)=

约束条件为(保证分段点的连续性)，即

将约束条件代入原方程，简化模型参数得到新的函数方程组为

B(0,s)=

待估参数可由12个降低到5个．

β=(a1,b1,c1,a2,a3)=

(-0.024,-0.002,0.000,-0.000,0.000)

即得到实际方程组为

B(0,s)=

利用MATLAB做出多项式样条的利率期限结构图像，如图1所示：

图1 多项式样条模型的国债利率期限结构

从图1可以看出，根据多项式样条函数拟合出来的利率期限结构曲线较为平滑，性质优良．同理论一致，债券期限结构是随着到期期限的增加而上升的．到期期限越长，投资者就越要求回报率．按不同到期期限进行分析，可以看出对于短期债券(0-5年)，即期利率有明显上升趋势；而中间期限长度(5-15年)则表现得相对稳定，上升的速度有所减缓．长期国债的即期利率要高于短期国债，根据预期理论可以解释为：投资者预期未来即期利率上升，而市场分割理论则认为：长期债券流动性较之短期债券流动性差，对于长期债券要获得更高的流动性溢价．综合来看，曲线平滑且拟合优度较好，即采用多项式样条函数来估计国债利率期限结构曲线效果优良．多项式样条函数适用于研究结构的基本形状，还可据此来推测未来利率的变化情况．

2.2 指数样条函数

本文拟合指数样条函数时以3年和8年作为分界点，将利率期限结构时期划分为短期、中期、长期总共三个时期，并构造三次指数样条函数，基本形式为

B(0,s)=

约束条件仍需保证分段点的连续性．为减少待估参数，本文简化三次指数样条形式，有如下形式

B(0,s)=

此时方程中只有7个待估参数，利用MATLAB带入实际求解，得出参数分别为

β=(a1,b1,c1,d1,a2,a3,u)=

(0.954 -0.008 -0.185 0.027 0.237 0.066 0.239)

带入指数样条方程组中，得出结果，并作出指数样条利率期限结构图,如图2所示.

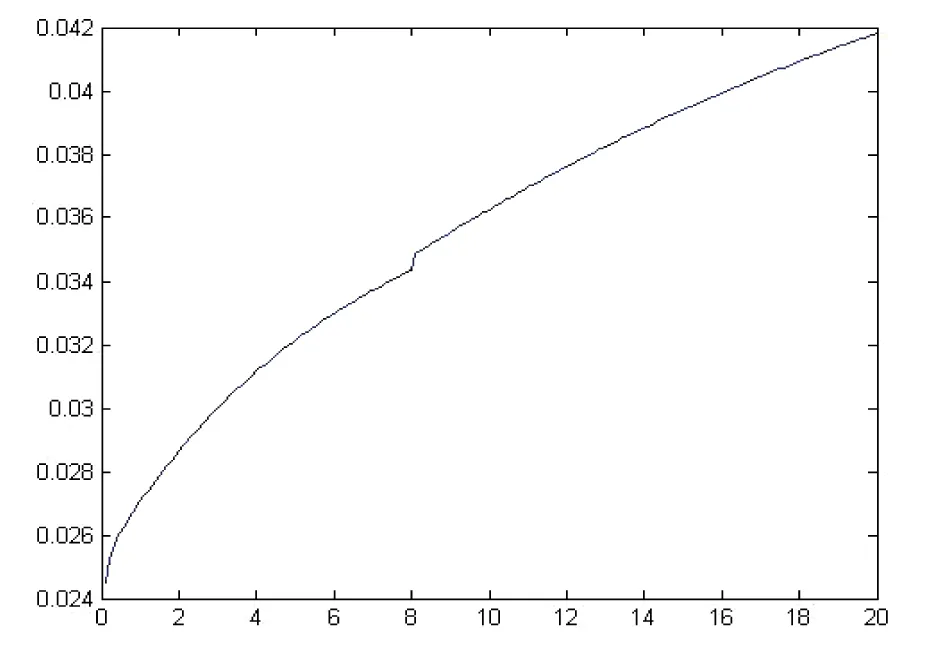
图2 指数样条模型的国债利率期限结构

从图2可以看出，图中分为两段，分别是0～8期与8～20期，说明短期和中长期具有相同的趋势.在0～8期，利率期限结构曲线平滑，并且曲线的上升势头很大，反映即期利率曲线在中短期内的斜率较大.在第8期时，到期收益率有一个垂直上拉的形态．从第8期开始到第20期，到期收益率起点并不是紧接上期的，而是比上期略大，这可能与当时的货币政策、利率政策等有关．在8～20期，利率期限结构曲线也是平滑上升的，但是上升的势头在接近20期时逐渐减缓，即期利率曲线在长期的斜率比短期斜率要小．总体而言，利率期限结构曲线的拟合效果较为优良，除了中间在8年期左右，短期利率向上突然上升一个高度，且其后维持不变，可能是由于某项政策的支持，对短期利率有一个补偿．

综上分析，指数样条同多项式样条的拟合结果相似，而指数样条的参数比多项式样条的参数估计要略微复杂．故一般情况下选择多项式样条法．

2.3 NS函数

一般指数形式的瞬时远期利率为

对应的即期利率函数为

此时方程中只有4个待估参数，利用MATLAB带入求解，得出参数为

β=(β1,β2,β3,m)=

(0.050 -0.025 0.002 0.126)

作出NS函数的利率期限结构图像，如图3所示.

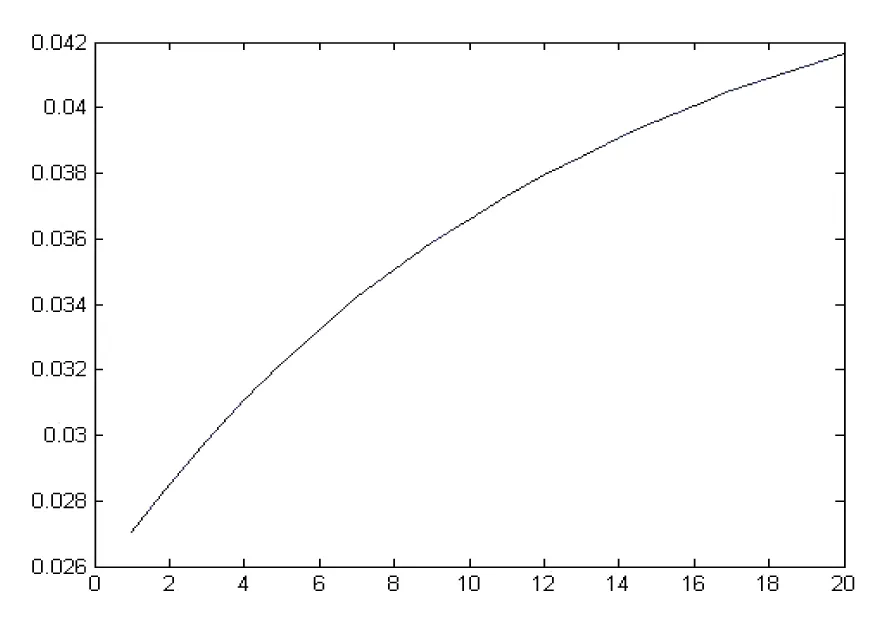
图3 NS模型的国债利率期限结构

从图3可以看出，NS模型的利率期限结构曲线的拟合优度良好，曲线平滑，并且即期利率曲线的斜率是逐渐减小的．由于我们的拟合期限较短，但根据现有趋势可以推测出在远期基本上处于一个水平的稳定状态．综合来看：NS模型所拟合的债券利率期限结构曲线比较平滑，且与根据多项式样条函数拟合的曲线更加接近，并且短期债券与长期债券的利率上升速度基本能够保持平稳，无突然的变化．

相比前面两种模型而言，NS模型对国债利率期限结构的拟合是最好的．该模型的优点是待估参数相对较少，因此适合在估计债券数量不多的情况下使用．而且参数有各自的经济含义,使得模型易于运用，便于理解．但是，NS模型也存在缺陷,如人为限定了曲线的形状,构造的曲线并不能完美贴合每一个样本点，在拟合的精度上仍有欠缺．

2.4 NSS函数

NSS模型可以解决NS模型刻画曲线种类受限的问题，其函数的构成相对而言更为复杂，其即期利率函数为

为了更好地拟合出利率期限结构，进行了两点改进.①增加中期项；②增加新的曲度参数和调整参数．

此时方程中仍存在6个待估参数，利用MATLAB带入实际求解，得出参数分别为

β=(β1.β2,β3,β4,τ1,τ2)=

(3.9943 -3.9701 -15.2991 0.0288 -0.0001 0.1316)

作出NSS函数的图像，如图4所示.

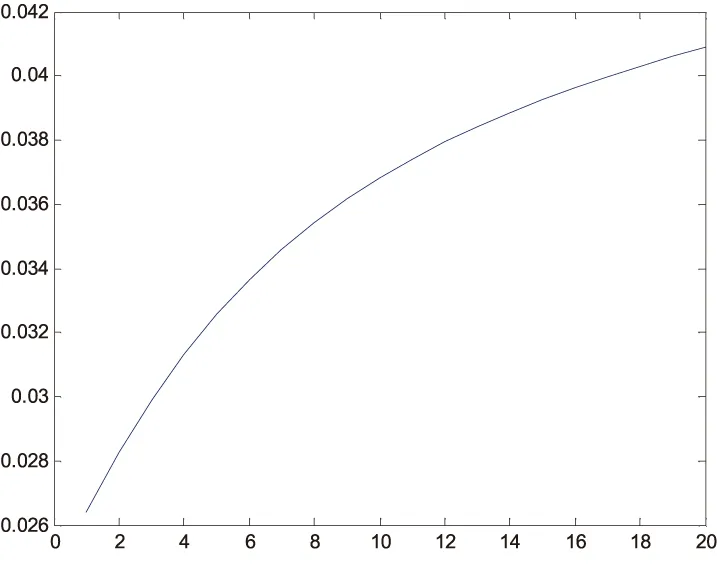
图4 NSS模型的国债利率期限结构

由图4看出，曲线还是很平滑的，对利率期限结构的拟合优度较好，利率期限结构图形是平滑上升的．根据NSS模型拟合的利率期限结构曲线与根据NS模型拟合的利率期限结构曲线几乎重合．它们的区别主要体现在拟合远端数据时有差别：以NS模型拟合的曲线在远端要更加发散一点．一般来说，以NSS扩展模型作为拟合利率期限结构的模型更合适，因为它可以用于描绘驼峰形和S形等复杂曲线．

3 四种模型的残差分析

作出四种模型的估计值与预测值的残差图，如图5所示，对此进行进一步模型评价．首先，寻找四幅图的相同之处．统一观察四幅残差图，可以发现其大体形状基本一致，均在第7个数据、第48个数据和第67个数据处存在较大误差，其余数据误差较小，仅存在轻微误差．根据各自的比例尺，发现多项式样条和NS函数的误差范围在[-20,20]之内，而指数样条和NSS函数的误差范围则略有增加，超过[-20,20]．接着本文试图寻找不同点．分别观察各自的波动幅度，可以初步得出指数样条和NSS函数的波动剧烈程度较大的结论．

图5 四种模型的残差

为了进一步比较四种模型的残差情况，本文用精确数据比较四种模型的残差均值以及波动情况,如表1所示．

表1 四种模型的残差均值以及波动情况

通过对实际数据进行分析，有以下结论：多项式样条的残差均值最小，但波动较大．指数样条的波动情况相对比多项式样条的波动情况小，当残差均值过大．NS函数与NSS函数的残差均值接近且均小于指数样条，而NSS函数的波动程度比NS函数的波动程度远大，且NS函数的波动率在四个模型的波动率中最小．综合以上分析，可以得出NS函数的估计最为合理且优良．

4 结论

综上，可以看出我国国债利率期限结构图形基本是呈右上方倾斜的，说明短中期利率普遍较低于长期利率．根据本文选取数据计算出四种模型的结果，有如下结论.①多项式样条函数和指数样条函数相比，前者对利率期限结构模型的拟合效果更好，因此在现实中可以在满足相同需求的情况下尽量使用多项式样条函数．②多项式样条法和NS模型所拟合的国债利率期限结构曲线都相对比较平滑，而指数样条法拟合的利率期限结构曲线则略微有些曲折．③多项式样条法拟合的即期利率曲线在远端是呈幂级数上升的，而指数样条法拟合的即期利率曲线在远端是比较平缓的．因此，指数样条模型更适合拟合长期数据．

在最后的残差分析中，NS 模型的拟合效果优于其他三种模型，这在某种程度上解释了为什么很多国家将 NS 模型运用于央行相关政策(货币政策、财政政策等)的制定．同时，由于本文的实证研究结果是基于我国国债收益率数据获得，说明了NS模型更适于我国国债利率期限结构的研究．

[1]李宏瑾.利率期限结构的远期利率预测作用[J].金融研究,2012(8):97-110.

[2]伍鹤.我国国债利率期限结构的比较研究[D].成都:西南财经大学,2007.

[3]沈鑫.中国宏观经济环境中的国债利率期限结构[D].天津:南开大学,2014.

[4]吕达劲.国债利率期限结构静态拟合及应用研究[D].成都:西南财经大学,2012.

[5]朱世武.交易所国债利率期限结构实证研究[J].金融研究,2003(10):63-73.

[6]李昊哲.基于指数样条函数的我国国债利率期限结构曲线的构造[D].长春:吉林大学,2010.

[7]文忠桥.中国银行间国债市场利率期限结构实证分析——基于Nelson-Siegel模型[J].财贸研究,2013(3):124-129.

[8]张启坤.基于NSS模型的利率期限结构影响因子的时间序列分析[J].赤峰学院学报,2014,30(6)：109-113.

[9]周子康,王宁,杨衡.中国国债利率期限结构模型研究与实证分析[J].金融研究,2008(3):131-149.

(责任编辑:陈衍峰)

10.13877/j.cnki.cn22-1284.2016.08.018