基于位移影响线曲率的小半径弯桥损伤识别

孙 珂, 张延庆

(北京工业大学 建筑工程学院,北京 100124)



基于位移影响线曲率的小半径弯桥损伤识别

孙 珂, 张延庆

(北京工业大学 建筑工程学院,北京 100124)

为了获取尽量全面的数据和减少对初始数据的依赖,在拟静力状态下测得弯梁桥竖向位移影响线(DIL),通过二次差分获得影响线的曲率.结合缺口平滑技术构造损伤指标,来实现对该类结构的损伤识别.以某三跨小半径弯梁桥为研究对象,建立相关数值模型来验证该方法的正确性及特点；对低速加载、支座预偏心及抗扭支座布置等对识别结果的影响进行分析.结果表明：对于小半径弯梁桥,该方法利用较少的测点,不依赖损伤前的数据,适用于多损伤识别；控制加载速度在一定范围内可以满足对损伤定位的需求；支点预偏心、设立抗扭支承等构造措施对损伤定位没有影响,损伤指标数值相对变小.

小半径弯梁桥；位移影响线(DIL)；曲率；损伤识别；缺口平滑技术

随着交通运输事业的发展,车辆载重加大,且数量日益增多,很多现役桥梁出现安全隐患,在较发达的地区已经进入了养护、改建为重点的阶段.在路线线形或城市立交互通的需求下,小半径弯梁桥占了相当的比重,明显的弯扭耦合作用使得结构受力和变形更加复杂[1].对使用状态的弯梁桥进行损伤识别及承载力评估研究,确保桥梁的使用条件,可以有效地保证弯梁桥的使用安全性和耐久性.

根据数据采集方法的不同,桥梁的损伤识别分为静力及动力测试方法.基于静力测试的桥梁结构损伤识别[2]是在桥梁停止使用的状态下对桥梁进行静载试验,具有测试数据准确、受噪音干扰小、简单等优点.基于动力测试的方法[3-5]一般是通过采集桥梁的振动响应信号处理得到频率和模态等数据来进行损伤识别分析.采用基于固有频率的损伤识别方法[3]虽然利用测量精度较高的固有频率,所测量到的结构固有频率的阶数有限,且对结构的局部损伤不敏感.利用静力测试数据的模型修正方法[4]和基于模态振型的损伤识别方法[5],为了获取结构较完整的响应数据,需要布置大量的传感器,这在实际工程中较难实现.

为了更全面地分析桥梁的工作状态,杜永峰等[6-7]提出采用拟静力状态下影响线加载的方式.影响线加载对于结构的选定截面具有全局性施加荷载的优点,能够反映在移动荷载作用下该截面响应的变化,克服了传统静力数据识别工况少,对局部损伤不敏感的缺点.随着工程测量技术(如GPS和激光技术等)的发展[8-9],利用较易得到的位移影响线数据分析结构工作状态已经成为可能[10],位移影响线的测试精度逐渐或已经满足损伤分析的需要.

上面这些对于桥梁的损伤分析方法一般都是对于直梁桥,更多的是简支梁桥.针对小半径弯梁桥受力变形特点的方法尚不多见.本文以某小半径连续弯梁桥为对象,由拟静力状态下测得控制点的竖向位移影响线,通过二次差分得到曲率曲线,结合缺口平滑技术以忽略对初始数据的依赖,对该结构进行局部损伤分析；针对低速加载、预偏心及中间设置抗扭支座等因素对损伤结果的影响进行探讨.

1 分析模型

一般来说,当弯桥的平面半径R<100 m时, 被称为小半径弯桥[11]；对于小半径弯梁桥的“弯扭耦合”作用更加明显,对抗扭性能的要求更高,受力变形更复杂.本文以某三等跨匝道弯桥为背景,该桥每跨跨度为30 m,R=60 m,桥型为混凝土箱梁桥,箱梁顶板宽12.5 m,底板宽6.5 m,翼板宽3 m.

图1 横截面示意图Fig.1 Cross section

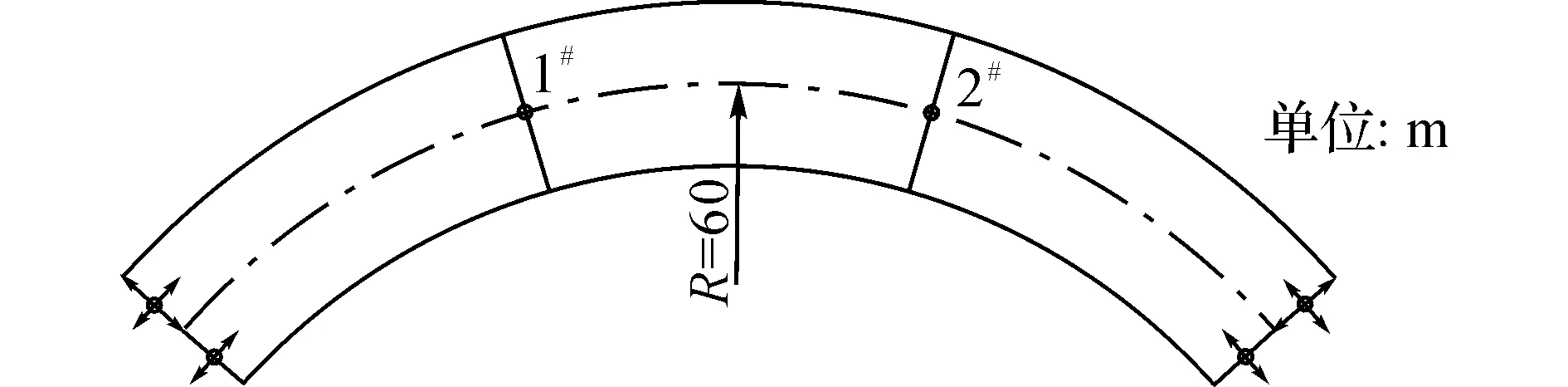
图2 平面布置及约束情况Fig.2 Sketch of bridge plan and support arrangement

主梁采用单箱双室截面,截面尺寸如图1所示.两端桥台按径向布置2个支座形成抗扭支承,两支座中心间距为3 m.该桥的平面布置及约束情况如图2所示.图中,箭头表示支座可活动方向,支座均约束竖向方向.弯梁桥材料采用C40混凝土,弹性模量为3.25×107kN/m2.

选用MIDAS有限元软件建立该结构的剪力-柔性梁格模型.该方法的原理主要如下：将实际结构的纵向刚度集中于纵向梁格内,横向刚度集中于横向梁格内；当原型实际结构和对应的等效梁格承受相同荷载时,两者的挠度近似相等,此时位移数据的计算精度满足本文分析的需要.根据上面的材料参数及截面形式建立相应的模型,关于其他因素的影响,如加载速度、支承条件等因素的参数选择,根据具体的分析内容给出.

2 数据拟合方法及损伤指标提出

获取某一点位移影响线的过程具有全局性加载的特点,可以利用一定的数值处理方法获得局部损伤处的刚度变化.杜永峰等[6]研究通过简支梁损伤前、后的位移影响线差值变化来进行损伤识别,对损伤前的数据依赖性大.为了减少对损伤前数据的依赖性,Ratcliffe[12]提出通过缺口平滑拟合方法,对损伤后一维梁的曲率模态进行平滑拟合,利用拟合曲线与损伤后曲线之间的差别来定位损伤位置.该方法简便易行,灵敏度较高,可以实现对局部损伤的识别.小半径弯梁桥需要考虑弯扭耦合作用对损伤识别结果的影响,也需要考虑桥横向不同位置的测点变形的规律.本文分别测取中心轴线上及径向同一截面上的不同测点数据来进行竖向位移影响线分析.

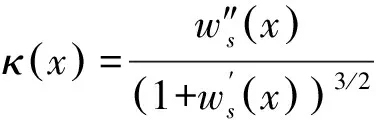
(1)

(2)

在工程或实验中,通过仪器测得某测点位移影响线后,需要利用数值分析原理的二阶数值微分公式来求解,此时相邻两点之间的间隔为d.对于任意连续平滑的位移影响线曲线ws(x),当xi-1,xi,xi+1之间的间隔d较小时,曲线在xi位置处的曲率数值可以用位移影响线上xi-1,xi,xi+1三点的数值表示,如下所示：

(3)

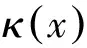
(4)

式中：a0～a3由前后相邻点xi-2、xi-1、xi+1、xi+2的数值曲率数值坐标确定的,即

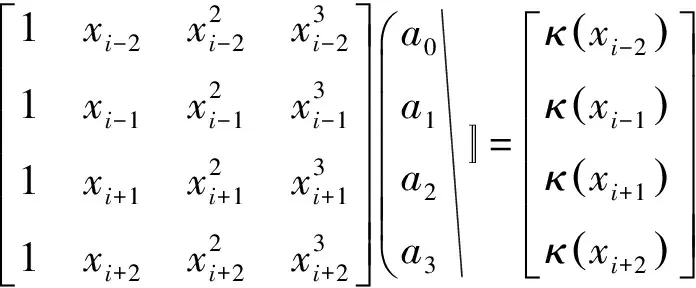
(5)

求解式(5)左端的矩阵的4阶范德蒙行列式不为0,式(5)的解存在,即利用下式判断：

(6)

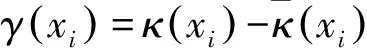
(7)

局部损伤识别步骤总结如下.选取小半径弯梁上的某点作为测点,通过荷载沿选定轴线加载来测得该点的一系列位移信息；利用式(3)处理得到该点的位移影响线曲率；利用式(4)～(6)得到拟合后的平滑曲率曲线；利用式(7)得到损伤指标,通过判断指标数值来实现对该结构的局部损伤识别.

3 小半径弯梁桥局部损伤分析

对于结构的局部损伤,文献[13]假定认为结构单元只引起单元刚度的下降而不引起单元质量的改变,在数值模拟计算中,用单元刚度的降低来模拟局部损伤.

3.1 损伤指标的验证

建立如图3所示的小半径连续弯梁桥.为了获得某点的位移影响线,加载荷载选择为550 kN,荷载沿着桥面中间轴线移动,此时中间支点未设置预偏心.

图3 弯梁桥模型Fig.3 Curved bridge model

如图3所示,先令第2跨在(9,10)m处的刚度折减20%,观测点选取该跨的跨中截面中点.首先观察损伤出现前、后竖向位移影响线的变化情况,图4(a)给出中间跨损伤前、后的跨中位移影响线,图4(b)给出影响线损伤前、后的差值Δws.以第2跨的中间轴线曲线坐标为基准,即以第2跨1#桥墩为坐标0点.

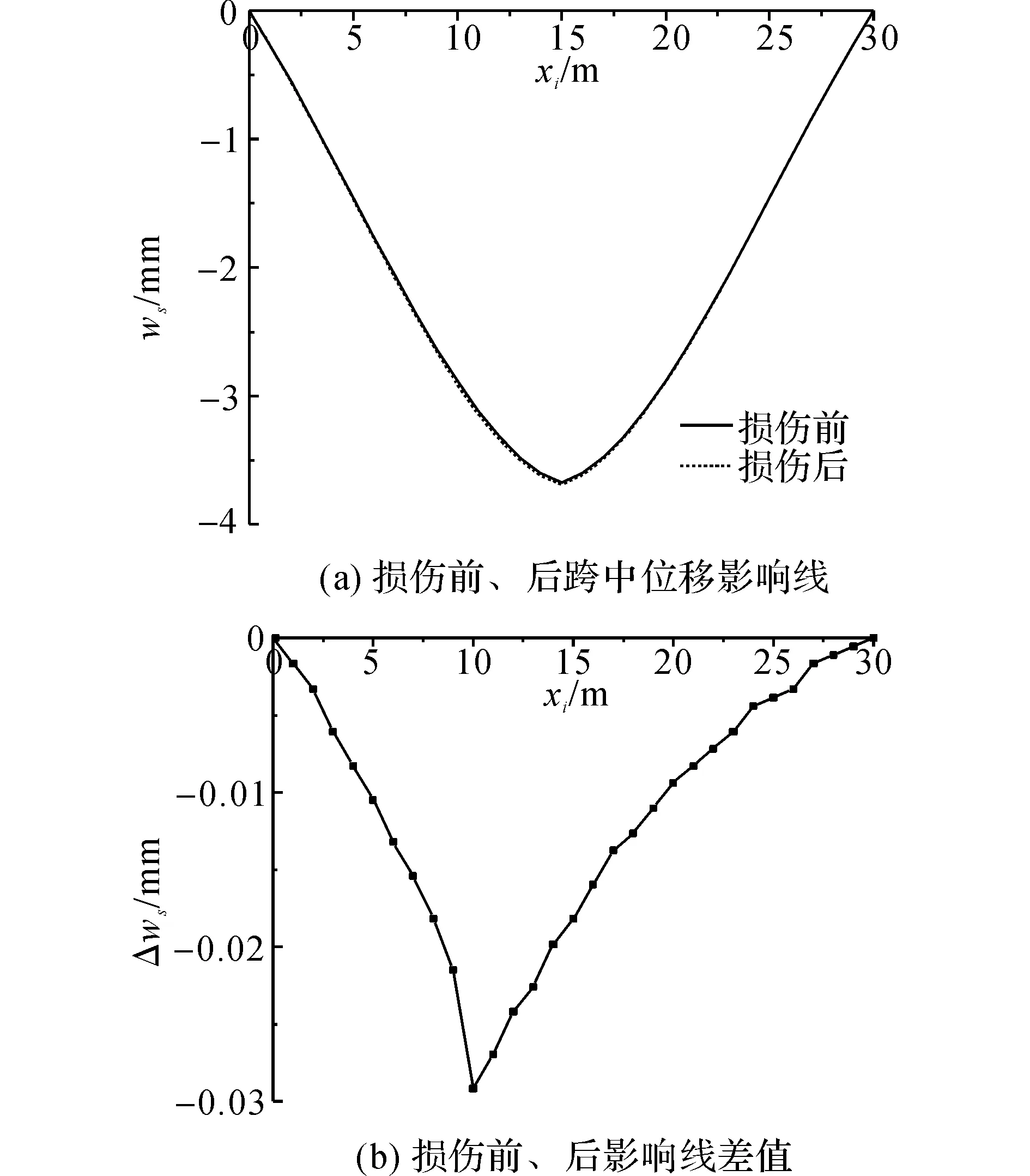
图4 损伤前、后位移影响线的比较Fig.4 Displacement influence line before and after damage

从图4(a)可以看出,当出现损伤时跨中位移影响线整体变大,但变化不明显；从图4(b)可以看出,损伤前、后位移影响线的差值在损伤区间(9,10)m处出现最大值.当缺少损伤前的数据后,结构很难直接从图形变化上给出损伤识别的结果.

不考虑损伤前的数据,利用式(3)对损伤后位移影响线数据进行处理得到曲率曲线,如图5所示.

图5 跨中测点位移影响线曲率Fig.5 Curvature of mid-span displacement influence line

从图5可以看出,当刚度折减20%时,位移影响线曲率在损伤区间(9,10)m处有一定的变化,证明选定测点的位移影响线曲率能够体现局部刚度的变化,但相对变化较不明显,尤其当损伤较小时很难体现.图5的曲率曲线在两端一定范围内出现负值,与两端的第1跨和第2跨刚度有关,不影响进一步观察分析.

利用跨中曲率曲线来进行损伤识别.结合相关曲率数值及式(6),可以求得式(5)的解是存在的,则可以得出该情况下的损伤指标,如图6所示.

图6 损伤指标γFig.6 Damage index γ

图6利用损伤识别过程进行处理,见式(4)～(6).从图6可以看出,在损伤位置(9,10)m附近指标γ出现明显变化,而在非损伤位置指标γ变化不大,通过该指标可以迅速地判断损伤位置,验证了该方法的可行性,即当存在单个局部损伤时利用该指标可以判断损伤的位置.

为了观察在损伤位置(9,10)m处出现不同损伤程度下的指标变化,图7给出当损伤位置刚度折减10%、20%、30%、40%时,损伤处指标数值的变化情况.图中，α为刚度折减系数.从图7可以看出,随着损伤的增大,损伤处指标数值增大,说明选择合适的参数,可以定量地判断损伤程度的变化.

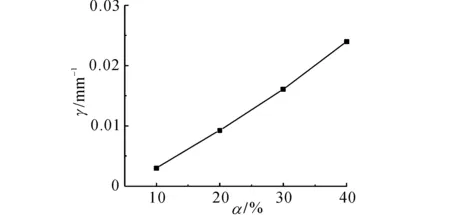
图7 不同损伤程度损伤区域指标变化Fig.7 Damage index changes at different degree ofdamage

分析多处局部损伤时该损伤识别方法的可行性.令第2跨在区间(9,10)m处刚度折减20%,区间(19,20)m处刚度折减10%.图8、9分别给出两损伤时的曲率曲线及损伤指标曲线.

图8 多损伤时位移影响线曲率Fig.8 Curvature of DIL with multi-damage

图9 多损伤时损伤指标γFig.9 Damage index γ with multi-damage

从图8可以看出,位移影响线的曲率曲线在两处损伤处均出现变化,在(9,10)m附近的变化明显大于(19,20)m处的变化.从图9可以看出,指标曲线在两处损伤的指标数值出现突变,说明该方法可以用作小半径连续弯梁桥的多损伤识别分析.

3.2 测点位置对小半径弯梁桥损伤识别的影响

从2个方面来分析不同测点对局部损伤结果的影响.首先考虑中心轴线上不同测点对局部损伤的识别效果；然后对于小半径弯梁桥,弯扭耦合作用使梁体内、外侧的受力存在差异,并影响梁体变形,须考虑选择径向同一截面不同测点对识别结果的影响.

令第2跨在区间(9,10)m处刚度折减20%.图10给出中心轴线上跨中(15 m)、三分之二跨(20 m)测点的损伤指标曲线.表1给出中心轴线上不同测点在损伤位置的损伤指标.

表1 不同轴向测点的损伤指标

图10 不同的轴向测点处损伤指标γFig.10 Damage index γ of point in the axis

从图10可以看出,选取不同测点不影响损伤定位,但由三分之二跨测点的位移影响线得到的损伤指标比跨中测点的指标小,即该损伤指标的数值与测点选择的位置有关.结合表1可以看出,对于该小半径弯梁桥第2跨来说,靠近损伤位置的12 m处测点损伤指标相对较大,在损伤处的指标数值随着测点远离损伤位置而逐渐减少.结合上面分析该损伤指标的大小与测点及损伤位置有关,一般来说,考虑到测量前损伤未知及测点的布置习惯,跨中测点的指标大小满足识别的需要.

为了比较影响线加载下梁体内、外侧的变形差异带给损伤识别的影响,图11给出跨中截面内、中、外3个测点的位移影响线曲率曲线,表2给出这3个测点损伤位置处的损伤指标.

图11 径向测点曲率曲线Fig.11 Curvature of points in horizontal

测点位置γ/mm-1内0．00462中0．00924外0．00440

从图11可以看出,出现损伤时内测点和外测点的位移影响线曲率整体数值变化趋势大致相同,在损伤处出现变化,可以利用本文提出的损伤指标；内测点的损伤指标稍大于外侧点,但这两个点的变化相对中测点的变化较小,结合表2可以看出内、外测点在损伤处的损伤指标比中测点小,即沿中间轴线加载时中测点得到的损伤指标更明显,更利于进行损伤识别.

4 损伤指标的影响因素分析

对于小半径连续弯梁桥,为了控制扭转效应,常常采用一些构造措施,如支座偏心、中间设置抗扭支座等,这些构造措施会影响受力变形的分配；为了测得某点的位移影响线,一般通过卡车慢车加载的方式,慢车加载的速度会对采集的数据有影响.针对以上这些情况,分析加载速度、支点预偏心及中间设置抗扭支座等因素对损伤指标的影响.

4.1 加载速度的对识别的影响

为了得到控制点的位移影响线,通过慢车加载[10],车辆低速加载会产生一定的动力效应,需要考虑不同加载速度对位移测量及损伤识别结果产生的影响.

在MIDAS软件中通过节点动力荷载的方式来模拟移动力加载,主要通过下列设定来实现.如图12所示,将移动力模拟为一个最大值为550 kN的三角形冲击荷载.图中,t0和t1以及t1和t2之间的时间差由荷载速度和节点间距来决定,可以用t1时刻表示荷载正好位于各节点上,其中分别模拟了低速为0.01、0.1、0.5、1、1.5、2 m/s的移动荷载加载；混凝土结构的阻尼比选为0.05.位移影响线取各节点t1时刻的测点数值,即取各节点在冲击荷载最大值时的测点位移.

图12 三角形冲击荷载Fig.12 Triangle impact load

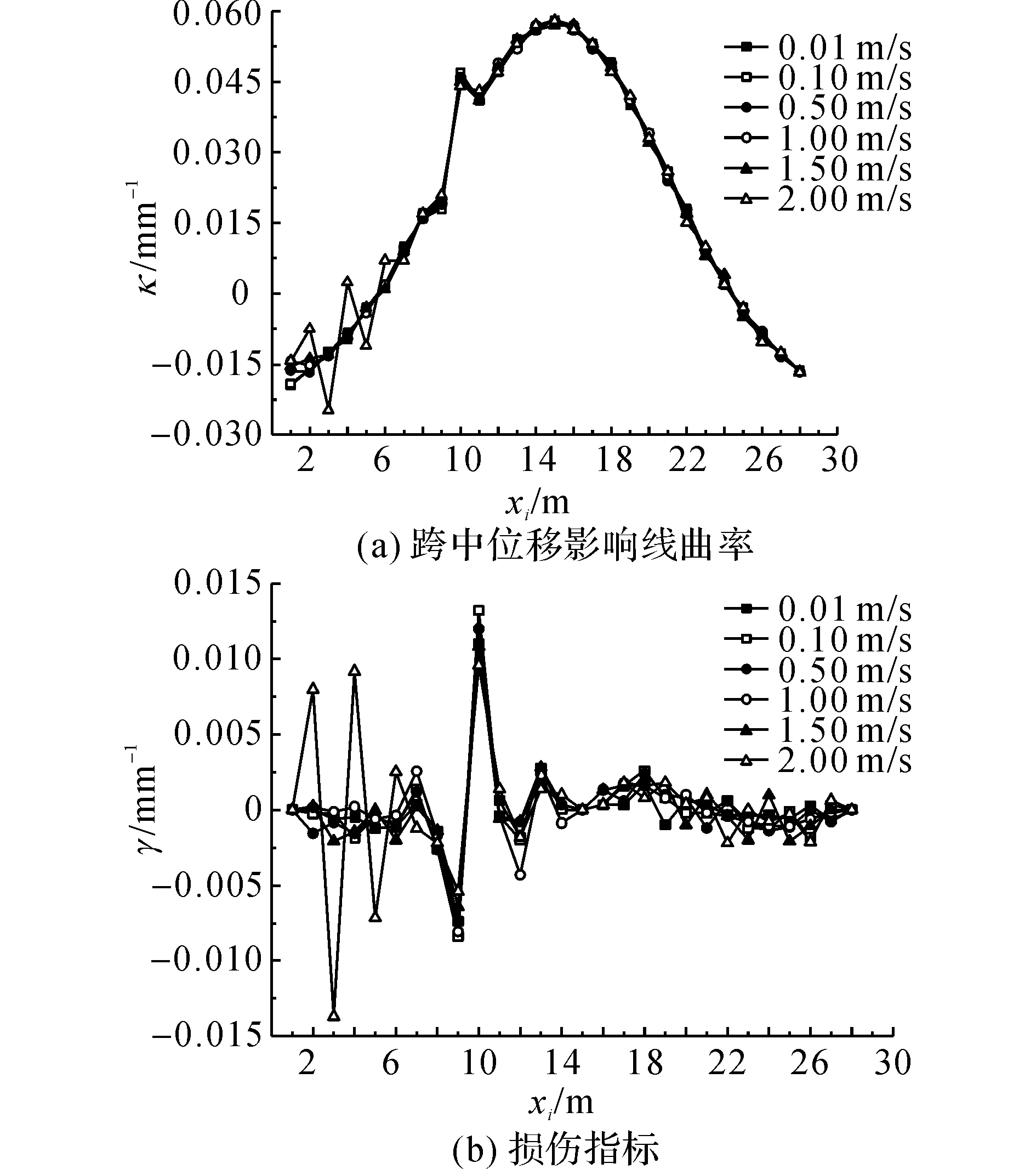
图13 不同加载速度下对识别结果的影响Fig.13 Effect on damage detection with different speed

选取第2跨中心轴线的跨中测点(15 m)；第2跨纵向区间(9,10)m范围内刚度折减20%.图13(a)给出这些速度下的跨中测点位移影响线曲率曲线,图13(b)给出损伤指标曲线.图中,xi选取第2跨的曲线轴向坐标.

从图13(a)可以看出,低速加载下的位移影响线曲率曲线在不同速度下的大致形状相同；当速度达到2 m/s时在非损伤区域出现波动,尤其是荷载位于梁端附近时.结合图13(b)可以看出,当速度达到2 m/s时,非损伤区域损伤指标出现大的波动,已经影响到损伤的识别.当速度在1.5 m/s以下时,对损伤指标的影响不大.

表3 不同速度下的损伤位置指标

Tab.3 Damage index with different speed at damageposition

v/(m·s-1)γ0．010．0110．10．0130．50．01210．0111．50．01120．010

表3给出不同荷载速度v时的损伤处指标γ.可以看出,随着加载速度的不同,损伤位置的指标数值出现变化.结合图13可知,通过低速的加载测量某控制点的影响线,加载速度在一定范围下会影响指标数值,但对损伤定位不会有影响,对于建立的模型结构,速度在1.5 m/s以下时损伤定位结果良好.

4.2 支点预偏心对识别的影响

对于该弯梁桥,中间独柱墩作为中支点,作用是减少弯曲长度,不能传递扭矩.设计时,为了调整梁内的扭矩分布,可以在各中墩的支点给以一定的横向预偏心[1,14],人为地控制沿梁跨方向梁内扭矩峰值,对位移影响线也有影响.为了观察支点预偏心对损伤识别的影响,选取第2跨的跨中截面横向的3个测点,在第2跨纵向区间(9,10)m内刚度折减20%,支座偏心e分别取0、0.1、0.2、0.3、0.4、0.5 m.图14(a)给出3种不同支座偏心下第2跨的跨中截面中点的变化,图14(b)给出不同偏心下跨中横向内、中、外3个测点在损伤处指标数值的变化.

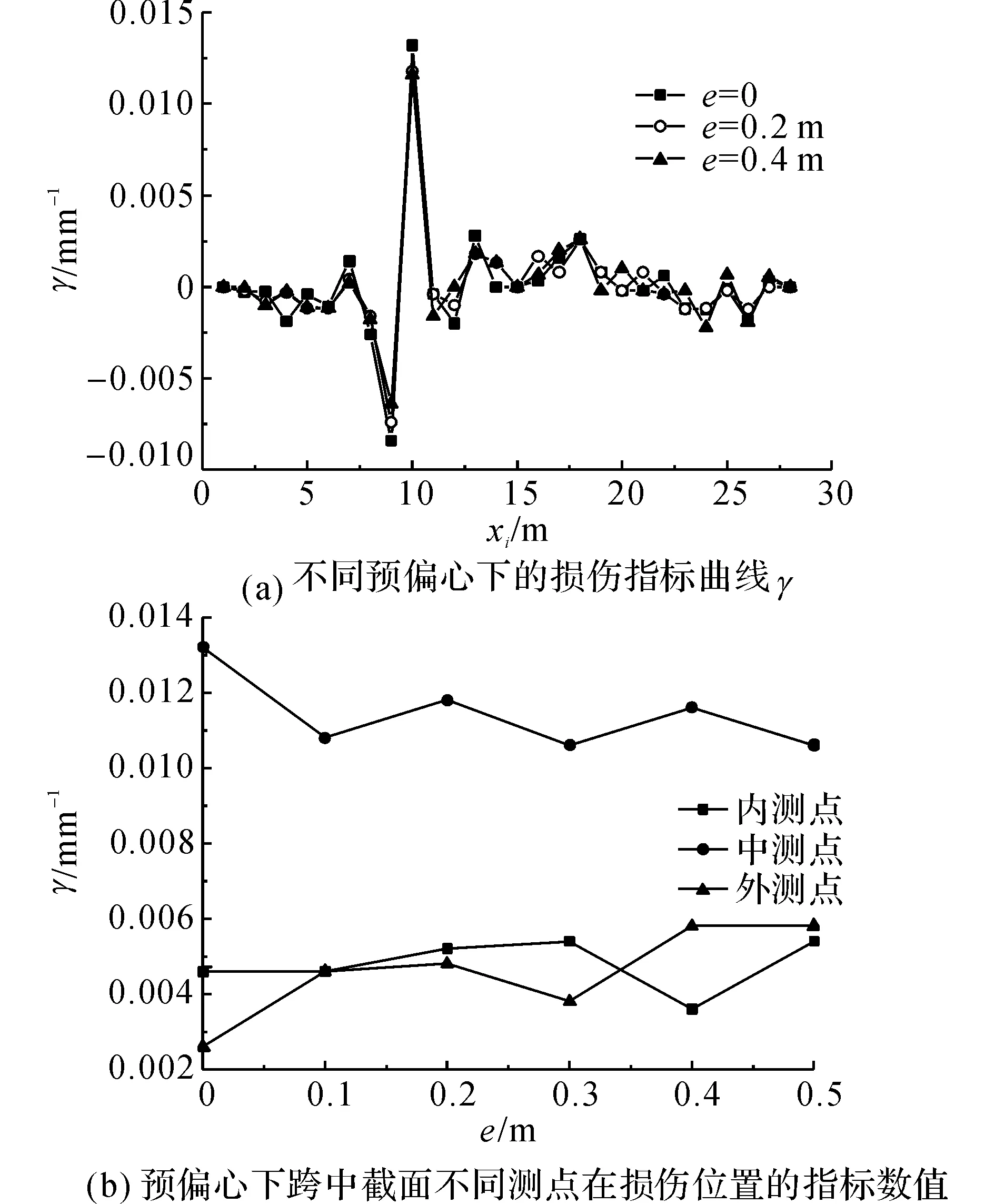
图14 不同预偏心对识别结果的影响Fig.14 Effect on γ with different pre-eccentricity

从图14(a)可以看出,偏心距离对于损伤的定位没有影响,整个指标曲线随着荷载位置的不同变化趋势一致,在损伤位置指标数值绝对值最大,发生突变；损伤处的指标随着与偏心的距离而发生变化,结合图14(b)可以看出,跨中横向上3个测点随着预偏心的不同,损伤处的指标数值发生变化,整体上横向中测点指标数值最大,该值在支点无预偏心时最大,随着预偏心的不同,损伤处指标数值最大相差20%,而内、外两个测点分别在不同预偏心下得到较大值.

4.3 中间设置抗扭支座

对于小半径弯梁桥,若中间支承处设置抗扭支座可以减少扭转跨度[1]和梁长方向的扭转峰值,影响整个结构的受力变形特性,同时抗扭支座之间的间距会影响梁体变形受力.分析抗扭支承的存在及抗扭支承的间距对损伤的识别,选取第2跨中心轴线的跨中横向的3个测点,在第2跨纵向区间(9,10)m内刚度折减20%,2#墩处通过布置2个支座实现抗扭支承,支座间距选取2.4、2.8、3.2、3.6、4.0 m.图15(a)给出2#墩处点铰支承和存在抗扭支承(支座间距为2.8 m)时的跨中截面中测点损伤指标曲线；图15(b)给出跨中横向各测点随着抗扭支座的间距D变化.

从图15(a)可以看出,当中间设置抗扭支承时,对损伤的定位没有影响,指标曲线的趋势大致相同,但设置抗扭支承时损伤指标数值较小.损伤处指标随着与抗扭支承的支座间距发生变化,结合图15(b)可以看出,跨中截面上3个测点随着支座间距的不同,损伤处指标数值发生变化,中测点指标数值最大,整体上中测点和外测点随着抗扭支承支座间距的变大,损伤指标数值变大,但损伤处指标数值都小于未设置抗扭支承时；内测点的指标数值随着抗扭支座布置的不同出现波动.

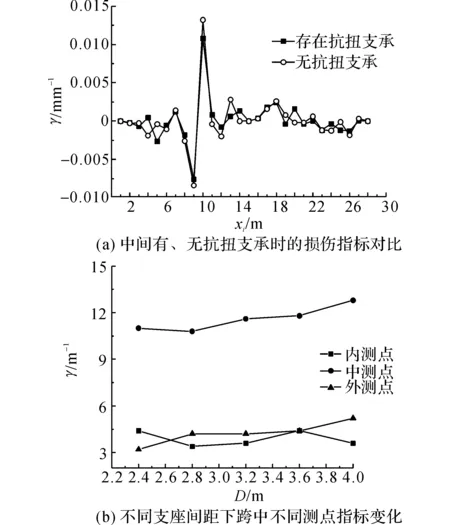
图15 中间布置抗扭支承对识别结果的影响Fig.15 Effect on damage detection with torsional bearing

5 结 论

(1)利用小半径连续弯梁桥控制点的位移影响线数据及二次差分得到曲率曲线,可以实现对局部的损伤识别,采用缺口平滑技术可以忽略对损伤前数据的依赖.损伤指标在损伤位置出现突变,不仅适用于单损伤识别,对多损伤识别也有良好的效果.

(2)对于测点的选择,损伤指标在损伤位置的数值与损伤位置、测点位置有关.当荷载沿着中心曲线轴线加载,在轴线方向布置测点时,一般跨中测点的损伤指标满足测量的要求；在跨中截面横向布置测点时,该截面中测点数值较大.

(3)为了获取拟静力状态的位移影响线,荷载移动速度(低速)的不同会对损伤结果及指标大小有影响.在一定的加载速度下,随着速度的不同,损伤指标数值出现变化,但不影响对损伤的定位.

(4)支点预偏心、中间设立抗扭支承等措施对弯梁桥损伤定位没有影响,但会影响指标数值,损伤处指标数值较未进行该措施时小.

[1] 邵容光,夏淦.混凝土弯梁桥[M].北京:人民交通出版社,1994: 16-49.

[2] 向天宇,赵人达,刘海波.基于静力测试数据的预应力混凝土连续梁结构损伤识别[J].土木工程学报, 2003,36(11): 79-82. XIANG Tian-yu, ZHAO Ren-da, LIU Hai-bo. Identification methods for different structural damage based on frequency response [J]. China Civil Engineering Journal, 2003, 36(11): 79-82.

[3] 谢峻,韩大建.一种改进的基于频率测量的结构损伤识别方法[J].工程力学,2004, 21(1)： 22-26. XIE Jun, HAN Da-jian. An improved method for structure damage detection based on frequency measurement [J]. Engineering Mechanics, 2004,21(1)： 22-26.

[4] 刘宇飞,辛克贵.移动荷载激励下基于平均曲率模态的简支梁局部损伤识别[J].工程力学, 2013, 30(7): 205-211. LIU Yu-fei, XIN Ke-gui. Local damage detection of simply supported beam on the excitation of moving load based on average curvature modal [J]. EngineeringMechanics, 2013,30(7)： 205-211.

[5] 荆龙江,项贻强.基于柔度矩阵法的大跨斜拉桥主梁的损伤识别[J].浙江大学学报：工学版, 2008, 42(1): 164-169. JING Long-jiang, XIANG Yi-qiang. Damage identification of main girders for long span cable-stayed bridge based on flexibility matrix [J]. Journal of Zhejiang University: Engineering Science, 2008,42(1): 164-169.

[6] 杜永峰,刘云帅,王晓琴.基于挠度差值影响线曲率的简支梁桥损伤识别[J].桥梁建设,2009, 38(4): 80-83. DU Yong-feng, LIU Yun-shuai, WANG Xiao-qin. Damage identification of simply-supported beam bridges based on influence line curvature of deflection differential values [J]. Bridge Construction, 2009, 38(4)： 80-83.

[7] ZHU S Y, CHEN Z W, CAI Q L, et al. Locate damage in long-span bridges based on stress influence lines and information fusion technique [J]. Advances in Structural Engineering, 2014, 17(8): 1089-1102.

[8] FUCHS P A, WASHER G A, CHASE S B, et al.Laser-based instrumentation for bridge load testing [J]. Journal of Performance of Constructed Facilities, 2004, 18(4): 213-219.

[9] ROBERTS G W, MENG X, DODSON A H. Integrating a global positioning system and accelerometers to monitor the deflection of bridges [J]. Journal of Bridge Engineering, 2004, 130(2): 65-72.

[10] HUANG J, SHENTON H W. Experimentally determined continuous displacement influence lines for bridges [C]∥Structures Congress 2008: Crossing Borders. Vancouver: ASCE, 2008: 1-10.

[11] 孙全胜,李茂奇.小半径曲线桥抗扭性能静载试验研究[J].公路,2009, 50(12): 43-47. SUN Quan-sheng, LI Mao-qi. Study of static load test and torsional properties of small radius curve bridge [J]. Highway, 2009, 50(12): 43-47.

[12] RATCLIFFE C P. Damage detection using a modified Laplacian operator on mode shape data [J]. Journal of Sound and Vibration, 1997, 204(3): 505-517.

[13] 李永梅,周锡元,高向宇,等.柔度曲率法对梁结构的损伤诊断[J].北京工业大学学报, 2008, 34(11): 1173-1178. LI Yong-mei, ZHOU Xi-yuan, GAO Xiang-yu, et al. Damage diagnosis of beam structures by flexibility curvature method [J]. Journal of Beijing University of Technology, 2008, 34 (11): 1173-1178.

[14] 滕军,胡渝,郭时安,等.高墩小半径曲线梁桥支点预偏心时力学性能分析[J].工程抗震与加固改造,2009,31(2): 9-15. TENG Jun, HU Yu, GUO Shi-an, et al. Mechanical characteristics analysis of small radius curve beam bridge with pivots pre-eccentricity with high piers [J]. Earthquake Resistant Engineering and Retrofitting, 2009, 31(2): 9-15.

Damage identification of small-radius curved bridge based on curvature of displacement influence line

SUN Ke, ZHANG Yan-qing

(CollegeofArchitectureandCivilEngineering,BeijingUniversityofTechnology,Beijing100124,China)

The vertical displacement influence line (DIL) of curved bridge at measuring point was measured in pseudo-static state in order to obtain as much as possible comprehensive data and reduce the demand of initial data. Curvature was calculated by the second order difference of DIL. Then a damage index was defined based on the gapped smoothing method. The validity of the method was verified by the relevant numerical model with a three span small-radius curved bridge as the background. The effects of the slow loading, bearing eccentricity, torsional bearing spacing and other factors on the damage identification were analyzed. Results show that for the small radius curved bridge, the method with less measuring points is suitable for multi damage identification that does not depend on the initial data. The damage location can be realized under a certain range of the loading speed. The measures such as bearing eccentricity, torsional bearing have no effect on the damage location, but the values of damage index are smaller.

small radius curved bridge; displacement influence line(DIL); curvature; damage identification; gapped smoothing method

2015-03-05. 浙江大学学报(工学版)网址： www.journals.zju.edu.cn/eng

国家自然科学基金面上项目(51378034).

孙珂(1987—),男,博士生,从事位移影响线的应用及弯桥损伤识别等研究. ORCID: 0000-0001-5438-3084. E-mail: sk.zll@163.com 通信联系人：张延庆,男,教授,博导. ORCID: 0000-0002-7635-9517. E-mail: zhyq@bjut.edu.cn

10.3785/j.issn.1008-973X.2016.04.018

U 441

A

1008-973X(2016)04-0727-08