基于方向密度检测与霍夫变换的混合矩阵估计
2016-12-19孙洁娣李玉霞温江涛闫盛楠
孙洁娣, 李玉霞, 温江涛, 闫盛楠
(1.燕山大学 信息科学与工程学院,河北,秦皇岛 066004;2.燕山大学 河北省测试计量技术及仪器重点实验室, 河北,秦皇岛 066004)
基于方向密度检测与霍夫变换的混合矩阵估计
孙洁娣1, 李玉霞1, 温江涛2, 闫盛楠1
(1.燕山大学 信息科学与工程学院,河北,秦皇岛 066004;2.燕山大学 河北省测试计量技术及仪器重点实验室, 河北,秦皇岛 066004)
针对欠定盲源分离混合矩阵的估计问题,提出一种基于局部方向密度检测的孤立时频点处理与霍夫变换相结合的混合矩阵估计算法. 首先通过变换域单源时频点处理增强信号的稀疏性,对散点图中的方向直线进行霍夫变换,通过判断局部极大值点确定源信号数量并估计混合矩阵. 针对霍夫变换易出现的峰值簇拥问题,提出采用局部方向密度检测方法先判别并去除孤立时频点,之后再进行霍夫变换,提高了混合矩阵的估计精度. 实验结果表明本文所提出的方法能够在未知源信号数量情况下实现混合矩阵估计,且估计精度高于K-means等常用方法.
欠定盲源分离;混合矩阵估计;霍夫变换;局部方向密度;孤立时频点
盲源分离(blind source separation,BSS)是指在源信号及传输信道参数均未知的情况下,根据输入源信号的统计特征,仅利用观测信号来恢复源信号的过程. 由于其在数字通信、语音识别和阵列信号处理等领域具有广泛的应用,近年来已成为研究热点. 对于观测信号数量少于源信号数量的欠定盲源分离(underdetermined blind source separation, UBSS)问题,目前研究较多的是稀疏分量分析(sparse component analysis,SCA)方法. SCA利用信号的稀疏特性,通常采用两步法:① 估计混合矩阵;② 恢复源信号. 其中混合矩阵的估计是实现欠定盲分离的重要步骤,估计精度会直接影响信号分离质量.
利用信号的稀疏性,Bofill等[1]提出基于势函数的欠定混合矩阵估计算方法,但是此方法对势函数的参数选择缺乏理论指导. 付宁等[2]将K-means聚类与霍夫变换结合估计混合矩阵,但K-means算法不仅依赖初始聚类中心的选择,还要预先知道源信号数量,无法处理源信号数量未知情况. 谭北海等[3]提出概率统计方法估计信号源的数量,但该方法不易扩展到高维空间,且对信号稀疏度[4-8]要求较高. 为了降低对信号稀疏度的要求,有学者提出了基于单源时频点[9-11]的方法增强信号稀疏性[12],但是存在定义方法多样,符合条件不易等问题.
本文针对传统聚类方法进行混合矩阵估计时,信号稀疏性不强,且依赖初始聚类中心的选择,以及需要预先设定源信号数量的不足,研究了基于孤立时频点检测与霍夫变换相结合的混合矩阵估计算法. 通过变换域中单源时频点处理增强信号的稀疏性;并采用霍夫变换将直线方向检测转化为变换空间中局部极值点检测,达到估计混合矩阵的目的. 针对霍夫变换产生的峰值簇拥问题,本文提出进一步去除孤立时频点来解决峰值簇拥问题.
1 单源时频点处理增强信号稀疏性
不考虑噪声影响的UBSS混合模型为
x(t)=As(t), t=1,2, …,T.
(1)
式中:x(t)=[x1(t)x2(t) …xm(t)]T为m个观测信号;A=[a1a2…an]为混合矩阵,A∈Rm×n;s(t)=[s1(t)s2(t) …sn(t)]T为n个未知的源信号;m (2) 由式(2)可得观测信号分布在过原点的直线上,直线的方向取决于混合矩阵的列向量ai,即稀疏信号具有线性聚类特征,并且线性聚类的强弱直接影响混合矩阵的估计精度. 大多数信号在变换域中具有稀疏性,本文主要研究变换域中的稀疏处理,对式(1)进行短时傅里叶变换(STFT),可得 (3) 式中:X(t,k)为观测信号的STFT系数;Si(t,k)为第i个源信号的STFT系数. 当稀疏性较弱的信号变换到时频域后,时频域中任一时频点上仅有一个源信号存在的点为有效时频点,称之为单源点. 本文研究采用单源点检测方法来进一步增强信号稀疏性. 设某时频点(t1,k1)处只有一个信号s1存在,此时式(3)表示为 X(t1,k1)=a1S1(t,k). (4) 取式(4)两边的实部R{·}和虚部I{·},由稀疏信号的线性聚类特性得R{X(t1,k1)}和I{X(t1,k1)},各分量比值均为a1. 若在时频点(t2,k2)处有多个源信号s1和s2存在,则观测向量的实部和虚部分别为 R{X(t2,k2)}=a1R{S1(t2,k2)}+a2R{S2(t2,k2)}. (5) I{X(t2,k2)}=a1I{S1(t2,k2)}+a2I{S2(t2,k2)}. (6) 若观测向量实部与虚部各分量比值相同,则 (7) 即需满足R{Xi}/I{Xi}=R{Xj}/I{Xj},其中i,j∈[1,m]且i≠j,式(7)成立的概率极低,考虑实际误差,设阈值ε范围为0.01~0.1[11],可得 (8) 式(8)即为单源点检测公式. 为克服低能量时频点的影响,根据式(9)过滤一些低能量点: (9) 式中λ∈(0,1). 经过上述处理后信号的稀疏性得到较大增强,为混合矩阵的估计提供了基础. 2.1 基于霍夫变换的方向直线转换 霍夫变换(Hough transform,HT)是一种实现从图形空间到参数空间转化的映射方法,它通过对图形空间中的对象进行坐标变换,将原始图形空间中给定曲线上的所有点都集中到变换空间上的某些位置,形成一系列局部累加值极大点. 假设原图形空间中经过点(x1,x2)的某一直线为:x2=ax1+b,通过坐标变换映射到变换空间ρ-θ中,转化成相应的极坐标形式为 ρ=x1sin θ+x2cos θ. (10) 则式(10)为点(x1,x2)的霍夫变换,其中θ为直线与x1轴的夹角,tanθ=x2/x1. 霍夫变换应用于混合矩阵估计中的思想为:将原始空间中共线的点经坐标变换转化为参数空间里相交的曲线,由于稀疏性的源信号具有线性聚类的特点,因此观测信号进行HT后在变换空间将形成一系列相交的曲线,统计曲线的交点并进行累加形成为局部极值点,统计所得的局部极值点数量即为源信号数量;通过检测极值点位置可以估计直线方向,即混合矩阵列向量,进而估计混合矩阵. 由于稀疏观测信号的线性聚类特性,观测数据点主要集中在n条直线上,则直线向量l表示为 ρ=lTx. (12) 由于HT算法统计的是变换空间中的局部极值点,在提取中常会出现峰值簇拥问题. 图1为单源时频点图及经过HT后统计的局部极值分布图. 由图1可知由于存在孤立点使得时频点线性聚类不够清晰,经过HT统计局部极值时,产生局部峰值簇拥问题,导致难以准确估计源信号数量. 2.2 基于方向密度检测孤立点的混合矩阵估计 局部峰值簇拥问题产生主要是由于该区域内时频点较少、线性聚类特性不清晰,且偏离混合矩阵列向量的主方向,因此可将这些无效的时频点称为孤立时频点. 本文研究了通过局部方向时频点密度检测方法去除孤立点,解决霍夫变换的峰值簇拥问题,提高源信号数量及混合矩阵估计精度. Di(φ)=N(Ci(φ))/N. (13) 对图1去除孤立点并进行HT结果如图2所示. 对比图1(b)与图2可知本文处理方法可以有效抑制峰值簇拥,准确估计源信号数量. 本文提出的基于局部方向时频点密度检测与霍夫变换的混合矩阵估计算法步骤如下: ① 通过STFT将观测信号变换到时频域; ② 检测单源时频点并去除低能量点,再将观测数据对称到上半单位超球面上并进行归一化; ③ 统计局部方向时频点密度去除孤立点; ④ 设置分辨率参数构成累加数组进行HT,统计累加数组的极值数量即为源信号数量,通过极值坐标参数得直线向量,即为混合矩阵A的列向量. 为验证本文算法的有效性,通过两个实验进行仿真与分析,并利用归一化均方误差(normalized mean square error,NMSE)及偏离角度两种指标评价混合矩阵估计性能. 归一化均方误差定义为 偏离角度表达式为 3.1 实验1及结果分析 实验1采用的源信号为3个不同的语音片段,按照式(1)将其混合成两路,随机选择A为 混合所得的观测信号如图3. 观测信号的时域与时频域散点图如图4所示. 由图可见时频域中观测信号方向性较弱,因此进行单源时频点处理增强信号稀疏性. 单源点检测时取ε=0.06,所得单源时频点如图5(a),通常λ范围为0.05~0.10[3],本文取λ=0.1,将数据归一化并进行HT,综合大量实验与实际情况,取β=180,则HT的局部极值分布如图5(b)所示. 单源点检测后观测信号的方向性变得比较清晰,但仍有少量孤立点导致峰值簇拥问题,影响源信号数量的估计,采用本文提出的局部方向时频点密度检测方法去除孤立点,取φ=1°;δ决定了去除数据点的多少,通常δ∈[min(Di(φ)),mean(Di(φ))],统计δ与剩余时频点所占比例如图6所示. 图6显示δ越大,剩余时频点比值越小,当比值趋于稳定时,表明已去除大部分孤立点,由图可得从δ=0.025开始该比值较稳定,因此取δ=0.025,则所得归一化散点图与HT结果如图7所示. 为了准确比较几种算法的估计精度,将估计矩阵与A的NMSE以及偏离角度的结果列入表1. 表1 估计的与初始A的性能对比表 由表1对比几种算法可得,去除孤立点能较大提高混合矩阵估计精度,解决峰值簇拥问题,验证了去除孤立点的必要性,并且HT算法能够在准确估计源信号数量基础上进一步提高混合矩阵估计精度. 实验结果表明本文算法的估计准确性更高. 3.2 实验2及结果分析 实验2采用的源信号为文献[1]中稀疏性较弱的语音信号,取数据长度为63 856的4段信号作为源信号,根据式(1)将其混合为3路观测信号,即m=3,n=4,随机选择混合矩阵A为 混合之后得到的观测信号如图8所示. 将观测信号变换到时频域后,检测单源点并归一化后直接进行HT,得到结果如图9所示. 针对峰值簇拥导致不能准确估计源信号数量问题,统计δ与剩余时频点所占比例选取δ=0.02,去除孤立点经HT后得到的结果如图10所示. 为了对比算法的性能,将估计的混合矩阵根据式(15)计算各个估计矩阵的NMSE,统计结果如表2所示. 表2 估计的与初始A的NMSE对比表 统计实验二的偏离角度的对比结果如表3. 表3 估计的与初始A的偏角对比表 分析仿真结果可知,将观测信号扩展到三维空间之后应用本文算法估计所得到混合矩阵精度得到较大提高. 通过以上不同算法的实验结果对比,能够有效验证去除孤立点的必要性,以及HT算法的优越性,说明本文所提算法的有效性. 实验结果表明,与常用的K-means聚类算法以及K-Hough算法比较,本文所提出的方法较大程度提高了混合矩阵估计精度. [1] Bofill P, Zibulevsky M. Underdetermined blind source separation using sparse representations[J]. Signal Processing, 2001,81(11):2353-2362. [2] 付宁,彭喜元.K-Hough欠定盲信道估计算法[J].电子测量与仪器学报,2008,22(5):63-67. Fu Ning, Peng Xiyuan. K-Hough underdetermined blind mixing model recovery algorithm[J]. Journal of Electronic Measurement and Instrument, 2008,22(5):63-67. (in Chinese) [3] 谭北海,谢胜利.基于源信号数目估计的欠定盲分离[J].电子与信息学报,2008,30(4):863-867. Tan Beihai, Xie Shengli. Underdetermined blind separation based on source signals’ number estimation[J]. Journal of Electronics & Information Technology, 2008,30(4):863-867. (in Chinese) [4] Zhou G X, Yang Z Y, Xie S L, et al. Mixing matrix estimation from sparse mixtures with unknown number of sources[J]. IEEE Transactions on Neural Networks, 2011,22(2):211-221. [5] Peng D Z, Xiang Y. Underdetermined blind sources separation based on relaxed sparsity condition of sources[J]. IEEE Transactions on Signal Processing, 2009,57(2):809-814. [6] Kim S G, Yoo C D. Underdetermined blind source separation based on subspace representation[J]. IEEE Transactions on Signal Processing, 2009,57(7):2604-2614. [7] Li Y Q, Amari S, Cichochi A, et al. Underdetermined blind source separation based on sparse representation[J]. IEEE Transactions on Signal Processing, 2006,54(2):423-437. [8] Bofill P. Identifying single source data for mixing matrix estimation in instantaneous blind source separation[C]∥Proceedings of 18th International Conference on Artificial Neural Networks. Prague, Czech Republic: Springer, 2008: 759-767. [9] Reju V G, Koh S N, Soon I Y. An algorithm for mixing matrix estimation in instantaneous blind source separation[J]. Signal Processing, 2009,89(9):1762-1773. [10] Dong T B, Lei Y K, Yang J S. An algorithm for underdetermined mixing matrix estimation[J]. Neurocomputing, 2013,104(15):26-34. [11] Xie S L, Yang L, Yang J M, et al. Time-frequency approach to underdetermined blind source separation[J]. IEEE Transactions on Neural Networks and Learning Systems, 2012,23(2):306-316. [12] Syed M N, Georgiev P G, Pardalos P M. A hierarchical approach for sparse source blind signal separation problem[J]. Computers& Operations Research, 2014,41:386-398. (责任编辑:刘芳) Mixing Matrix Estimation Based on Local Direction Density of Time-Frequency Coefficients and Hough Transform SUN Jie-di1, LI Yu-xia1, WEN Jiang-tao2, YAN Sheng-nan1 (1.School of Information Science and Engineering,Yanshan University, Qinhuangdao, Hebei 066004, China; 2.Key Laboratory of Measurement Technology and Instrumentation of Hebei Province, Yanshan University, Qinhuangdao, Hebei 066004, China) A mixing matrix estimation method based on local directional density of time-frequency coefficients and Hough transform was proposed for underdetermined blind source separation. The signals were transformed to time-frequency domain by STFT to improve sparsity; and then Hough transform was applied to transform the coefficients of directional line in scatter plot. Mixing matrix estimation was accomplished by determining the numbers of local maximum values and calculating their values. In order to eliminate the peak cluster in Hough transform, a method was proposed, i.e. detecting directional density of time-frequency coefficients to determine these outlier points and then removing them, taking Hough transform again to improve Mixing matrix estimation accuracy. The experiment results show this algorithm can accomplish the source numbers estimation under unknown source numbers, and the mixing matrix estimation accuracy is obviously higher than those normal K-means methods. underdetermined blind source separation; mixing matrix estimation; Hough transform; local directional density; outlier time-frequency coefficients 2014-09-22 国家自然科学基金资助项目(51204145,61102110);河北省自然科学基金资助项目(E2013203300,E2016203223);河北省高等学校自然科学研究计划项目(Q2012087);秦皇岛市科学技术研究与发展计划项目(201302A033) 孙洁娣(1975—),女,博士,副教授,E-mail:wjtsjd@163.com. TN 911.7 A 1001-0645(2016)11-1188-06 10.15918/j.tbit1001-0645.2016.11.0172 孤立点检测与霍夫变换结合的混合矩阵估计


3 实验结果及分析

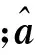
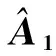
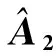


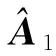


4 结束语
