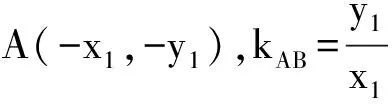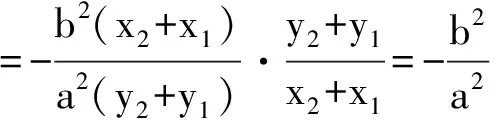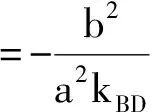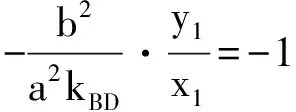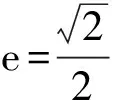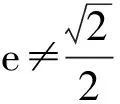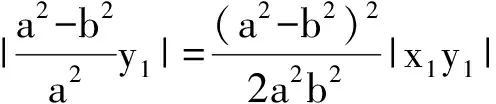两道高考椭圆试题的和谐统一
2016-12-17福建省龙岩第一中学364000
中学数学研究(江西) 2016年12期
福建省龙岩第一中学 (364000)
胡寅年
两道高考椭圆试题的和谐统一
福建省龙岩第一中学 (364000)
胡寅年
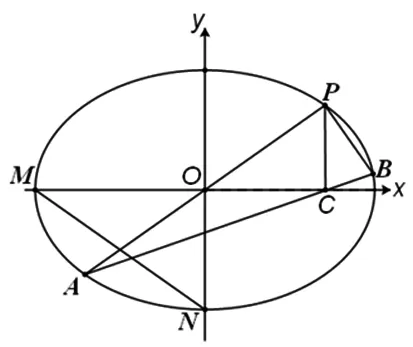
图1
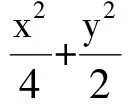
(Ⅰ)当直线PA平分线段MN时,求k的值;
(Ⅱ)当k=2时,求点P到直线AB的距离d;
(Ⅲ)对任意k>0,求证:PA⊥PB.

(Ⅰ)求椭圆C的方程;
(Ⅱ)过原点的直线与椭圆C交于A,B两点(A,B不是椭圆C的顶点).点D在椭圆C上,且AD⊥AB,直线BD与x轴、y轴分别交于M,N两点.
(ⅰ)设直线BD,AM的斜率分别为k1,k2,证明存在常数λ使得k1=λk2,并求出λ的值;
(ⅱ)求ΔOMN面积的最大值.
咋一看,上述两道高考题似乎没有多大的关联性,然而画出题2的图形后,感觉它们的题面惊人的相似,深入探究后我们发现,题2第(Ⅱ)小题的第(ⅰ)问似在题1第(Ⅲ)小题基础上(事隔三年之后)提出的一个崭新问题.
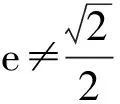
以下,我们将上述两道高考椭圆试题引申为更为一般的情形.
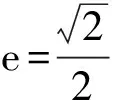
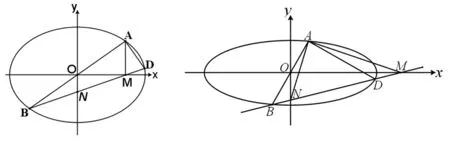
图2 图3