巧用两个原理妙解向量难题

张城兵

(浙江省兰溪市第一中学，321102)



○短文集锦○

巧用两个原理妙解向量难题

张城兵

(浙江省兰溪市第一中学，321102)

向量题中有些涉及分量系数大小和取值范围的问题,若用坐标系来正面对付,会陷入繁杂的计算而一无所获,若另辟蹊径,则是柳暗花明．笔者撷取数例向量难题,介绍两个原理解题的妙用．

一、极端原理

处于“极端位置”或“临界位置”的元素称作“极端元素”,如最大值、最小值、最长、最短等．从极端情形入手,研究极端元素或极端位置,寻找解题的突破口称之为“极端原理”．

故点P形成区域为平行四边形P1P2P4P3.

二、等高线原理

由平面向量基本定理知,x=kλ,y=kμ,所以x+y=k(λ+μ)=k.

(A)1 (B)2 (C)4 (D)8

当P在l2上时,由等高线原理知,x+y=3,故介于l1、l2之间的点P有可能使x+y=2;当P在l3上即与A重合时,x+y=4,但此时不在阴影区域内,故x+y≠4.

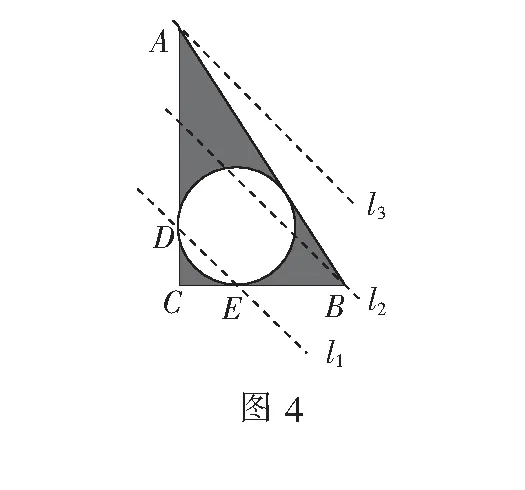
综上,x+y所有可能的整数值为2,选B．

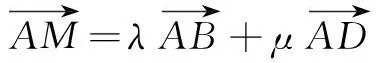
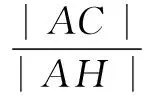
在∆ADH中，