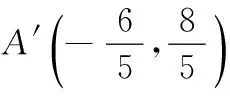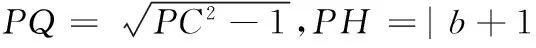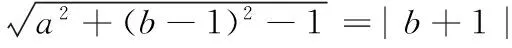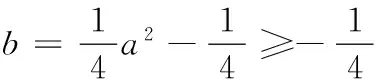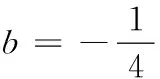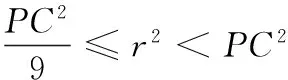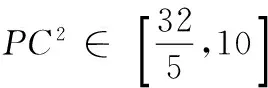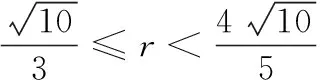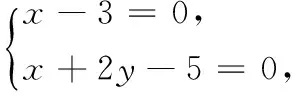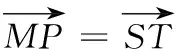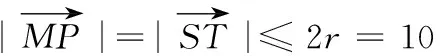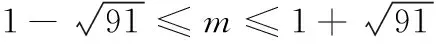高二数学测试



高二数学测试

一、填空题(本大题共14小题，每小题5分，共70分) 1.命题“∃x∈R,x2+1<0”的否定是______.

2.过点(1,2)与直线2x-y-10=0垂直的直线方程为______.

3.已知p:∅⊆{0},q:3≥4,则“p且q”是______命题.(填“真”或“假”)

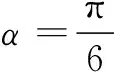
5.若直线ax+2y+3a=0和直线3x+(a-1)y=a-7平行,则a=______.

6.以点(2,-1)为圆心且与直线x+y=6相切的圆的方程为______.

7.巳知椭圆G的中心在坐标原点,焦点在x轴上,过点(0,3)且G上一点到G的两个焦点的距离之和为12,则椭圆G的标准方程为______.

9.过点P(1,2)的直线l与圆O:x2+y2=4相交于两点A,B两点,若∠AOB=120°,则直线l的方程是______.

10.若存在实数x∈[1,2]，满足

则实数a的取值范围是______.

11.圆(x-3)2+(y-3)2=9上到直线3x+4y-11=0的距离等于1的点有______个.

13.已知点P(x,y)满足

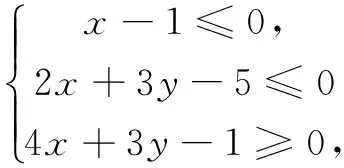
点Q(x,y)在圆(x+2)2+(y+2)2=1上,则|PQ|的最小值为______.

14.在平面直角坐标系xOy中,已知直线y=x+2与x轴,y轴分别交于M,N两点,点P在圆(x-a)2+y2=2上运动,若∠MPN恒为锐角,则实数a的取值范围是______.

二、解答题(本大题共6小题,共90分．解答应写出必要的文字说明、证明过程或演算步骤)

15.(本小题满分14分)设p:|4x-3|≤1,q:(x-t)(x-t-1)≤0,若p是q的充分不必要条件,求实数t的取值范围.

16.(本小题满分14分)已知命题p:方程x2+mx+1=0有两个不相等的负实根,命题q:方程4x2+2(m-2)x+1=0无实根.若p或q为真,p为真,求实数m的取值范围.

17.(本小题满分15分)已知∆ABC顶点A(2,0),AB边上的中线所在直线的方程为19x-y-2=0,∠B的平分线所在的方程为y=2x,

(1)求点B的坐标;

(2)求BC边所在的直线方程.

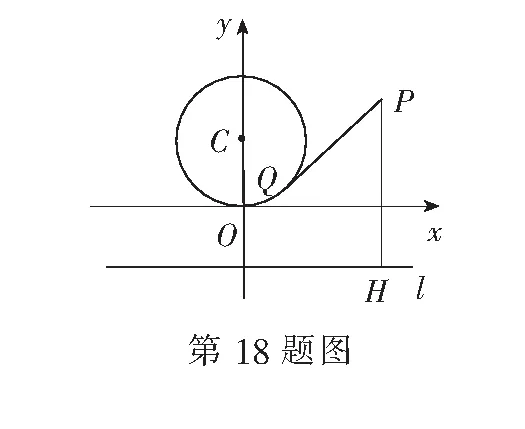
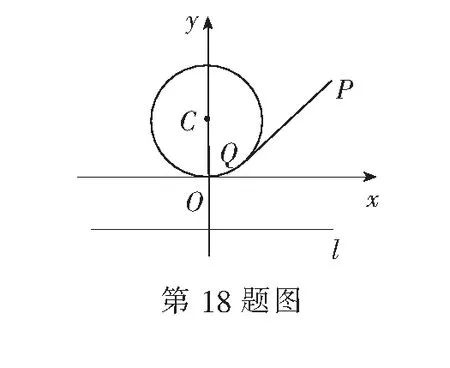
18.(本小题满分15分)已知⊙C:x2+(y-1)2=1和直线l:y=-1,由⊙C外一点P(a,b)向⊙C引切线PQ,切点为Q,且满足PQ等于点P到直线l的距离.

(1)求实数a,b满足的关系式;

(2)设M为⊙C上一点,求线段PM长的最小值;

(3)当点P在x轴上时,在l上求一点R,使得|CR-PR|最大.

19.(本小题满分16分)已知∆ABC的三个顶点A(-1,0),B(1,0),C(3,2),其外接圆为圆H.

(1)求圆H的方程;

(2)若直线l过点C,且被圆H截得的弦长为2,求直线l的方程;

(3)对于线段BH上的任意一点P,若在以点C为圆心的圆上都存在不同的两点M,N,使得M是线段PN的中点,求圆C的半径r的取值范围.

20.(本小题满分16分)已知圆C经过点A(4,0)和直线l:(k-1)x-2y+5-3k=0上定点P,且圆心在直线x-2y+1=0上,

(1)求定点P的坐标;

(2)求圆C的方程;

参考答案

一、填空题

1.∀x∈R,x2+1≥0; 2. x+2y-5=0;

3.假; 4.充分不必要;

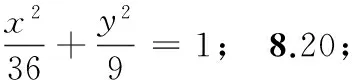
9.x=1或3x-4y+5=0; 10.a<5;

二、解答题

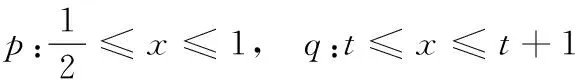
∵p是q的充分不必要条件,

16.由命题p,可以得到

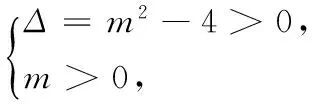
由命题q,可以得到

Δ=[2(m-2)]2-16<0,

∴ 0

∴p为假,q为真,故有

∴x0=-2,∴B(-2,-4).

∴BC边所在的直线方程为7x-y+10=0.

18.(1)过点P作PH⊥l于点H,

则由题意,可得

因为PQ=PH,所以

即 a2+(b-1)2-1=(b+1)2,

整理得a,b满足的关系式是a2=4b+1.

由平面几何可知,当PC最小时线段PC与⊙C交于M,此时PM的值最小.

(3)因为a2=4b+1,令b=0,得a=±1.

由题意知P1(1,0),P2(-1,0).

由平面几何可知,当R为直线CP与直线l的交点时,|CR-PR|取最大值.

因为直线CP1方程为y=-x+1,直线CP2方程为y=x+1,

故当点P的坐标为(1,0)时,点R的坐标为(2,-1);

当点P的坐标为(-1,0)时,点R的坐标为(-2,-1).

19.(1)x2+y2-6y-1=0.

(3)作CQ⊥MN,则Q为MN中点,

∴PQ=3QN.

设CQ=d,则有

PQ2=PC2-d2,QN2=r2-d2,

∴PC2-d2=9(r2-d2),

20.(1)由(k-1)x-2y+5-3k=0,得

k(x-3)-(x+2y-5)=0.

即直线l过定点P(3,1).

(2)设圆C的方程为

x2+y2+Dx+Ey+F=0.

由条件,得

∴圆C的方程为x2+y2-14x-8y+40=0,

即 (x-7)2+(y-4)2=25.

∴32+(m-1)2≤100,