利用奇函数的一组性质求解竞赛试题
2016-12-17梁昌金
梁昌金
(安徽省寿县第一中学,232200)
利用奇函数的一组性质求解竞赛试题
梁昌金
(安徽省寿县第一中学,232200)
函数的奇偶性是竞赛的重点内容之一,考查内容灵活多样,特别是与函数其他性质的综合应用更加突出.这类问题从通性通法的角度来处理,显得较为繁琐,若能灵活利用函数的奇偶性的性质,常能达到化难为易、事半功倍的效果.笔者撷取近年来的数学竞赛试题为例,归纳出奇函数的一组性质及其应用.
性质1 若函数f(x)是奇函数,且g(x)=f(x)+c,则必有g(-x)+g(x)=2c.
简证 由于函数f(x)是奇函数,所以f(-x)=-f(x),所以
g(-x)+g(x)
=f(-x)+c+f(x)+c=2c.
解 可以验证f(-x)+f(x)=0,故函数f(x)为奇函数.所以,函数f(x)在[-3,3]上的最大值和最小值的和为0.
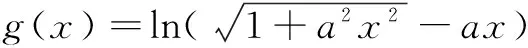
例3 (2013年全国数学联赛贵州省预赛)设函数
的最大值为M,最小值为m,则M+m=______.
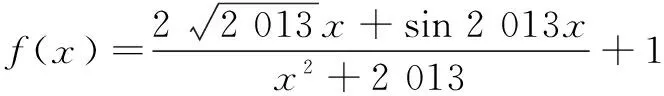
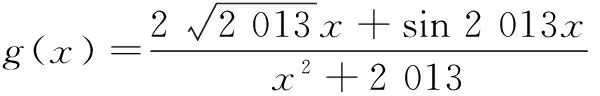
因g(x)max+g(x)min=0,而M=g(x)max+1,N=g(x)min+1,所以M+N=2.
评注 从上述三个例题可知,这类问题的求解关键在于观察函数的结构,构造出一个奇函数.有些问题是直观型的,直接应用即可,但有些问题是复杂型的,需要变形才能成功.
说明 类似地,可以求解如下竞赛试题:
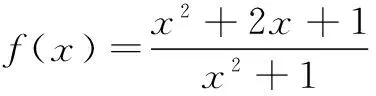
性质2 若f(x)是单调的奇函数,则f(x1)+f(x2)=0⟺x1+x2=0.
略证 f(x1)+f(x2)=0⟺f(x1)=-f(x2)=f(-x2)⟺x1=-x2⟺x1+x2=0.
例4 (2015年全国数学联赛新疆预赛)设x、y是实数,且满足
则x+y=______.
解 设f(x)=x3+2 015x,则f(x)是单调递增的奇函数,且f(x-1)+f(y-1)=0.
所以x-1+y-1=0,故x+y=2.
例5 (2015年全国数学联赛四川省预赛)设x+sin xcos x-1=0,2cos y-2y+π+4=0,则sin(2x-y)=______.
解 由x+sin xcos x-1=0,得2x+sin 2x=2,由2cos y-2y+π+4=0,得
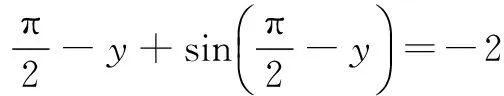
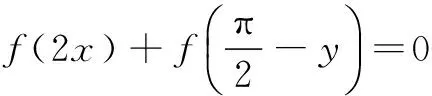
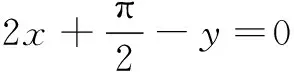
所以sin(2x-y)=-1.
评注 这类问题求解的关键是观察所给函数式,对系数进行合理的变形,使之满足共同的函数特征,然后构造出单调的奇函数.
说明 类似地,可以求解如下竞赛试题:
性质3 已知函数f(x)是区间I上的奇函数.
① 若f(x)在区间I上单调递增,且x1,x2∈I,则f(x1)+f(x2)>0⟺x1+x2>0;
② 若f(x)在区间I上单调递减,且x1,x2∈I,则f(x1)+f(x2)>0⟺x1+x2<0;
③ 若f(x)在区间I上单调递增,且x1,x2∈I,则f(x1)+f(x2)<0⟺x1+x2<0;
④ 若f(x)在区间I上单调递减,且x1,x2∈I,则f(x1)+f(x2)<0⟺x1+x2>0.
略证 ① f(x1)+f(x2)>0⟺f(x1)>-f(x2)=f(-x2)⟺x1>-x2⟺x1+x2>0.
② ③ ④ 类似可证.
解 令g(x)=f(x)-2,则函数g(x)为奇函数且在实数R上为单调递增函数.
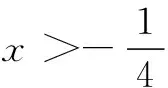
解 原不等式可变形为
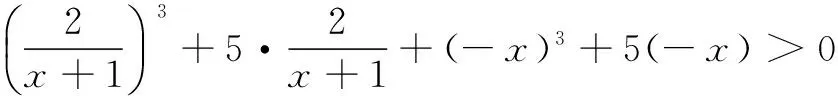
设f(x)=x3+5x,则易知f(x)在R上单调递增,当x≠-1时,原不等式可化为
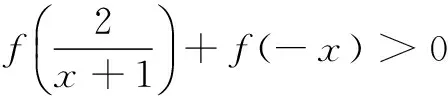
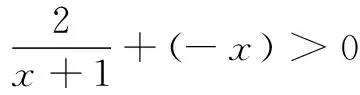
评注 此类问题相对来说较复杂一些,对观察和变形能力要求较高.
性质4 若函数f(x)是奇函数,则函数g(x)=f(x-a)+h的图象关于点(a,h)对称.
略证 函数g(x)=f(x-a)+h的图象可由f(x)的图象平移得到.不难知结论成立.
例8 (2016年全国数学联赛山东省预赛)设α,β分别满足方程α3-3α2+5α-4=0,β3-3β2+5β-2=0,则α+β=______.
解 设g(x)=x3+2x,则g(x)是R上的单调递增的奇函数.
设f(x)=x3-3x2+5x,则f(x)=g(x-1)+3,故f(x)关于点(1,3)中心对称.
观察题目条件α3-3α2+5α-4=0,β3-3β2+5β-2=0,知f(α)=4,f(β)=2,
所以f(α)+f(β)=6,则点(α,4)与点(β,2)关于点(1,3)对称,故α+β=2.
说明:类似地,可以求解如下竞赛试题:
(2008年全国数学联赛湖南省预赛)设函数f(x)=x3+3x2+6x+14,且f(a)=1,f(b)=19,则a+b=( )
(A)2 (B)1 (C)0 (D)-2
答案:D.
评注 此类问题求解的关键是从所给函数式中分离(或变形)出奇函数,进而得出对称中心,然后利用对称性实现问题的求解.
