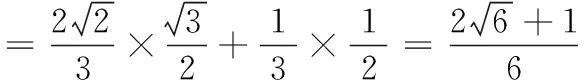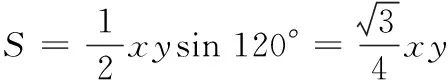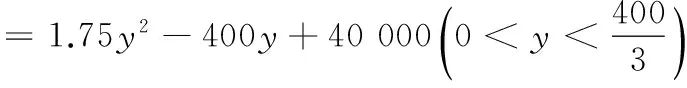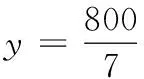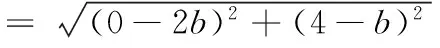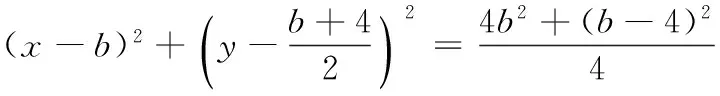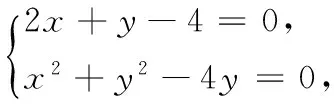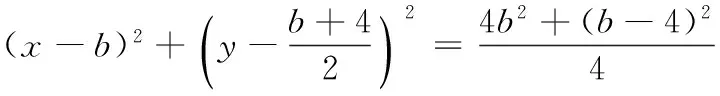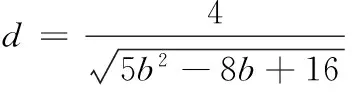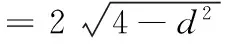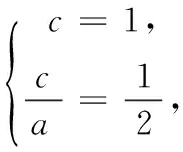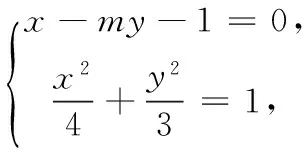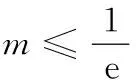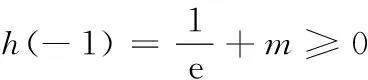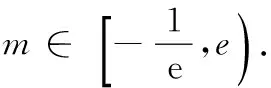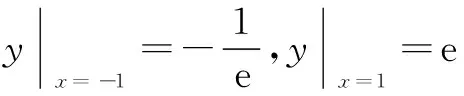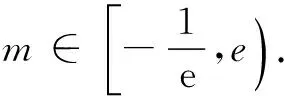高三数学综合测试



高三数学综合测试

一、填空题(本大题共14小题，每小题5分，共70分) 1.设集合A={-1,0,1},B={0,1,2,3},则A∩B=______.

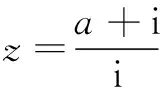
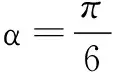
4.过点(1,2)与直线2x-y-10=0垂直的直线(一般式)方程为______.

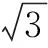
7.若双曲线x2-y2=a2(a>0)的右焦点与抛物线y2=4x的焦点重合,则a=______.

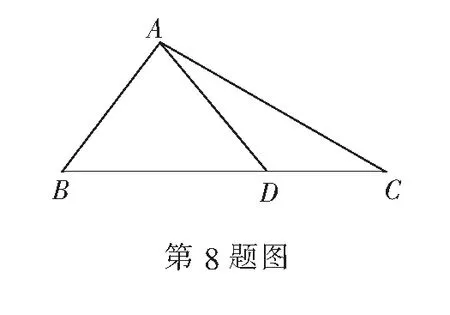
9.设f(x)=4x3+mx2+(m-3)x+n(m, n∈R)是R上的单调增函数,则m的值为______.

10.已知函数f(x)=|2x-2|(x∈(-1,2)),则函数y=f(x-1)的值域为______.

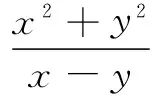
13.已知点A(0,2)是圆M:x2+y2-2ax-2ay=0(a>0)外一点,圆M上存在点T使得∠MAT=45°,则实数a的取值范围是______.

14.已知函数y=f(x)是定义域为R的偶函数,当x≥0时,

二、解答题(本大题共6小题,共计90分. 解答应写出必要的文字说明、证明过程或演算步骤)

15.(本小题满分14分)已知命题p:方程x2+mx+1=0有两个不相等的负实根,命题q:方程4x2+2(m-2)x+1=0无实根.

(1)求B;

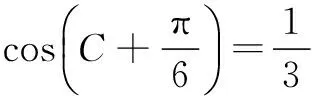
17.(本小题满分15分)如图,某生态园将一三角形地块ABC的一角APQ开辟为水果园种植桃树.已知角A为120°,AB,AC的长度均大于200米,现在边界AP,AQ处建围墙,在PQ处围竹篱笆.

(1)若围墙AP,AQ总长度为200米,如何围可使得三角形地块APQ的面积最大?

(2)已知AP段围墙高1米,AQ段围墙高1.5米,造价均为每平方米100元.若围围墙用了20 000元,问如何围可使竹篱笆用料最省?

18.(本小题满分15分)已知圆M:x2+(y-4)2=4,点P是直线l:x-2y=0上的一动点,过点P作圆M的切线PA、PB,切点为A、B.

(2)若∆PAM的外接圆为圆N,试问:当点P运动时,圆N是否过定点?若过定点,求出所有的定点的坐标;若不过定点,说明理由.

(3)求线段AB长度的最小值.

(1)求椭圆C的标准方程;

20.(本小题满分16分)已知函数f(x)=ex,g(x)=mx+n.

(1)设h(x)=f(x)-g(x).

① 若函数h(x)在x=0处的切线过点(1,0),求m+n的值;

② 当n=0时,若函数h(x)在(-1,+∞)上没有零点,求m的取值范围.

参考答案

一、填空题

1.{0,1}; 2.-1; 3.充分不必要;

4.x+2y-5=0; 5.8;

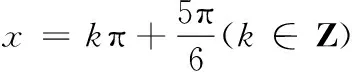
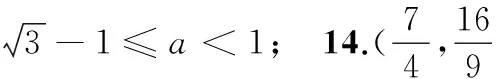
二、解答题

15.由命题p,可以得到

∴ m>2.

由命题q,可以得到

Δ=[2(m-2)]2-16<0,

∴ 0

∴p为假,q为真,

17.设AP=x米，AQ=y米.

(1)x+y=200,∆APQ的面积

当且仅当x=y=100时取等号.

(2)由题意，得

100×(1·x+1.5·y)=20 000,

即 x+1.5y=200.

要使竹篱笆用料最省,只需其长度PQ最短,所以

18.(1)由题可知,圆M的半径r=2,设P(2b,b).

因为PA是圆M的一条切线,所以∠MAP=90°，

(2)设P(2b,b),因为∠MAP=90°,所以经过A、P、M三点的圆N以MP为直径,

其方程为

即 (2x+y-4)b-(x2+y2-4y)=0.

(3)圆N方程为

即 x2+y2-2bx-(b+4)y+4b=0;

①

圆M:x2+(y-4)2=4,

即 x2+y2-8y+12=0.

②

②-①，得圆M方程与圆N相交弦AB所在直线方程为

2bx+(b-4)y+12-4b=0.

点M到直线AB的距离

相交弦长为

19.(1)由题设,得

从而b2=a2-c2=3,

所以,满足题意的定直线l2只能是x=4.

下面证明点P恒在直线x=4上.

设A(x1, y1),B(x2, y2),由于PA垂直于y轴,所以点P的纵坐标为y1,从而只要证明P(4, y1)在直线BD上.

(4+3m2)y2+6my-9=0.

∵Δ=144(1+m2)>0,

①

① 式代入上式,得

kDB-kDP=0,所以kDB=kDP.

∴点P(4, y1)恒在直线BD上,从而直线l1、直线BD与直线l2:x=4三线恒过同一点P,所以存在一条定直线l2:x=4使得点P恒在直线l2上.

20.(1)① 由题意,得

h′(x)=(f(x)-g(x))′

=(ex-mx-n)′

=ex-m,

所以,函数h(x)在x=0处的切线斜率k=1-m.

又h(0)=1-n,所以函数h(x)在x=0处的切线方程为

y-(1-n)=(1-m)x.

将点(1,0)代入,得m+n=2.

② 方法1:当n=0,可得

h′(x)=(ex-mx)′=ex-m,

当x∈(-1,ln m)时,h′(x)<0,h(x)单调递减;当x∈(ln m,+∞)时,h′(x)>0,h(x)单调递增，所以函数h(x)在(-1,+∞)上有最小值为h(ln m)=m-mln m.

令m-mln m>0,解得m

方法2:当n=0,ex=mx.

①x=0时,显然不成立;

(2)由题意,

ex(3x-4)+x+4≥0.

令F(x)=ex(3x-4)+x+4,则

F(0)=0,

且 F′(x)=ex(3x-1)+1,

F′(0)=0.

令G(x)=F′(x),则

G′(x)=ex(3x+2).

因x≥0, 所以G′(x)>0,

所以导数F′(x)在[0,+∞)上单调递增,于是F′(x)≥F′(0)=0,

从而函数F(x)在[0,+∞)上单调递增,即F(x)≥F(0)=0.