基于Matrix Profile的时间序列变长模体挖掘
2021-05-27朱晓晓王继民
朱 旭,朱晓晓,王继民
(河海大学计算机与信息学院,江苏 南京 211100)
0 引 言
作为模式发现和相似性搜索的交叉主题,模体挖掘最先由加利福尼亚大学河滨分校的Lin和Keogh等[1]在2002年首次提出,称这样的模式为“模体”。在相关文献中,模体被定义为重复模式、频繁出现的趋势或近似和重复的序列、形状、片段、子序列等。模体挖掘也可为分类的核心[2]、群集[3-4]、异常检测[5-6]及规则发现[7-8]算法。时间序列模体挖掘技术在遗传学、金融、工业等诸多领域也得到应用。例如,金融领域的证券交易数据[9]、工业领域的用电数据[10]等。
定长模体挖掘仅挖掘由用户指定长度的模体。目前对于定长模体挖掘研究较多。文献[1]提出的Brute-Force算法是第一个模体挖掘算法,算法采取枚举的方式计算所有子序列之间的距离,然后利用最近邻算法找到模体,它具有完全的覆盖率和准确率,被广泛用作基准算法以衡量其他算法的准确性。Chiu等[11]结合SAX算法与概率思想提出了Random Projection算法。Mueen等[12]提出了MK算法,使用早弃技术对Brute-Force算法进行改进,并提出通过选择参考序列得到更紧密的下界距离,从而提高算法效率。Yeh等[13]引入STAMP算法,使用快速相似性搜索算法[14]挖掘时间序列模体。Zhu等[15]对STAMP算法进行改进提出了STOMP算法,其计算速度更快,通过快速傅里叶变换实现子序列间的点积来计算子序列之间的距离,通过重用前一个相邻子序列的点积来加速当前子序列点积的计算。相较于STAMP的随机顺序计算,STOMP是一种有序搜索。
变长模体挖掘无需用户预先指定模体长度,相比时间序列定长模体挖掘更难以解决,针对此问题的研究也相对较少。变长模体挖掘一般以定长模体挖掘为基础,通过在可行长度范围内迭代,得到不同长度的模体。Nunthanid等[16]提出了VLMD算法,利用MK算法计算所有可能长度的模体,然后通过模体分组和提取模体分组代表找到自适应长度的模体。VLMD算法的时间复杂度较高,可扩展性较差。Mueen等[7]提出了MOEN算法,采用下界距离加速Brute-Force算法的效率,以加速枚举不同长度模体。Tang等[17]扩展了K-Motif算法,基于RP算法,定义搜索空间,并使用分段重叠和分段等价类条件从模体分组中获取变长模体。
以上算法虽然在不同方面提高了变长模体的发现速度,但仍然存在参数过多、算法可扩展性差以及时间复杂度高等问题。本文提出一种基于Matrix Profile[15]的时间序列变长模体挖掘算法称为Matrix Profile Variable-Length Motif Discovery (MPVLMD),基于VLMD算法的计算框架,采用STOMP算法挖掘所有可能长度下的定长模体,使用结合增量距离的下界距离技术提升计算速度,引入模体重叠条件、长度相似性条件和模体分组等价类划分,该算法能有效地发现变长模体。基于UCR数据集,针对MPVLMD的运行效率和准确性进行实验,实验结果表明,本文提出的算法具有较高的计算效率和准确性。
1 相关定义
定义1时间序列[18]。时间序列T是在时间上有序的值序列,可记为T={t1,t2,…,tn}。其中,ti表示一个观察值,|T|=n表示时间序列T的长度。
定义2时间序列子序列[19]。时间序列子序列是T中一个更小的时间序列,记为Ti,m={ti,ti+1,…,ti+m-1}。其中,i是子序列在T中的开始位置,m是子序列的长度,并且m>1。
定义3时间序列模体[20]。时间序列模体Mw是指时间序列T中,长度为w且彼此相似度最高的一对子序列。可将其定义为一个四元组:Mw=(d,L1,L2,w),其中,L1和L2为2个子序列的起始位置,满足L1 定义4平凡匹配。给定时间序列T,假设存在子序列C和F,其起始位置分别为p和q。如果p=q,那么C和F属于平凡匹配。 定义5模体重叠[16]。2个长度分别为i和j的模体Mi和Mj,当且仅当它们满足条件:Mi.L1≤Mj.L1 定义6模体分组[16]。模体分组MG是模体的集合,且包含的2个连续模体互相重叠。 定义7模体分组代表[16]。模体分组代表MR,指模体分组MG所包含的所有不同长度的模体中d值最小的模体。 定义8模体分组重叠。2个模体分组MGi和MGj,假设任意Mw∈MGi,Mw∈MGj当且仅当它们满足条件Mw.L1=Mx.L1‖Mw.L1=Mx.L2‖Mw.L2=Mx.L1‖Mw.L1=Mx.L2时,称模体分组MGi和MGj重叠。 定义9变长模体集合。给定时间序列T和模体长度范围[lmin,…,lmax],变长模体集合是所有满足模体长度约束,且彼此不重叠的模体的集合。 定义10距离矩阵。距离矩阵是时间序列中所有的子序列之间欧氏距离的矩阵。距离矩阵的特征表示为: 其中,di,j为时间序列中第i个子序列与第j个子序列之间的欧氏距离。 定义11Matrix Profile[15]。Matrix Profile是时间序列中所有子序列与其最相似的子序列间距离的向量。即距离矩阵中每一列的最小值。向量表示为:(P1,P2,…,Pn-m+1),其中,n表示时间序列长度,m表示子序列长度,Pi表示第i个子序列与所有子序列间距离的最小值Min(Di)。 定义12Matrix Profile Index[15]。Matrix Profile Index是时间序列中所有子序列与其最相似的子序列的索引向量。向量索引表示为:(I1,I2,…,In-m+1),其中Ii表示第i个子序列的最近的邻居。 2016年,Yeh等提出了基于Matrix Profile的时间序列模体挖掘算法STAMP[13],在其基础上,Zhu等进一步提出了STOMP算法[15],在距离矩阵基础上提出了新的数据结构Matrix Profile,该向量中的最小距离值对应的是彼此相似度最高的2个子序列,即为该时间序列的模体。STOMP算法通过快速傅里叶变换计算距离矩阵,从而可以有效地计算给定时间序列的Matrix Profile和Matrix Profile Index[15]。算法包含提取子序列、子序列全连接和模体发现这3个步骤。 根据定义2,使用长度为m的滑动窗口对时间序列T={t1,t2,…,tn}进行分段,截取所有长度为m的子序列,T1,m={t1,t2,…,tm},T2,m={t2,t3,…,tm+1},…,Tn-m+1,m={tn-m+1,tn-m+2,…,tn},获取所有子序列Ti,m={ti,ti+1,…,ti+m-1}(1≤i≤n-m+1)。 子序列全连接用来计算时间序列的距离矩阵。计算所有子序列的均值μ和标准差σ,通过快速傅里叶变换计算子序列Ti,m与所有子序列之间的点积,使用z归一化欧氏距离公式(1)计算2个子序列间的距离。 (1) 其中,m是子序列的长度,μi和μj分别是Ti,m和Tj,m的均值,σi和σj分别是Ti,m和Tj,m的标准差,QTi,j是Ti,m和Tj,m的点积。计算di,j所需的时间只取决于QTi,j计算所需的时间,QTi-1,j-1可以分解为: (2) 并且QTi,j可以分解为: (3) 由式(2)和式(3)可获得式(4): QTi,j=QTi-1,j-1-ti-1tj-1+ti+m-1tj+m-1 (4) 当计算第i个子序列与T中所有子序列的点积时,可以利用第i-1个子序列与T中所有子序列的点积结果加速计算。 求得第i个子序列与T中所有子序列点积之后,使用z归一化欧氏距离计算子序列之间的距离。 根据定义10,使用Matrix Profile存储距离矩阵中每列元素的最小值。同时根据定义11,将最小值的行号作为索引存入Matrix Profile Index。提取Matrix Profile中的最小值对应的索引所指向的子序列是时间序列T的模体。其中,Matrix Profile的结构如图1所示。 图1 Matrix Profile结构图 本文算法基于VLMD算法的计算框架,首先,使用STOMP算法作为子程序,并引入结合增量计算的下界距离加速策略,提升模体提取速度;其次,加入模体重叠和长度相似性条件进行模体分组,踢除过短和存在平凡匹配的模体;再次,加入模体分组重叠条件对模体分组进行等价类划分,剔除提取模体代表时存在的过长模体;最后,提取每个分组等价类中的模体代表,模体代表集合即为变长模体。基于Matrix Profile的时间序列变长模体挖掘算法的流程如图2所示。 图2 MPVLMD算法流程图 STOMP算法只能提取固定长度的模体,本文算法以STOMP作为子程序,在所有可能长度范围内迭代该程序,结合增量计算的下界距离加速策略,加速模体提取。 3.1.1 求解z值数组 依据下界距离的计算流程,首先需要计算对应模体长度的z值。在提取所有可能长度模体的时候,模体长度范围默认为从2~n/2(其中n为时间序列长度),则需要计算长度为n/2-1的z值数组,其具体计算流程如算法1所示。 算法1求解z值数组 forj←m0+1 tomxdo fori←1 ton-jdo Maxj=Y return Max Output:z值数组Max//用于计算下界距离 3.1.2 模体提取 1)提取模长为m0的模体。 使用STOMP算法提取模长为m0的模体,生成按距离升序排列的彼此最相似的子序列对列表List。 2)结合增量计算的下界距离加速策略提取模长为m0+1的模体。 使用缓存技术[21]保存时间序列值的累积和与累积平方和,便于下界距离和增量距离计算。 3)提取所有可能长度的模体。 重复上述步骤,直到获取所有可能长度的模体。 下面阐述下界距离和增量距离的具体求解过程。 通过式(5)求模体长度为m0+1的下界距离: (5) 其中,z=maxi(ti+m0-μi,m0)/σi,m0,(1≤i≤n-m0,当模长为m0时,时间序列中第i+m0个元素归一化后的最大值),d表示模长为m0的子序列间的z归一化欧氏距离集合List中的最大值。 (6) 基于长度为m的tx、ty、(tx)2、(ty)2和txty的运行和,就可以增量计算长度为m+1的距离函数的值。 算法2模体提取 Input:时间序列T,z值数组Max List←STOMP(T,m0)//提取长度为m0的模体,以及n-m0+1对相似子序列集合List z←Maxm0+1 forj←m0+1 tomxdo forp←1 to List.Count do i←List(P).i;k←List(P).k; distance(Ti,j,Tk,j)←List(P).d+ Sum(Ti,j-1,Tk,j-1,(Ti,j-1)2,(Tk,j-1)2,(Ti,j-1,Tk,j-1)); d←distance(Ti,j,Tk,j); NewList.Add (d,i,k)//将距离d,位置i、k存入NewList中 best←NewList.Min z←Maxj L1j←i,L2j←k output List.Min for lengthj else List←STOMP(T,j) Output:模体候选集合List 模体提取阶段产生的模体候选集合List中可能存在较长模体覆盖较短模体的问题,因此对List中的模体进行分组。 遍历List集合中的模体,按照定义5,将满足模体重叠条件的2个模体置入相同模体分组中,反之创建新的模体分组,并将其中未分组的一个模体作为首个元素存储到其中。 遍历所有的模体分组,并对同一个分组中的模体,使用长度相似性条件HMw=⎣n/2w」,修剪过短模体。如果模体Mw的HMw值与其他模体的HMother值不同,剔除模体Mw。其中,n表示时间序列长度,w表示模体长度。 算法3模体分组 Input:模体候选集合List for eachMi∈List do for eachMj∈List,j>i ifMioverlaps withMj Mj.groupid=Mi.groupid for each groupID groupid do Put all motifs that have the groupidiinto groupi for eachMw∈groupido if HMwnot equals to HMother deleteMw return group Output:模体分组集合group 完成模体分组后,模体分组中的模体可能存在以下情况:(si,ti)∈groupi,(sj,tj)∈groupj,并且ti=tj。由于si与ti相似,sj与tj相似,则si与sj有很大概率是相似的。对模体分组集合group进行模体分组重叠判断,遍历group中的每一个模体分组,将满足定义8的模体分组置入同一个模体分组等价类中。 算法4模体分组等价类划分 Input:模体分组集合group for each groupi∈group do for each groupj∈group,j>i if ∀Mx∈groupioverlaps with∀My∈groupj //如果Mx和My满足模体分组重叠条件 groupj.equalclassid=groupi.equalclassid return equalclass Output:模体分组等价类集合equalclass 完成模体分组等价类划分后,每个模体分组等价类将包含平凡匹配的模体。 1)提取等价类模体代表。 每个模体分组等价类中有多个模体分组,每个模体分组中有多个模体。提取模体分组等价类中每个模体分组中z归一化欧氏距离最小的模体,作为每个模体分组的模体代表,每个模体等价类将包含多条模体代表。将这些模体分组的模体代表按照z归一化欧氏距离正序排列,选择中间位置模体代表的z归一化欧氏距离(如果模体分组个数为奇数即为中间位置模体代表的z归一化欧氏距离,如果是偶数取中间2个模体代表的z归一化欧氏距离的均值)作为距离最大值,删除z归一化欧氏距离大于该最大距离的模体代表(修剪具有较大z归一化欧氏距离的过长模体)。 2)输出变长模体。 经过模体分组,模体等价类划分等操作剔除过长、过短和平凡匹配模体后,输出每个模体分组等价类中长度最长的模体代表的集合,所输出的所有不同长度模体代表的集合即为时间序列的变长模体。 算法5变长模体提取 Input:模体分组等价类集合equalclass for each equalclassid∈equalclass do for each groupi∈equalclassid do for eachMw∈groupido//提取每个分组中每个等价类中的模体代表 //按照z归一化欧氏距离正序排列 //提取中间位置的模体作为模体分组等价类的模体代表 return VMotifList Output:变长模体集合VMotifList 以UCR[22]的部分数据集作为实验数据,数据集信息如表1所示。 表1 数据集中所有植入模式的详细信息 UCR数据集是由事先确定好模式长度的已知模式组成,将UCR数据集中已知模式随机植入到随机游走数据中,创建实验所用数据集Dataset。 本文从模体发现的时间效率和准确率这2个方面来分析算法。 实验1验证本文算法的准确性。将本文提出的方法与MN方法[23]以及原始VLMD算法进行比较。采用准确性检测方法AoD[24]作为准确性评价指标,该方法最初用于计算子序列匹配问题中任意子序列对的重叠百分比。本实验用其计算算法输出模体与植入模体间的重叠比,以衡量各算法的准确性。 (7) 其中, max(Lx,Ly)+1 (8) min(LX,Ly)+1 (9) 其中,Lx、Ly为模体开始位置,Sx、Sy为模体长度。 实验2验证不同算法的时间效率。增加算法中待挖掘的时间序列模体长度,对比VLMD的子程序MK算法和MPVLMD的子程序STOMP算法,获取不同长度模体所需的时间。 1)准确性分析。 为了验证MPVLMD算法的准确性,基于2个不同的数据集,分别使用本文算法、MN算法和VLMD算法进行多次模体挖掘实验,统计各算法挖掘模体的结果。并基于本文选用的准确性衡量方法AoD,计算各算法输出模体与预先植入模体的重叠比。所得计算结果如表2所示,具体展示见图3。 表2 各数据集中不同算法发现植入模体的准确率 图3 不同算法发现植入模体的准确率 由图3可知,MPVLMD算法能够发现所有的植入模体,其发现模体的准确率要优于VLMD算法。同时,针对Dataset中的Beef数据,VLMD算法会出现不能发现植入模体的情况,这是因为模体候选集中存在过长、过短和平凡匹配模体影响算法发现模体的整体准确性,这也表明本文算法引入的长度相似性和模体分组等价类条件在筛除无效模体上的积极作用。虽然MN算法也能有效地发现所有的植入模体,但是其发现模体的准确率整体来看要略低于MPVLMD算法,表明本文算法不仅能够有效地发现不同长度的模体,而且具有较高的准确率。 2)时间效率分析。 为了验证MPVLMD算法所选用的模体发现算法STOMP较MK算法的优势,基于Dataset数据集,取算法中待挖掘的时间序列模体长度分别为64、128、256、512、1024进行实验,记录STOMP算法和MK算法获取不同长度模体所需的平均时间,如图4所示。 图4 模体发现耗时 由图4可知,在模体长度相同的情况下,STOMP算法的效率远优于MK算法。并且随着模体长度和数据集长度的增加,MK算法运行所需时间呈现指数增长趋势,其效率快速降低,相反STOMP算法始终能够保持较高的运行速度,其运行时间对模体和数据集长度变化不敏感。 综合上述2个实验的结果可知,MPVLMD算法能够有效地发现时间序列中不同长度的模体,在准确率和时间效率方面均优于原始的VLMD算法。 本文提出了一种基于Matrix Profile的变长时间序列模体挖掘算法MPVLMD,该算法从所有可能长度的模体中自适应返回合适长度的模体。通过模体提取、模体分组、模体分组等价类划分和变长模体提取这4个步骤,将大量可能的滑动窗口长度缩减到真正有意义的几个模体长度,能够有效地发现时间序列中不同长度的模体。 基于UCR数据集的实验结果表明,本文算法具有较高的准确率和时间性能。2 STOMP算法
2.1 提取子序列
2.2 子序列全连接
2.3 模体发现
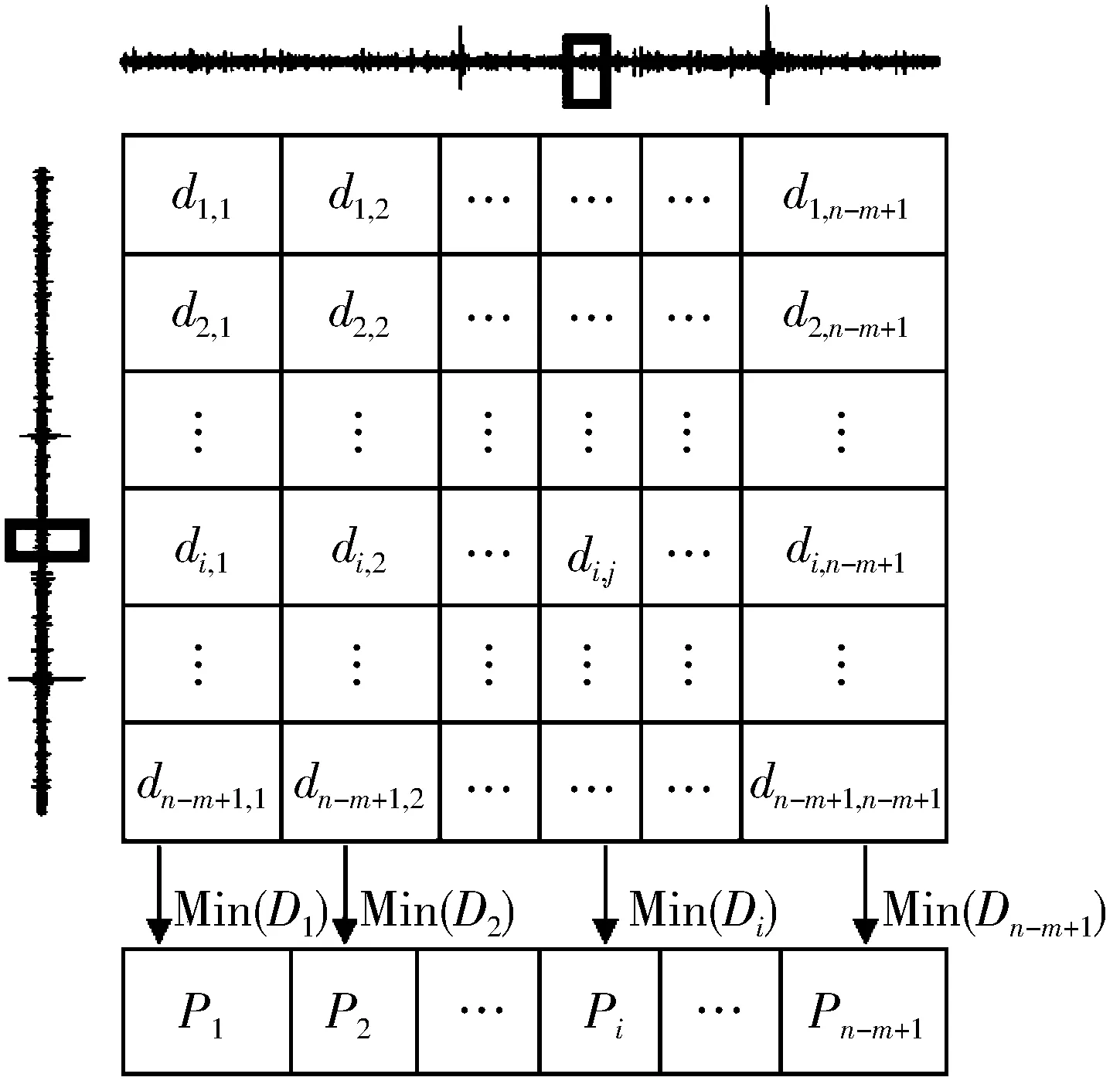
3 基于Matrix Profile的时间序列变长模体挖掘算法MPVLMD

3.1 模体提取

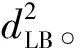



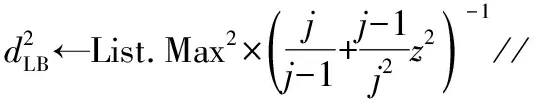
3.2 模体分组
3.3 模体分组等价类划分
3.4 变长模体提取

4 实验与结果分析
4.1 实验数据

4.2 实验方法

4.3 实验结果与分析



5 结束语
