弹道导弹落点精度影响因子分析

施岩龙，马艳琴，马永林

(1. 南京电子技术研究所， 南京 210039； 2. 解放军31001部队， 北京 100091)



·仿真技术·

弹道导弹落点精度影响因子分析

施岩龙1，马艳琴1，马永林2

(1. 南京电子技术研究所， 南京 210039； 2. 解放军31001部队， 北京 100091)

弹道导弹落点预报是预警系统中重要的一个环节，其精确度直接影响预警系统的性能。文中从弹道导弹模型出发，建立了弹道导弹精细化物理模型，从地球椭圆度、大气阻力以及地球自转三方面分析影响弹道目标落点精度的因素，对落点预报估算器进行修正。最后，通过仿真验证了算法的正确性，分析了不同因素对落点精度的影响，并给出了影响中近程弹道导弹落点预报精度的主要影响因素。

落点估算；弹道预报；精度分析

0 引 言

弹道导弹落点预报是预警系统中重要的一个环节。落点预报精确度直接影响预警系统的性能。落点预报一直是国内外研究的热点[1-2]，姚志敏等[3]利用简化数学几何模型进行了发落点预报，试验结果表明落点精度满足要求；高策等[4]基于数值积分法对导弹发落点进行实时预报，实现了对弹体落点的精确预报，满足了靶场测量过程中实时预报的要求；李志鹏等[5]基于改进型反向传播神经网络的弹道落点预测方法，通过样本训练，得到了较高的预报结果;张荣涛、沈慧娜等[6-7]通过雷达数据实时定轨及轨道改进有效提高导弹落点的预报精度；LI X P等[2]，FARINA等[8]利用极大似然法(MLE)、扩展卡尔曼滤波(EKF)以及无味卡尔曼滤波[9](UKF)的方式对落点预报进行比较，采用批处理极大似然法的方式进行落点估算，精度有显著提高。

本文从弹道导弹模型出发，建立了弹道导弹精细化物理模型，分析影响弹道目标落点精度的因素，对落点预报估算器进行修正。最后通过仿真分析验证了算法的正确性。

1 弹道导弹运动模型

弹道导弹在空中飞行包含了三个阶段：发射段(主动段)、自由飞行段(中段)以及再入段。在这三个阶段中，在弹体上作用着不同的力：在发射段有重力、发动机推力、大气阻力；在自由飞行段，受重力及微弱的大气阻力作用；在再入段则受到重力以及大气阻力作用。

本文为了便于描述弹道导弹数学运动模型便于采用地心固定坐标系(ECEF)来描述弹道目标运动轨迹。很显然，由于地球自转的原因，在这里参考坐标系是非惯性的。因此，由地球自转引起的作用在目标上的惯性力(柯氏力和离心力)就必须考虑。在发射段，目标的运动方程描述如下

a=aT+aD+aG+aC

(1)

其中，作用在目标上的加速度分为四部分：发动机推力加速度aT，大气阻力加速度aD，重力加速度aG，以及惯性加速度aC；在被动段，目标的运动方程描述为

a=aD+aG+aC

(2)

发动机推力加速度表示如下

(3)

(4)

大气阻力加速度作用在弹道目标速度的相反方向，其表达式如下

(5)

式中：v(t)为t时刻的速度；h(t)为t时刻目标的海拔高度；m(t)为t时刻目标的质量；S为与速度方向正交的目标的截面积；CD(v)为大气阻力系数；ρ(h(t))表示大气密度函数；

重力加速度作用在弹道目标与地心的连线上，其表达式如下

(6)

式中：P为t时刻目标到地心之间的距离；μG为地心引力常数。

对于惯性加速度aC，它由两项组成：柯氏力产生的加速度以及离心力产生的离心加速度,即柯氏加速度和离心加速度。

主动段运动模型描述如下

(7)

(8)

(9)

(10)

被动段运动模型描述如下

(11)

(12)

(13)

(14)

2 落点精度影响因子

2.1 地球椭圆度修正项

地球位函数只考虑带谐项修正表示如下

(15)

摄动函数为

(16)

通过理论分析重力加速度受地球椭圆度影响只需考虑到J2项即可以满足要求，则

(17)

即

Ce

(18)

2.2 大气阻力影响修正

大气阻力加速度作用在弹道目标速度的相反方向，其表达式如下

(19)

(20)

由于βm(t)/CD(v(t))S可以证明接近于常数，故引入弹道系数变量β，则大气阻力加速度可表示为

(21)

2.3 地球自转影响修正

惯性加速度是由地球自转同时参考坐标系为非惯性系而产生。它由两项组成：柯氏力产生的加速度以及离心力产生的离心加速度

ak：-2ω∧v(t)

(22)

a1：-ω∧(ω∧p(t))

(23)

式中：ak为柯氏加速度；a1为离心加速度；符合∧表示向量之间的外积；ω表示地球自转角速度。

(24)

3 落点估算流程

结合导弹目标飞行的动力学方程，计算各个时间点导弹的位置、速度和加速度。运用龙格库塔法求解动力学微分方程得到任意时间点的位置、速度、加速度以及落点位置。在落点估算过程中，为了减少计算量，采用近地面变步长技术进行处理，即在目标接近地面时，缩小原预测时间步长使发落点预报精度得以提高，还可以根据实际精度要求多次缩小预测时间步长，整个算法流程如图1所示。在落点预报过程中，对落点地区本身的海拔高度也必须考虑，由算法流程可以知道，在每次预测过程中，预测的终止条件为预测位置高度接近地形高度，根据当地地形DEM数据进行匹配发落点地区地形大致高程，如图2所示，从而得到精确的发落点预报值。

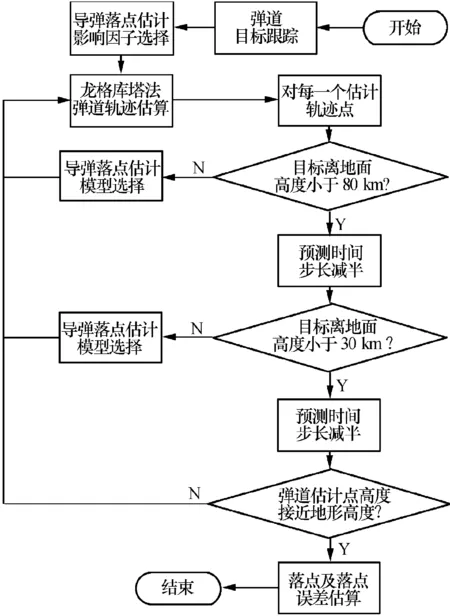
图1 近地变长落点预报算法流程

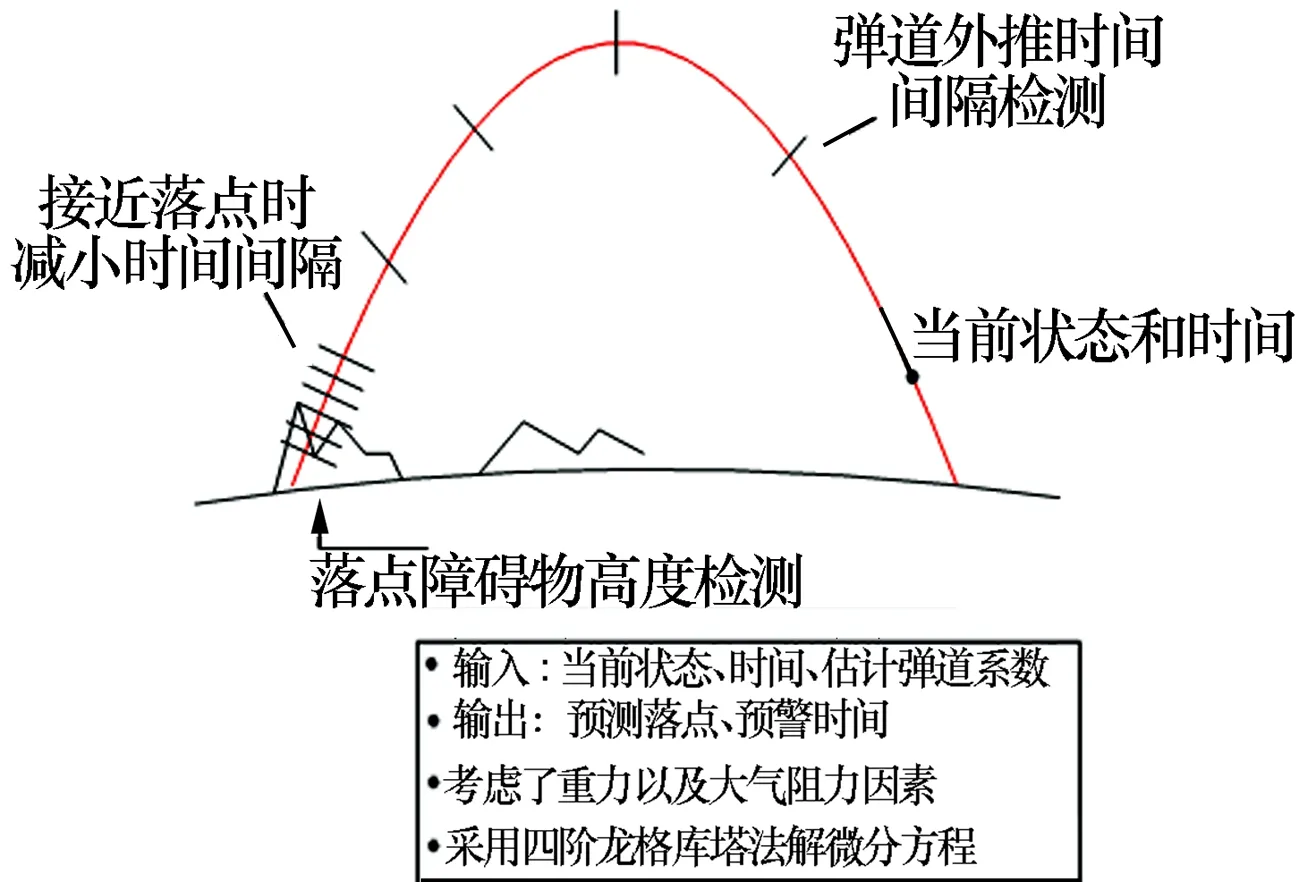
图2 近地变长落点预报

4 数值仿真及结果分析

对弹道目标进行弹道仿真模拟，仿真场景如下：导弹发点为(100.3，42.0，0)，落点为(95.173，39.482，41)，共飞行时间407 s，导弹射程为475 km，射高为157 km，导弹关机时间65 s。给定雷达的部署位置为(99,30,200)，其测距误差为其测距误差为σr=20 m，测角误差为σa=σe=0．01°，跟踪数据率为10 Hz。具体弹道模拟场景，如图3所示。

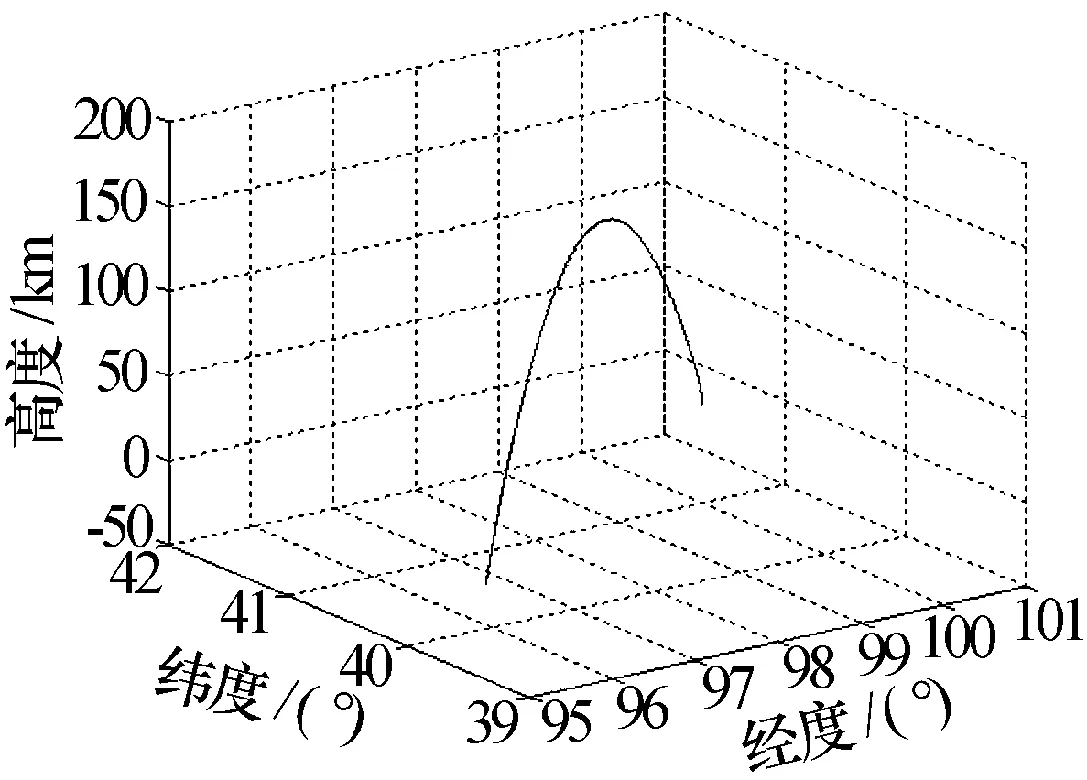
图3 大地测量坐标系下弹道轨迹

通过仿真试验，来验证弹道导弹落点的精度影响因子。图4和图5曲线为弹道预报算法在100次蒙特卡罗仿真条件下，预测轨迹的弹道以及落点的位置。

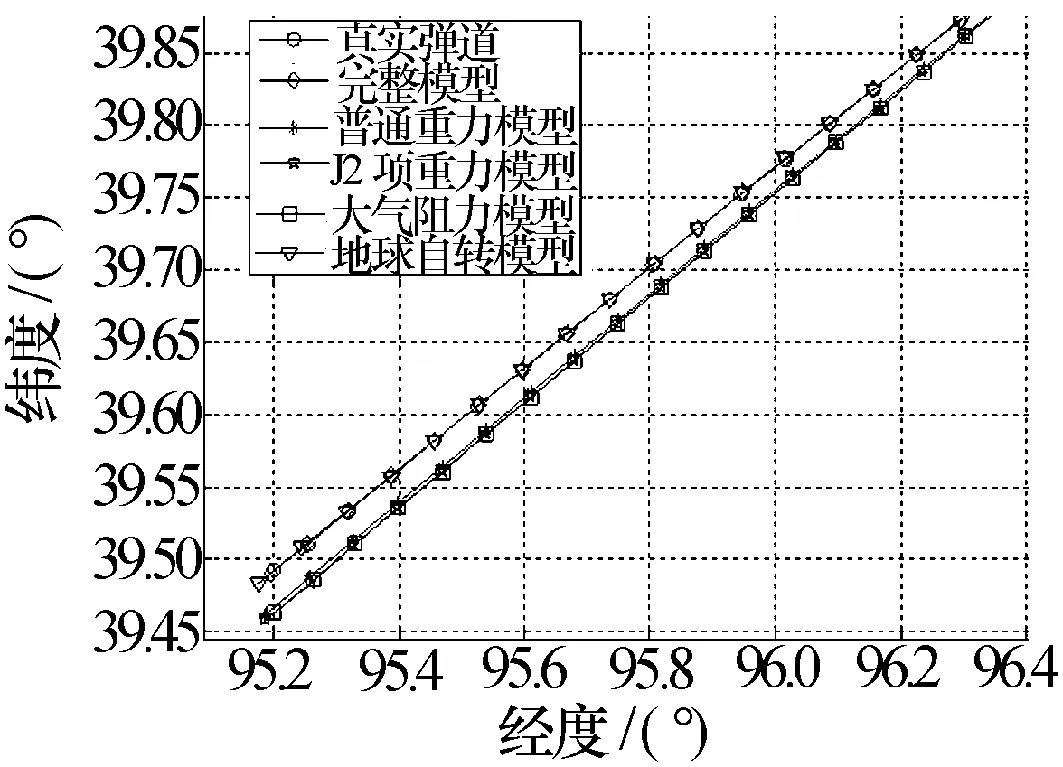
图4 各种修正模型下的预测弹道轨迹

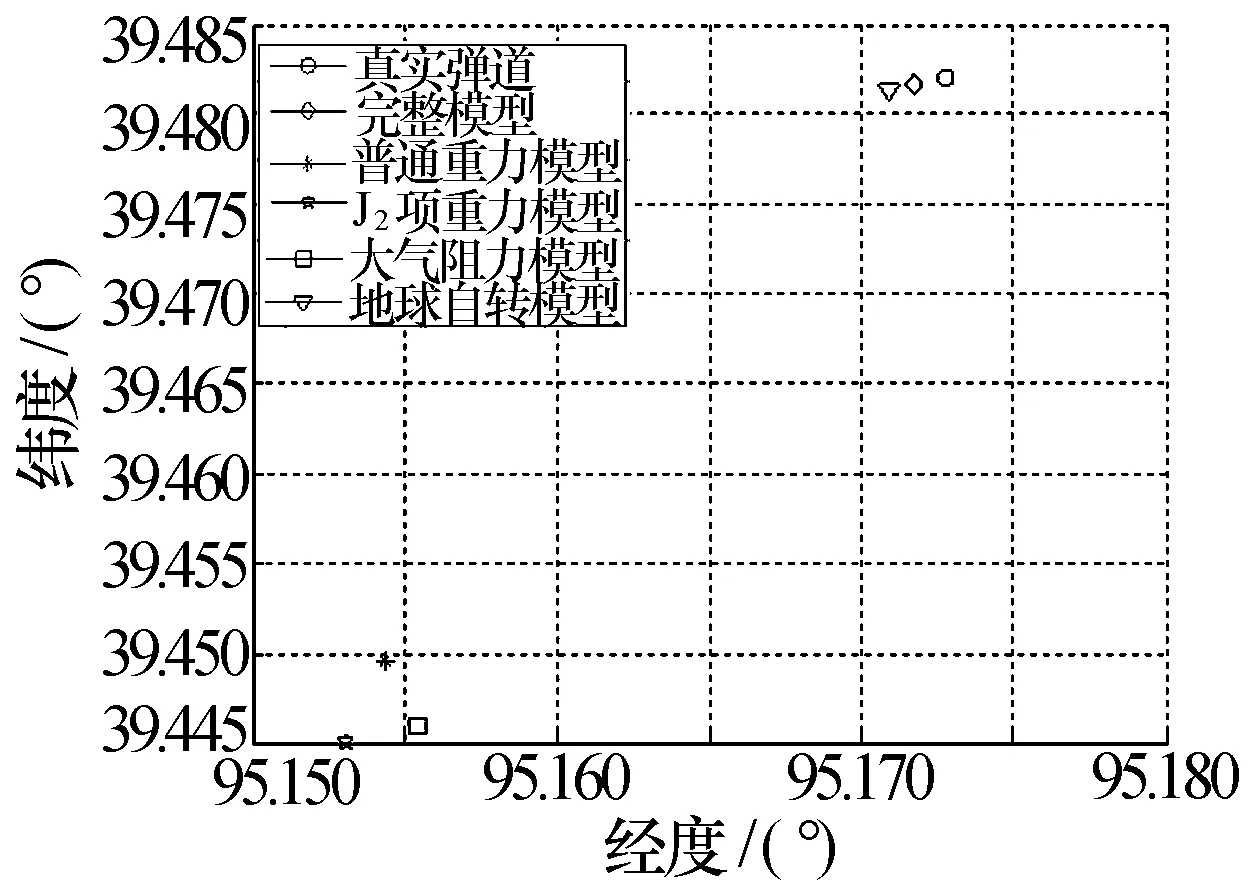
图5 各种修正模型下落点估算

表1为各种修正模型下落点预报的位置以及误差，分析了地球自转、大气阻力、地球非球形引力等因素对落点估算的影响。

试验结果表明：地球自转因素对落点预报影响最大，大气阻力因素次之，普通重力模型与J2项重力模型影响相当，对精度影响最弱。使用J2项重力模型，并考虑地球自转、大气阻力的全模型后，可以得到精确的落点预报。

表1 各种修正模型下落点位置及误差

5 结束语

弹道导弹落点精度受多种因素影响，对落点进行精确的模型误差修正成为提高落点估算精度的关键。本文从弹道目标物理模型进行分析建模，分析了重力模型、大气阻力、地球自转等因素对落点估算精度的影响，从而对落点预报算法进行修正，提高落点精度。但文中只对中近程导弹进行了模拟分析，对于中远程弹道导弹的落点精度影响因子是否有相同结论，还需要进一步研究。

[1] FARINA A, IMMEDIATA S, TIMMONERI L, et al. Comparison of recursive and batch processing for impact point prediction of ballistic targets[C]// 2005 IEEE International Radar Conference. [S.l.]: IEEE Press, 2005: 121-126.

[2] LI X R, JILKOV V P. A survey of maneuvering target tracking-part II: ballistic target models[C]// Proceeding of SPIE Conference on Signal and Data Processing of Small Targets. San Diego: SPIE Press, 2001: 1-23.

[3] 姚志敏，冯振声，马立元. 地地弹道导弹落点计算简化数学模型[R]. GF-A006623G. 石家庄: [s.n.], 2003. YAO Zhimin, FEN Zhensheng, MA Liyuan. Simplified mathematical model for impact point calculation of ground-to-ground ballistic missile[R]. GF-A006623G. Shijiazhuang: [s.n.], 2003.

[4] 高 策，张淑梅, 赵立荣, 等. 基于数值积分法的弹道导弹落点实时预测[J]. 计算机测量与控制, 2012, 20(2): 404-406. GAO Ce, ZHANG Shumei, ZHAO Lirong, et al. A real-time forecast method for impact point of ballistic missile based on numerical methods of integration[J]. Computer Measurement & Control, 2012, 20(2): 404-406.

[5] 李志鹏, 赵捍东, 张 帅, 等. 基于改进型BP神经网络的弹丸落点预测方法[J]. 弹箭与制导学报, 2014, 34(2): 75-77. LI Zhipeng, ZHAO Handong, ZHANG Shuai, et al. A projectile impact-point prediction method based on novel BP neural network[J]. Journal of Projectiles Rockets Missiles and Guidance, 2014, 34(2): 75-77.

[6] 沈慧娜, 徐振来. 提高弹道导弹落点预报精度的动弧平滑平均法[J]. 现代雷达，2009, 31(7): 55-58. SHEN Huina, XU Zhenlai. Moving-arc smoothing averaging algorithm for improving the prediction precision of ballistic missile impact-point[J]. Modern Radar, 2009, 31(7): 55-58.

[7] 张荣涛, 薛金芳, 徐振来. 一种提高导弹落点预报精度方法的研究[J]. 现代雷达，2008, 30(8): 37-39.ZHANG Rongtao, XUE Jinfang, XU Zhenlai. A study on improving missle impact position with orbit improving method[J]. Modern Radar, 2008, 30(8): 37-39.

[8] FARINA A, DELGAUDIO M G, ELIA U D. Detection and tracking of ballistic target[C]// 2004 IEEE Proceedings of the Radar Conference. Rome: IEEE Press, 2004: 450-456.

[9] 王 博，施岩龙．弹道目标被动段跟踪算法研究[J]．中国电子科学研究院学报, 2013, 8(2): 174-177． WANG Bo, SHI Yanlong. Algorithm research of tracking ballistic target at post-boost phase[J]. Journal of CAEIT, 2013, 8(2): 174-177.

施岩龙 男，1979年生，硕士，高级工程师。研究方向为多传感器数据融合、雷达数据处理、弹道目标跟踪与定轨、高性能计算。

Accuracy Analysis of Ballistic Missile Impact Point

SHI Yanlong1，MA Yanqin1，MA Yonglin2

(1. Nanjing Research Institute of Electronics Technology, Nanjing 210039, China)(2. The Unit 31001 of PLA, Beijing 100091, China)

Ballistic missile impact point estimation is a key progress in air defense and anti-missile early warning system(EWS), the capability of EWS is affected by the accuracy of the impact point directly. This paper build a refined physical model of ballistic missile, the factors of ellipticity of earth, drag of atmosphere and rotation of the earth are considered. A comparison of different factors is presented by simulation, the analysis of the main factors affecting of impact point accuracy is described and some conclusions are drawn in the end.

impact point estimate; trajectory predict; accuracy analysis

10.16592/ j.cnki.1004-7859.2016.11.018

施岩龙 Email：sylics@126.com

2016-08-26

2016-10-17

TN958

A

1004-7859(2016)11-0084-04