基于蚁群算法的模糊C均值聚类的改进研究

高晋凯，侯 文，杨冰倩，王贇贇

(中北大学 信息与通信工程学院, 太原 030051)



·信号处理·

基于蚁群算法的模糊C均值聚类的改进研究

高晋凯，侯 文，杨冰倩，王贇贇

(中北大学 信息与通信工程学院, 太原 030051)

在图像分割的研究中，模糊C均值(FCM)聚类算法较之前的硬聚类有了很大的改进，是一种基于函数最优方法的聚类算法，然而传统的FCM算法的聚类中心及个数难以确定，搜索过程易陷入局部最优。因此，提出一种基于蚁群算法的改进的FCM聚类算法。该算法利用了蚁群算法全局优化特征以及较强鲁棒性的特点，将通过蚁群算法得到的聚类中心及个数应用到传统FCM算法中，弥补了传统FCM聚类算法的不足。该算法对图像进行分块处理，并引入多尺度梯度，提高了图像分割的准确性，最后通过实验验证了该算法的有效性及实用性。

图像分割；蚁群算法；模糊C均值聚类；梯度

0 引 言

图像分割是指把一幅图像分成若干互不交叠、有意义的、具有相同性质的区域，并提出感兴趣目标的技术和过程。它是由图像处理到图像分析的关键步骤[1-2]。

模糊C均值(FCM)聚类算法应用于图像分割时，是基于目标函数式的一种局部搜索算法，该算法对初值敏感且容易陷入局部极值，很难得到全局最优解。因此，无法对图像进行准确分割。而且聚类过程中，该算法计算量很大，计算耗时。另外，传统FCM算法仅依据图像的灰度特征来建立目标函数，而图像的特征是多样的。因此，基于灰度特征建立的目标函数式无法完整地描述图像，即难以准确地刻画图像特征。

以往对传统FCM算法的改进，在一定程度上优化了FCM算法，但是仍有存在一定的缺陷。文献[3]中引入了调衡因子，在一定程度上提高了算法的抗噪性，但是需要计算所有样本点间的距离，因此计算量很大，计算所需的时间较长，不利于图像的实时处理；文献[4]提出了更趋明晰的模糊隶属度，该算法虽在一定程度上提高了图像分割的准确性，但其聚类数目人为随机选定，因此其聚类结果具有不确定性；文献[5]中引入了聚类中心引导函数，加快了聚类过程，但是当算法进行到一定程度时，会出现停滞现象，无法找到全局最优解；文献[6]提出的算法适用于灰度有明显变化的图像，不具有普遍性。

本文在文献[7-8]算法的基础上提出了基于蚁群算法的FCM聚类算法的改进，蚁群算法的离散性和并行性特点对数字图像非常适用，基于蚁群算法的全局及分布式优化方法，将蚁群算法与FCM聚类有机结合，可有效提高FCM算法的图像分割效果。该算法在一定程度上提高了图像分割的准确性以及效率，减少了计算量，缩短了计算时间。

1 传统FCM聚类算法的图像分割

1973年，Bezdek[9]提出了FCM聚类算法，作为早期硬C均值聚类(HCM)方法的一种改进。FCM聚类算法通过计算每个样本点对所有类中心的隶属度，并对目标函数不断进行优化找到最优解，从而决定样本点的类属，达到对样本数据集进行聚类的目的[10-11]。

将数据的聚类转化为一个非线性优化问题，并通过迭代来进行求解，是一种非监督模糊聚类标定过程[12-13]。

设图像数据样本集为X={xi|xi=(xi1,xi2, …,xim)}，其中，i=1,2,…,n，n为数据总数，m为每个样本的特征个数，定义隶属度矩阵uij为样本xi属于第j类的隶属度，可表示为

(1)

式中：i=1,2,…,c,j=1,2,…,n，M∈[1+∞)，是一个加权指数；dij=‖xj=ci‖，表示从样本xj到聚类中心ci的欧氏距离。

uij具有如下特征

(2)

聚类中心c={c1,c2,…,cc}，计算公式如下

(3)

目标函数表达形式为

(4)

传统的FCM算法是一个简单迭代的过程，算法步骤为：(1)随机初始化隶属度矩阵，使其满足式(2)特征约束条件；(2)利用式(3)计算聚类中心ci(i=1,2,…,c)；(3)根据式(4)计算目标函数，并判断当目标函数值小于某一阈值,或与上次目标函数值进行比较得出的变化量小于某一阈值，或迭代次数达到最大时，算法停止，否则根据式(1)重新计算隶属度矩阵并返回步骤(2)。

上述算法通过随机初始化隶属度矩阵，并对算法进行简单迭代，多次调整聚类中心及隶属度的值直到目标函数值的变化量达到某一范围，最终确定样本的聚类类别。该算法计算简单，容易实现，但对初值敏感且容易陷入局部极值，很难得到全局最优解，这给图像分割造成十分不利的影响。另外，FCM算法是根据图像的灰度特征来建立目标函数，而图像的灰度是有关图像的“不完全数据”，不能准确地刻画图像特征。因此采用传统的FCM算法无法对图像进行准确分割。

2 基于蚁群算法的FCM聚类算法的改进

改进的FCM首先对蚁群算法中的信息素浓度更新算法进行改进，避免蚂蚁过于集中在某些路径上的信息素浓度增加过快，从而避免蚂蚁算法陷入局部极值，将其应用于FCM聚类算法的搜索过程，则可在一定程度上避免FCM算法陷入局部最优；其次，进行聚类中心的确定，针对图像背景复杂、有噪声等特点引入了多尺度梯度，并将图像进行分块处理来提高图像分割的准确性。

2.1 基本蚁群算法

蚁群算法是一种用来寻找优化路径的几率型算法，由MarcoDorigo[14]于1992年提出，该算法指出在蚁群寻找食物时，它们总能找到一条从食物到巢穴之间的最优路径，并且能够随着环境的变化相应地搜索新的最优路径。

蚂蚁随机地对巢穴到食物源的路径进行选择，当通过某一路径时会留下信息素，信息素以一定速率随着时间挥发，每只蚂蚁在它能感知到的范围内寻找食物，如果有就直接过去。否则就判断是否有信息素，如果判断出周围没有信息素，蚂蚁会根据自己原来的运动方向惯性地运动下去；当周围存在信息素时，蚂蚁能够比较在感知到的范围内哪个方向的信息素浓度高，然后朝着信息素浓度高的方向走。每只蚂蚁都依照该规则朝着信息素浓度最高的方向移动，促使该路径中的信息素浓度不断增强，而强度大的信息素又会吸引更多的蚂蚁，如此便形成一种正反馈机制，正是由于这种正反馈机制，蚂蚁最终发现最短路径[15]。

将蚂蚁寻找食物源的过程看作是一个不断聚类的过程,食物源即是聚类的中心[16]，因此，可以将蚁群算法应用于图像分割，将图像数据集合看作人工蚂蚁，图像分割的过程即为人工蚂蚁寻找食物源的过程。假设图像像素总数为N，将图像的每个像素看作一只蚂蚁，通过提取像素的灰度及梯度特征，可以得到每只蚂蚁的一个表示梯度与灰度的二维向量。

假设图像数据集合为

X={Xi|Xi=(xi1,xi2,…,xim)，i=1,2,…,N}

(5)

式中：m为图像特征，这里取值为2，分别表示梯度与灰度两个特征。

将样本到聚类中心的欧式加权距离表示为

(6)

式中：pk为加权因子,其值可由两个特征对聚类的影响程度而定。

设τij(0)=0为初始信息量，则蚂蚁通过路径(i,j)时留下的信息素浓度可表示为

(7)

式中：r为聚类半径。

根据样本与聚类中心之间的路径上的信息素浓度，Xi归并到cj上的概率Pij(t)为

(8)

式中：ηij(t)=1/dij为启发式引导函数，表征Xi转移到cj的期望程度，即启发式函数越大，像素归于同一类的概率就越大；∂、β分别为聚类过程中信息素及引导函数影响路径选择的因子；K={Xk|dkj≤r,k=1,2,…,j,j+1, …,N}为下一步可选的路径集合。

设置常数P0，当Pij(t)>P0时，将Xi归并到cj类中，设cj={Xs|dsj≤r,s=1,2,…,J}。则可求出更新后的聚类中心为

(9)

式中：Xs∈cj。

蚂蚁在移动的过程中，不同路径上信息素的浓度发生变化，经过一次循环后,依据全局调整规则调整不同路径上的信息素如下

τij(t)=ρτij(t)+Δτij

(10)

式中：ρ为信息素浓度随时间的衰减系数；Δτij为本次循环中路径信息素浓度的增量

(11)

2.2 信息素更新机制的改进

蚂蚁算法通过信息素与引导函数的共同作用进行最大概率的路径选择，当搜索进行到一定程度后，所有蚂蚁个体的解趋于一致。如果该解所对应的路径不是全局最优路径，但其信息素浓度过高时，仅仅依靠公式对路径信息素浓度进行调整会使蚁群算法陷入局部收敛，无法找到全局最优解；当转移概率过大时，虽然有比较快的收敛速度，但会导致算法过早收敛。因此本文提出信息素浓度调节因子ω，调节因子的应用可有效避免蚂蚁过于集中的路径上的信息素浓度增加过快的现象，从而能够避免蚁群算法陷入局部极值。

引入信息素浓度调节因子ω，即

(12)

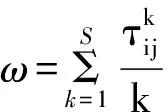
该路径上信息素浓度更新机制表示为

“体”—多面架构成体，实现多层面、多维度的深度协同，具体形式是“教师教育实验区”。以区域教师进修院校为纽带，紧密联系高等院校和中小学教师形成研修联盟，改变教师发展场域，由高校引领理论方向，中小学提供教学实践，实现多层面、多学科、多维度的教学研究，形成群体共振效应，整体提升中小学教师的教学能力。

τij(t)=ρτij(t)-f(ω)

(13)

信息素浓度调节因子ω的引入可在一定程度上避免蚂蚁过于集中于某路径上的信息素浓度增加过快，有利于蚁群算法寻找到全局最优解。将该思想应用到FCM聚类算法中，则可有效避免算法陷入局部最优解，增加了算法的实用性。

2.3 确定聚类中心

大多数处理图像由于背景复杂、有噪声等特点，难以确定合适的聚类中心，而传统FCM算法的聚类结果依赖于初始值的选取。为了提高图像分割的准确性，本文将图像进行分块处理，不同的图像块采用蚁群算法设置不同参数来进行处理。另外，在图像分割过程中，采用一般的图像分割方法提取的目标区域在弱边缘处存在不连续性，图像的边缘是由图像灰度强度的不连续性产生的，这种不连续性可由梯度变化来进行表征。因此，本文中使用多尺度梯度来增大梯度在弱边缘处的响应。

确定聚类中心的过程可分为两步进行：

(1)多尺度梯度值的计算

设图像表示为f(x,y)，由于处理图像是离散的，则图像的梯度可定义为

(14)

上式主要针对图像中变化明显的边缘，如果要用于图像中变化平缓的区域所形成的边缘，则需要扩大特征定义的适用范围,基于此提出了多尺度分析的思想[17],该思想的应用扩大了计算像素梯度时涉及像素的范围,基于多尺度梯度得到的梯度响应能够考虑到距离该像素点较远的像素的差别,提高了平缓区域形成边缘的响应,满足了边缘特征定义广泛适用性的要求。

基于多尺度的梯度可定义为

(15)

式中：l为采样尺度。

(16)

式中：a为待定参数；L为采样的最大尺度。

从该梯度值的计算中，可以看出，随着l增大，距离边缘两侧较远像素的梯度值对边缘的响应影响较小，从而可以在边缘处得到真正的峰值响应。

(2)图像分块处理

将图像分为n×n块进行处理，首先对每个窗口内的各个像素点根据式(16)计算梯度值，将梯度值大于阈值的像素点设为边界或噪声，小于阈值的像素点设为目标或背景，阈值的设定可由各窗口内所有像素点梯度值的均值得到，这样每个窗口内的像素可大致分为两类。

观察各窗口中灰度直方图的峰值点，计算得到各峰值点处的像素点，将得到的峰值像素点设为初始聚类中心，给每个窗口设定蚁群算法参数，即迭代次数、蚂蚁每次迭代的步数及各窗口的信息素矩阵。根据式(8)计算得到蚂蚁移动到该窗口内各聚类中心中的最大概率路径，并沿最大概率路径将像素点归并到该聚类中心，当计算达到迭代次数时，停止计算，可以得到每个窗口内的聚类中心。将得到的聚类中心应用于FCM聚类算法，可以极大地改善FCM算法的局部收敛性，减少FCM算法的计算量。

2.4 改进的FCM聚类算法流程

(1)初始化蚁群算法各参数，如∂、β、Q、M、P0、P1、P2等；

(2)将图像分为n×n个图像块，观察各图像块的直方图，将直方图的峰值点看作初始聚类中心；

(3)由式(16)计算得到各峰值像素点处的多尺度梯度值，当梯度值大于阈值P1时判为边界点或噪声点，当梯度值小于P1时，将像素点判为目标或背景；

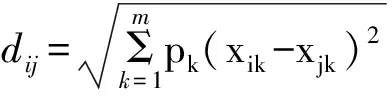
(5)通过式(13)计算各路径上的信息素浓度，并由式(8)计算Xi合并到cj的概率，当概率大于某一值P0时，将Xi合并到cj类中；

(7)当聚类中心变化量小于阈值P2时，停止计算，并输出聚类中心及聚类个数；

(8)将上述计算得到的聚类中心及聚类个数作为改进FCM聚类算法的初始聚类中心及个数，并初始化改进的FCM聚类算法的各参数，如P3、ε等；

(9)由dij=‖xj-ci‖计算欧氏距离dij；

(10)根据式(1)计算隶属度矩阵，根据式(3)更新聚类中心；

(11)由式(4)计算目标函数值，并判断当函数值小于设定阈值P3，或相对于上次目标函数值的变化量小于ε时，或达到最大迭代次数时，停止计算；否则，返回步骤(10)。

3 实验结果及分析

本文在MATLABR2012a环境下，以大小为256×256的三幅图像为例，通过比较传统FCM聚类算法与改进后的FCM聚类算法在图像分割的准确性以及计算时间方面验证算法的有效性及实用性。通过实验，得到每个窗口最佳的迭代次数及步数，取图像分块大小n=5。得到的实验结果如图1所示。

图1 不同分割方法处理图像比较

分析比较以上三幅图像的原始图像及处理后的图像：由图1中的两幅图像，可以看到采用改进FCM算法较传统FCM算法，处理过的青椒图像含杂质点更少，说明改进的FCM算法具有一定的抗噪性；从图2处理图像中的帽檐、嘴唇处可以明显看出改进的FCM算法分割后的图像边界轮廓较明显；图3中经过改进的FCM算法处理过的图像，其远处房子及水面的轮廓也可以比较完整地看到，即图像分割更加准确；加上表1两种算法迭代次数及计算时间的比较，可以得出改进后的FCM算法迭代次数明显减少，缩短了图像处理的时间。

图2 不同分割方法处理图像比较

图3 不同分割方法处理图像比较

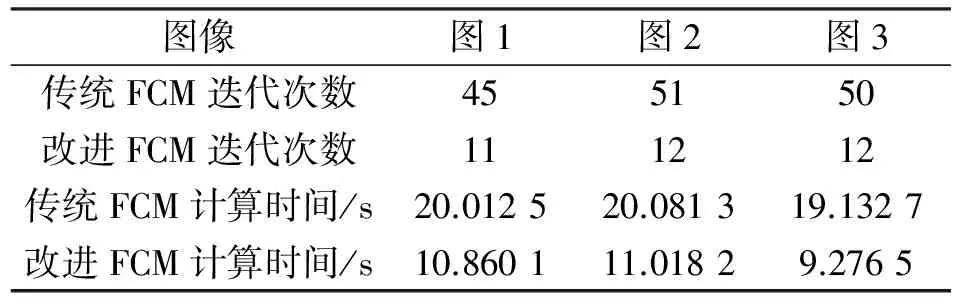
图像图1图2图3传统FCM迭代次数455150改进FCM迭代次数111212传统FCM计算时间/s20．012520．081319．1327改进FCM计算时间/s10．860111．01829．2765

综上可得，基于蚁群算法的改进的FCM聚类算法在图像分割过程中，避免了传统FCM算法易陷入局部最优、抗噪性差及计算量大、计算时间长的缺陷。

4 结束语

本文针对传统FCM算法对初始值敏感，并且容易陷入局部最优，计算时间长等缺点，将蚁群算法与FCM算法有机结合，提出了改进的FCM算法。该改进算法利用蚁群算法来确定初始聚类中心及聚类个数，有效改善了传统FCM算法容易陷入局部最优及计算时间长的缺陷。在图像分割的过程中，采用图像分块处理方法及引入多尺度梯度来提高图像分割的准确性，并在实验中采用不同的图像验证了该算法的有效性。

[1] SHANKAR B U, MEHER S K, GHOSH A. Wavelet-fuzzy hybridization: feature-extraction and land-cover classification of remote sensing images[J]. Applied Soft Computing, 2011, 11( 3): 2999-3011.

[2] 李旭超, 刘海宽, 王 飞, 等. 图像分割中的模糊聚类方法[J]. 中国图像图形学报, 2012,17(4)：447-458. LI Xuchao, LIU Haikuan, WANG Fei, et al. The survey of fuzzy clustering method for image segmentation[J]. Journal of Image and Graphics, 2012, 17(4): 447-458.

[3] 张瑞丽, 张继福. 基于ω-距离均值的模糊聚类算法[J]. 计算机应用, 2012, 32(7)：1978-1982. ZHANG Ruili, ZHANG Jifu. Fuzzy clustering algorithm based on ω-mean distance[J]. Journal of Computer Applications, 2012, 32(7): 1978-1982.

[4] 张 扬, 王士同, 韩 斌. 基于改进模糊聚类算法鲁棒的图像分割[J]. 中国图像图形学报, 2008,13(5)：911-917. ZHANG Yang, WANG Shitong, HAN Bin. Robust image segmentation based on improved fuzzy clustering algorithm[J]. Journal of Image and Graphics, 2008, 13(5): 911-917.

[5] 张 健. 基于蚁群算法的图像分割方法改进研究[J]. 湖州技术学院学报, 2014(1): 84-91. ZHANG Jian. Improvement of image segmentation based on ant colony algorithm[J]. Journal of Huzhou Vocational and Technical College, 2014(1): 84-87.

[6] 薛 琴, 陈 玮, 罗俊奇. 基于梯度算子的蚁群图像分割算法研究[J]. 计算机工程与设计, 2007, 28(23)：5660-5663. XUE Qin, CHEN Wei, LOU Junqi. Research on image segmentation by ant colony algorithm based on gratitude operator[J]. Computer Engineering and Design, 2007, 28(23): 5660-5663.

[7] 陈 亮, 郭 雷. 一种基于蚁群算法的边缘提取算法[J]. 光子学报, 2010, 39(4)：759-763. CHEN Liang, GUO Lei. An edge extraction algorithm based on ant colony algorithm[J]. Acta Photonica Sinica, 2010, 39(4): 759-763.

[8] 余卫宇, 邹若冰, 禹之鼎, 等. 基于局部蚁群算法的图像分割[J]. 计算机应用, 2010, 30(5)：1344-1346. YU Weiyu, ZOU Ruobing, YU Zhiding, et al. Image segmentation based on local ant colony optimization[J]. Journal of Computer Application, 2010, 35(5): 1344-1346.

[9] BEZDEK J C. Pattern recognition with fuzzy objective function algorithm[M]. New York: Plenum Press, 1981.

[10] 康晓东, 何丕廉, 刘玉洁, 等. 基于蚁群算法的医学图像分割研究[J]. 计算机应用研究, 2008, 25(9)：2853-2855. KANG Xiaodong, HE Pilian, LIU Yujie, et al. Study on medical segmentation based on ant colony algorithm[J]. Application Research of Computers, 2008, 25(9): 2853-2855.

[11] 罗 旭, 吴晓军. 蚁群优化算法在WSN路由中的应用研究[J]. 计算及工程与科学, 2015, 37(4)：740-746. LUO Xu, WU Xiaojun. Application study of ant colony optimization in wirelessensor network routing[J]. Computer Engineering & Science, 2015, 37(4): 740-746.

[12] 胡 慧, 何聚厚, 何秀青. 基于模糊理论和蚁群算法的图像边缘连接方法[J]. 计算机工程与应用, 2014, 50(3)：168-172. HU Hui, HE Juhou, HE Xiuqing. Edge linking method based on fuzzy theory and ant colony algorithm[J]. Computer Engineering and Applidations, 2014, 50(3): 168-172.

[13] 白 杨, 孙 跃, 王 君, 等. 基于动态自适应蚁群算法的MRI图像分割[J]. 计算机科学, 2008, 35(2): 226-229. BAI Yang, SUN Yue, WANG Jun, et al. Segmentation of MRI based on dynamic and adaptive ant colony algorithm[J]. Computer Science, 2008, 35(2): 226-229.

[14] 杨立才, 赵丽娜, 吴晓晴. 基于蚁群算法的模糊C均值聚类医学图像分割[J]. 山东大学学报, 2007,37(3)：51-54. YANG Licai, ZHAO Lina, WU Xiaoqing. Medical image segmentation of fuzzy C-means clustering based on the ant colony algorithm[J]. Journal of Shandong University, 2007, 37(3): 51-54.

[15] 屠 莉, 杨立志. 一种基于蚁群优化的图像分类算法[J]. 计算机应用与软件, 2015, 32(4): 202-205. TU Li, YANG Lizhi. An image classification algorithm based on ant colony optimization[J]. Computer Applications and Software, 2015, 32(4): 202-205.

[16] SURI J S, SINGH S, REDEN L. Computer vision and patter recognition techniques for 2-D and 3-D MR cerebral cortical segmention(Part I): a state-of-the-art review[J]Pattern Analysis & Applications, 2002(5): 46-76.[17] FERNANDES C, RAMOS V. ROSA A C. Self-regulated artificial ant colonies on digital image habitats[J].International Journal of Lateral Computing, 2005, 2(1): 1-8.

高晋凯 女，1990年生，硕士研究生。研究方向为智能信息处理。

侯 文 男，1967年生，教授，硕士生导师。研究方向为自动化测试与控制技术、动态测试与智能仪器。

杨冰倩 女，1991年生，硕士研究生。研究方向为图像处理。

王贇贇 女，1990年生，硕士研究生。研究方向为信号处理。

Improved Fuzzy C-means Clustering Based on Ant Colony Algorithm

GAO Jinkai，HOU Wen，YANG Bingqian，WANG Yunyun

(School of Information and Communication Engineering, North University of China, Taiyuan 030051, China)

In the study of image segmentation, fuzzy C-means clustering algorithm (FCM) has been greatly improved compared to the previous hard clustering, which is a clustering algorithm based on a function of best practices. However, the clustering center and number are difficult to be determined for the traditional FCM, also the search process is easy to fall into local optimum. So an improved FCM clustering algorithm is proposed based on the ant colony algorithm.The improved algorithm uses the global optimization features and strong characteristics of robustness of ant colony algorithm.The cluster centers and number obtained by ant colony algorithm are applied to a traditional FCM algorithm to make up for the shortcomings of the traditional FCM. The improved algorithm improves the image segmentation accuracy by processing the image blocks and introducing the multi-scale gradient. Finally the effectiveness and the practicality of the improved algorithm is verified through the experiments.

image segmentation; ant colony algorithm; fuzzy C-means clustering; gradient

10.16592/ j.cnki.1004-7859.2016.11.007

高晋凯 Email：740526799@qq.com

2016-08-17

2016-10-19

TP311.13

A

1004-7859(2016)11-0030-05