基于时间序列模型的雷达数据随机误差建模与补偿

张瑞国，李春雨，丁志宏，许文彤，庞钰宁，叶君好

(中国人民解放军63726部队， 银川 750004)



·数据处理·

基于时间序列模型的雷达数据随机误差建模与补偿

张瑞国，李春雨，丁志宏，许文彤，庞钰宁，叶君好

(中国人民解放军63726部队， 银川 750004)

针对雷达数据随机误差超差的问题，分析了非平稳时间序列自回归求和滑动平均(ARIMA)模型，并以雷达某次实测国际空间站数据的前4 000点数据建立ARIMA模型，设计了基于此模型的Kalman滤波器，利用所设计滤波器对雷达前4 000点数据和剩余数据分别进行了滤波处理，补偿后误差为原数据的13.7%和20.1%。结果表明：该方法能有效降低雷达测量数据随机误差，提高数据质量。

随机误差补偿；非平稳时间序列；卡尔曼滤波

0 引 言

雷达测量数据的随机误差是衡量设备性能的重要指标之一，直接关系到雷达数据的使用质量，如：高精度轨道拟合、不同雷达间数据融合比较、事后目标特征参数提取等[1-2]。在雷达设计时，常采用良好的器件从硬件上降低系统内部噪声，或采用滤波方法从算法上进行数据平滑，使随机误差满足指标要求[3-4]。但由于器件性能下降和使用环境变化等因素，雷达内部噪声起伏较大，加之目标在飞行过程中相对雷达会出现航捷点、姿态翻滚等特殊动作，实时滤波模型很难达到十分精确，导致雷达测量数据的随机误差往往变大甚至超差，严重影响数据质量。雷达研制完成后，其内部硬件和算法一般不再更改，而通过事后数据处理来降低随机差是一种可行有效的手段。

时间序列分析方法是一种描述动态数据统计特性的理论和方法，它可以从有限的样本数据中拟合出具有一定精度的时间序列模型。时间序列模型的突出特点是建模样本数量少，且方便实用，是随机误差建模与补偿的有效手段，在导航、雷达跟踪预报、目标识别等方面得到了广泛应用[5-8]。本文在对雷达测量数据平稳性分析的基础上，建立了雷达数据的自回归和滑动平均(ARIMA)模型，并以所建的ARIMA模型为系统方程，雷达测量数据为量测量，设计了Kalman滤波器。滤波补偿结果表明：本文方法对雷达数据的随机误差具有较好的抑制作用。

1 时间序列模型

时间序列分析法把平稳的有色噪声序列看作由时刻相关的序列和各时刻出现的白噪声组成[9]，即k时刻的有色噪声为

xk= φ1xk-1+φ2xk-2+…+φpxk-p+

ak-θ1ak-1-θ2ak-2-…-θqak-q

(1)

式中：φi<1(i=1,2,…,p)为回归参数；θi<1(i=1,2,3,…,q)为滑动平均参数；ak为白噪声序列。

式(1)即为自回归滑动平均模型ARMA(p,q)，是一种表示有色噪声的递推方程，对于平稳的时间序列，可直接采用ARMA(p,q)进行建模[9]。

在雷达实际测量中，目标通常是运动的，雷达测量数据显然是非平稳的，不能直接采用ARMA进行建模。工程上一般通过多次差分，剔除趋势项，使原序列满足平稳性要求，再采用ARMA建模，之后由ARMA模型反推出原非平稳数据的时间序列模型，即ARIMA建模。

非平稳时间序列的ARIMA模型可表示为[10]

Φ(B)xk=θ(B)ak

(2)

与式(1)相比，式(2)包含d阶差分算子d=(1-B)d，在对非平稳序列建模时，通过将d阶差分算子作用于原非平稳时间序列{xk}，可得到平稳时间序列}。每次对数据序列差分后都要检验新形成序列的平稳性，直到新序列通过平稳性检验，此时得到的差分次数为ARIMA(p,d,q)模型中的差分算子阶数d。

(3)

2 时间序列Kalman滤波器设计

时间序列模型描述了数据序列内在的变化关系，可将所建ARIMA模型看作动态数据输出系统，进而得到Kalman滤波器的系统方程。以雷达实测数据作为外部量测量，得到量测方程。

依据ARIMA(p,d,q)模型中自回归系数的阶数p和差分阶数d可确定系统状态量为Xk=[xk,xk-1,xk-2,…,xk-(p+d-1)]T，系统状态方程表示为

Xk=ΦXk-1+GWk

(4)

系统量测方程表示为

Zk=HXk+Vk

(5)

式中：H为量测矩阵，采用雷达实测数据作为量测值有H=[1 01×(p+d-1)]；Vk为量测噪声，等于雷达测量数据的噪声方差。

3 雷达试验数据建模与补偿

某雷达受测速功能限制，目标测量时只能给出采用距离差分所得的径向速度值，径向速度随机误差通常较大，尤其对于国际空间站等大型空间目标测速数据随机误差严重超差，不利于目标轨迹参数提取、ISAR成像速度补偿等数据分析与处理。通过对雷达测速数据随机差建模与补偿，可有效提高数据质量，有助于目标特征规律建立和完善。

本文以该雷达某次对国际空间站实测的测速数据为对象，对其随机误差进行建模与补偿。测速原始数据如图1所示。

图1 雷达某次对空间站测速原始数据

3.1 试验数据建模

为检验本文方法的有效性，采用图1中前4 000点的数据进行建模，用所建模型对全部测速数据进行滤波处理，检验模型的正确性。

图2 雷达前4 000点测速原始数据

从图2可以看出，雷达测速数据是非平稳的。在进行时间序列分析建模时，先通过多次差分方法将趋势项从非平稳时间序列中直接剔除，并采用逆序检验法对数据进行平稳性检验[9]。在满足平稳性要求后，利用ARMA模型进行建模，之后通过差分算子反求出原始非平稳数据的ARIMA模型，具体建模流程如图3所示。

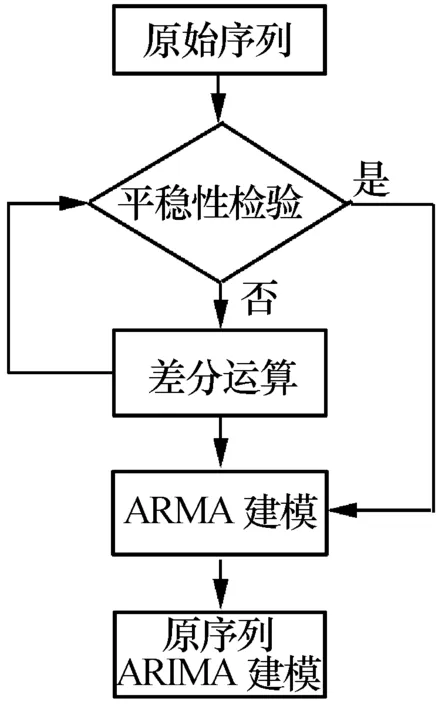
图3 非平稳时间序列建模流程

依据图3的建模流程，对原始测速数据通过两次差分后，逆序法检测平稳性结果为|u|=0.75<1.96，数据达到平稳性要求。测速数据的二阶差分结果如图4所示。

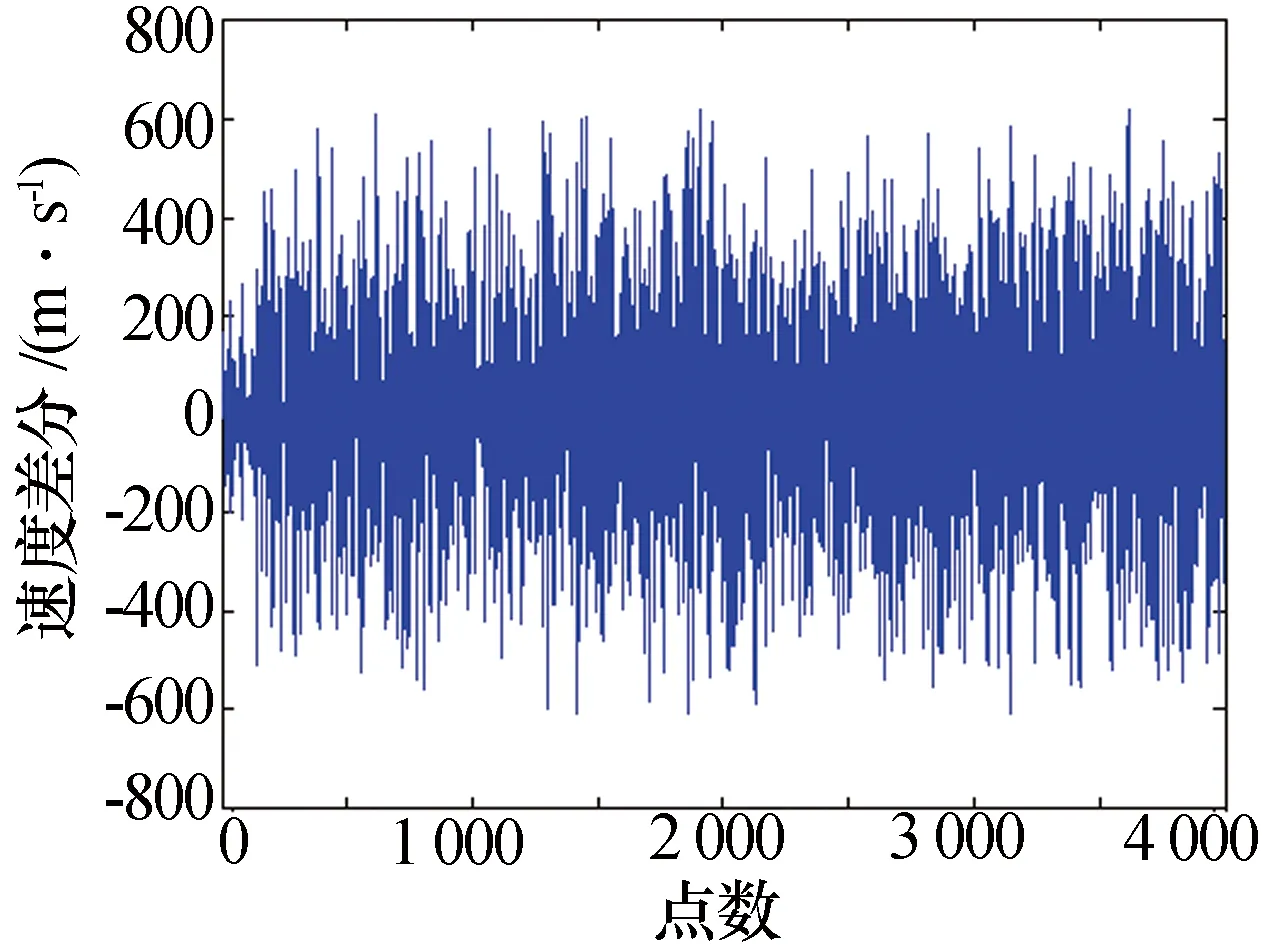
图4 测速数据二阶差分结果

在差分序列达到平稳性要求后，可建立ARMA(p,q)模型，采用相关分析方法，经BIC准则检验[10]，确定AR(3)模型为适用模型，利用Matlab中的AR时间序列函数，得到其模型为

(6)

xk= 2.253 9xk-1-1.939 5xk-2+0.967 8xk-3-

0.132 7xk-4-0.149 5xk-5+ak

(7)

3.2 随机误差补偿

以式(7)所建的时间序列模型作为系统方程，以雷达测量数据作为外部量测量，建立Kalman滤波器。

由式(7)可知，应选取五个连续的随机数据作为Kalman滤波的系统状态变量，即Xk=[xk,xk-1,xk-2,xk-3,xk-4]T，相应式(4)中系统状态转移矩阵为

式(5)中系统量测矩阵为：H=[10000]，Vk为量测噪声，取值为测量数据的均方差。

用建立好的Kalman滤波器对全部雷达测速数据进行滤波处理，得到随机误差补偿前后的径向速度曲线，图5为前4 000点测速数据误差补偿前后结果，图6为剩余数据利用所建模型误差补偿前后结果，为直观显示补偿前后效果，画出了中间某段数据。

图6 剩余测速数据随机误差补偿前后对比

从图5和图6可看出，滤波补偿后雷达测速数据比滤波补偿前要平滑，随机误差得到极大抑制。通过差分方法剔除趋势项[11]，得到补偿前后雷达测速数据的随机误差，求得随机误差均方差如表1所示。

表1 补偿前后测速数据随机误差统计 (m·s-1)

从表1可以看出，前4 000点测速数据经过建模补偿后，随机误差仅为原来的13.7%；剩余数据通过前4 000点数据所建模型进行滤波补偿后，误差也得到较大抑制，为补偿前的20.1%。数据处理结果表明，本文通过1～4 000点有限样本所设计的AR(3)模型能准确反映雷达径向速度数据的变化规律，基于此模型的Kalman滤波器能有效抑制测速随机误差，提高雷达数据质量。本文方法相比于传统分段最小二乘多项式拟合具有建模样本少、受奇异值影响小等优点，是一种有效的雷达数据事后处理方法。

4 结束语

本文对非平稳时间序列建模进行了分析，并以雷达实测数据的前4 000点有限样本建立ARIMA时间序列模型，设计了基于此模型的卡尔曼滤波器。利用所设计的滤波器对雷达前4 000点数据和剩余数据分别进行了随机误差滤波处理，补偿后误差分别为原数据的13.7%和20.1%。数据处理结果表明：本文通过有限样本所建立的时间序列模型能较好地反映雷达数据的变化规律，有效抑制随机误差，解决雷达数据超差问题。本文方法具有工程实用意义，对雷达事后数据分析与处理具有较大应用价值。

[1] 姜大治, 王不了, 杨 军. 多雷达含缺损信息外弹道解算方法研究[J]. 弹道学报, 2015, 27 (1): 44-47. JIANG Dazhi, WANG Buliao, YANG Jun. Research on algorithm for multi-radar trajectories with defect information[J]. Journal of Ballistics, 2015, 27 (1): 44-47.

[2] 王 成, 胡卫东, 郁文贤. 基于非平稳时间序列的雷达信号融合[J]. 信号处理, 2005, 21 (4): 338-343. WANG Cheng, HU Weidong, YU Wenxian. Radar signal fusion based on non-stationary time series processes[J]. Signal Processing, 2005, 21 (4): 338-343.

[3] 魏崇奎, 甘友谊, 叶正茂. 外测数据处理中噪声分离模型的方法研究[J]. 现代雷达, 2007, 29 (8): 79-81. WEI Chongkui, GAN Youyi, YE Zhengmao. A study on method of noise departure model on data processing of trajectory measurement[J]. Modern Radar, 2007, 29 (8): 79-81.

[4] 孙国政, 王索建, 董 扬. 基于ADS-B数据的雷达精度测量方法[J]. 现代雷达, 2011, 33 (2): 18-21. SUN Guozheng, WANG Suojian, DONG Yang. Measurement method for radar precision based on ADS-B data[J]. Modern Radar, 2011, 33 (2): 18-21.

[5] DANG S W, TIAN W F, QIAN F. EMD-and LWT-based stochastic noise eliminating method for fiber optic gyro[J]. Measurement, 2011, 44: 2190-2193.

[6] 江 桥, 王学伟. 机载火控系统动态精度试验数据处理方法研究[J]. 舰船电子对抗, 2005, 28(3) : 50-53. JIANG Qiao, WANG Xuewei. Research on data processing method of airborne fire control system dynamic precision test[J]. Shipboard Electronic Countermeasure, 2005, 28(3): 50-53.

[7] 饶 彬, 屈龙海, 肖顺平, 等. 基于时间序列的弹道目标进动周期提取[J]. 电波科学学报, 2011,26 (2): 291-296. RAO Bin, QU Longhai, XIAO Shunping, et al. Precession period extraction of ballistic targets based on time series analysis[J]. Chinese Journal of Radio Science, 2011, 26 (2): 291-296.

[8] 朱 丽, 龙 兵, 刘 震. 基于ARMA的雷达发射机故障预测及其实现[J]. 计算机测量与控制, 2010, 18(11): 2460-2461. ZHU Li, LONG Bin, LIU Zhen. ARMA-based fault prediction for radar transmitter and its realization method[J]. Computer Measurement & Control, 2010, 18(11): 2460-2461.

[9] 徐 帆, 马广富. 基于ARIMA模型的光纤陀螺随机漂移滤波方法研究[J]. 传感器与微系统, 2007, 26(2) : 31-32. XU Fan, MA Guangfu. Investigation on filter method of FOG drift data based on ARIMA model[J]. Transducer and Microsystem Technologies, 2007, 26(2): 31-32.

[10] 张延顺, 房建成. 小型动调陀螺随机误差建模与滤波方法研究[J]. 仪器仪表学报, 2007, 28(7) : 1286-1289. ZHANG Yanshun, FANG Jiancheng. Research on random error modeling and filtering method for dynamically tuned gyroscope[J]. Chinese Journal of Scientific Instrument, 2007, 28(7): 1286-1289.

[11] 吕韶昱, 郁春来, 万伟建. 相控阵雷达外弹道测量事后数据处理软件设计[J]. 计算机测量与控制, 2007, 15(3) : 399-401. LÜ Shaoyu, YU Chunlai, WAN Weijian. Design of OLDPS of phased array radar in trajectory measurement[J]. Computer Measurement & Control, 2007, 15(3): 399-401.

张瑞国 男，1962年生，高级工程师。研究方向为相控阵雷达总体与目标识别。

李春雨 男，1987年生，工程师。研究方向为雷达数据处理与目标识别。

丁志宏 男，1972年生，高级工程师。研究方向为航天测控与系统总体。

许文彤 男，1970年生，高级工程师。研究方向为航天测控与系统总体。

庞钰宁 男，1980年生，工程师。研究方向为测控系统总体。

叶君好 男，1985年生，工程师。研究方向为临近空间大气建模。

Modeling and Compensation of Radar Data Random Error Based on the Time-series Model

ZHANG Ruiguo，LI Chunyu，DING Zhihong，XU Wentong，PANG Yuning，YE Junhao

(The Unit 63726 of PLA, Yinchuan 750004, China)

Aiming at the problem of considerable radar data random error, the autoregressive integrated moving average (ARIMA) model is analyzed by time-series analysis method. The ARIMA model and Kalman filter are designed based on the foregoing 4 000 data points to smooth the radar data, which is obtained by measuring the International Space Station. The foregoing 4 000 data points and other points are processed by the filter respectively, and random error reduces to 13.7% and 20.1% of the original data separately. The results show that the random error of radar measurements can be reduced effectively by the new method, improving the data quality.

random error compensation; nonstationary time series; Kalman filtering

10.16592/ j.cnki.1004-7859.2016.11.011

李春雨 Email：spring0464@126.com

2016-08-23

2016-10-17

TP971.1

A

1004-7859(2016)11-0049-04