ECEF坐标系弹道导弹跟踪研究

许登荣，程水英，包守亮

(电子工程学院 504教研室, 合肥 230037)



·数据处理·

ECEF坐标系弹道导弹跟踪研究

许登荣，程水英，包守亮

(电子工程学院 504教研室, 合肥 230037)

针对单模型跟踪算法无法实现对弹道导弹连续精确跟踪的问题，提出了一种地心地固坐标系下弹道导弹全阶段连续跟踪的交互式多模型(IMM)算法。根据导弹不同飞行阶段的受力情况建立IMM算法的两个滤波模型集：助推段采用恒轴向力模型，中段、再入段采用被动段跟踪模型，两个模型都利用滤波精度高、数值稳定性较好的求容积卡尔曼滤波算法进行滤波。针对该IMM算法在混合估计过程中引入偏差的问题，采用无偏混合的方法，以两种典型的跟踪场景进行仿真校验，实验结果验证了该文算法的优越性。

机动目标跟踪；弹道导弹；交互式多模型算法；求容积卡尔曼滤波

0 引 言

弹道导弹自问世以来，因其具有射程远、速度快、突防能力强、打击精度高、杀伤威力大、效费比高等优点受到全世界的关注，针对它的防御研究也从未停止过。弹道导弹跟踪是弹道导弹防御的核心问题之一，跟踪的精度决定了落点预测的精度以及导弹拦截的成功率。弹道导弹的飞行阶段通常可以分为主动段和被动段，其中，主动段又叫作助推段，被动段又可分为中段和再入段。大多数有关导弹跟踪的文献通常只对导弹某一飞行阶段进行研究[1]，但采用这种普通方法不能实现导弹的连续精确跟踪。近些年来，一些文献提出利用交互式多模型算法对弹道导弹进行连续跟踪[2-4]，减小了导弹不同飞行阶段过渡处的跟踪误差，提高了导弹的跟踪精度。但多模型算法性能的好坏很大程度上取决于所选的模型集[5]，针对大多数导弹跟踪文献中建立的模型较为粗糙的问题，本文根据导弹不同飞行阶段的受力情况建立交互式多模型(IMM)算法较为精确的滤波模型集，实现对弹道导弹全阶段的连续高精度跟踪。

此外，弹道导弹跟踪存在一个坐标系选择的问题。合理而恰当地选择参考坐标系会使描述导弹运动规律的数学模型大为简化，否则会导致问题复杂化，甚至陷入无法处理的困境[6]。目标运动的描述通常在笛卡尔坐标系中，但量测值却在传感器坐标系中描述。因而，对于导弹跟踪来说，坐标系的选择存在四种可能性[7]，即混合坐标系、笛卡尔坐标系、传感器坐标系，以及其他坐标系。文献[7-8]对不同坐标系中跟踪的优缺点进行了分析。目前大部分的导弹跟踪算法都选择在混合坐标系中进行处理[8]，即在东-北-天(ENU)坐标系中建立目标的状态方程，量测值在雷达球坐标系中进行描述。但是在ENU坐标系中描述导弹运动的数学模型较为复杂，而在地心地固(ECEF)坐标系中不仅对导弹目标进行受力分析非常的方便，而且ECEF坐标系中目标的状态方程也十分简洁。此外，全局的战场态势演示等在ECEF坐标系中更为形象和直观。鉴于此，本文选择在ECEF坐标系中对导弹目标进行跟踪。

本文采用IMM算法实现无先验信息条件下对弹道导弹全阶段的连续跟踪，在对导弹各阶段受力分析的基础上，在ECEF坐标系中建立了IMM算法的两个滤波器模型。主推段目标的轴向力近似保持不变[1，4]，采用恒轴向力(CAF)[1-2]模型；中段和再入段采用将弹道系数扩展为目标状态分量进行联合估计的被动段跟踪模型，记为PM模型。反导雷达的量测在雷达站球坐标系获得，因而需要将量测转换到ECEF坐标系中。这个过程分为两步：先将雷达球坐标系量测转换到ENU直角坐标系中，再转换到ECEF坐标系中。但若球坐标系转换到直角坐标系是有偏的，会造成滤波器的性能下降。针对此问题，本文先采用修正的无偏量测转换(MUCM)方法[9-10]将雷达量测转换为ENU坐标系伪线性量测，再将ENU坐标系量测和相应的协方差转换到ECEF中，并给出了转换过程的推导，从而建立了对导弹全阶段连续跟踪所需的状态方程和量测方程。由于状态方程非线性，本文在滤波实现上采用数值精度较高、稳定性较好的求容积卡尔曼滤波(CKF)算法[11]，同时比较了几种主流的非线性滤波算法在弹道目标跟踪的性能。另外，由于该IMM算法的两个滤波模型状态维数不同，而要现实混合交互，需要将各模型的状态向量转化一致[12]，但在混合的过程中引入了偏差，针对这个问题，采用无偏混合[13]的方法。仿真结果表明：该算法能实现对弹道导弹连续精确跟踪，且不同飞行阶段过渡处的跟踪误差较小。

1 弹道导弹跟踪模型

1.1 运动模型

由于弹道导弹受力复杂且不同阶段的受力不一样，很难用统一的数学模型进行描述，本文在受力分析的基础上分别建立了弹道导弹不同阶段的跟踪滤波模型。

1.1.1 主动段跟踪模型

ECEF坐标系中，弹道导弹在主动段受到的作用力主要有推进力、空气阻力、地心引力和外在力(包括离心力和柯氏力)。由于推进力和空气阻力的一些参数与目标具体型号有关，在无先验的情况下难以建立弹道导弹准确的运动模型。但推进力和空气阻力与目标的速度几乎在同一条直线上，这样除重力以外的其他力可以合成一个轴向力，且基本保持不变。设ECEF坐标系中目标的状态向量为xCAF=[xyzxyzab]T，位置矢量和速度矢量分别为p=[xyz]T，v=[vxvyvz]T。地球模型为椭球模型(WGS-84)，则助推段可以采用如下CAF模型对目标进行跟踪

(1)

1.1.2 被动段跟踪模型

被动段包括中段和再入段，和主动段相比，被动段不受推进力的作用，即受到的作用力主要是地心引力、空气阻力和外在力。其中，中段目标受到的空气阻力通常可以忽略，仅考虑重力和外在力的影响。而目标重返大气进入再入段时，受到的作用力主要是地心引力和空气动力，可以忽略外在力的影响，但由于空气阻力与弹道系数有关且未知，需要对弹道系数进行估计。因此，大多数有关文献中段采用六状态的跟踪模型，再入段采用将弹道系数扩展为目标状态的一个分量进行实时估计的七状态模型对目标进行跟踪。为了实现对弹道目标更加精确的跟踪，本文中段和再入段考虑所有作用力的影响，同时为了减小IMM算法模型的数量，降低计算量，中段和再入段都采用如下七状态的被动段模型对目标进行跟踪。即设目标的状态变量为xPM=[xyzxyzα]T，则ECEF坐标系中被动段弹道导弹的运动方程为[1]

(2)

式中：ρ(h)=ρ0e-k0h为空气密度，其中，h为目标离地面的高度，ρ0=1.22 kg/m3，k0=1.414 1×10-4m-1；α=1/β为空气阻力参数，β为弹道系数；wα(t)为零均值的高斯白噪声。

到此，建立了弹道导弹各阶段的运动方程，可以看到，上述方程都是用微分方程进行描述的，且都是非线性的。而为了利用相关的非线性滤波技术进行递推估计，通常需要将微分方程离散化，状态方程离散化的方法有欧拉逼近法[14]、一阶泰勒级数展开法[13]和四阶龙格库塔积分法[1,4]等。本文利用的是一阶泰勒级数展开法。

1.2 量测方程

反导雷达的量测在球坐标中获得，量测值的表达式为

(3)

式中：xENU,k、yENU,k、zENU,k为k时刻目标在雷达ENU坐标系下的位置坐标；zSPH, k=[Rm,Am,Em]T为雷达的观测值，其中，Rm为目标到雷达的距离，Am为方位角，Em为俯仰角；vSPH,k为零均值的高斯白噪声序列，其协方差矩阵为RSPH,k。要实现递推滤波估计，必须建立量测值与状态变量之间的关系。本文先采用MUCM方法将球坐标量测转换为ENU坐标系线性量测，然后将ENU坐标系量测和相应的协方差转换到ECEF中，从而建立了滤波所需要的量测方程。设经过MUCM方法转换后的量测向量及协方差矩阵分别为zENU，k=[xMUCM,kyMUCM,kzMUCM,k]T，RENU,k=E((zENU,k-E(zENU,k))(zENU,k-E(zENU,k))T)，其转换详细过程可参考文献[8]。

假设雷达站所在大地经度为L，大地纬度为B，高程为H，地球为椭球模型，则雷达站中心位置Or在ECEF坐标系下的坐标为

(4)

(5)

(6)

设由ENU坐标系转换到ECEF坐标系的量测及协方差矩阵分别为zECEF,k，RECEF,k，则

(7)

RECEF,k= E((zECEF,k-E(zECEF,k))(zECEF,k-E(zECEF,k))T)=

(8)

式中：ρ=[xre,yre,zre]T。为了方便起见，省略下标ECEF，即量测和协方差分别为zk，Rk。如无特殊申明，下文的量测及量测协方差矩阵均指转换到ECEF坐标系的量测及协方差。由此可建立如下线性的量测方程

zk=Hkxk+vk

(9)

式中：xk为k时刻的状态向量；Hk为量测矩阵。二者都由跟踪模型决定。vk为转换后的量测噪声，其协方差矩阵为Rk。采用横轴向力模型时，状态向量为xk=xCAF,k=[xyzxyzab]T，此时Hk的表达式为

(10)

至此，建立了导弹各飞行阶段滤波所需的状态方程和量测方程。由式(1)、式(2)以及式(9)可知，通过将量测转换到ECEF坐标系后，各跟踪滤波器模型的状态方程是非线性的，量测方程线性。针对非线性滤波问题，现有的方法有扩展卡尔曼滤波(EKF)、无味卡尔曼滤波[15](UKF)、粒子滤波[16](PF)、CKF以及它们的改进算法等。PF计算量较大，离工程实现较远；EKF通过在当前状态对非线性系统进行一阶泰勒级数展开来近似非线性函数本身，使非线性问题变为局部线性问题，计算量小，但系统非线性较强时，滤波精度较差；当系统非线性很强时，UKF精度好于EKF，且不用求Jacobian矩阵，但是对于高维非线性系统，对参数的选择具有一定的依赖性；CKF与UKF类似，但CKF的参数(求容积点和权值)由状态的维数唯一确定，实现更加方便，且计算量较小。综合工程实现和滤波精度，本文采用CKF进行滤波。

2 基于无偏混合估计的IMM算法

2.1 无偏混合估计

可以看到，IMM算法所采用的两个跟踪滤波器状态维数不相同，且状态变量的元素不一致，而IMM算法要实现状态和协方差的混合交互，所有状态向量必须转换成一致的状态变量，混合交互后再转换为原来维数的状态[12]。由于目标的轴向力加速度和弹道系数是弹道目标类型识别的一个重要参数，因此全系统的状态变量为

(11)

假设助推段CAF模型、被动段(PM)模型(分别为模型1、2)k时刻的状态估计值分别为

(12)

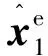
(13)

(14)

设混合概率为μi|jPr{rk=i|rk+1=j，Zk}，i,j∈{1,2,3}，Zk为直到k时刻的累积量测，则CAF模型的混合估计为

(15)

同理，PM模型的混合估计为

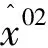
(16)

(17)

同时，根据修改后的状态向量对协方差矩阵进行相应的调整，做上述修改后，各模型的混合估计为

(18)

这样，混合后再转换为原来维数的状态作为滤波器的输入初值进行滤波就不会带来偏差，IMM算法估计也具有更好的一致性。

2.2 算法步骤

对IMM算法做如上修改后，其他与传统IMM算法相同。即可按照模型条件重初始化、模型条件滤波、模型概率更新、估计融合等步骤进行递推估计[5]，实现对导弹的稳定跟踪。图1为本文提出的ECEF坐标系下导弹连续跟踪的IMM算法原理图。

图1 IMM算法原理图

3 仿真结果与分析

实验采用MATLAB软件进行仿真计算，设计了两个典型的跟踪场景，即助推段和中段交接处的跟踪以及中段和再入段交接处的跟踪。弹道仿真采用四阶龙格库塔积分法外推生成标准弹道，雷达量测采用在弹道数据基础上加量测噪声。雷达的测距精度为σR=50 m，测角精度σA=σE=1 mrad，且量测噪声服从高斯分布，整个跟踪过程中雷达的测距和测角精度保持不变。

3.1 仿真场景1

以某近短程单级助推弹道导弹为跟踪对象，导弹发射点为东经0°，北纬30°，导弹发射方位角为80°，导弹的关机点时刻为85 s，目标的弹道系数为5 000 kg/m2，并假设保持不变。雷达布站为东经3.6°，北纬31°。图2～图4分别给出ECEF坐标系下导弹的弹道曲线，以及导弹的加速度大小和速度大小变化曲线。雷达在导弹发射35 s后发现目标，跟踪雷达数据率为1 Hz，采样点数为265。

图2 ECEF坐标系下导弹的弹道曲线

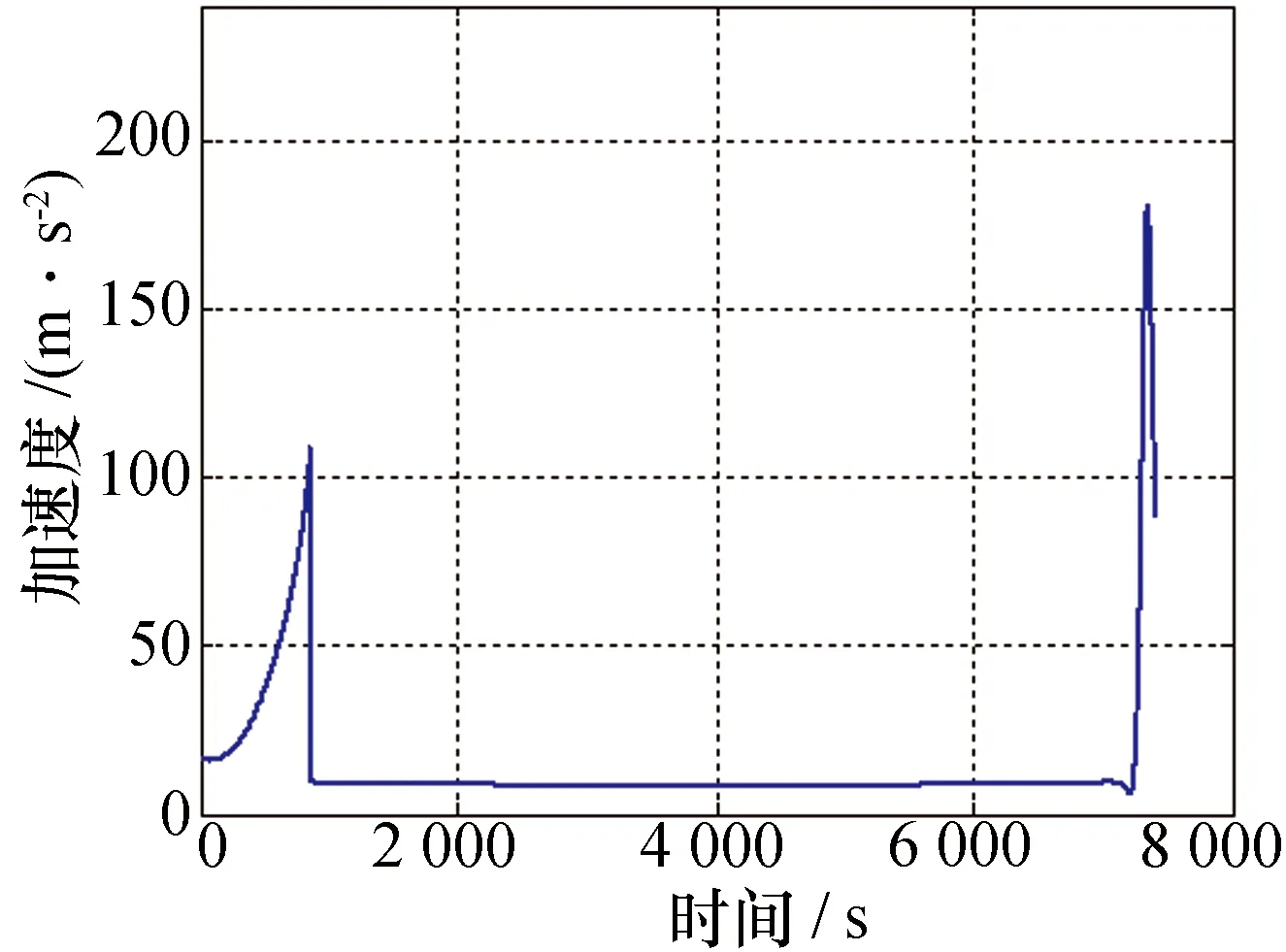
图3 目标的加速度变化曲线

图4 目标的速度变化曲线

由于助推段的机动性较强，为了验证本文算法的优越性，在同等条件下与跟踪机动目标性能较好的Singer模型算法、CS模型算法进行了比较，同时与文献[3]提出的弹道导弹连续跟踪方法进行跟踪效果对比分析。根据导弹的运动特点，IMM算法的概率转移矩阵采用如下设计

(19)

其他参数设置为：模型先验概率u0=[1/2, 1/2]T；CAF模型参数设置：轴向力加速度过程噪声qa=10 m2·s-4，相对质量燃烧率过程噪声为qb=10-8，运动加速度过程噪声为qv1=1m2·s-4。PM模型的加速度过程噪声为qv2=0.01 m2·s-4，空气阻力参数噪声为10-10。Singer模型算法参数设置：自相关时间常数为1/20，最大加速度为amax=100 m/s2，最大加速度概率为0.25，最小加速度概率为0.45。CS模型的自相关时间常数为1/20，最大加速度为amax=100 m·s-1，a-max=-50 m·s-2。

采用上述四种方法分别对仿真场景中的弹道导弹进行跟踪，并采用三点初始化方法[17]，其中，CAF模型中的轴向力加速度a的初值可以由初始状态加速度的模值确定，相对质量损耗率b的初始值设为0。PM模型以及文献[3]方法的空气阻力参数初值设为1/6 000。以均方根误差为性能评价标准，Monte Carlo仿真实验100次。

图5a)、图5b)显示的是本文方法和文献[3]方法IMM算法单次实验时模型概率随时间变化图。可以看到，导弹在助推段飞行时，CAF模型起主导地位，模型概率接近1；而导弹关机后过渡到中段飞行，CAF模型概率迅速减小到接近0，而PM模型概率迅速增大到1附近，且一直保持不变。文献[3]方法的模型概率变化与本文大致相同，但相对来说本文方法的模型概率更加合理，模型切换也更加迅速。图中分别给出了两种算法模型切换完毕的时间，可以计算出本文方法模型切换的过渡时间为6 s左右，而文献[3]方法则需要15 s左右的时间。此外关机点检测和估计具有重要意义，而通过本文IMM算法的模型概率的切换也可以用来检测关机点时刻，即模型占优切换前助推段CAF模型概率减小而中段PM模型概率同时增大的时刻可判为关机点时刻。

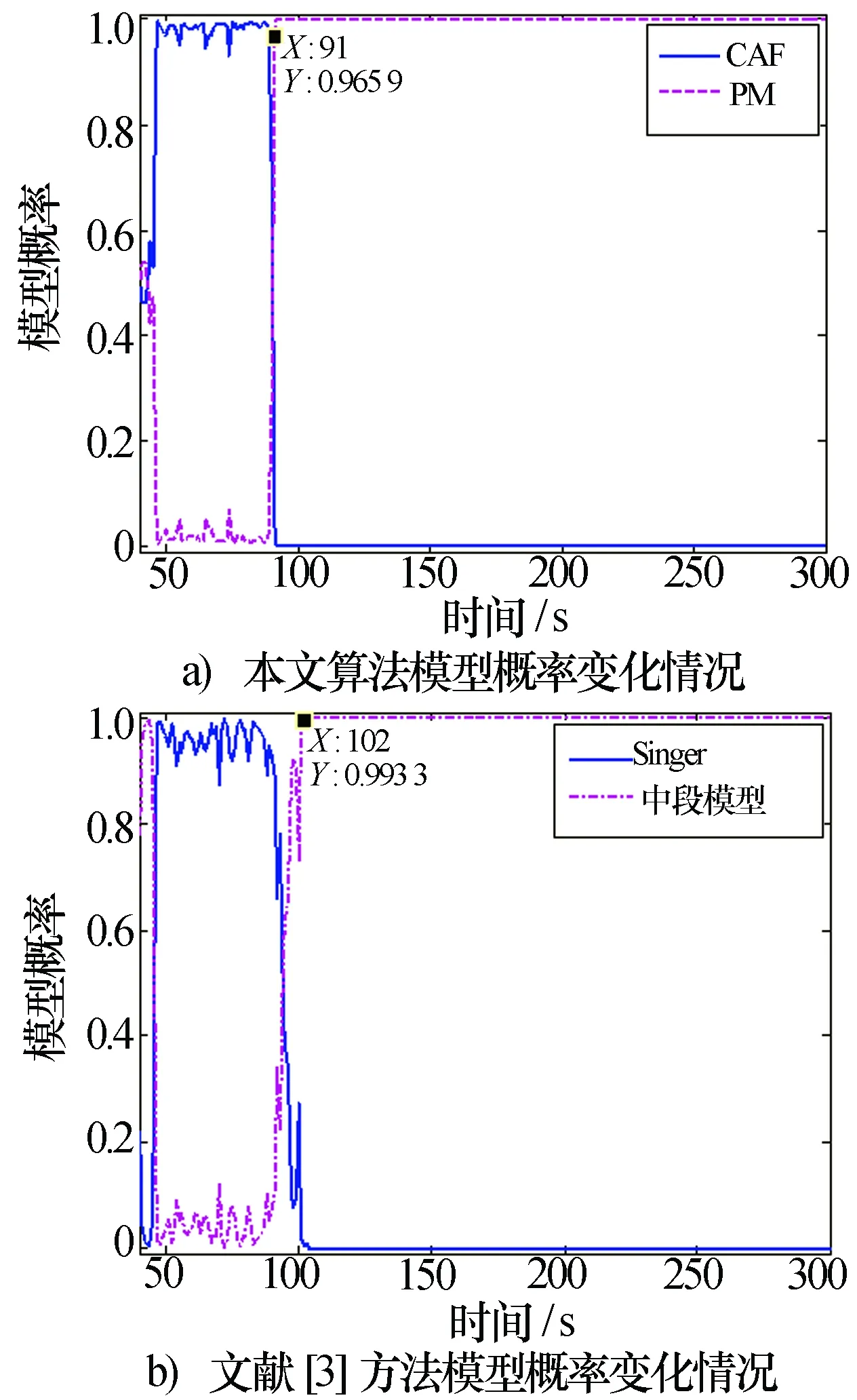
图5 模型概率变化

接下来分析各算法的跟踪误差。图6a)、图6b)分别显示了这四种算法的位置和速度均方根误差曲线，表1给出了各算法观测时间内的平均估计误差。表1表明：本文方法的平均误差最小。从图6中可以得出如下结论：

(1)助推段由于目标距雷达较远，且机动性较强，四种算法的跟踪精度都不是太高，但相对来说，本文方法的跟踪精度远好于其他三种方法，模型与助推段匹配较好。

(2)导弹关机进入中段飞行，本文方法和文献[3]方法跟踪误差迅速减小，最后收敛到一个较小的值，且两种方法在中段的跟踪精度基本相当。但由于本文方法采用精确的椭球模型对重力加速度建模，同时采用CKF作为跟踪滤波器，跟踪精度稍高于文献[3]采用圆球模型对重力加速度建模，UKF作为滤波器的方法。单模型算法中，Singer模型算法和CS模型算法在中段的跟踪误差仍比较大，跟踪误差是多模型方法的几倍。这是由于中段导弹目标的机动性较弱，而仿真中Singer模型算法和CS模型算法的参数设置主要是针对助推段进行设计的，保证在连续跟踪中滤波器不会发散，而这导致过程噪声协方差矩阵值较大，导致跟踪精度低。这也是单模型算法的弊端所在，很难设置统一的参数，使其能适应多种机动场景。另外CS模型算法在导弹关机处误差增大明显，容易导致滤波器发散甚至造成目标丢失。

(3)对于助推段和中段的连续精确跟踪来说，采用交互式多模型方法具有单模型方法不可比拟的优势，但综合来说，本文方法具有更好的性能，尤其在助推段跟踪精度远好于文献[3]方法。

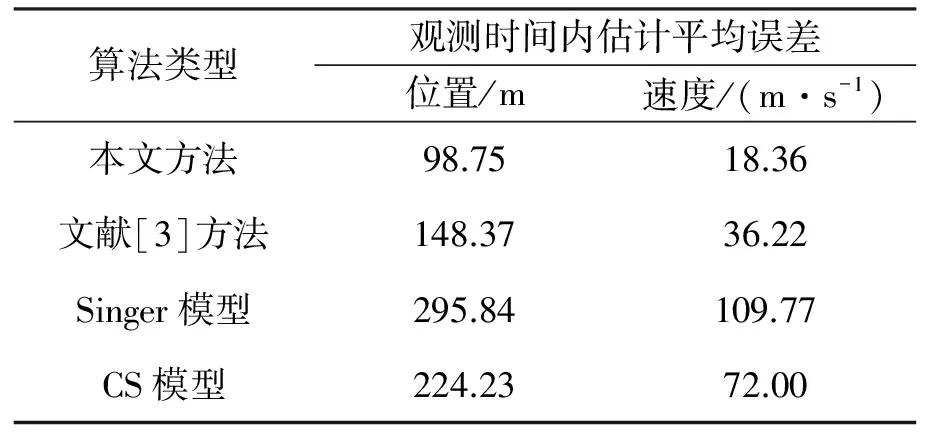
算法类型观测时间内估计平均误差位置/m速度/(m·s-1)本文方法98．7518．36文献[3]方法148．3736．22Singer模型295．84109．77CS模型224．2372．00

此外，本文算法还能对轴向力加速度大小进行估计，图7给出了单次实验的各时刻轴向力加速度大小的估计，可以看出，本文方法基本能准确估计出轴向力加速度的大小。

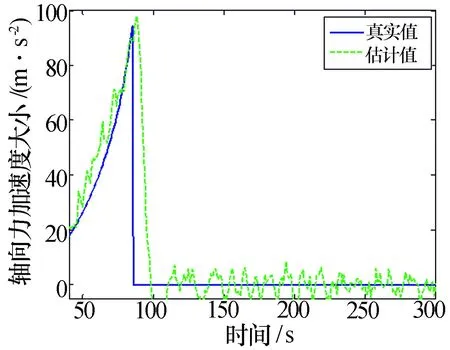
图7 轴向力加速度大小估计

3.2 仿真场景2

仍以仿真场景1中的目标为跟踪对象，雷达布站在导弹落点附近，跟踪开始的时刻为弹道发射后的第600 s，跟踪数据率为2 Hz，采样点数为272。

由于再入段目标状态方程的非线性较强，此仿真场景下重点比较几种非线性滤波算法的性能。记本文采用修正的无偏量测转换，CKF作为滤波器的弹道导弹连续跟踪的交互多模型算法为U-IMM-CKF算法，而采用EKF、UKF作为滤波器的算法记为U-IMM-EKF和U-IMM-UKF算法。同时为了分析采用无偏量测转换和未采用无偏量测对滤波的影响，与不采用无偏量测转换的被动段CKF(记为C-CKF)算法进行了比较(由于不采用无偏量测转换时，IMM算法性能很不稳定，故直接与被动段模型进行对比)。此外，与文献[3]方法的跟踪效果也进行了对比分析。

采用上述五种方法对上述目标进行跟踪，算法参数设置不变，滤波器初始化方法同仿真1，Monte Carlo仿真100次，仿真结果如图8所示。

图8的实验结果表明：

(1)当空气阻力较小时，系统非线性较弱，三种非线性滤波算法滤波性能基本相当。而目标重返大气层进入再入段，空气阻力迅速增大，系统的非线性增强，EKF的滤波性能下降，滤波精度要差于CKF和UKF算法。CKF与UKF的滤波精度基本相当，但UKF对参数选择具有一定的依赖性，否则容易造成数值不稳定问题。

(2)目标距雷达较远时，不采用无偏量测转换将产生较大的转换误差，造成跟踪精度差。随着目标离雷达距离减小，转换误差减小，对滤波性能的影响减轻。

(3)文献[3]采用弹道系数已知的六维再入段模型对目标进行跟踪，可以看到，无目标弹道系数的先验信息的情况下，此算法在再入段的跟踪误差急剧增大。而本文采用七维的再入段跟踪模型，采用对目标状态和弹道系数进行联合估计的方法，即使无先验信息，也能实现对再入目标的精确跟踪。

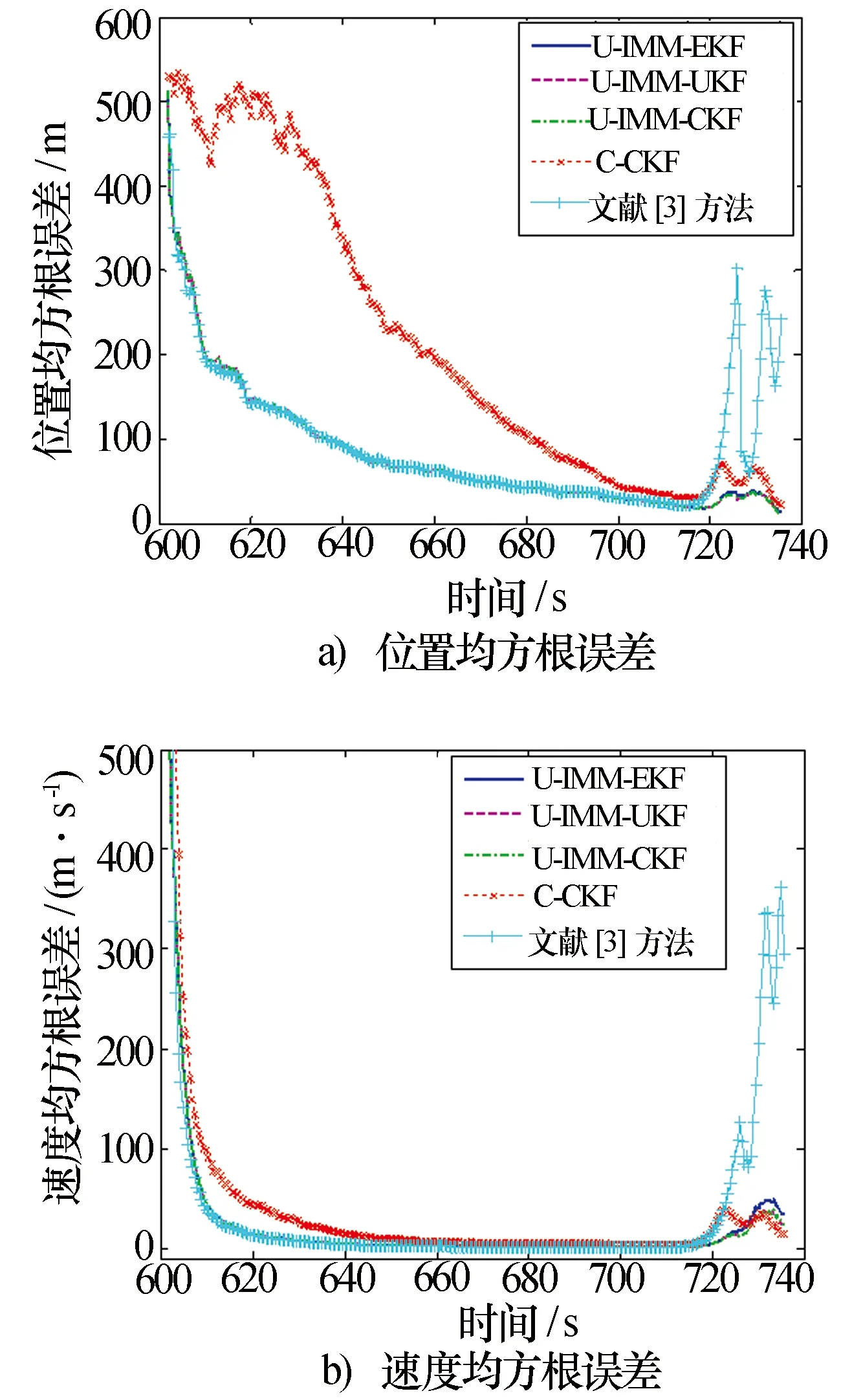
图8 均方根误差

4 结束语

针对导弹连续跟踪问题，提出了一种ECEF坐标系中弹道导弹全阶段连续跟踪的交互式多模型算法。仿真结果表明，该算法相对其他算法具有良好的连续跟踪性能，其采用的CKF滤波器具有较高的跟踪精度和数值稳定性，且通过IMM算法模型概率的变化能对导弹的关机点进行检测。此外，本文提出算法还能实现对目标轴向力加速度和弹道系数的估计。当然，本文算法仍存在不足，表现在估计误差在关机点处有一定增大，这是下一步需要改进的地方。

[1] LI X R, JILKOV V P. Survey of maneuvering target tracking, part II: motion models of ballistic and space targets[J]. IEEE Transactions on Aerospace and Electronic Systems, 2010, 46(1): 96-119.

[2] BENAVOLI A, CHISCI L, FARINA A. Tracking of a ballistic missile with a-priori information[J]. IEEE Transactions on Aerospace and Electronic Systems, 2007, 43(3): 1000-1016.

[3] 钮俊清, 单 奇, 任清安, 等. 跟踪弹道导弹全阶段的可变多模型方法[J]. 雷达科学与技术, 2011, 09(3): 224-231. NIU Junqing, SHAN Qi, REN Qingan, et al. A new algorithm with variable-structure multiple model for tracking ballistic missile at entire flight stages[J]. Radar Science and Technology, 2011, 09(3): 224-231.

[4] FARRELL W. Interacting multiple model filter for tactical ballistic missile tracking[J]. IEEE Transactions on Aerospace and Electronic Systems, 2008, 44(2): 418-426.

[5] LI X R, JILKOV V P. Survey of maneuvering target tracking, part V: Multiple-model methods[J]. IEEE Transactions on Aerospace and Electronic Systems, 2005, 41(4):1255-1321.

[6] 鲜 勇, 郑晓龙. 弹道导弹攻防仿真系统建模[M]. 北京：国防工业出版社，2013. XIAN Yong, ZHENG Xiaolong. Modeling of ballistic missile attack defense simulation system[M]. Beijing: National Defense Industry Press, 2013.

[7] LI X R, JILKOV V P. A survey of maneuvering target tracking, part III: Measurement models[J]. Proceedings of SPIE Conference on Signal & Data Processing of Small Targets, 2001, 4473(11): 423-446.

[8] 赵艳丽, 李 宏, 高向东, 等. 不同坐标系下中段弹道目标跟踪算法研究[J]. 现代雷达, 2011, 33(5): 54-59. ZHAO Yanli，LI Hong，GAO Xiangdong, et al. A study on ballistic target tracking in midcourse of various coordinate systems[J]. Modern Radar, 2011, 33(5): 54-59.

[9] DUAN Z S, HAN C Z, LI R X. Comments on“Unbiased converted measurements for tracking”[J]. IEEE Transactions on Aerospace and Electronic Systems, 2004, 40(4):1374-1377.

[10] 李 为, 李一平, 封锡盛. 基于卡尔曼滤波预测的无偏量测转换方法[J]. 控制与决策, 2015, 30(2): 229-234. LI Wei, LI Yiping, FENG Xisheng. Tracking with prediction-conditioned unbiased converted measurements[J]. Control and Decision, 2015, 30(2):229-234.

[11] ARASARATNAM I, HAYKIN S. Cubature Kalman filters[J]. IEEE Transactions on Automatic Control, 2009, 54(6): 1254-1269.

[12] BLACKMAN S S, POPOLI R. Design and analysis of modern tracking systems[M]. Boston: Artech House, 1999.

[13] GLASS J D, BLAIR W D, BAR-SHALOM Y. IMM estimators with unbiased mixing for tracking targets performing coordinated turns[C]// 2013 IEEE Aerospace Conference. [S.l.]: IEEE Press, 2013: 1-10.

[14] CARDILLO G P, MRSTIK A V, PLAMBECK T. A track filter for reentry objects with uncertain drag[J]. IEEE Transactions on Aerospace and Electronic Systems, 1999, 35(2): 394-409.

[15] 占荣辉, 郁春来, 万建伟. 简化UKF算法在单站无源目标跟踪中的应用[J]. 现代雷达, 2007, 29(3): 42-46. ZHAN Ronghui, YU Chunlai, WAN Jianwei. Aplication of smiplified UKF algorithm to single observer passive target tracking[J]. Modern Radar, 2007, 29(3): 42-46.

[16] 程水英, 张剑云. 粒子滤波评述[J]. 宇航学报, 2008, 29(4): 1099-1111. CHENG Shuiying, ZHANG Jianyun. Review on particle filters[J]. Journal of Astronautics, 2008, 29(4): 1099-1111.

[17] BAR-SHALOM Y, LI X R, KIRUBARAJAN T. Estimation with applications to tracking and navigation: theory algorithms and software[M]. New York: John Wiley & Sons, 2001.

许登荣 男，1991年生，硕士研究生。研究方向为雷达数据处理。

程水英 男，1974年生，副教授。研究方向为机动目标跟踪、软件无线电、信号与信息处理。

包守亮 男，1993年生，硕士研究生。研究方向为雷达数据处理。

A Study on Ballistic Missile Tracking in ECEF Coordinate System

XU Dengrong，CHENG Shuiying，BAO Shouliang

(504 Laboratory of Electronic and Engineering Institute, Hefei 230037, China)

Aiming at the problem that single model tracking algorithm can not track the ballistic missile accurately, an interacting multiple model (IMM) algorithm is proposed in Earth-centered Earth-fixed coordinate for continuously tracking the missile for all the flight stage. According to the force condition in different stages of trajectory, the corresponding tracking model is established. The axial force of target almost keep constant in boost phase, the constant axis force model is adopted; coast and reentry phase use the passive phase tracking model to track the missile. Both the models use the cubature Kalman filter algorithm to filter. In view of the problem that a bias is caused in the mixing stage of this IMM algorithm, an unbiased mixing method is adopted. The simulation results verify the superiority of the algorithm.

maneuvering target tracking; ballistic missile; interacting multiple model algorithm; cubature Kalman filter

10.16592/ j.cnki.1004-7859.2016.11.012

国家自然科学基金资助项目(61201379)；安徽省自然科学基金资助项目(1608085MF123)

许登荣 Email：xudengrong@126.com

2016-08-15

2016-10-17

TN957.51

A

1004-7859(2016)11-0053-08