求多面体体积的六种常用技巧

黄光鑫●

四川师范大学附属中学高中部(610066)



求多面体体积的六种常用技巧

黄光鑫●

四川师范大学附属中学高中部(610066)

无论在数学的平时考试或者高考中经常会出现求多面体体积的题目，尤其是文科高考题，经常在立体几何的大题中出现求体积的小问.有的学生由于缺乏求体积的技巧而失分，甚为可惜！下面我们系统总结求多面体体积的几种常用技巧供大家参考.

一、换底

例1 (2014年福建文科(19))如图1，三棱锥A-BCD中，AB⊥平面BCD，CD⊥BD.

(1)求证：CD⊥平面ABD；(2)若AB=BD=CD=1，M为AD中点，求三棱锥A-MBC的体积.

解析1 (1)∵AB⊥平面BCD，CD⊂平面BCD，

∴AB⊥CD，又∵CD⊥BD,∴CD⊥平面ABD.

(2)若以△MBC为底面求三棱锥A-MBC的体积，不仅ΔMBC的面积不好计算，而且A点到平面MBC的距离即三棱锥A-MBC的高更不好计算，所以考虑换底：选择以MAB为底面的话，CD就是三棱锥的高，容易求得：

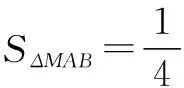
问题迎刃而解.

点评 换底是求三棱锥体积最常用的一种技巧.

二、分割

例2 (见前面例1)

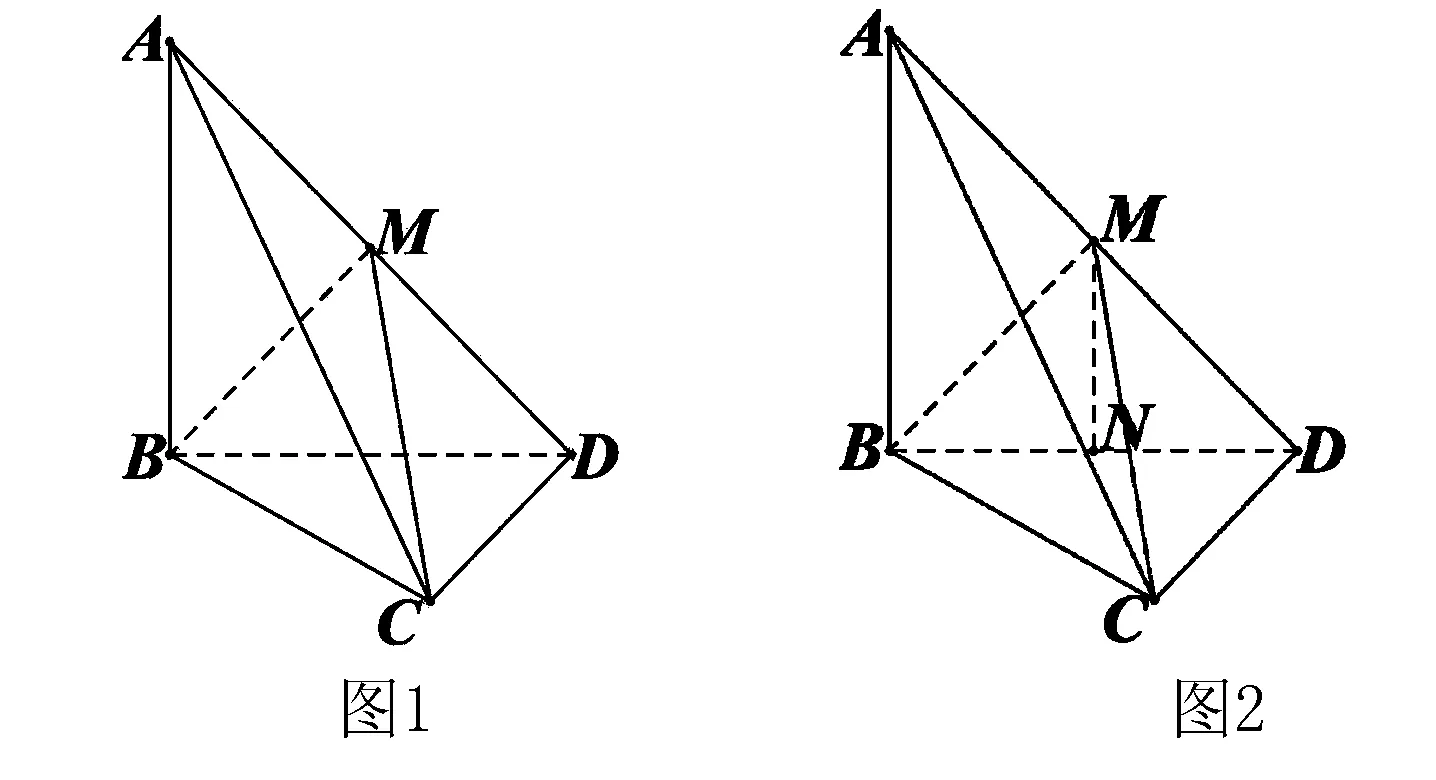
解析2 (1)略.(2)也可以将三棱锥A-MBC

看作一个大的三棱锥A-BCD切掉了一个小的三棱锥M-BCD而成的.于是可以作MN⊥BD于N，显然MN⊥平面BCD，如图2.

所以VA-MBC=VA-BCD-VM-BCD

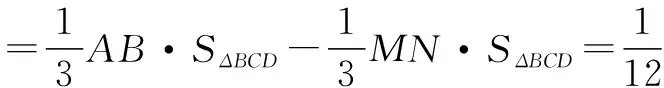
例3 如图3，在三棱柱的侧棱A1A和B1B上各有一动点P,Q，且满足A1P=BQ，过P、Q、C三点的截面把棱柱分成两部分，则其体积之比为( ).

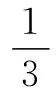
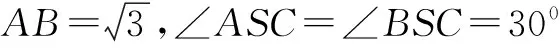
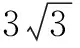
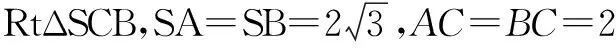
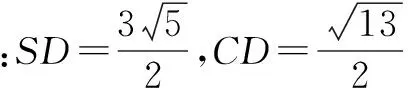
在ΔSCD中，由余弦定理可得：

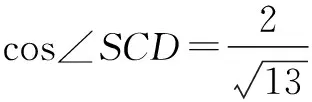
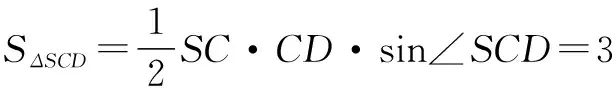
于是VS-ABC=VA-SCD+VB-SCD

选C.

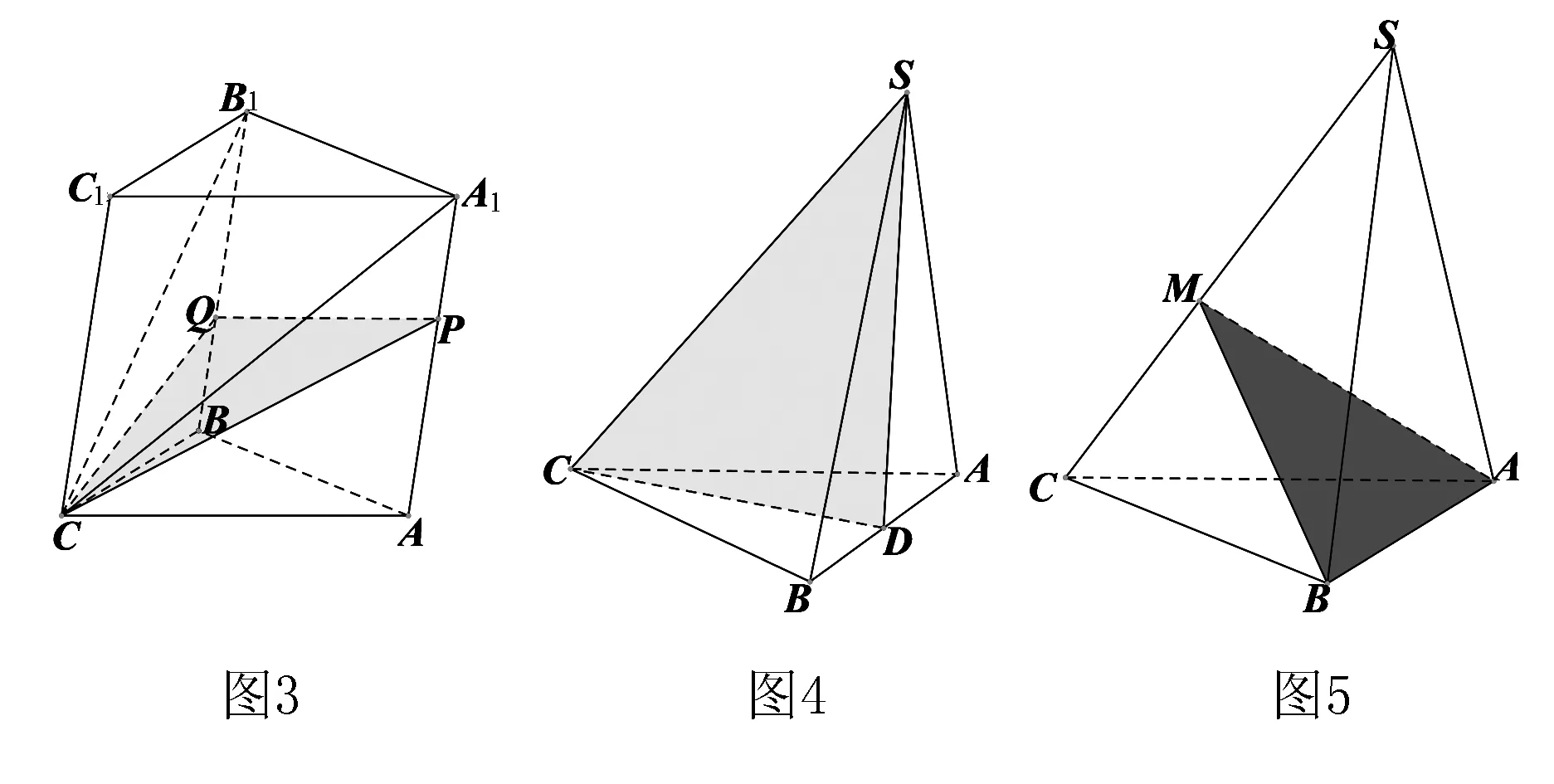
点评 第二种分割方法显然比第一种分割方法运算量要小得多.抓住了图形和数字的特殊性找到的分割方法更优越.

三、补形

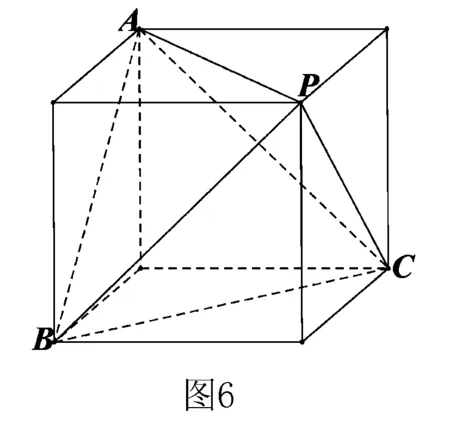
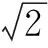
解析1 以正方体的面对角线为棱可构成一个正四面体，所以可将原正四面体还原补成一个棱长为1的正方体，此正方体、正四面体的顶点在同一球面上(如图6)，从而球的直径等于正方体的体对角线，即：

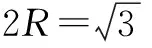
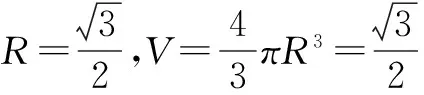
四、特殊化

例6 (见前面例3)

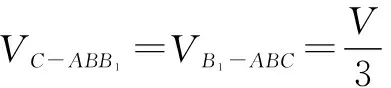
五、估算

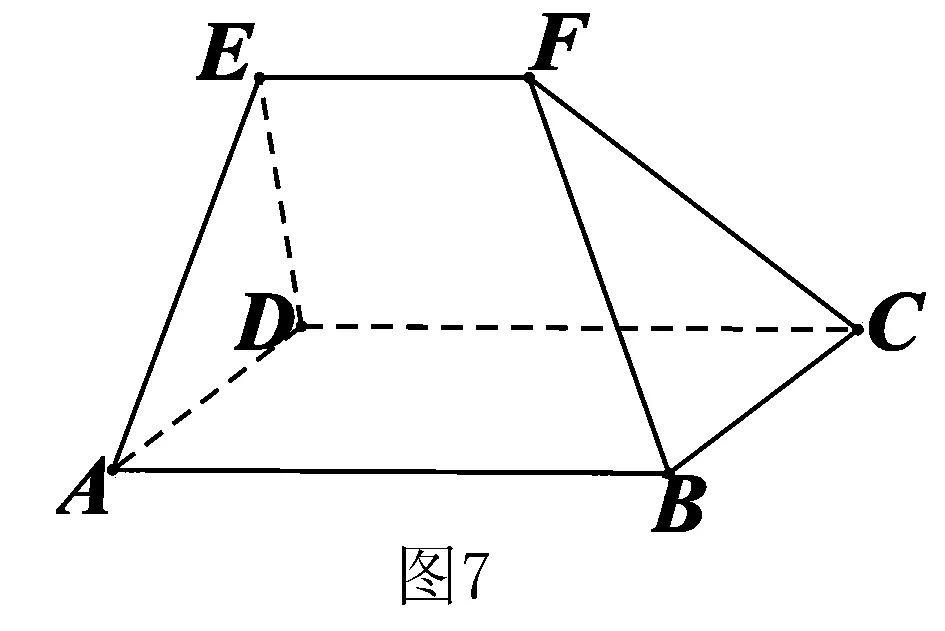
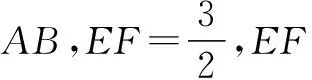
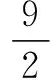
解 连接EB,EC.因为

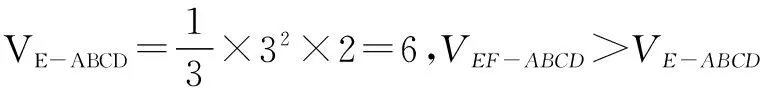
所以排除A、B、C,选D.

六、转化

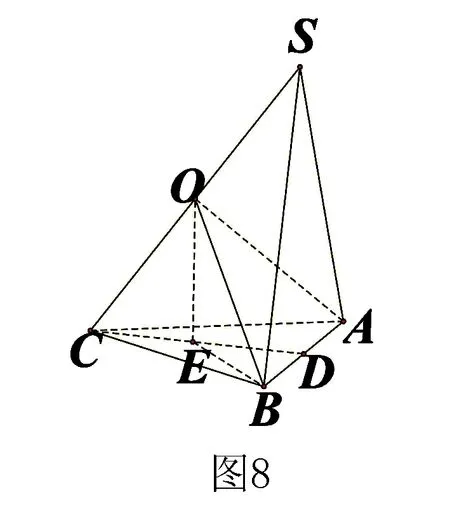
例8 (见前面例4)

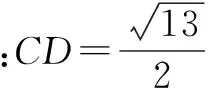
例9 正六棱锥中，G为PB的中点，则三棱锥D-GAC与三棱锥P-GAC的体积之比为( )

A．1∶1 B．1∶2 C．2∶1 D．3∶2

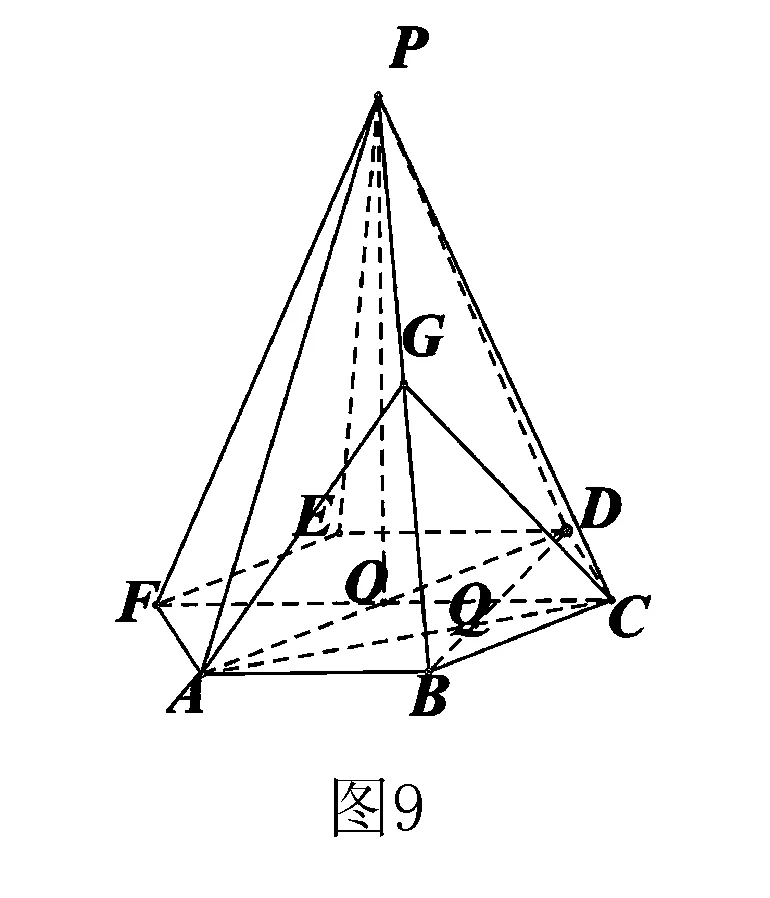
解析 三棱锥D-GAC与三棱锥P-GAC的底面积相同，所以它们的体积之比就等于高之比，∵G为PB的中点,∴P点到平面GAC的距离等于B点到平面GAC的距离,于是可进行第一次转化:VP-GAC=VB-GAC，据平面几何知识容易知道：DQ=2BQ∴D点到平面GAC的距离等于B点到平面GAC的距离的2倍，于是可以进行第二次转化：

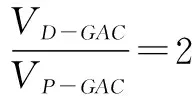
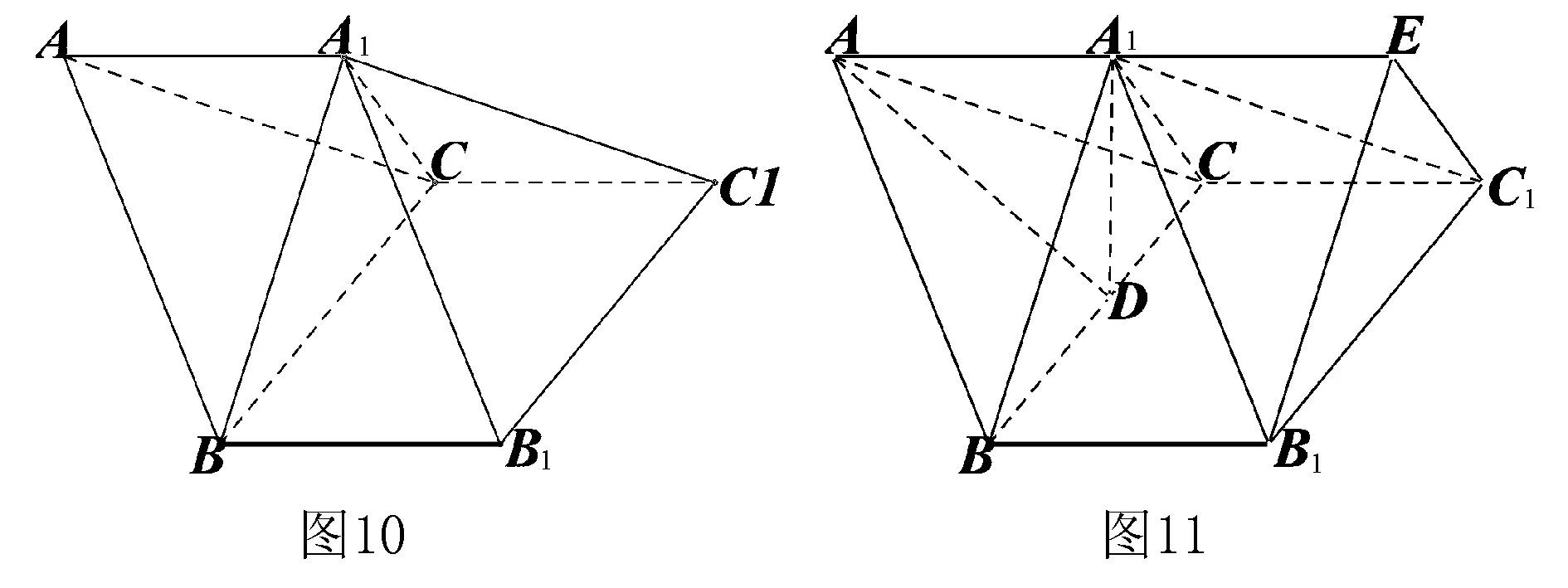
例10 (2014年江西文科(19))如图10，三棱柱ABC-A1B1C1中，AA1⊥BC,A1B⊥BB1.

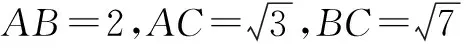
何值时，三棱柱ABC-A1B1C1体积最大，

并求此最大值.

解析1 (1)由AA1⊥BC知BB1⊥BC，

又∵A1B⊥BB1∴BB1⊥平面A1BC，∵BB1∥CC1，CC1⊥平面A1BC，从而A1C⊥CC1.

(2)计算斜三棱柱ABC-A1B1C1的体积需要知道它的高，求三棱柱的高并不容易，而据(1)可知CC1⊥平面A1BC，所以考虑割补法：将原三棱柱以面A1BC进行分割，将切下的三棱锥A1-ABC的面ABC与四棱锥A1-BCC1B1的侧面A1B1C1重合，由此补成一个直三棱柱A1BC-EB1C1(如图11).

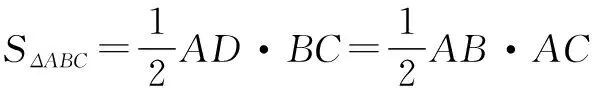
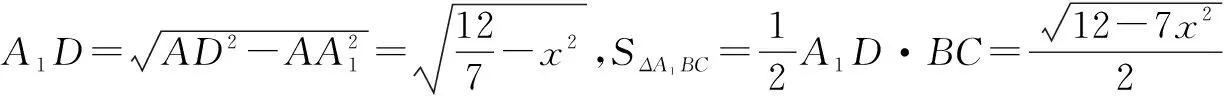
解析2 (1)略.(2)计算斜三棱柱ABC-A1B1C1的体积需要知道它的高.

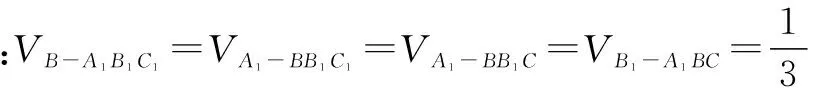
∴VABC-A1B1C1=3VB-A1B1C1=SΔA1BC·BB1，后面同解析1.

点评 解析1是将斜三棱柱转化为直三棱柱来解决.解析2是将斜三棱柱转化为三棱锥通过换底来解决.殊途同归！

通过以上各例可以看出求多面体体积的常用技巧有六种：(1)换底；(2)分割；(3)补形；(4)转化；(5)估算；(6)特殊化.只要我们根据几何体的不同特征，灵活的运用以上各种技巧，求多面体的体积就再也不会有什么障碍了.

G632

B

1008-0333(2016)28-0002-02