正确使用极值法解决物理问题
2016-12-16江苏省南京科技职业学院210048
江苏省南京科技职业学院(210048)
魏 樱●
南京育英第二外国语学校(210044)
鲁佩用●
正确使用极值法解决物理问题
江苏省南京科技职业学院(210048)
魏 樱●
南京育英第二外国语学校(210044)
鲁佩用●
本文通过对中考题学生两种解析方法的对比,引出如何正确使用极值法,在通过对部分典型示例进行理论推导和图像分析后顺利解决这一问题.
极值法;两极端;实例
在平时的教学中,常遇到“极值”问题,但多数教师都是通过数学方法进行分析.不仅要求学生具有较好的物理基础,更需具有较高的数学应用能力,如果教师能教给学生灵活运用物理的思想和方法去解决问题,这对提升学生的物理思维和物理素养不无裨益.
一、中考原题
如图1所示,两个完全相同的量筒里分别盛有质量相等的水和酒精,A、B两点到量筒底部的距离相等,则A、B两点受到液体的压强pA和PB的大小关系是 ( ).
A. pA>pBB.pA 学生1(常规法):假设液体的总重力都为G,液体密度分别为 A和B,且 A>B,量筒的横截面积均为S,A、B两点距量筒底的距离都为h,图2中,A、B两点以上液体的重力,即阴影部分液体的重力分别为GA和GB,则 由①②两式及ρA>ρB得pA 学生2(极值法): A、B 两点距底部的距离相同,具有随意性,可假设 A、B 两点在甲容器的液面高度上(如图 3),此时pA=0,pB>0,所以pA 从以上两种方法可以看出,在解决物理问题时,当一个物理量或物理过程发生变化时,运用“极值法”对其变量作合理的延伸,把问题推向极端,往往会使问题化难为易,达到“事半功倍”的效果.那么如何正确使用极值法呢? 如图4所示,甲、乙两个质量相等的均匀实心正方体放在水平地面上,已知铜的密度大于铁的密度,若沿水平方向分别截去体积相等的部分,则剩余部分对水平面的压强p甲和p乙的大小关系是 ( ). A. p甲>p乙B.p甲 极值法:假设将甲全部消去,则剩余部分对水平面的压强p甲=0和p乙>0,因此,该题选择B.事实果真如此吗? 正确使用极值法:假设截去的体积趋向为0,则剩余部分对水平面的压力基本相同,所以压强p甲>p乙;若将甲全部消去,则剩余部分对水平面的压强p甲 为何例1采用极值法时不用考虑另一极端呢,根据①②两式,可画出压强-高度图像,如图7所示,由图像可以看出,A、B两点受到液体的压强pA和PB都随高度h的增大而减小,pA先减小到0,并且始终pA 由前面的分析可以看出,使用极值法解决物理动态变化问题时,是否需要考虑两极端,取决于所求物理量随动态变化物理量变化而变化时,是否有确定的大小关系.如果有确定的大小关系只需考虑一个极端,否则,就需要考虑两极端.当然,在不知道是否需要考虑另一极端的情况下,我们可以对两极端都进行考虑,再进行判断. 如图8所示电路,电源电压保持不变,R1为定值电阻,R2为滑动变阻器(R2最大阻值大于定值电阻R1). 当开关S闭合后 (1)滑动变阻器的滑片P向右端滑动过程中,电压表示数将( ). A. 增大B. 不变C. 减小D. 无法判断 (2)滑动变阻器的滑片P向右端滑动过程中,滑动变 阻器R2消耗的电功率将( ). A. 增大B. 不变 C. 减小D. 先增大后减小 第(1)问,当滑片P处在滑动变阻器最左端时,变阻器接入电路的电阻为零,相当于电压表接在一根导线的两端,故示数为零.由R2最大阻值大于定值电阻R1,可假设R2最大阻值 ,当滑片P滑动到最右端时,电压表示数接近电源电压,达到最大值.因此,电压表的示数由无变有,由小变大,该问选择A. 第2问,当滑片P处在滑动变阻器最左端时,电压表示数为零,滑动变阻器消耗的功率也为零;当滑片P滑动到最右端时,仍假设R2最大阻值 ,电压表示数接近电源电压,由P=U2/R得到,此时滑动变阻器消耗的功率→0.由此可以判断出滑动变阻器消耗的功率必然先变大后减小.因此,该题选D. 用极值法解决物理问题时,不仅给学生解决问题多提供一条思路,还可以让复杂的问题简单化,特别是做客观题时往往会取得事半功倍的效果.但如果搞不清极值法的正确使用方法,就会出现错误的结果. G B
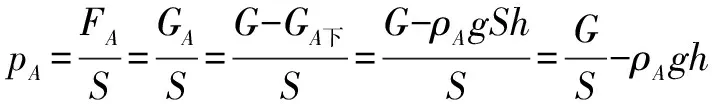

二、极值法正确使用过程分析

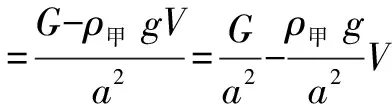
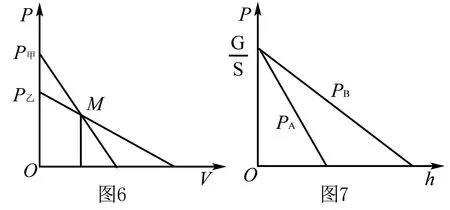

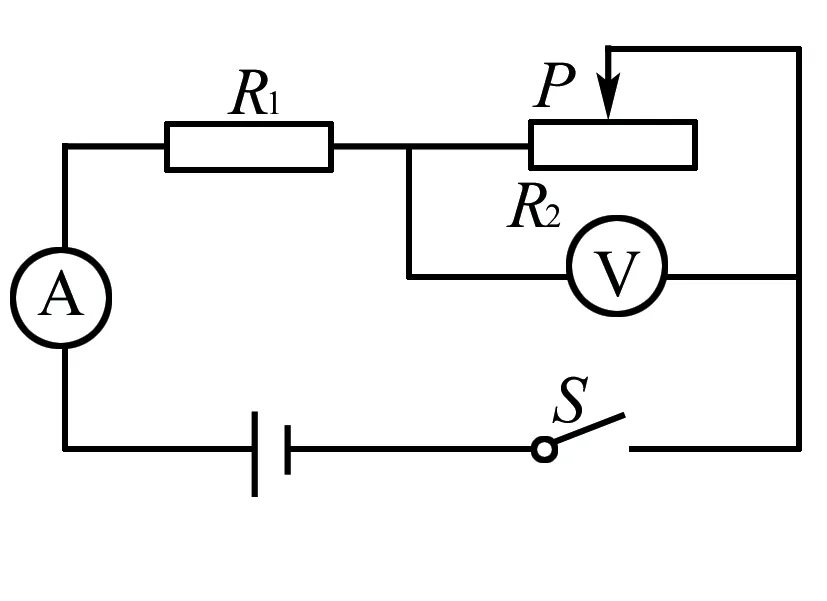
三、极值法应用实例
