初中数学函数题解题技巧探究
2016-12-16江西省赣州市章贡中学341000
江西省赣州市章贡中学(341000)
蔡 珉●
初中数学函数题解题技巧探究
江西省赣州市章贡中学(341000)
蔡 珉●
在初中数学课程体系中,函数内容是很重要的一个模块,在中考试题中,这部分内容是考查的重点.本文专就初中数学函数的解题技巧进行适当探究,以期能够为学生们解题提供一定的指导.
初中数学;函数题;解题技巧;探究
一、解答函数题所必要的基本条件
(一)基础知识足够扎实
要想学好初中数学,其基本前提是要对基础知识掌握得非常牢固.因此在日常课堂教学中应当特别注意学生对基本概念的理解与记忆.可以想象,学生们如果在平时的学习中对基本概念理解得不够深入透彻,解题时,就会出现错误.所以,老师们在进行基础概念教学中要特别注意,对于那些关键字要特别强调,能够加深学生的理解.
(二)公式定理运用足够灵活
很明显,无论怎样解答题目,教材中的公式及定理必然会运用得到.一方面,这些公式定理属于基础知识范畴,是学生进行初中数学学习的基础内容;另一方面,也是学生进行数学学习的标准与参照.所以,学生要想解题顺畅,就必须牢固掌握公理、公式,并能够做到灵活运用.对公式定理进行仔细研究后我们发现,初中阶段的公式公理的主要构成就是逻辑用语与字母符号,感情色彩全无,读起来都不是很顺口,因此要想牢牢记住,确实具有一定难度,唯有不断练习巩固,方能记住.
二、具体解题技巧
(一)待定系数法
除了简单的公式法和分类法外,待定系数法在解决函数求值问题时,具有很强的使用性,不管是一次函数、二次函数,还是反比例函数,在遇到求值问题时,运用待定系数法,一般都会收到立竿见影的效果,下面用一个小例子加以说明:
例1 已知点(-2,-3)、点(3,5)和点(2,1)在一个二次函数图象上,求当x=5时的函数值.
分析 先通过待定系数法设置出y=ax2+bx+c,再代入题目所给的三个点,能够很容易求出a,b,c三者的值,该函数解析式自然而然也就出来,最后令x=5,代入所求的解析式中,很容易就能确定此时的函数值大小,以上分析过程也就待定系数法的基本解题思路.
(二)数形结合法
前面提到,函数问题很多时候都是与图象相结合的,所以在解决很多函数问题时,需要运用到这种方法.数学家华罗庚曾经用一句经典语句来形容该法的重要性,即数无形,不具体;形无数,难入微.在解答初中函数题型时,有时候,通过数形结合法,往往会使抽象很难的问题变得具体简单化,达到事半功倍的效果.就拿二次函数y=-(x-h)2+c而言,从其图象可以很明显的看到,当x
例2 已知在反比例函数y=5/x图象上存在三点,分别是A(-2,y1),B(-1,y2),C(4,y3),试比较y1,y2,y3三者的大小.
分析 在进行正式解答该题之前,一定要对反比例函数的性质非常了解,了解y随x的变化情况.
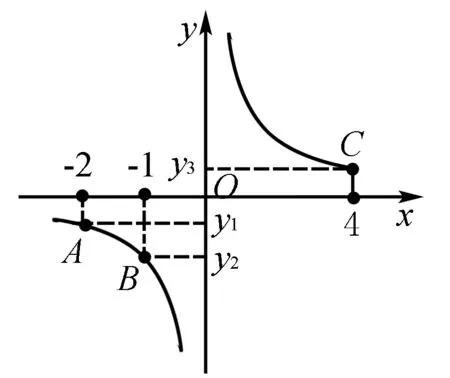
具体解答:(1)直接将三点的横坐标代入反比例函数,分别求得y1,y2,y3三者的值,并进行比较得出三者大小关系.(2)首先在直角坐标系中作出该反比例函数的图象,标上A,B,C三点的横坐标,从图中可以很明显的看出y1,y2,y3三者的大小关系.可以看出,通过画出反比例函数的图象,能够直观地看出该函数的性质.
(三)思维转换法
在进行解答初中函数类题型时,经常会遇到含未知参数的问题,学生们在解答该类题目时总是容易出现解题失误,有时候不知道从何动笔,这对学生学习函数的积极性造成很大打击,不少同学遇到挫折后会对函数感到厌烦,使得学习效益不尽人意.实际上,面对这种问题,老师要善于对学生进行引导,让他们学会进行思维转换,把题目中未知量转化为已知量,把变化的量转化为不变的量,只有这样,题目的难度才会进一步下降,学生在解答起来就会变得更容易,能够让学生的解题质量得到有效提升.下面仍通过一个例子加以说明:
例3 已知x1和x2是方程(x-2)(x-m)=(p-2)(p-m)的两根,
(1)请求出x1和x2的值是多少;
(2)如果x1和x2是某直角三角形的两个直角边,试问当m和p满足何种条件时,这个直角三角形的面积会取得最大值?并求出这个最大值.
分析 从题中我们可以看出,在方程中存在x,m,p三个未知数,一个方程,不可能解得出来,学生一般会感觉有难度,这个时候,老师就要做好引导工作,让学生把方程中m和p作为已知量,这样方程只剩下x,求解起来会变得方便得多.
[1]张贵阳.新课标下初中数学解题策略初探[J].速读(下旬), 2015(05).
[2]吴蕾.初中数学函数题解题策略探微[J].教书育人(教师新概念), 2012(3)
[3]陈彦游. 初中数学函数题的解题技巧探究[J].理科爱好者(教育教学版),2015(2)
G
B
