在变化中找不变——浅谈动态几何中利用面积的不变量关系解题

浙江省慈溪市三北初级中学(315331)

黄群晖●



在变化中找不变
——浅谈动态几何中利用面积的不变量关系解题

浙江省慈溪市三北初级中学(315331)

黄群晖●

动态几何问题，体现了近代数学运动变化的思想，是近几年数学中考命题的重点，解这类题目的一般方法是抓住变化中的“不变量”，以不变应万变.本文以利用面积的等量关系如何解题为例，浅谈动态几何中利用面积的不变量关系解法及启示.

不变量；几何动态；面积；解法启示

动态几何题，包含了一些“动态”的点、线段、直线等元素，给静态的平面几何题赋予了活力，使题意更新颖.同时“动态”的存在也使平面几何题更趋灵活，加强了对学生想像能力的考查.动态几何问题中往往有很多变量，还有很多图象、数据按一定规则进行变换和操作，这些无疑增加了问题的复杂性，给问题的解决增加了难度.但在这些复杂变化的背后总是隐藏着一些没有变化的东西，那就是不变量，抓住不变量就成了解决问题的关键.

为了大家可以清晰地了解不变量在处理几何问题的便捷，在这里我简单的举两道例题来说明.

一、利用面积不等量关系的解法

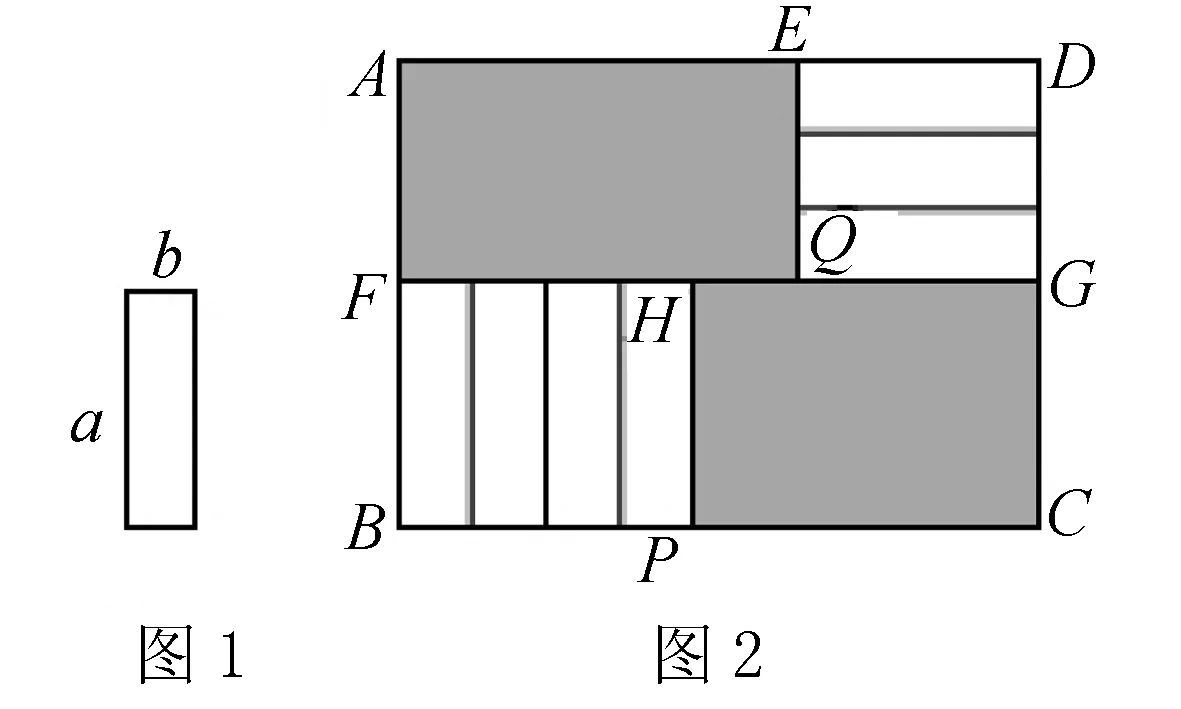
例1 (2013·宁波)7张如图1的长为a，宽为b(a>b)的小长方形纸片，按图2的方式不重叠地放在矩形ABCD内，未被覆盖的部分(两个矩形)用阴影表示．设左上角与右下角的阴影部分的面积的差为S，当BC的长度变化时，按照同样的放置方式，S始终保持不变，则a，b满足( ).

A．a=2.5bB．a=3bC．a=3.5 bD．a=4b

一般情况下的解法是：

解 左上角阴影部分的长为AE，宽为AF=3b，右下角阴影部分的长为PC，宽为a，

∵AD=BC，即AE+ED=AE+a，BC=BP+PC=4b+PC，

∴AE+a=4b+PC，即AE-PC=4b-a，

∴阴影部分面积之差S=AE·AF-PC·CG=3bAE-aPC=3b(PC+4b-a)-aPC=(3b-a)PC+12b2-3ab，则3b-a=0，即a=3b．故选B

用不变量来解题：

解 既然BC是变化的，当点P与点C重合开始，然后BC向右伸展，

设向右伸展长度为X，左上阴影增加的是3bX，右下阴影增加的是aX，因为S不变，

∴增加的面积相等，∴3bX=aX，∴a=3b．

故选B.

从上面解题过程可以得出，在动态几何教学中我们如果让学生学会用不变量来解题，学生非常容易找到等量关系，列出合适的、简便的方程，解题速度也大大加快.特别如上题作为2013年宁波数学中考的最后一题选择题，许多学生在印象中认为这题一定很难很复杂，容易产生心理上的恐惧.因此，用一般方法来解题就存在两大缺陷，第一比较费时容易使学生产生紧张心理，第二容易出现计算错误.若此题用不变量“增加的面积相等”来解此题，在中考中既安定了心神，又为后面解题引得了时间.因此，在平时教学中，我觉得让学生在动态几何中找到不变量，利用不变量来解题，是非常好的一条捷径.

二、利用面积的等量关系解题的启示

1.仔细审题，有的放矢

认真读题——俗话说得好：“读书百遍，其义自见.”对于几何语言的理解能力尚处在培养期的七年级学生而言，培养他们认真读题特别重要.它不仅是学生正确理解题意的基础，还是学生正确解决问题的根本保证.因此在几何数量关系的揭示中，涉及很多名词术语，语言叙述有顺有逆，数据显示有明显、有隐含，题目结构变化多样，因此，学生对题意的理解并非是容易的事.这就要求我们老师在训练学生读题时，要让学生学会抓关键词.

2.理解题目，理清关系.

(1)找到运动中变化的点、线、量.如上例中，我们通过审题发现，BC的长度是在不断变化的，随着此变化，左上角与右下角的阴影也是在不断变化的.

(2)找出在运动中不变的点、线、量.如上例中，小长方形的长和宽不变，左上角与右下角的阴影部分的面积的差S始终保持不变.

3.列出方程，解决问题.

在上题中，我们利用面积差S不变，那么在变化过程中，左上角和右下角增加的面积相等，以而列出“左上角增加的面积=右下角增加的面积”.

4.巩固训练，养成习惯.

叶圣陶先生说：“习惯是从实践中培养出来的，知道一点做一点，知道几点做几点.积累起来，各方面都养成习惯，而且都是好习惯，就差不多了.”在数学问题中，有许多解是符合方程的，但却不符合题意或者不符合实际生活需要，所以我们要养成验算的习惯，这样既可避免由于计算错误造成的失分，又可保证自己解题的正确性.我认为，利用面积不变量解几何动态问题还是需要一定的练习来巩固的.因此我出了下面一题来使同学们加强练习.

例2 如图,点E是边长为2的正方形ABCD的边AB的中点,点F是BC延长线的点，EF交CD与G，若四边形AEGD的面积=△CGF的面积=S，并且S△CGF÷S△BEF=(CF÷BF)2，则S=____.

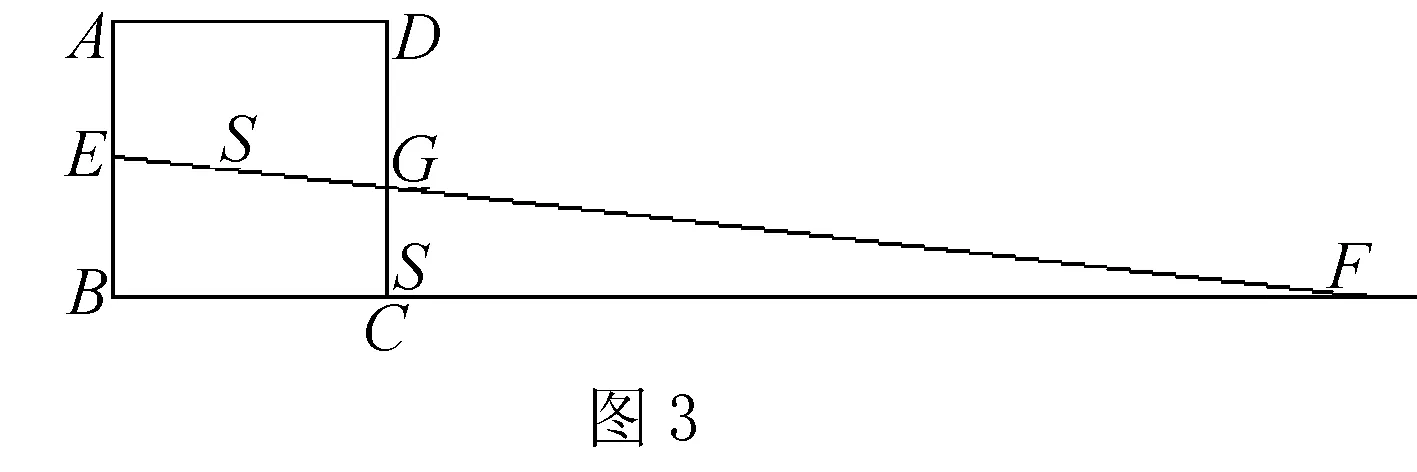
一般情况下的解法是：

解 ∵四边形AEGD的面积=△CGF的面积=S，S△CGF÷S△BEF=(CF÷BF)2.

▶▶

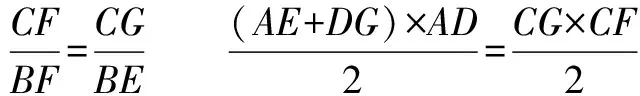
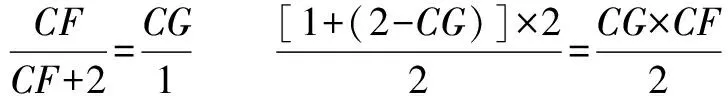
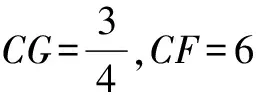
用不变量来解题：

解 ∵四边形AEGD的面积=△CGF的面积=S，

∴△BEF的面积=正方形ABCD的面积

∴BE×BF÷2=4 ∴1×(2+CF)÷2=4

∴CF=6 ∴S=(CF÷BF)2×4=2.25

此题对于七年级学生来讲是不可能用上述的一般方法来解的，因为相似和两个未知数方程对他们来说都是没有学过的.即使九年级学生解起来也比较困难，比较花时间.但七年级的学生们用四边形AEGD的面积=△CGF的面积=S，得到△BEF的面积=正方形ABCD的面积，利用不变量来解此题，一下就轻松解决了.

通过这两道例题我们可以看到，做几何动态类的题目.往往用题目中的动点、动线是很难解决的，可是利用动态中的不变量来解题就轻松、便捷了许多.通过本文的讲解以及例题的演示，我希望这篇文章能够为大家带来益处.不过，由于个人的数学知识有限，可能对于动态几何题不变量在解题中的技巧归纳不够深入，希望在以后的学习和工作中继续完善.

(1)张保利.动态型数学问题的思考路径，《中学生数理化》，2004年16期

(2)《怎样解题》美国,数学家和数学教育家G波利亚

G

B