初中数学几何推理与图形证明对策分析
2016-12-16江苏省徐州市树人初级中学221000
江苏省徐州市树人初级中学(221000)
陈晶晶●
初中数学几何推理与图形证明对策分析
江苏省徐州市树人初级中学(221000)
陈晶晶●
本文结合笔者实践工作经验,主要对学习方法进行详细介绍,并且有针对性地提出一些例题,希望能够通过例题的解析,可以让学生能够在几何推理与证明的过程中掌握更多的解题技巧.
一、反证法
逆向思维是学生在解图形题时应该具备的思维,解题的过程中,若正面不好入手,那么考虑从反面入手.
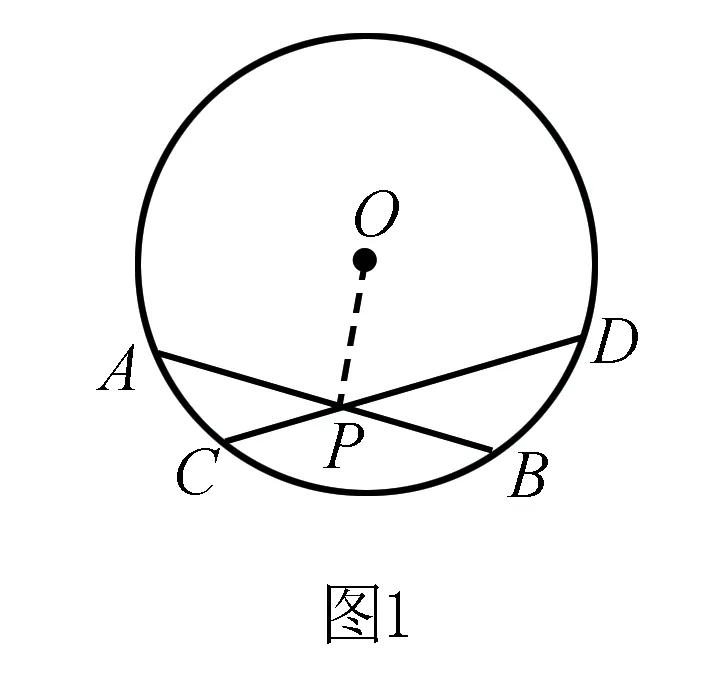
例1 如图1,AB、CD是⊙O的两条不过圆心的弦,并相交于点P.求证:AB与CD不能被点P平分.
证明 假设AB与CD被点P平分.连结OP,由垂径定理知OP⊥AB,OP⊥CD,因此AB∥CD.这与题目条件AB与CD相交矛盾.所以AB与CD不能被点P平分.
二、面积法
面积法就是通过面积之间的关系,将题型中需要证明的几何量进行表示,并且把题型在存在的几何量采用相关的图形面积体现.
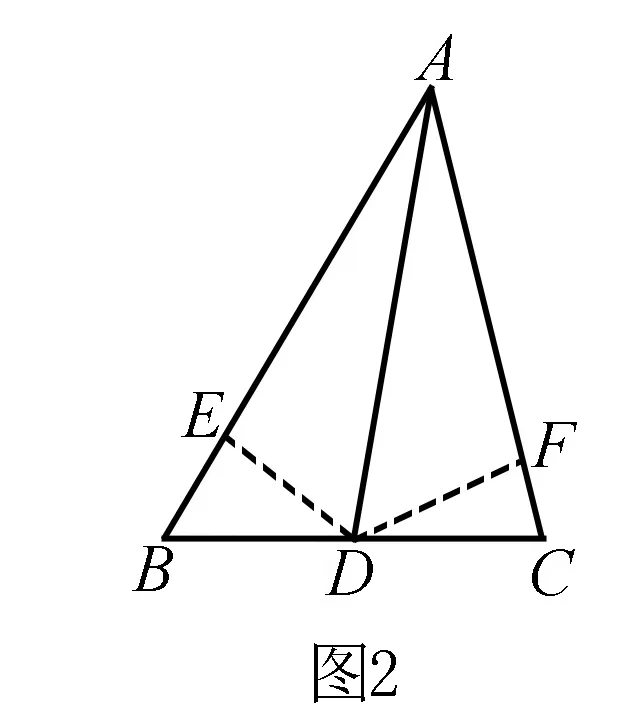
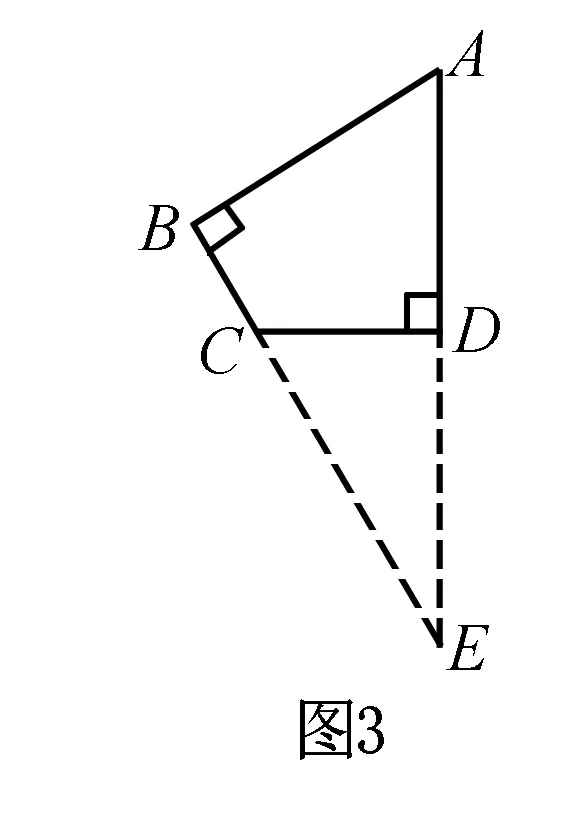
例2 如图2,△ABC中,AD是角平分线,求证:AB∶AC=BD∶DC.
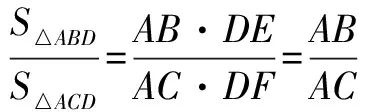
三、割补法
通过割补的方式,把比较陌生的形状转换成比较熟悉、比较常见的图形,进而进行解题.
例3 已知在四边形ABCD中,∠A=60°,∠B、∠D均为90°,∠C=120°,AB=2,CD=1,求BC、AD的长.
分析 延长BC、AD相交于E,可知∠E=30°,可求得AE,BE,CE,DE.
四、 分析综合法
按照原理去推导结果与按照结果去推导原因,这两种模式是学生在进行几何推理过程中比较常用的思维模式.前者它主要指的是,学生能够按照题目中给出来的已知条件,在解题的过程中,采用有关的定义或者是有关的公理进行推导,从而能将结论得出;而后者采用的是一种逆向的推理方式,也就是,在解题的过程中,从结果出发,将能够证明结论的条件找出.
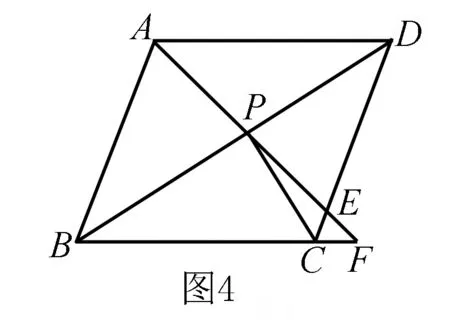
例4 如图4,在菱形ABCD中,点P是BD上的一点,将AP延长,和CD相交于E,和BS延长线相交于F.求证:PC2=PE·PF.
证明 求证PC2=PE·PF,一般情况下,都会将该式转变成比例式,也就是PC/PE=PF/PC;那么,只需要证明△FPC与△CPE相似.∠CPF为 公共角 . 因此,只需要证明:∠F=∠PAD 即可.根据已知条件中的菱形的性质知道:∠BDA=∠CDB,AD=CD,可得,△PAD全等于△PCD.所以∠PAD=∠PCD.又因为AD∥BF,可知∠PAD=∠F,所以∠PCD=∠F.
因此,PC2=PE·PF成立.
五、 几何变换法
初中阶段在学习的过程中,学生面对一些平面几何问题时,往往是束手无策,因为,这些题型中往往隐含的东西是比较分散的,不能轻易地被发觉,题型中的已知条件与结论隐藏得太深.对于这些情况,就需要学生们在解题中,能够巧妙地对图形进行相应的变换,把图形的某一个部位进行移位,或者是使其能够达成其他条件的要求,从而能够把几何的性质体现出来,进而实现分散条件的整合.只有掌握这些方法,学生在解题的过程中,才能有效地将题目的难度减少,那么学生的解题思路也会逐渐清晰.
总而言之,在初中阶段学习几何推理与图形证明,其主要的目的在于培养学生的空间感以及立体感与逻辑思维能力.因此,在进行问题解决的过程中,也需要通过空间感与立体感以及逻辑推理的应用解决问题.因此,教学过程中,老师需要把握好几何推理与图形证明的相应特点,从而能让学生掌握这些内容的知识点,从而能轻松地解题,从而能达到教学目标.
[1] 范成. 初中数学几何推理与图形证明策略例谈[J]. 数理化解题研究(初中版),2014(10)
[2] 沈定祥. 浅谈“基本图形”在初中数学几何教学证明中的作用[J]. 新课程学习(下),2014(06)
[3] 吕明. 初中数学“空间与图形”的入门教学[J]. 课程教材教学研究(中教研究),2013(Z5)
[4] 李珲. 打破题海战术的瓶颈,提升学生的解题能力[J]. 数理化解题研究,2016(11)
G
B
