分类讨论，建构“简单数学”教学课堂

甘肃省民勤县第三中学(733399)

刘发荣●



分类讨论，建构“简单数学”教学课堂

甘肃省民勤县第三中学(733399)

刘发荣●

在初中数学中有很多问题，经常需要进行分类讨论，从这些年中考题来看，用分类思想解题已经成为命题的热点.本文就分类讨论、建构“简单数学”教学课堂进行深入探究.

分类讨论；建构；简单数学；教学课堂

分类讨论思想方法是解决数学问题的一种重要的思想方法，它贯穿于整个初中数学教学中，是解决初中数学难题的不二法宝.因此，在课堂教学中，老师一定要注意培养学生的分类思想，使其构建一定的思维习惯，为将来的数学学习打好基础.

一、参数待定，速求实根

在初中数学学习过程中，经常会遇见题目中含有参数的题目，在解决这种类型的题目时，同学们一定要提高警惕，因为题干中所给出的参数是需要进行讨论的，在不同的习题中会有不同的分类讨论方法，需要学生能够自主去探究.与参数相关的题目有很多，老师不必要求同学们都逐一进行练习，在习题课中，老师可以课前挑选几个具有代表意义的问题与同学们分享，提高学生的分类讨论能力.例如，同学们都遇到过这样的题目：关于x的方程(m-4)x2-(2m-1)x+m=0，当m为何值时，方程有实根？首先我们一定要读懂题目，所谓方程有实根，就代表着它可能有一个或者两个实根，对应着一元一次方程和一元二次方程，因此我们需要对指数最高次项的系数进行分类讨论.第一种当m-4=0，即m=4时，原方程可以变为-7x+4=0，这时该方程就是一元一次方程，有且仅有一个实数根x=4/7.第二种情况就是m-4≠0，方程变为一元二次方程.我们还需要对Δ进行讨论.当Δ=-(2m-1)2-4(m-4)×m≥0，即m≥-1/12且m≠4时，方程存在两个实根.综合以上两种情况我们可以得出结论，当m≥-1/12时，原方程中存在实数根.这道题目就与参数相关，并且涉及到方程的知识，需要学生对各类基础知识都有一定的把握，能够清楚地认识到方程存在实根的真正含义才是解决此题的关键.很多同学看到x2就直接武断地认为该方程是一元二次的，这样的做法是错误的，需要同学们改正.

二、几何分析，妙求距离

初中几何也是中考的必考题目，老师在考试前也要为同学们总结几何题的解题方法.其中存在一类几何题目也是需要进行分类讨论的，老师可以列举几个相关的题目，强化学生对分类讨论的认识.

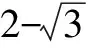
很多同学在读完题干之后.直接就想当然的认为A、B两点在直线a的同一侧，其实还存在二者在直线异侧的情况.

这道题目设置的目的就是要求同学们能够看到需要讨论的点，题目本身不难，难就难在能否看出同侧与异侧.

三、变量检验，因式化简

在很多题目中可能会存在多个变量，我们一定要考虑到各个变量间可能存在的关系，避免出现不必要的错误，因此需要我们对变量进行检验，在检验中抓准解题的关键.

由此可见，变量检验多么重要，一不小心就会丢分，希望同学们能够认真解题.

综上所述，分类讨论思想在各类题目中都有所体现，需要学生不断地去练习去熟悉.作为初中数学老师，在平时教学中一定要注重对学生思维方法的培养，只有掌握了解题的精髓才能够面临更多的挑战，使学生们在中考中取得佳绩.

[1] 张火木. 初中数学教学中数学思想方法的渗透[J].新课程学习(上)，2012(02).

[2] 李印. 初中数学中常见的分类讨论问题[J].数学教学通讯，2005(S3).

[3] 王志红. 探究分类讨论思想在初中数学教学解题中的应用[J].数学学习与研究，2014(18).

G

B