刍议初中数学“最值”问题的一些体会

江西省上饶市鄱阳县石门街中学(333100)

李晓华●



刍议初中数学“最值”问题的一些体会

江西省上饶市鄱阳县石门街中学(333100)

李晓华●

解“最值”问题，可将问题分成几类，然后有针对性地来解决.有以下几种方法来解决.

一、利用绝对值的概念来解决相关问题

例1 求|x+2|+|x-1|+|x-5|的最小值.

遇到这样的问题我们可以利用绝对值的定义来解决.

二、利用特殊不等式a2+b2≥2ab来解决

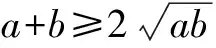
例如：要修建一个容积为8立方米，深为2米的长方体无盖的水池.如果水池底和水池壁的造价分别为每平方米120元和每平方米80 元，问此水池的最低造价是多少元？

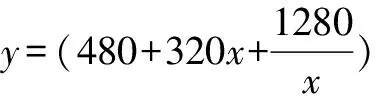
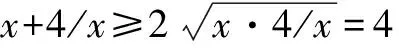
三、利用典型例题来解决几何中的最值问题

初中数学几何中，在讲到轴对称知识时，有这样的一个例题：如图，直线l的同侧有A和B两点,试在l上找一点P，使得PA+PB的和最小.

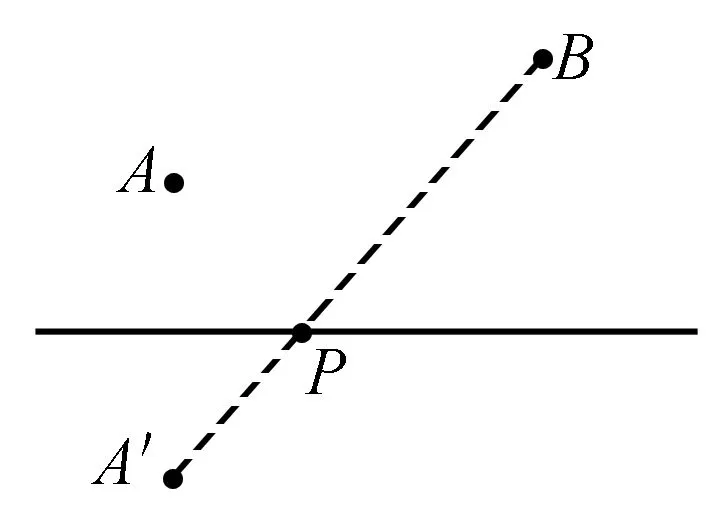
分析 通过学习，我们知道只要在l的另一侧找到A点的对称点A′，连接B和A′，与直线l的交点就是我们所找的P点.它是利用轴对称和三角形三边的相关知识来证明的.利用这个经典例题，进行适当的转化,我们可以解决许多类似的题目.

通过上述例题的研究，我们发现课本中的例题还是有比较好的利用价值的.我们在平时要善于思考总结.接着我们再来看此例题的延展.

四、利用某些线段的特殊性求解最小值

在直角三角形中，斜边上的中线等于斜边的一半.因此斜边上的中线是一条比较特殊的线段，利用这一特性，我们可以解决相关问题.

例如，如图，在平面直角坐标系中，以坐标原点O为圆心，3为半径画⊙O，P是⊙O上一动点，且P在第一象限内，过点P作⊙O的切线与x轴相交于点A点，与y轴相交于点B点.当点P在运动时，线段AB的长度在发生变化，请写出线段AB长度的最小值，并说明理由.

分析 本问题中,要求线段AB的最小值，而A、B点都随切线的改变而改变，不好直接求其最小值.而在Rt△OAB中，线段AB为斜边，取AB的中点C，连结OC，这样就利用直角三角形中，斜边上的中线等于斜边的一半得到OC=0.5AB，从而求出OC的最小值就可以解决斜边AB的最小值.又因为⊙O与边相切，连结O与切点P，所以半径OP⊥AB. 由图可以知，Rt△OAB中，斜边上的中线OC与斜边上的高OP重合时, 即OC=OP时，OC最短，此时AB也最短，得到 AB最小值为6.

当然，除了上面提到的几种类型外，还有像在几何问题中有时可用平面展开图的方法来解决距离最短问题等等.所以，解“最值”问题的方法多种多样，变化无穷的.

初中数学中的“最值”问题一直是一个让学生感到比较困难的课题，通过以上例题的探究，我们能感知到解此类问题还是有一定方法可循的.我们平时应多注意对知识的积累，遇到问题深入思考，养成良好的数学习惯，我们完全有能力学好数学.

G

B