受电弓导流板涵道式翼型气动补偿作用的数值模拟

庄林楠 王月明

(西南交通大学机械工程学院, 610031,成都∥第一作者，硕士研究生)



受电弓导流板涵道式翼型气动补偿作用的数值模拟

庄林楠 王月明

(西南交通大学机械工程学院, 610031,成都∥第一作者，硕士研究生)

利用Fluent软件对受电弓导流板涵道式翼形气动特性进行了二维数值研究,观察了不同涵道位置情况下导流板翼形周围流场的压力分布和速度分布,求出了各情况下导流板受到的升力及阻力,最后对受电弓稳定受流的气动补偿控制做出可行性预测。

受电弓; 导流板; 涵道式翼形; 气动补偿

Author′s address School of Mechanical Engineering, Southwest Jiaotong University, 610031,Chengdu,China

受电弓与接触网间的良好接触是保证电力机车高速运行时受电弓良好受流的基本条件。在列车高速运行时受电弓所受的空气阻力很大,不仅影响弓网间的良好接触,还增大了弓网磨损和气动噪声。若能实现受电弓主动补偿控制,则受电弓的气动特性就能有效地得到改善。使用导流板则是受电弓主动补偿控制方法中的一大有效措施。图1为受电弓导流板的示意图[1]。

探究导流板对受电弓高速受流和气动特性的影响,即是探究列车在高速运行时导流板产生的升力、阻力对受电弓接触压力的影响。由于导流板的横剖面可以视为翼型,所以对导流板升力、阻力的研究可以归结为对翼型升力、阻力的研究。

图1 导流板示意图

1 翼型介绍

1.1 翼型的几何定义

(1) 一般翼型最左边的点称为前缘,最右边的点称为后缘或者尾缘。对于低速翼型而言,其前缘较钝，呈类似圆弧的形状；而后缘往往是尖的。

(2) 前缘和后缘的连线称为弦线。弦线处于水平位置,因而可视为水平轴。弦线的长度称为弦长,一般由CA表示。

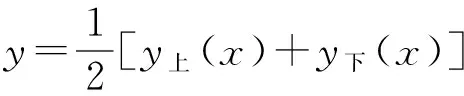
(4) 厚度与弯度。厚度分布函数的最大值即为厚度,而中弧线的最大高度与水平轴的间距即为弯度。

图2为翼型的几何参数示意图[2]。

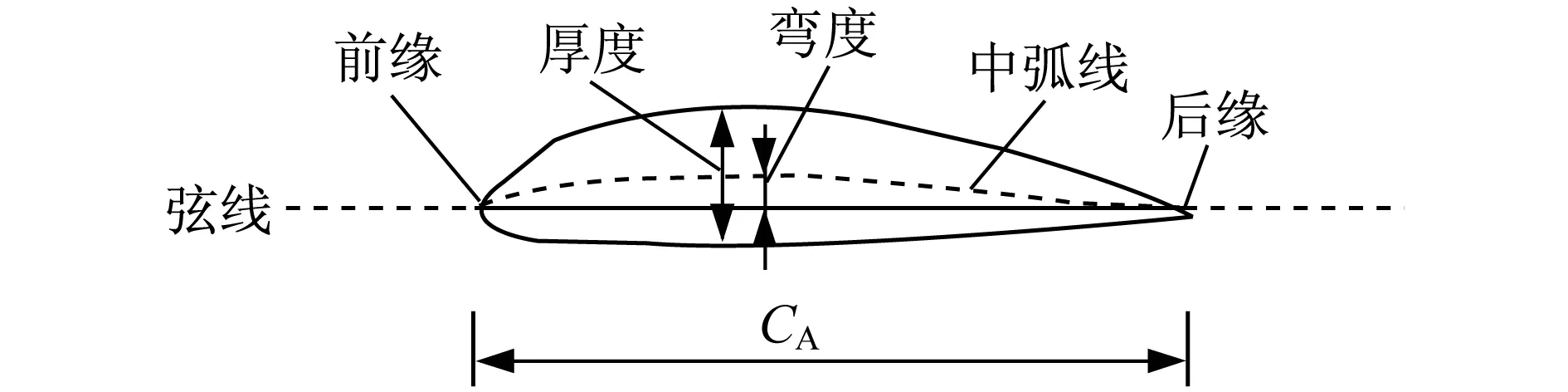
图2 翼型的几何参数示意图

1.2 翼型的气动参数

翼型的气动参数包括升力、阻力、升力系数、阻力系数、升阻比、力矩、力矩系数、压力中心及焦点等。气动力包括升力和阻力,还包含对力矩的分析。本文只对翼型受的升力、阻力及升力系数、阻力系数等进行着重分析与研究。

翼型在气流中受到的总的气动力R可分解为与来流垂直的升力L及与来流平行的阻力D(如图3所示)[2]。升力来自上下翼面的压力差,上翼面对于升力的贡献是向上作用的负压力(也就是吸力),下翼面对于升力的贡献则是向上抬的正压力。总的来说,上翼面的吸力比下翼面的压力大得多。阻力源于压力和摩擦力。L与D的比值称为升阻比。

图3 翼型气动力分解示意图

2 试验使用的翼型及涵道

为了探究上下、前后对称的特殊翼型在气流场中的空气动力学特性,为了实现翼型前后缘都能在流场中受升力影响而利用升力对受电弓导流板进行补偿控制,本次试验在E168翼型的基础上对翼型作出了一些改造,创造出上下、前后对称的翼型。翼型的最大厚度为12.2 mm,CA为123.4 mm。上下涵道搭载在列车车体上,可在上下移动涵道改变其垂向位置时使翼型产生较大的升力变化,进而寻求翼型升力最大时涵道的最佳垂向位置,以达到导流板最佳气动补偿的效果。涵道的长度是翼型CA的1.5倍,涵道的形状则是两端尖而中部平滑。图4所示为翼型平衡位(翼型上下表面与上下涵道间距相等,间距为12.5 mm)。

图4 翼型位于涵道中部(平衡位)时的示意图

3 模拟仿真

图4所示的平衡位是翼型上下表面距离上下涵道均为12.5 mm时的情况,而后将上下涵道视为整体,分别在其下移1、2、3 mm直至10 mm的不同情况下，采用Fluent软件对翼型进行仿真分析,得出各种情况下翼型所受的升力和阻力值。

3.1 网格划分及求解条件

由于翼型在涵道内上下移动,而建模和仿真计算是在翼型距离涵道上下表面不同距离的不同情况下分别进行,故以翼型处于平衡位的情况为例阐述网格划分的细节、边界条件及相关参数的选择。

本文采用的是结构化C型网格。考虑到流场内不同区域气流对翼型的作用不同,故采用分区域划分网格的方法。由于在翼型附近流动参数的梯度比较大,网格划分得密一些;流场外边界附近流动参数的梯度接近于0,网格划分得稀疏一些。总的来说，采用了自翼型向外渐疏的节点分布方式[3]。图5为流场网格示意图。

图5 流场网格划分图

流场的外边界采用速度入口,来流速度为0.245马赫。因流体速度较低,将流体视为不可压缩的黏性流体。紊流模型采用k-ε模型。松弛因子的设置如下:压力为0.3,密度、质量力和湍流粘性均为1,动量为0.7,湍动能为0.8,湍流耗散率为0.8。动量、湍流动能、湍流耗散率均选用二阶迎风格式。计算时监测翼型及上下涵道所受升力和阻力情况。

3.2 压力云图及速度云图

翼型在涵道中所处的位置不同时,对压力、速度分布及整个翼型附近风场分布的影响都各不相同。由图6和图7可知,翼型所受的风压峰值位置大多在前缘附近，故加工时所要加强的部位是前缘部分,即导流板的迎风面。风通过翼型时,其前缘部分压力值达到最大,从两侧逐渐减小[3]。由图8和图9可知,当涵道整体下移时,翼型上面的气流速度逐渐增大,计算区域内的速度最大值增大,翼型上下区域内气流的速度差也增大。

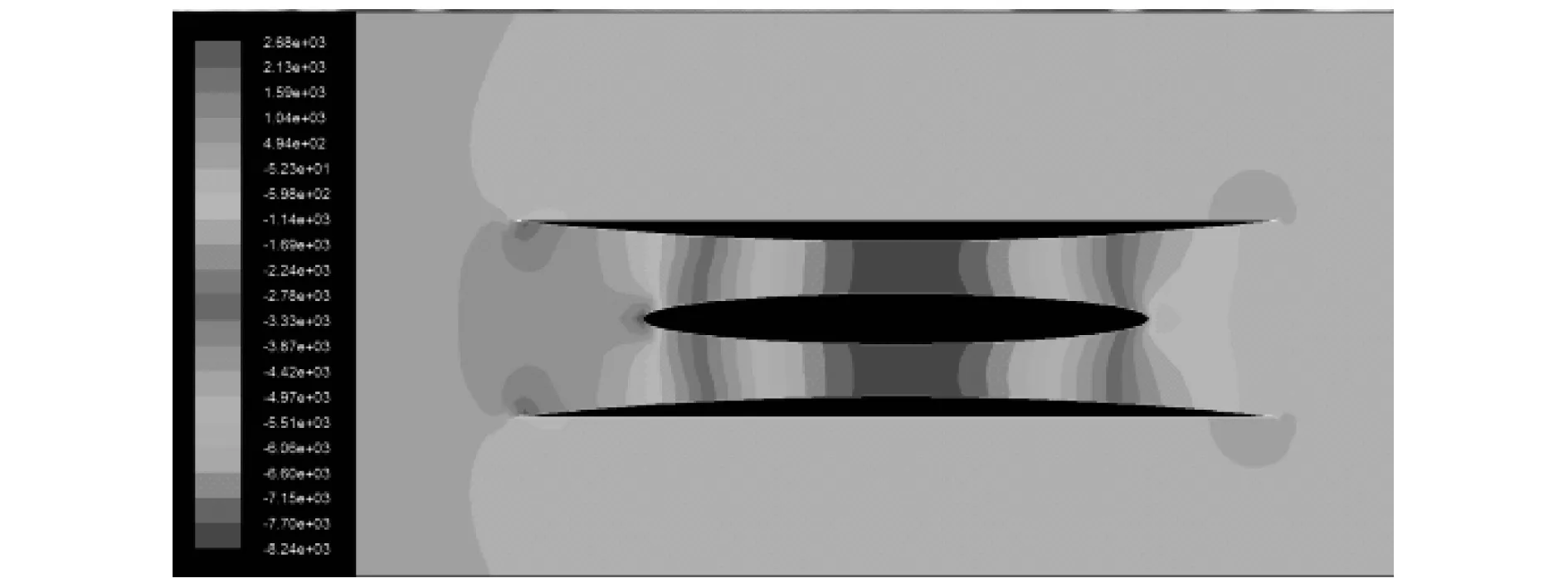
图6 平衡位时的压力分布云图

图7 涵道下移10 mm时的压力分布云图

图8 平衡位时的速度分布云图

图9 涵道下移10 mm时的速度分布云图

3.3 翼型的升力和阻力特性

随着翼型涵道相对位置的改变,翼型在气流场中所受的气流影响也发生改变,因而在涵道位置不同情况下翼型所受的升力和阻力也就不同。表1所示为涵道位置下移不同情况下,翼型所受的升力和阻力值。

由于在建模过程中对翼型和上下涵道没有设置重力,故竖直方向上不存在对涵道和翼型产生影响的力。所以,当把上下涵道作为一个整体上下移动相同距离时,上移和下移翼型所受的升力数值相等,方向相反;而阻力的数值保持不变,方向也同样与来流方向相反。因而可以,推断出当涵道整体上移时翼型所受的升力和阻力。当涵道下移时,翼型所受的升力方向向上,为正升力;而当涵道上移时,翼型所受升力方向向下,为负升力。涵道上移位置不同时翼型升力、阻力,数值如表2所示。

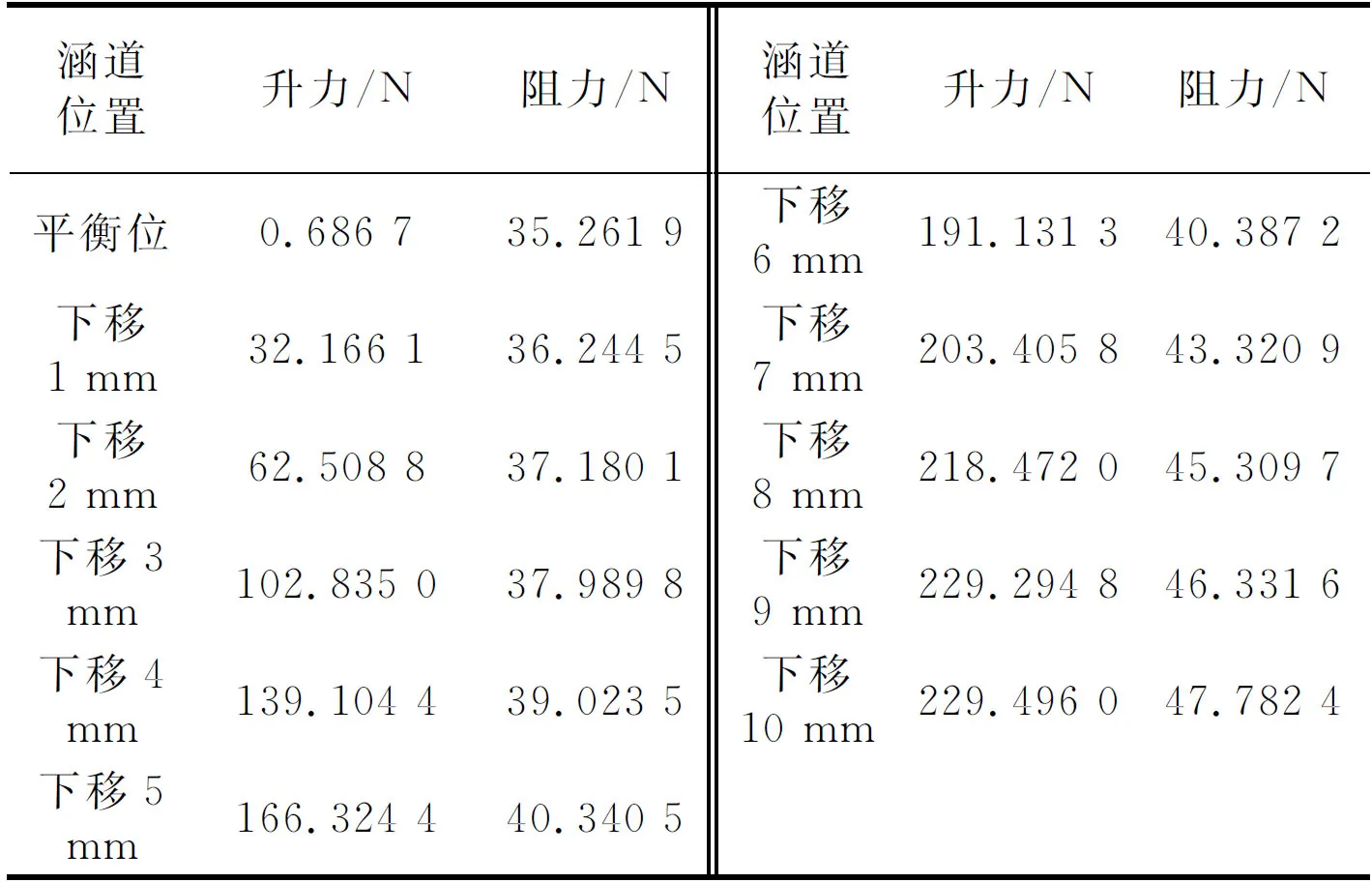
表1 涵道下移时翼型的升力和阻力值

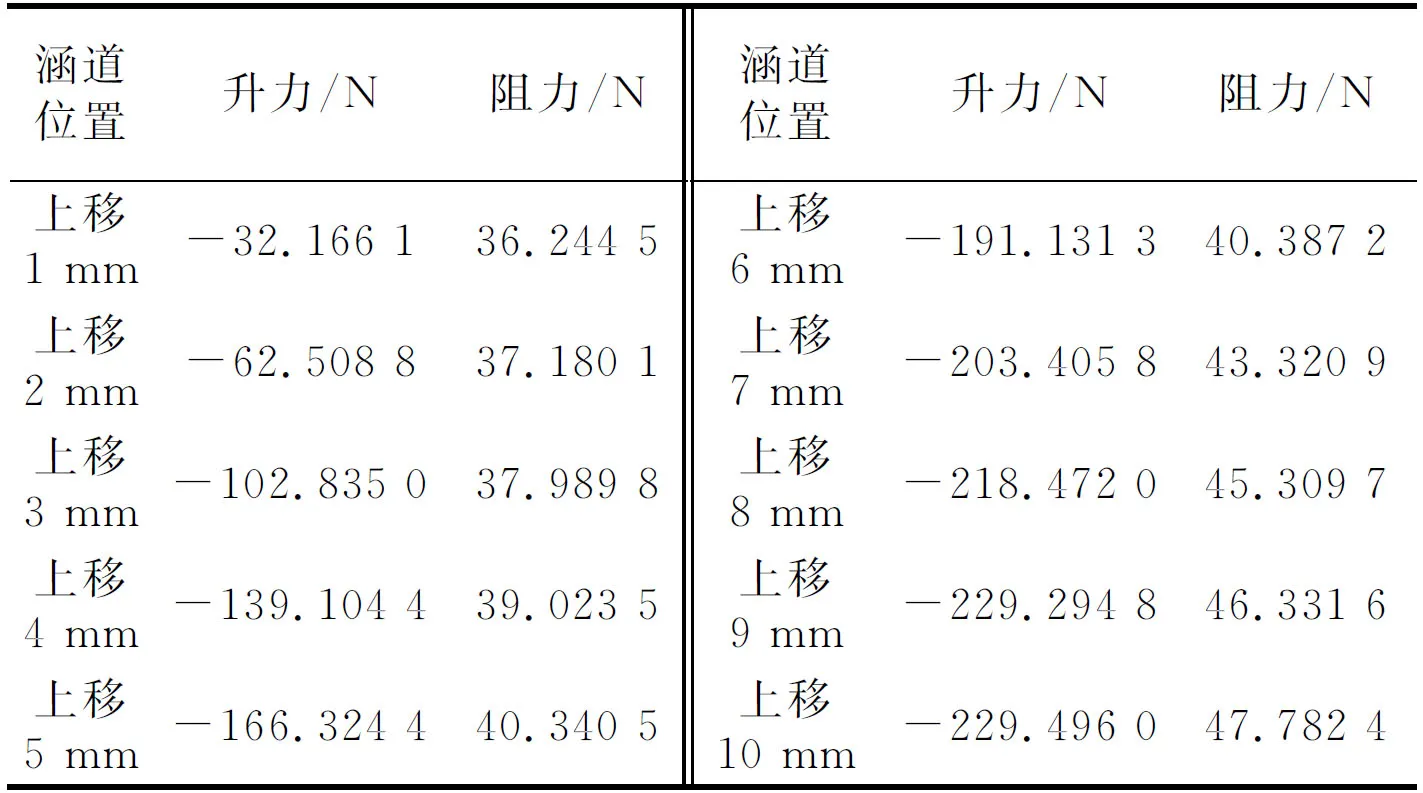
表2 涵道上移时翼型的升力和阻力值

由表1和表2的数据可以得出翼型在涵道中不同位置时所受的升力、阻力的变化曲线图,如图10所示(其中翼型处于平衡位的情况是处于坐标原点,而涵道下移时记为正,为X轴的正半轴;涵道上移时记为负,为X轴的负半轴)。

图10 翼型升力、阻力变化曲线

由升力、阻力变化曲线可以看出翼型在涵道内升力变化是远大于其气动阻力的,而且涵道位置较小的变化也能使翼型所受升力产生较大变化。升力的变化幅度较大且随着远离平衡位逐渐放缓。在一定范围内可通过改变涵道的垂直位置改变导流板的气动升力，进而改变弓网间接触力,为受电弓稳定受流提供良好的条件。

3.4 导流板气动补偿作用分析

由前述的数值模拟结果及升力、阻力曲线可以看出,通过控制涵道与翼型的垂向相对位置可以提供-200～200 N的气动升力,且在该区段内升力呈近似的线性变化。

列车运行速度为300～350 km/h时,当TSG19型受电弓处于开口状态时,受电弓产生的气动升力大约为90～130 N;闭口时产生的升力约为50～60 N(如图11所示)[1]。涵道式导流板翼型能提供多达200 N的气动补偿力,所以通过改变涵道的垂向位置以使导流板产生气动升力，进而对受电弓受流进行主动控制的可行性较大。

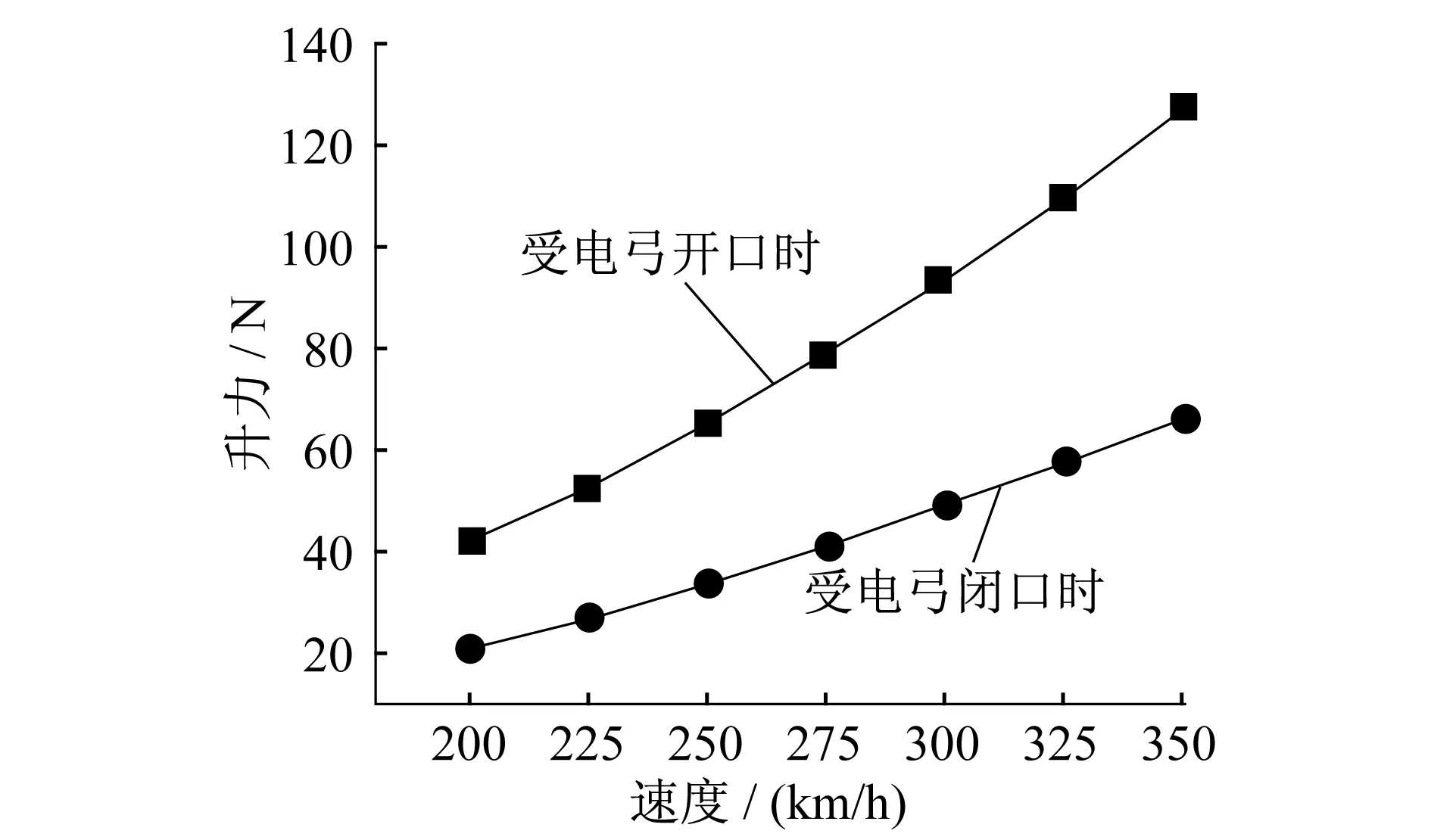
图11 TSG19型受电弓的气动抬升力

4 结语

本文在受电弓导流板翼型E168的基础上对翼型进行改良。结合车载涵道,利用Fluent软件对涵道式翼型进行建模、仿真分析,观察不同涵道位置情况下翼型周围的风场情况,包括压力分布速度分布等,并从中获得翼型在各情况下的升力和阻力值,为导流板应用于改善受电弓受流稳定提供可行性研究。分析表明:在改变涵道位置时,导流板横截面翼型能产生有效的气动升力,同时保证气动阻力变化不大,而且相比于升力,气动阻力造成的影响很小。可为受电弓与接触网的良好接触提供可靠控制,从而改善受电弓气动特性,满足高速受流要求。

[1] 欧阳鹏,柳萍,王月明,等.受电弓导流板气动特性的二维数值研究[J].电力机车与城轨车辆,2010,33(6):17.

[2] 吴子牛.空气动力学(上册)[M].北京:清华大学出版社,2007.

[3] 韩占忠.FLUENT流体工程仿真计算实例与分析[M].北京:北京理工大学出版社,2009.

[4] 王福军.计算流体动力学分析:CFD软件原理与应用[M].北京:清华大学出版社,2005.

[5] 于勇.FLUENT入门与进阶教程[M].北京:北京理工大学出版社,2008.

[6] 徐华舫.空气动力学基础(上册)[M].北京:北京航空学院出版社,1986.

Numerical Simulation on Aerodynamic Air Supply of the Pantograph Culvert Airfoil

ZHUANG Linnan, WANG Yueming

Fluent software is used for the study of 2-D numerical simulation on the aerodynamic characteristic of culvert airfoil, the static pressure and speed distributions of the airflow field surrounding the airfoil under different vertical positions of culvert are monitored. Then the lift force and drag force acting upon the air deflector in each position is calculated, the result leads to a feasibility prediction on the aerodynamic air supply control of pantograph’s air deflector in order to ensure the stable power-receiving.

pantograph; air deflector; culvert airfoil; aerodynamic air supply

TM 922.6

10.16037/j.1007-869x.2016.06.018

2014-09-22)