基于AnyLogic仿真的城市轨道交通枢纽通道宽度研究*

聂广渊 袁振洲 吴昊灵

(1.铁道第三勘察设计院集团有限公司，300142，天津；2.北京交通大学交通运输学院,100044,北京∥第一作者，助理工程师)



基于AnyLogic仿真的城市轨道交通枢纽通道宽度研究*

聂广渊1袁振洲2吴昊灵2

(1.铁道第三勘察设计院集团有限公司，300142，天津；2.北京交通大学交通运输学院,100044,北京∥第一作者，助理工程师)

选取北京城市轨道交通枢纽西直门站单双向客流条件下的步行通道进行调研,采集乘客步行速度,统计得到85%行人步速分布区间。基于AnyLogic软件构建客流交通模型,利用调研数据标定仿真参数。在仿真过程中通过改变通道宽度及客流量,输出通道内的区域密度数据,拟合宽度-密度函数曲线并建立函数模型。最终给出不同客流量条件下的通道宽度建议取值。

城市轨道交通枢纽; 步行通道; 通行能力; 服务水平

First-author′s address The Third Railway Survey and Design Institute Group Corporation,300142,Tianjin,China

城市轨道交通枢纽常存在的步行通道较窄及通道内客流双向混行现象,会导致乘客走行速度受限,且拥挤和排队现象严重,严重影响通道的通行能力和服务水平。通道的通行能力是指在特定条件下,单位时间内通过通道某一断面的行人最大流量。在轨道交通枢纽和轨道交通车站内,步行通道的通行能力受行人步行速度、客流密度、通道有效宽度等因素影响。其中，最主要的影响因素是通道的有效宽度。

国内外对于轨道交通步行通道的研究主要集中在通道内行人交通特性和通道优化设计上。文献[1-4]对广州、上海、南京等城市轨道交通车站的通道、楼梯、自动扶梯等设施进行了实地调查,对各设施处的行人交通特性进行研究,建立行人流量-密度及速度-密度关系模型、路阻函数模型,为轨道交通车站内设施布局优化提供理论依据。文献[5]构建了平均步距最短的通道优化设计目标函数,并针对步行通道的瓶颈提出改善建议。文献[6]构建了排队优化模型,将行人服务水平的概念引入到地铁人行通道通行能力的计算中。文献[7]考虑了通道服务水平的因素,调查并分析了客流特性,通过构建仿真系统对单向客流条件下的通道宽度进行了探讨。文献[8]利用VISSIM构建客流交通模型,并进行了模型的校正和检验,对高强度客流下的世博会进出口通道进行了仿真分析。以上文献在对地铁通道宽度进行研究时,并未同时考虑单、双向客流条件及服务水平分级,文献[9]中对于通道最大通行能力及宽度取值也未考虑服务水平因素。本文基于步行通道服务水平分级标准及AnyLogic仿真模型,对轨道交通枢纽单双向通道宽度取值问题进行研究。

1 行人仿真模型及相关软件

根据仿真模型对行人系统细节描述程度的不同,行人运动仿真模型可分为宏观、中观、微观模型三种。宏观模型主要包括行人动力学模型和空间交互熵最大化模型,一般把多个行人作为一个整体,不考虑单个行人的行为,不仅无法刻画瓶颈处的动态变化,也难以表示行人与行人之间的相互作用[10]。

中观模型既保留了宏观模型中的流量、速度、密度等特性数据,也保留了微观模型中的核心数据。这种模型将行人流描述为若干行人个体构成的队列单元,能描述节点处的动态变化,但不能细致地描述行人个体之间的相互作用,其代表性的模型为格子气模型[11]。

微观模型可研究个体的运动行为,并能表示人与人、人与环境之间的相互作用。由于行人的特性均表现在微观层面,所以微观模型在描述行人之间、行人与周边环境的相互作用方面具有很大优势。高速发展的计算机技术,使更加复杂的模型得以运用[12]。其代表性的模型有元胞自动机模型、磁力场模型、社会力模型等。

常用的行人交通仿真软件有Legion、Steps、AnyLogic、SimWalk、SimPed、Vissim等。其中，AnyLogic软件的行人仿真主要依靠其行人库完成,能输出行人数目、平均密度、停留时间等数据。AnyLogic的核心算法是社会力模型。该模型认为行人共受到驱动力、人与人之间的作用力、人与边界之间的作用力三种力,能较好地反映行人的自组织特性。其行人走行轨迹方向性明显,且在最短路径或最佳路线附近摆动。社会力模型用数学解析方法表达了行人在复杂环境下的运动过程,由于该模型的连续性特征使其可以精确描述各种层次的作用力,故模型计算结果可靠,比较接近真实情况[13]。基于以上优点,选用AnyLogic软件进行仿真分析。

2 行人步行速度调查与分析

选取北京城市轨道交通枢纽西直门站的两条地下水平步行通道进行数据调查,数据采集时段为早高峰(7:00—9:00)。2条通道中，一条为单向客流通道,另一条为双向客流通道(高峰小时主次方向客流比例为5∶1)。获取城市轨道交通枢纽通道内的行人步速分布,作为标定仿真模型参数的依据。

2.1 单向通道

为避免使用某一具体的数值来描述乘客步速而引起争议,故采用调研数据里85%乘客步速所在区间来分析乘客特征。调研样本为 484 人,有效样本为 462 人,乘客步速分布如图1所示。利用SPSS软件进行 K-S 检验,在单向客流通道内的乘客步速服从泊松分布,乘客步速分布在[0.6, 1.5]m/s区间。

图1 单向通道乘客步速直方图

2.2 双向通道

同样采用了调研数据中85%乘客速度所在区间分析乘客特征,调研样本为 477 人,有效样本为 452 人,乘客步速分布如图2所示。利用SPSS软件进行K-S检验,在双向通道内的乘客步速服从泊松分布,乘客步速分布在[0.5, 1.4]m/s区间。

图2 双向通道乘客步速直方图

3 AnyLogic仿真思路及参数设置

3.1 仿真思路及模型构建

首先，针对通道宽度及单双向客流,利用北京西直门城市轨道交通枢纽调查结果标定仿真参数；然后，在单向客流及双向客流 (5∶1)条件下,通过改变小时客流量及通道的宽度来统计区域行人密度,并拟合通道宽度-密度函数曲线；最后，建立函数模型并进行分析,基于服务水平给出不同客流量下的通道建议宽度。构建的仿真模型及场景见图3。

图3 仿真整体布局图

3.2 仿真参数设置

在系统仿真建模之前,根据研究目的,对系统进行一定的假设和说明以简化模型,从而降低仿真模型建立的难度和减少无关因素的干扰。

(1)简化行人的占地形态,将乘客的占地空间简化为二维圆形。

(2)简化行人的走行模式,设定行人受其他行人、墙壁、障碍物的综合作用力,且均以最短路径走行至各自的目的地,无需向他人问路,无折返等现象。

(3)根据西直门站实际客流调查结果,采用85%乘客步速分布区间,设定单向客流的乘客走行速度为[0.6, 1.5]m/s,双向混行客流 (5∶1) 的乘客走行速度为[0.5, 1.4]m/s。

(4)根据行人空间需求相关理论,设定墙壁接触容差为0.3 m。早晚高峰乘客以不携带任何物品及携带小包乘客为主,设定行人占地空间直径为[0.4, 0.6]m[14]。

(5)早晚高峰客流以单独出行上班的青年人群为主,客流结构设置为个人而非组团。

3.3 仿真模型的校验

模型校验的目标是通过调整影响仿真模型的参数,使得多个参数综合作用后模型输出的统计数据及反映的交通运行状态与实际情况相近[8]。如果不相符,需要对参数进行校准,调整参数取值范围,重新仿真校验,直到仿真结果符合实际结果为止。3.2节中给出的参数均已经过校验,由表1中仿真密度与实测密度的结果对比可以看出,仿真模型比较符合实际,可进一步用于仿真分析。

4 基于AnyLogic仿真的通道宽度取值

4.1 单向通道宽度取值

模拟环境为城市轨道交通枢纽单向步行通道，模拟工况采用2 000、4 000、6 000、8 000、10 000、12 000 人次/h 等6种客流量及2、3、4、5、6、7、8 m等7种通道宽度，共42种组合。利用AnyLogic软件，分别模拟42种工况的客流状况,并在系统运行1 000 s 后开始采集数据,每5 s 输出一次数据,每种工况收集1 000组通道内区域密度值。通过计算得到区域平均密度后，可拟合单向通道宽度-密度曲线 (见图4) 并建立函数关系 (见表2)。

表1 实测密度与仿真密度对比

图4 单向通道宽度-密度拟合曲线图

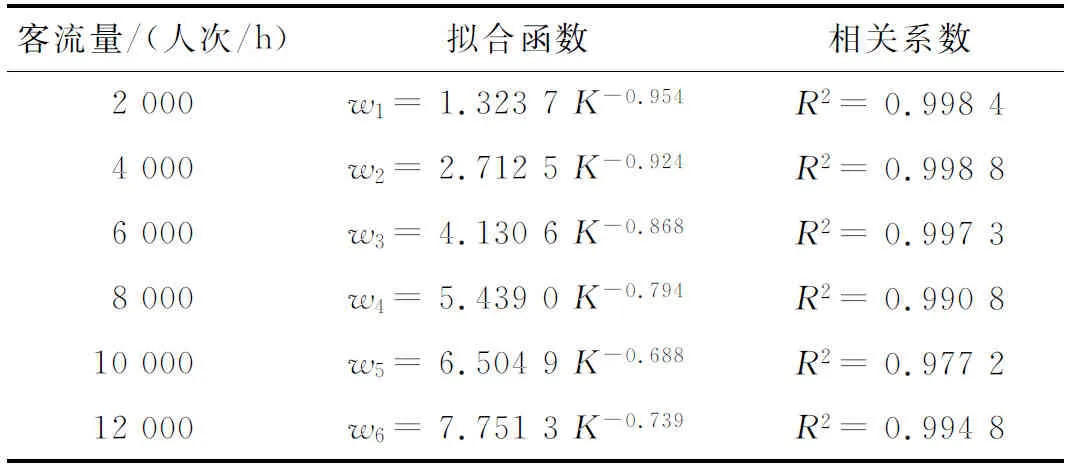
表2 单向通道函数模型表

考察拟合结果(表2)发现,幂函数的总体拟合效果较好,其函数模型为:

W单=aKb

(1)

式中：

W单——通道宽度(单向客流)；

K——密度；

a、b——模型参数。

参照《美国公共交通通行能力和服务质量手册(II)》[15]中规定的步行通道服务水平分级标准(见表3),以区域密度为服务水平主要分级依据,利用拟合函数模型计算得到不同客流量、不同服务水平下的单向步行通道的建议宽度(见表4)。

4.2 双向通道宽度取值

在双向混行客流 (5∶1) 条件下模拟城市轨道交通枢纽地下水平通道内的客流状况,其数据采集方法与单向水平通道相同。模拟工况分别为2 000、4 000、6 000、8 000、10 000人次/h等5种客流率及3、4、5、6、7 m等5种宽度，共25种组合。每种工况收集1 000组通道内区域密度数据,并统计得到双向混行客流条件下的区域密度值。利用获得的数据拟合双向混行通道宽度-密度曲线 (见图5), 并建立函数关系(见表5)。

表3 步行通道的服务水平分级

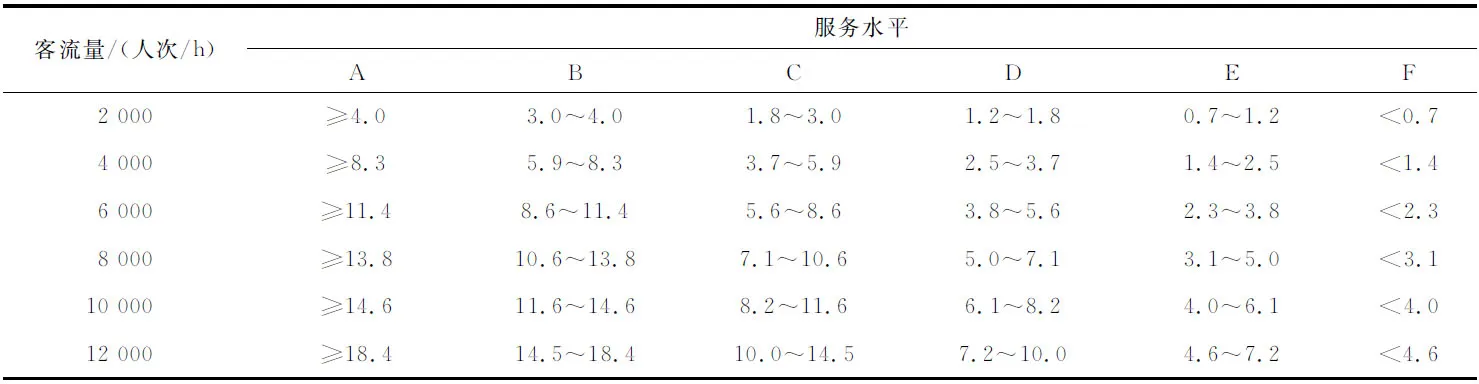
表4 不同客流量及服务水平的单向通道建议宽度 m

图5 双向通道宽度-密度拟合曲线图

表5 双向通道函数模型表

考察拟合结果(表5)发现,幂函数的拟合效果较好,其函数模型为:

W双=aKb

(2)

式中：

W双——双向混行步行通道宽度。

同样根据文献[15]中规定的步行通道服务水平分级标准 (见表3), 利用拟合的函数模型计算得到不同客流量、不同服务水平条件下双向步行通道的建议宽度 (见表6)。

4.3 分析与建议

以往通道宽度的经验公式[7]:

(3)

式中:

B——通道宽度,m;

Q——超高峰客流量,为已知量,人次/h;

α——不均匀系数,一般取1～1.25;

C——单位宽度的最大通行能力, 视服务等级而定,人次/(h·m)。

《地铁设计规范》规定的单向1 m宽通道的最大通行能力为5 000人次/h,双向1 m宽通道的最大通行能力为4 000人次/h。利用式(1)及规范中规定的最大通行能力,在超高峰系数和不均匀系数均取1.2的情况下,可计算得到不同客流量条件下的单双向通道宽度规范值。

将规范计算值与仿真得到的建议值对比 (见表7) 发现,采用规范值的通道基本处于F级服务水平状态,即依规范值设计的通道宽度偏窄,其通行能力不能完全满足乘客需求,服务水平偏低,在实际运营时易发生拥堵。在E级服务水平状态下，通道饱和度 (单位宽度的行人流量与单位宽度的最大通过能力之比) 为 0.8～1.0, 相应的设施通行能力基本能够满足乘客通行需求,且节约成本。故建议采用建议值对轨道交通枢纽步行通道进行设计,使之尽可能达到E级服务水平,如有条件也可按照D级服务水平进行设计。

表6 不同客流量及服务水平的双向通道建议宽度 m

表7 地铁通道宽度规范值与仿真建议值的对比 m

5 结语

本文基于AnyLogic仿真软件,利用北京西直门轨道交通枢纽实地调查数据标定仿真参数,利用仿真结果拟合步行通道宽度-密度关系曲线,发现通道宽度-密度关系符合幂函数模型。基于步行通道服务水平分级标准给出单、双向通道宽度的建议取值,与《地铁设计规范》对比发现,按规范设计的通道宽度取值偏低,且多处于F级服务水平状态。研究结果可为不同客流量条件下轨道交通枢纽的步行通道设计提供参考。研究方法同样适用于轨道交通车站、大型建筑内的步行通道宽度研究。

[1] 翁小雄,曾红艳.地铁内通道交通性能实例分析[J].中国安全科学学报,2011,21(5):109.

[2] 张晓军,张宁,陈晖.城市轨道交通行人通道路阻函数拟合[J].城市轨道交通研究,2011(1):33.

[3] YE Jianhong,CHEN Xiaohong,YANG Chao,et al.Walking behavior and pedestrian flow characteristics for different types of walking facilities[J].Transportation Research Record,2008(2048):43.

[4] CHEN Xiaohong,YE Jianhong,JIAN Nanjing.Relationships and characteristics of pedestrian traffic flow in confined passageways[J].Transportation Research Record,2010(2198):32.

[5] 王磊,杨晓光,陈春等.地铁站乘客步行通道的优化设计[J].城市轨道交通研究,2003(2):41.

[6] 蒋阳升,胡路,卢果.基于排队论的地铁人行通道宽度取值方法[J].交通运输工程学报,2010,10(3):67.

[7] 南海超,胡路,王文谨,等.地铁车站客流服务水平与通道宽度关系的探索[J].铁道勘察,2009,35(2):109.

[8] 孙剑,董斌杰,李克平.VISSIM 在世博高强度客流设施服务水平分析中的应用[J].城市轨道交通研究,2008(10):23.

[9] 中华人民共和国国际质量监督检验检疫总局,中华人民共和国住房和城乡建设部.地铁设计规范:GB 50157—2013[S].北京:中国建筑工业出版社,2013.

[10] 郭谨一,刘爽,陈绍宽,等.行人运动仿真研究综述[J].系统仿真学报,2008,20(9):2237.

[11] 胡明伟,史其信.行人交通仿真模型与相关软件的对比分析[J].交通信息与安全,2009,27(4):122.

[12] 韩冬,张蕊.行人微观仿真中的运动模型与行为模型——STEPS与NOMAD模型对比[J].城市交通,2008,6(6):33.

[13] 孙剑,李克平.行人运动建模及仿真研究综述[J].计算机仿真,2008,25(12):12.

[14] 曹守华.城市轨道交通乘客交通特性分析及建模[D].北京:北京交通大学,2009.

[15] Transportation Research Board.Transit Capacity and Quality of Service Manual—2nd Edition[R].Washington DC:Transportation Research Board,2005.

Research on Passageway Width at Urban Rail Transit Hub Based on AnyLogic Simulation

NIE Guangyuan, YUAN Zhenzhou, WU Haoling

Xizhimen rail transit hub in Beijing is selected as the research target to study the passageway width, which is the main factor influencing the transport capacity. The data of pedestrian walking speed, including the one-direction way and bi-direction way is collected, covering a range of 85% pedestrian walking areas. Based on AnyLogic simulation software and survey data, the simulation parameters are calibrated. By changing the passageway width and the passenger flow in the process of simulation, outputting the regional density data, fitting the width-density function curve, a functional model is established. Finally, the passageway width at rail transit hub according to different service levels and different pedestrian flows is suggested.

urban rail transit hub; passageway; transport capacity; service level

*国家重点基础研究发展计划项目(2012CB725403)

TU 921

10.16037/j.1007-869x.2016.06.007

2015-08-18)