基于模拟退火-粒子群算法的wMPS布局优化

岳翀，熊芝,1b，薛彬

(1.湖北工业大学a.机械工程学院；b.现代制造质量工程重点实验室，武汉430068；2.天津大学海洋科学与技术学院，天津300072)

基于模拟退火-粒子群算法的wMPS布局优化

岳翀1a，熊芝1a,1b，薛彬2

(1.湖北工业大学a.机械工程学院；b.现代制造质量工程重点实验室，武汉430068；2.天津大学海洋科学与技术学院，天津300072)

空间测量定位系统是一种在多测站协同作用下实现坐标测量的大尺寸测量系统，因此测站布局优化成为了重要研究问题。为解决此问题，本文提出了一种基于模拟退火粒子群算法的测站优化部署方案，以定位精度，覆盖度，使用成本作为优化函数，运用粒子群算法及模拟退火算法进行协同搜索，并建立模拟退火粒子群算法的测站布局优化流程，对两到四个测站进行仿真优化分析。仿真结果表明，该方法能快速收敛于最优解并获得一种较优的测站布局。

大尺寸测量；测站部署；空间测量定位系统；模拟退火粒子群算法

0 引言

空间测量定位系统(workspace Measuring and Positioning System,wMPS)是一种新型的网络式多站测量系统，随着测站数的增加，系统的测量范围将会拓展，同时测量成本也将增加[1]。此外，测站的不同布局也会导致系统定位精度的显著差别。研究测站布局对系统定位精度的影响能为提高系统覆盖范围，降低成本提供依据，因此成为wMPS系统设计的一个基本问题[2-4]。

在测站布局研究方面，德国亚琛工业大学机床与制造工程研究所的Robert Schmitthe等人[5]对该系统在机器人定位跟踪时的几种典型布局进行了仿真分析，考虑了时间t的测量误差和0.1 mm的发射站系统误差，并和激光跟踪仪的测量结果对比，结果表明标准型的测量效果最好。文献[6]中作者从wMPS网络布局和定位误差关系入手，研究了典型布局对定位误差的影响，实验结果表明O_4型布局整体测量精度最高。以上对测站网络布局的研究均是对特定布局进行了研究与对比实验，当测量环境变得复杂时缺乏灵活性与通用性。近年来，随着计算机技术的发展，智能算法逐渐成为解决网络测站优化布局最受欢迎的手段之一，文献[7-8]运用遗传算法从wMPS发射站光平面在测量点的不同交汇方式对测量稳定性的影响入手，建立数学模型，以此来评价布局的优劣，仿真结果表明四站系统的测量稳定性优于三站和两站系统。但由于遗传算法中交叉和变异概率固定易造成早熟现象，常常收敛不到最优解。

因此本文从wMPS测站网络布局与定位精度，覆盖度及使用成本的关系入手，设计了一种基于模拟退火-粒子群算法的wMPS测站优化部署方法，运用粒子群算法的快速收敛性及模拟退火算法的全局收敛性进行协同作用，对两到四个随机测站布局组成的网络布局进行仿真研究，结果表明，本文提出的方法能快速收敛于最优解并获得一种较优的测站布局。

1 wMPS系统中多目标优化问题基本描述

1.1测量原理

wMPS组网测量模型如图1所示，主要包括发射站，接收器，解算工作站。当系统工作时，发射站发射两束旋转激光平面，接收器接收光信号后，将光平面产生的脉冲转化为相对应的时间信号，并发送给解算工作站。解算工作站通过解算多个测站时间信号从而获得空间点的三维坐标值[9-11]。

1.2 目标函数

1.2.1 定位精度分析

本文采用作者先前工作所得到的定位精度模型[6]，由于定位精度与下文提及的覆盖度，使用成本分属不同量纲，因此需将其进行归一化。定义空间上任意一点P的归一化精度表达式：

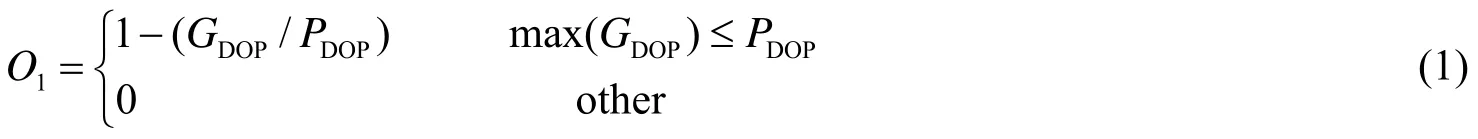
其中：PDOP为用户提出的测量精度，GDOP为精度几何稀释因子。

1.2.2 覆盖度分析

图2为wMPS单向通讯模型，Rmin和Rmax是发射站的有效工作距离，图中阴影部分为测站的有效工作距离。

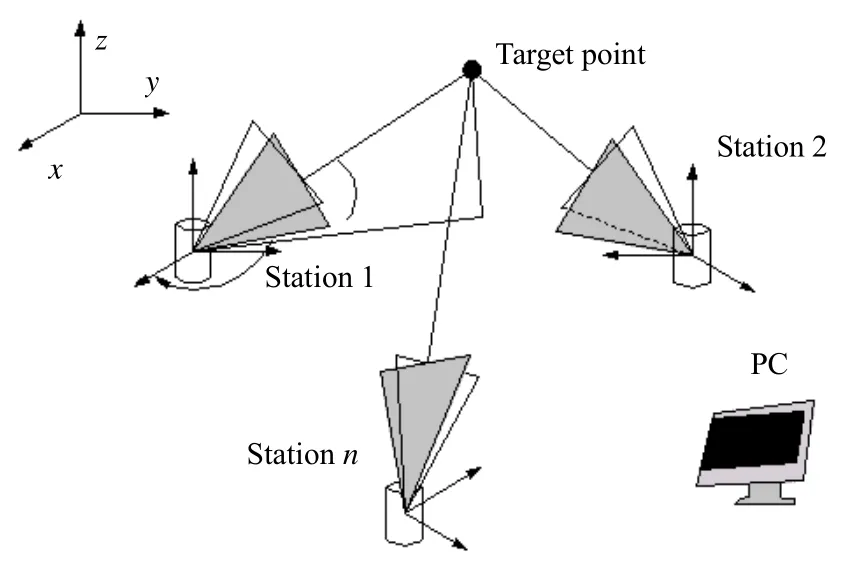
图1 wMPS组网测量模型Fig.1Networking measurement model of wMPS

图2 wMPS单站通讯模型Fig.2Constraint model of wMPS direction communication

在wMPS中，当空间有2个及以上测站时，即可通过角度交汇实现坐标测量，则对于有一定高度的平面区域，此时测站的覆盖度为

式中：d(Pi,Tj)为被测目标Pi与任意测站Tj之间的欧式距离，β为垂直角，φmax为测站光平面最大倾角，N为测站个数。文中将测站的覆盖度问题定义为当前布局覆盖被测点的个数Nnum与总被测点个数Ntol之比。

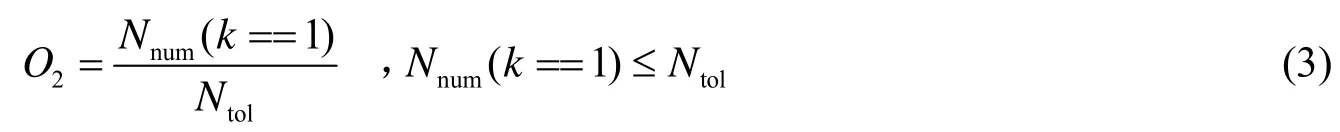
1.2.3 使用成本分析

仅考虑测站完成测量任务时的投资成本。在所有测站都被部署完毕后，则每种布局下测站的成本消耗：

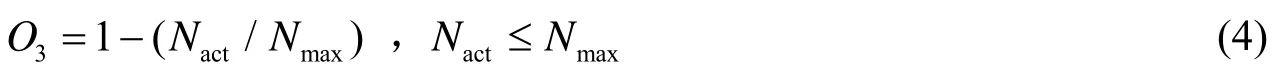
其中：Nact是实际使用的测站数，Nmax是可使用的测站数。

1.2.4 目标函数的定义

基于上述目标函数的分析，给每个目标赋予一定的权重，则wMPS布局优化函数为

式中：Ki(i=1,2,…,n)为权重，且值代表了被测点在此种布局下的适应度值的大小，本文优化的目的就是在给定的测量区域下获得一种f值较高的空间任意布局。

2 优化算法设计

2.1 模拟退火-粒子群算法

粒子群算法(Particle Swarm Optimization,PSO)是一种基于群体的随机优化方法，其思想是将每个可能的解表示为种群中的粒子，每个粒子均有自己的速度和位置，并有一个由目标函数决定的适应度。所有粒子在搜索空间内以一定速度飞行，通过追随当前最优值来寻找全局最优[12]。粒子群算法在早期收敛速度较快，但易受参数选取和优化目标函数性质等问题的影响，导致算法中后期收敛速度慢，易陷入局部最优。

为解决粒子群算法易陷入局部最优的问题，本文设计了一种将模拟退火算法(SimulatedAnnealing,SA)与粒子群算法相结合的模拟退火粒子群算法[13]，将模拟退火思想引入至粒子的速度和位置更新过程，采用Metropolis接受准则[14]，持续进行“产生新解—判断—接受或舍弃”，使得算法能从局部最优值中跳出，自适应调整退火温度，从而收敛至全局最优解。

2.2 基于模拟退火-粒子群的wMPS测站布局优化流程

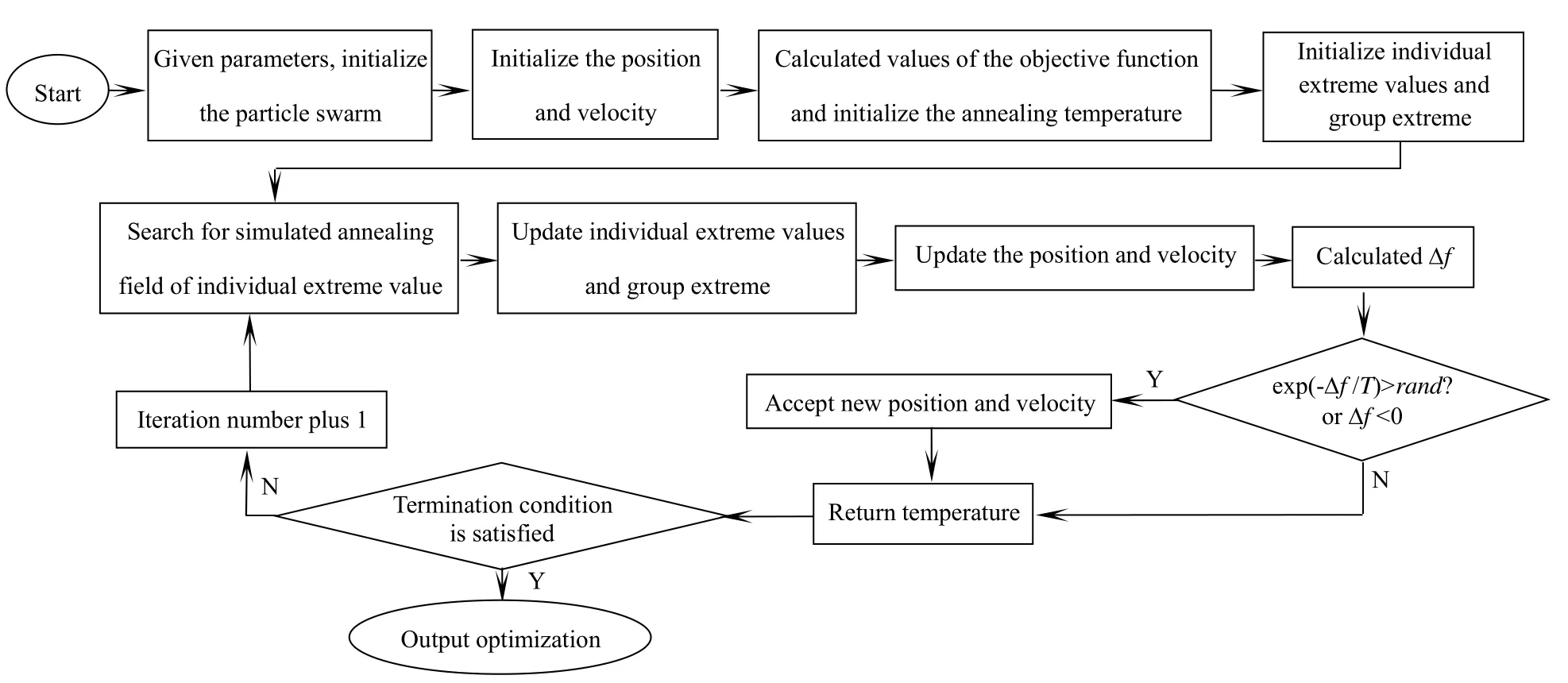
图3 模拟退火粒子群算法wMPS测站布局流程图Fig.3Flow chart of station deployment based on SA-PSO

基于模拟退火粒子群算法的wMPS测站布局流程如图3所示。具体步骤如下：

1)初始化过程如下：

①初始化参数：种群规模m，粒子维度d，学习因子c1，c2，迭代次数。

②初始化粒子位置和速度：由于布站位置具有较高精度的要求，因此本文采用浮点数编码方式进行编码，并随机初始化一定规模的种群，则第i个测站第d维的空间位置和速度可表示为

其中：a，vmax和b，vmin分别代表布站区域和速度的上界和下界;

③初始化退火温度：采用式(8)设定初始化退火温度和退火操作。其中C∈(0,1)。

2)适应度函数：本文采用式(5)作为待优化的适应度函数，将每个粒子的最优适应度值作为初始个体最优适应度值，选择个体最优的极值作为初始群体最优极值；

3)循环操作如下：

①对每个粒子的个体最优值进行模拟退火邻域搜索；

②采用下式更新粒子的速度和位置：

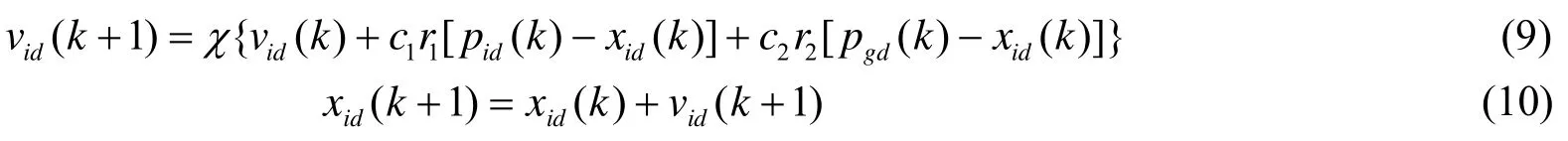
式中：vid(k+1)是粒子在k+1时刻的速度，vid(k)是粒子在k时刻的速度，pid(k)为k时刻个体当前最好位置，pgd(k)为当前全局最优位置。压缩因子其中C=c1+c2。

③更新粒子的个体极值和全局最优值：重新计算每一个粒子的适应值，与该个体初始值进行比较，若优于个体初始值，则更新个体最优值，进而更新全局最优值。

4)模拟退火操作：计算两个位置适应度函数的差值Δf，若Δf＜0或exp(-Δf/T)＞rand则接受新解，利用式(8)进行降温，否则转至第3)步。

5)终止条件：对迭代次数进行判断，如果达到最大迭代次数则输出结果并停止运算。

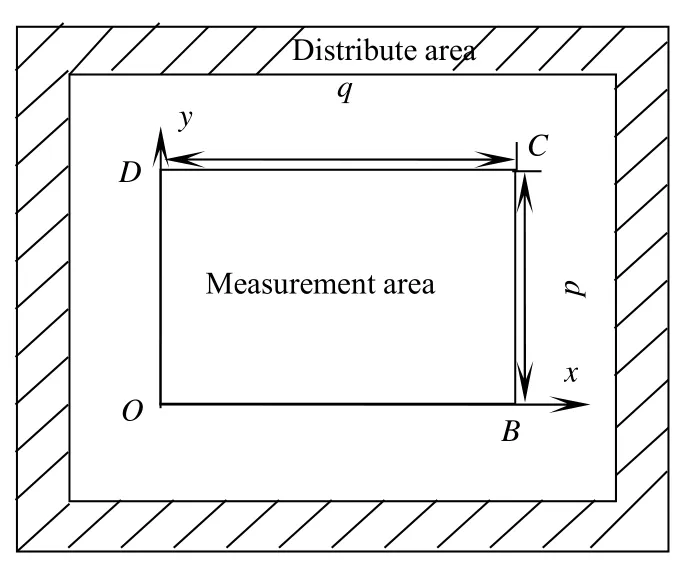
图4 空间约束模型Fig.4Space constraint model

3 仿真结果与分析

3.1 仿真模型建立及算法参数设置

为了简化模型，在不考虑有障碍物的情况下，若被测区域为某高度的平面，如图4所示，设测量区域的外围边界为p×q的矩形，h为被测区域的高度。以被测区域左下角顶点为原点建立局部坐标系Gm,OB连线为x轴正向，OD方向为y轴正向，以O点为坐标系原点，则被测区域M(x,y,z)在Gm坐标系下可表示为[2]

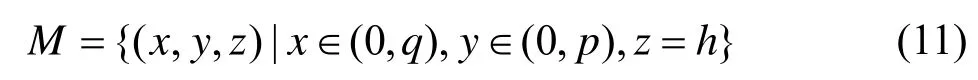
设测量区域q=8 m，p=6 m，h=3 m，同时假设测站均工作在理想状态下，每台测站的作用距离均为4 m～10 m。模拟退火粒子群算法的具体参数设置：种群的规模为50，最大迭代次数Gmax为100，c1，c2等于2，C等于0.5，vmax等于1，vmin等于-1。

3.2 算法仿真

空间约束模型对两到四个测站优化目标运用粒子群算法和模拟退火粒子群算法选取相同权重进行仿真分析，优化前的布局选取经验布局。优化前后测站位置目标函数值变化如表1～表3所示。

表1 两站系统优化前后参数对比Table 1Parameters comparison of two-station system before and after optimization

表2 三站系统优化前后参数对比Table 2Parameters comparison of three-station system before and after optimization

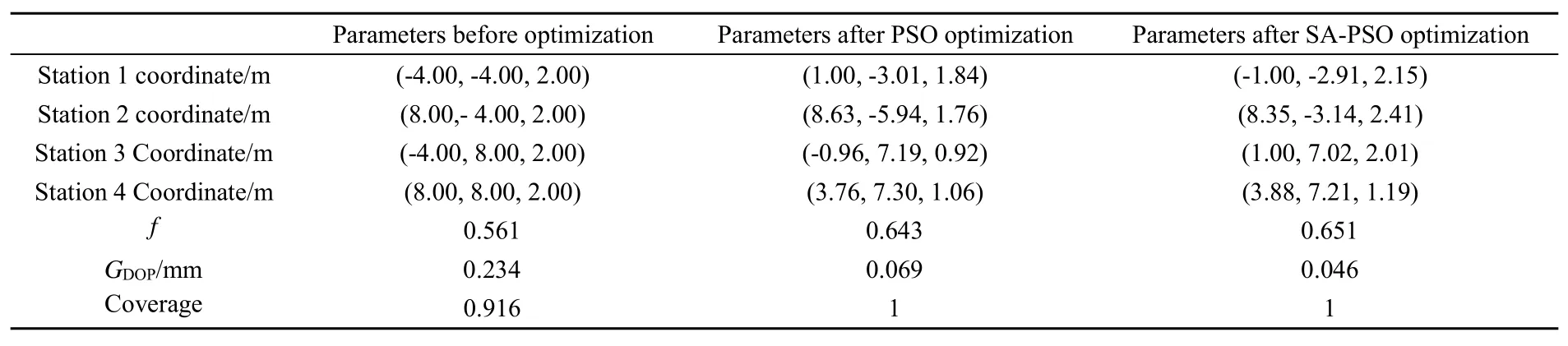
表3 四站系统优化前后参数对比Table 3Parameters comparison of four-station system before and after optimization

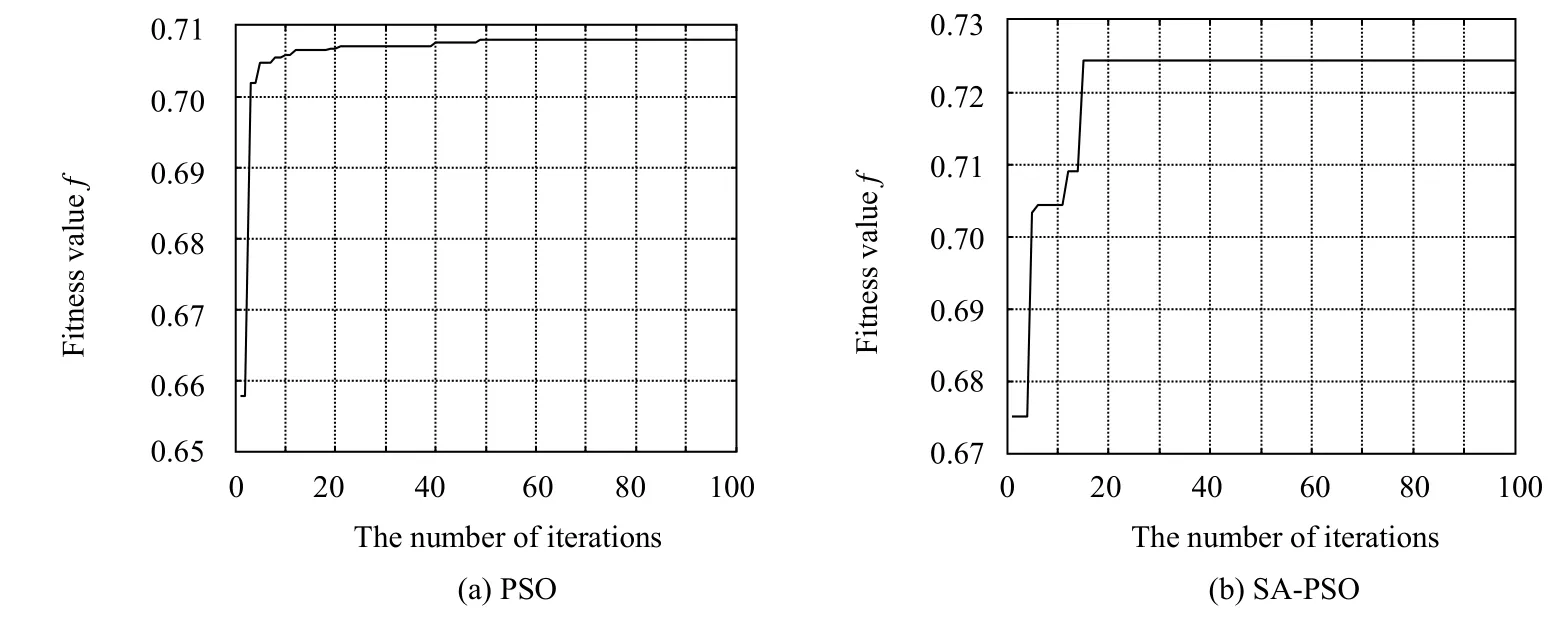
图5 两站系统收敛图Fig.5Convergence curve of network optimization of two stations

③四站系统

选取测站1布站区域为M1={(x∈(-5,1),y∈(-6,-3),z∈(1,3))}，测站2的布站区域为M2={(x∈(3,10),y∈(-6,-3),z∈(1,3))}，测站3的布站区域为M3={(x∈(-5,1),y∈(7,9),z∈(1,3))}，测站4的布站区域为M4={(x∈(3,10),y∈(7,9),z∈(1,3))}。优化后算法最优解收敛图如图7所示。

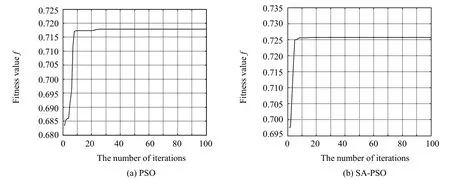
图6 三站系统收敛图Fig.6Convergence curve of network optimization of three stations

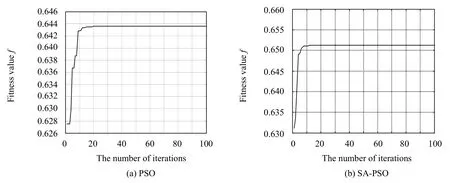
图7 四站系统收敛图Fig.7Convergence curve of network optimization of four stations

3.3 结果分析

从图5到图7两站，三站，四站系统粒子群算法与模拟退火-粒子群算法收敛曲线可以看出，两站系统的f值从0.709增加到0.723，三站系统f值从0.717增加到0.726，四站系统f值从0.643增加到0.651。从前面的目标函数分析可知，f值的增加表明测站在给定的布站区域内获得了较优的布局。在收敛速度方面，使用粒子群算法进行寻优普遍要在30代左右才能获得最优解，而运用本文算法在15代左右就已经获得了最优解，说明本文提出的算法收敛速度较快。而对比表1到表3的两站，三站，四站仿真结果可以看出，相较于优化前及粒子群算法优化后的结果，使用本文提出的模拟退火粒子群算法在目标函数值上都取得了较好的优化结果，每一个目标值都优于或等于其他两个方法获得的最优解。因此，基于模拟退火-粒子群算法的wMPS系统测站部署优化方法是确定空间随机布局的一种有效方法。

4 结论

1)本文从不同测站的交汇情况出发，推导了测站布局与测量系统的定位精度，覆盖度，使用成本之间的关系，从而建立了多目标优化模型。同时提出了一种基于模拟退火算法与粒子群算法相混合的算法，此算法改善了粒子群算法易陷入局部最优的问题，保证了全局收敛性。

2)通过此算法对测站的两站，三站，四站系统的空间随机布局情况进行了仿真研究，并与粒子群算法和经验布局的结果进行对比，发现本文提出的算法能够快速的找到较优的布局，有效地改善系统的测量性能，提高了算法的收敛性。因此，这种方法可以适用于给定布站区域，测量区域对定位精度，覆盖度，使

用成本有要求的空间随机布局的优化过程中。

3)由于本文采用的是等量权重对系统目标函数进行优化设计，并未考虑各个子目标函数对系统测量的重要程度不同，因此下一步将采用层次分析法对权重进行优化设计，以期能更好地发挥各子目标的作用，为工程应用提供参考。

[1]熊芝，邾继贵，耿磊，等.旋转激光平面测角精度测试方法研究[J].激光与红外，2012，42(2)：133-137. XIONG Zhi，ZHU Jigui，GENG Lei，et al.Verification of angle measuring accuracy for rotating planar laser beams[J].Laser &Infrared，2012，42(2)：133-137.

[2]熊芝.wMPS空间测量定位网络布局优化研究[D].天津：天津大学，2012：19-57. XIONG Zhi.Research on network deployment optimization of workspace Measurement and Positioning System[D].Tianjin：Tianjin University，2012：19-57.

[3]Mautz R.Overview of Current Indoor Positioning Systems[J].Geodesy and Cartography(S2300-2581)，2009，35(1)：18-22.

[4]MaurizioG，BarbaraP.Optimalsensorpositioningforlargescalemetrologyapplications[J].Precision Engineering(S0141-6359)，2010，34：563-567.

[5]Schmitt R，Nisch S，Schonberg A.Performance evaluation of iGPS for industrial applications[C]//Proceedings of International Conference on Indoor Positioning and Indoor Navigation(IPIN)，Zurich Switerland，2010：1-8.

[6]熊芝，邾继贵，薛彬，等.空间测量定位网络的典型布局[J].光学精密工程，2013，21(9)：2354-2363. XIONG Zhi，ZHU Jigui，XUE Bin，et al.Typical deployments of workspace measurement and positioning system[J].Optics and Precision Engineering，2013，21(9)：2354-2363.

[7]薛彬，郑迎亚，熊芝，等.室内空间测量定位系统布局仿真研究[J].机械工程学报，2015，51(8)：1-8. XUE Bin，ZHENG Yingya，XIONG Zhi，et al.Simulation for network deployment of indoor workspace Measurement and Positioning System[J].Chinese Journal of Mechanical Engineering，2015，51(8)：1-8.

[8]郑迎亚，邾继贵，薛彬，等.室内空间测量定位系统网络布局优化[J].光电工程，2015，42(5)：20-26. ZHENG Yingya，ZHU Jigui，XUE Bin，et al.Network Deployment Optimization of Indoor Workspace Measurement and Positioning System[J].Opto-Electronic Engineering，2015，42(5)：20-26.

[9]熊芝，邾继贵，耿磊，等.空间测量定位系统测角不确定度分析及检定[J].传感技术学报，2012，25(2)：229-235. XIONG Zhi，ZHU Jigui，GENG Lei，et al.Verification of Angle Measuring Uncertainty for Workspace Measuring and Positioning System[J].Chinese Journal of Sensors and Actuators，2012，25(2)：229-235.

[10]XIONG Zhi，ZHU Jigui，ZHAO Ziyue.Workspace measuring and positioning system based on rotating laser planes[J]. Mechanika(S1392-1207)，2012，18(1)：94-98.

[11]王一，刘常杰，任永杰，等.通用机器人视觉检测系统的全局校准技术[J].光学精密工程，2009，17(12)：3028-3033. WANG Yi，LIU Changjie，REN Yongjie，et al.Global calibration of visual inspection system based on universal robots[J]. Optics and Precision Engineering，2009，17(12)：3028-3033.

[12]莫思敏，曾建潮，徐卫滨.具有自组织种群结构的微粒群算法[J].系统仿真学报，2013，25(3)：445-450. MO Simin，ZENG Jianchao，XU Weibin.Particle Swarm Optimization Based on Self-organization Topology[J].Journal of System Simulation，2013，25(3)：445-450.

[13]孟祥涛，王巍，向政.基于微粒群与模拟退火算法的光纤陀螺导航系统动态补偿方法[J].红外与激光工程，2014，43(5)：1555-1560. MENG Xiangtao，WANG Wei，XIANG Zheng.Dynamic compensation of FOG navigation system based on particle swarm optimization and simulated annealing algorithm[J].Infrared and Laser Engineering，2014，43(5)：1555-1560.

[14]SHAO Wei，ZUO Yijun.Simulated annealing for higher dimensional projection depth[J].Computational Statistics&Data Analysis(S0167-9473)，2012，56(12)：4026-4036.

Station Deployment of Workspace Measuring and Positioning System Based on SimulatedAnnealing Particle SwarmAlgorithm

YUE Chong1a，XIONG Zhi1a,1b，XUE Bin2
(1.a.School of Mechanical Engineering;b.Key Lab of Modern Manufacturing Quality Engineering of Hubei Province, Hubei University of Technology,Wuhan430068,China; 2.School of Marine Science and Technology,Tianjin University,Tianjing300072,China)

Workspace Measuring and Positioning System(wMPS)is a kind of large-scale system,which depends on the multi-station synergy to achieve the coordinate measuring,so the station layout optimization is a common but important problem.Station optimal topological geometry based on simulated annealing particle swarm algorithm was proposed. Firstly,the positioning accuracy,coverage area and cost were taken as objectives to establish the multi-objective optimization function.Secondly,particle swarm algorithm and simulated annealing algorithm were cooperated to find the best solution,and simulated annealing particle swarm algorithm optimization process was established according to multi-objective function.Finally,simulation analysis for layout optimization algorithm of 2～4 stations was performed. The results show that the proposed method has reliable stability and is able to quickly converge to optimal solutions.

large-scale measurement;station deployment;wMPS;simulated annealing particle swarm algorithm

TB92

A

10.3969/j.issn.1003-501X.2016.07.011

1003-501X(2016)07-0067-07

2015-10-30；

2015-12-22

国家自然科学基金(51305130，61505140)；湖北工业大学博士科研启动基金(BSQD12123)资助项目

岳翀(1991-)，女(汉族)，贵州贵阳人。硕士研究生，主要从事大尺寸测量及智能优化算法的研究。E-mail:yoona125@163.com。

熊芝(1985-)，女(汉族)，湖北荆州人。讲师，博士，主要从事大尺寸测量、光电检测方面的研究。E-mail:xiongzhi0611@163.com。