一种用于光电立靶系统的线阵相机现场自标定方法
2016-12-16赵晓理周浦城薛模根
赵晓理,周浦城,薛模根
(1.陆军军官学院,合肥230031;2.偏振光成像探测技术安徽省重点实验室,合肥230031)
一种用于光电立靶系统的线阵相机现场自标定方法
赵晓理1,2,周浦城1,2,薛模根1,2
(1.陆军军官学院,合肥230031;2.偏振光成像探测技术安徽省重点实验室,合肥230031)
针对线阵CCD立靶系统中线阵相机的标定问题,提出了一种现场自标定方法。首先,根据系统测量原理与光学成像原理建立系统线阵相机自标定模型;其次,利用基于局部区域效应的亚像素检测算法检测线阵图像中靶标特征边缘的像素位置;最后,根据自标定函数模型,利用最小二乘法求解像素坐标与实际物理坐标之间的映射关系。整个标定过程既不用求解相机内外参数,也无需将相机与系统分离标定,有效降低了线阵相机标定的复杂度,提高了标定效率。实验结果表明,该方法具有较高精度,满足工程应用需要。
线阵CCD;自标定;立靶;亚像元检测
0 引言
弹丸过靶位置测量是直射武器外弹道参数测试中的一项重要内容,对于衡量武器系统的战术性能具有重要作用。CCD交汇立靶系统具有精确、实时、稳定、安全等优点,因此在弹丸过靶位置测量中得到广泛应用[1-3]。针对高速弹丸过靶位置测量问题,项目组提出了一种利用弹丸穿越激光光幕时形成的阴影与激光
出光口之间的几何关系求解弹丸过靶坐标的线阵CCD光电立靶系统。由于弹丸阴影中心坐标信息由线阵相机拍摄分析得到,因此该系统需要建立线阵相机像素位置与阴影实际位置之间的对应关系,即解决线阵相机的标定问题。
利用传统面阵相机标定方法解决线阵相机标定是目前该领域研究的主要思路,但由于线阵图像无法提取线段、角点等特征,因此标定基元的提取与定位成为了线阵相机标定的主要难题。张洪涛等人[4]通过设计特殊标定靶标,将两步法[5]应用于线阵相机标定中;孙博等人[6]提出一种利用激光跟踪仪辅助标定线阵相机的内外方位参数的方法;刘仁峰等人[7]提出基于二次曲线的线阵相机标定方法;Carlos等人[8]提出了基于非共面特定立体靶标与线阵相机扫描成像的线阵相机标定方法。上述方法虽然都可以精确标定相机参数,但应用于本系统时需将线阵相机从系统中分离出来进行操作,给系统装调与后续应用带来诸多不便,且无法避免相机重新装入系统后由于结构参数微小变化而导致的误差。
目前,线阵CCD交汇立靶系统中对线阵相机标定的通常做法是先根据系统的需要确定标定参数(如有效焦距、光学中心等),再采用不同的标定方法逐一标定[9-10],过程费时费力,工序较为复杂。本文考虑到系统调整完毕后结构参数不会变化,尝试对系统相机进行现场自标定。基本思路是:首先依据系统测量原理与光学成像原理,建立线阵相机自标定模型;再选取多组标定基元的实际物理位置与成像像素坐标带入自标定模型;最后,利用最小二乘法求解自标定模型中转换关系矩阵,得到标定结果。
1 测量系统工作原理
提出的线阵CCD光电立靶系统主要由一字线激光器、激光漫反射板和线阵相机组成,其结构布局如图1所示。其中,L1、L2为两台共面配置且张角均为α的一字线激光器,AB为激光器出光束在漫反射板上形成的光条。两台激光器的光幕ABL1、ABL2共面,线段AL1、BL2相互平行且垂直于AB,长度均为l。阴影区域为两个光幕重合部分,即系统的有效探测区域。线阵相机C在光幕区域外正对AB光条拍摄。
以BL2为X轴,BA为Y轴构造靶面坐标系,则两台激光器的坐标分别为L1(l,y1)和L2(l,0)。当弹丸穿过阴影区域时,AB光条上会出现两处阴影S1和S2,线阵相机实时接收S1、S2的图像信息,并利用标定结果求得阴影中心坐标位置S1(0,y2)、S2(0,y3)。最终,弹丸过靶点G的坐标(x,y)可通过联立直线方程L1S1与L2S2求得:
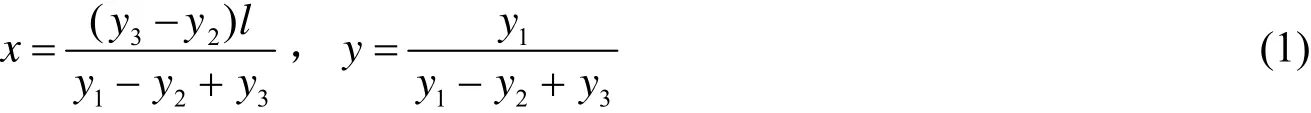

图1 线阵CCD光电立靶原理Fig.1The principle of linear array CCD electro-optical vertical target
2 线阵相机标定模型
2.1 线阵相机针孔成像模型
图2所示为系统中线阵相机的针孔成像模型。其中,D为线阵相机像面,XcYcZc为相机坐标系。将相机坐标系XcYcZc经过旋转与平移形成世界坐标系XwYwZw,使得Xw、Yw分别对应靶面坐标系中的X、Y轴。UV为图像坐标系,由于线阵相机成像为一维线阵图像,因此图像坐标系中V的值为0。当线阵相机C通过成像透镜投影到激光漫反射板上时,满足激光漫反射板与线阵相机视平面交线上任意一点P在图像上的投影位置p,为光心O与P点连线OP与线阵相机像面的交点。

图2 系统线阵相机针孔成像模型Fig.2The pinhole model of system array CCD
由于世界坐标系XwYwZw是由相机坐标系XcYcZc经旋转与平移所得,因此二者的转换关系为
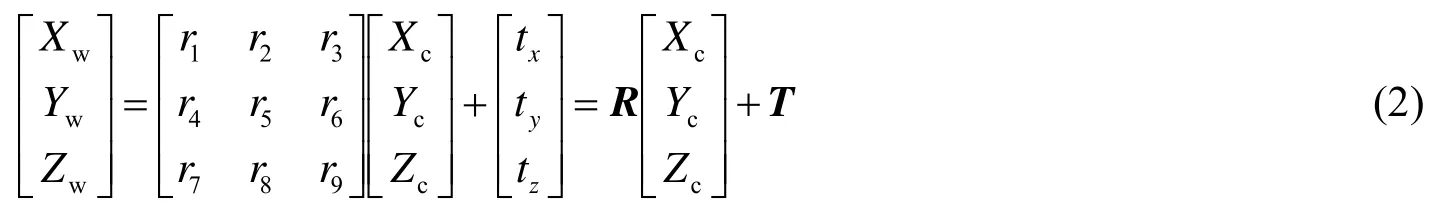
其中:R为旋转矩阵,T为平移矩阵。
鉴于线阵相机C只是为了获取光条上阴影中心的Y坐标信息,因此只考虑世界坐标系中坐标轴Yw与图像坐标轴U的转换关系。根据式(2),P点的yw坐标可用该点的相机坐标表示为

根据针孔成像原理,线阵相机的图像坐标U与摄像机坐标Xc的转换关系为[11-12]

其中:ax是相机u轴的尺度因子(即ax=f/da,da为像元间距),u0是线阵相机的中心像元。
2.2 几何畸变模型
由于实际的镜头会存在不同程度的畸变,因此物点在线阵相机像面上的实际成像与空间点之间存在着复杂的非线性关系。为了确保模型的稳定性,本文只考虑系统线阵相机像素方向上的二阶径向畸变,其可看成在像素方向上对理想成像的拉伸与压缩。根据视觉测量理论,系统线阵相机的二阶镜头畸变值可表示为[13]

其中:u为理想状态下线阵相机的像素点坐标,u'为受到镜头失真影响而造成几何畸变后的实际像素点坐标。为畸变参数。该模型反映了几何畸变后像素坐标与理想像素坐标间的转换关系。
2.3 自标定模型
综合式(3)~式(5),可以得线阵相机像素坐标u'与对应物点实际物理位置yw之间的对应关系为
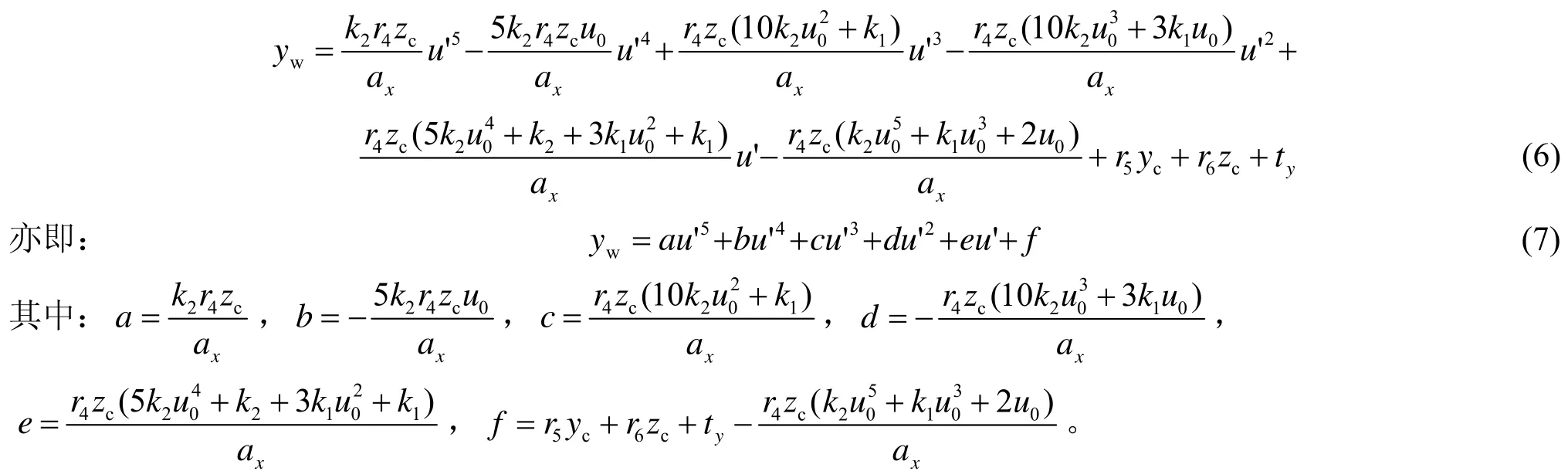
测量系统调整至工作状态后,由于相机正对光条AB拍摄且成像只存在于线阵相机视平面内,因此激光漫反射板与线阵相机视平面交线上任意一点P的yc值均为0,zc为固定值,r4、r5、r6、ty、ax、u0在系统调整固定后皆为常量,从而a、b、c、d、e、f皆为常数,令标定系数矩阵M′=[a b c d e f]T,则式(7)改写:

由式(8)可知,只要求解出M′的值,便得到了像素坐标u'与对应物点实际物理位置yw之间的关系。由于M′中有6个值,因此只需6组标定基元的像素坐标与其实际物理位置便可求出M′。
对于光条AB上n(n≥6)个坐标已知的标定基元都满足式(8),便可得线阵相机的自标定模型:

利用最小二乘法,可求解出标定系数矩阵M′:

3 标定基元亚像元定位
由于线阵图像无法提取线段、角点等特征,因此通常将特定图案的直线边缘作为标定基元。传统边缘检测算子(例如Sobel算子、Canny算子等)可以定位标定基元的像素级边缘位置,为提高线阵相机的标定精度,需要对标定基元边缘进行亚像素精度定位。Agustín等人[14]根据局部区域效应,实现了对二维图像边缘的高精度亚像元定位。受此启发,本文提出一种新的边缘检测模型,使其能够用于一维线阵图像中直线边缘的亚像元检测与定位。
假设边缘的强度值不连续,则直线边缘穿过线阵相机像面上某像素i时,该像素的强度Ii为

如图3(a)所示,假设E为边缘下方的强度,F为边缘上方的强度,SE为边缘下方的面积,SF为边缘上方的面积,h为像素边长,由图可知h2=SE+SF,因此式(11)可改写为

设计窗口为1×3的边缘检测模型如图3(b)所示,当直线斜率在1/3~1/2范围内,根据像素强度不连续假设,边缘直线会分布在线阵相机的三个像素中。以M像素中心位置为原点构建坐标系,x轴与像素方向平行,则边缘在该坐标系中可表示为函数形式为y=ax+b的直线。三个像素的像素强度分别为

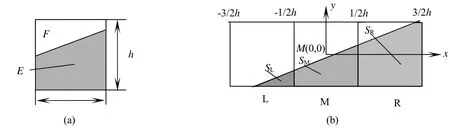
图3 局部区域效应原理(a)边缘像素强度;(b)边缘检测模型Fig.3The principle of local area effect(a)Edge pixel intensity;(b)The edge detection model
三个像素边缘下方面积分别为
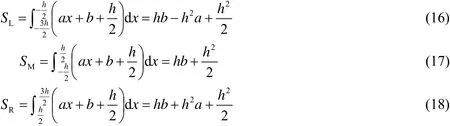
联立式(13)~式(18),可得:


由于线阵相机像素纵轴宽度仅为一个像素,这里只考虑边缘在像素横轴方向上的亚像元位置,选取y=0时x的坐标作为亚像素位置,即:

像素坐标表示为

其中:Mi为模板中心像素的序列号。在进行数值运算时,分别取检测模型两个方向上邻接像素的强度值作为E、F的数值。
利用MATLAB软件构造理想直线边缘一维线阵图像,人工加入高斯噪声,分别采用三次样条插值边缘检测算法[15]、多项式拟合边缘检测算法[16]以及本文算法对仿真图像进行边缘定位,实验结果如表1所示。
分析表1数据可得,三次样条插值算法定位误差均值为0.108 0 pixels,多项式拟合算法定位误差均值为0.071 6 pixels,本文算法的定位误差均值为0.036 7 pixels。由此可得,对于一维线阵图像的直线边缘定位,本文算法具有较高的精度。

表1 边缘定位实验数据Table 1Experiment data of edge position
根据上述算法理论,文章设计宽度为10 mm、精度0.01 mm的黑白条纹图案靶标。为保证边缘区域符合上述边缘检测模型,需要将黑板条纹的直线边缘与线阵相机像素方向成一定角度β,本文设置为23°,图4为黑白条纹图案靶标实物图。

图4 标定靶标Fig.4The calibration target
4 实验与分析
综上所述,系统中线阵相机标定的基本流程为
1)调整系统,将系统调至正常工作状态(即图1所示状态)。
2)将黑白条纹图案靶标安放于系统中激光漫反射板位置,量取靶标上标定基元的实际物理坐标ywi,构成矩阵B。
3)使用系统线阵相机对靶标扫描拍照。
4)对标定图像进行分析,利用式(22)求解标定基元的像素坐标位置u'i,构成矩阵A。
5)利用式(10)求解M′,得到像素坐标与实际物理坐标转换关系,完成标定。
实验选用Basler spL2048-140 km线阵相机,有效像元2 048个,最大输出行频140 kHz,像元尺寸为
10 μm;镜头选用尼克尔镜头,焦距50 mm,最大光圈F=1.4。对照图1,将黑白条纹图案靶标置于光条AB处,启动线阵相机对靶标进行扫描,获取标定图像。根据系统靶面尺寸与标定图像成像情况,选用第650像素到第1 395像素共746个像素为成像有效区域。其中,像素650与1 395皆为标定图像中黑白条纹的边缘像素,定义第650像素为起始像素,序列号为1,则1~746像素区域共有19个黑白条纹,有18处完整的边缘。
为减少噪声干扰,根据线阵相机具有高速扫描频率的特性,在实际应用中首先扫描1 000行靶标图像,再求和取平均值作为标定图像的强度。图5为有效区域去噪后的标定图像强度图。
将有效像素范围的首尾像素所对应在AB光条上的位置设置为标志点,并精确测量标志点位置,设其一维物理坐标分别为由于黑白条纹图案靶标的摆放角度无法保证精度,因此本文根据标定图像中黑白条纹的实际物理宽度相等这一特性,利用式求得黑白条纹实际物理宽度(n为标志点之间的黑白条纹个数),从而确定标志点之间的每个边缘的实际物理坐标ywi。
利用本文算法对标定图像中18处边缘位置进行亚像元定位,获得黑白条纹边缘的像素坐标,结果如表2所示。
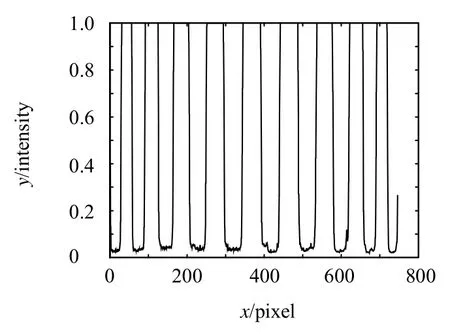
图5 标定图像强度图Fig.5The intensity of calibration image

表2 标定基元坐标Table 2Calibration base element position
最后,将ywi与u'i带入式(10),求得M′。式(23)为实验标定结果,其中yw单位为mm,u'单位为100 pixel。
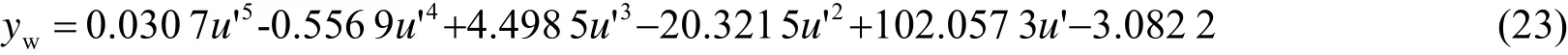
为进一步分析标定结果精度,设计标定精度验证实验。对照图1,在激光漫反射板旁平行于光条AB处设置精密电动平移台,实验选用Zolix公司生产的高精度二维平移台,其重复定位误差小于3 μm。平移台上安装矩形片状黑色挡光元件。将挡光元件调至AB光条处,自下而上平移8次并拍摄,每次平移50 mm(如图6所示)。将图像中遮光元件下沿亚像素位置代入标定结果式(23),求出遮光板下沿物理位置测量
值。最后,平移距离的测量值与平移距离的实际值进行比较,计算误差,完成标定精度的分析。表3为分别使用本文方法、文献[4]标定方法以及文献[7]标定方法进行精度验证实验的结果。

表3 标定验证实验数据Table 3Experiment data of calibration verification experiment
从表3给出的实验数据中可以看出,8组平移中本文方法标定最大绝对误差为0.085 4 mm,最小绝对误差为0.012 1 mm,均值为0.051 8 mm。相同条件下,文献[4]方法标定误差均值为0.097 3 mm,文献[7]方法标定误差均值为0.065 9 mm。由此可得,本文标定方法具有较高的标定精度。

图6 标定验证实验Fig.6Calibration verification experiment
5 总结
本文研究的线阵CCD光电立靶系统线阵相机标定方法具有原理简单、实现方便、标定精度较高等优点。与传统标定方法相比,该方法不需要求出线阵相机的具体参数,从而有效降低了标定工序的复杂性,具有较高的工程应用价值。
[1]董杰,高楼.弹丸任意角度入射弹着点声学检测模型[J].计算机仿真,2015,32(1):10-14. DONG Jie,GAO Lou.Impact Point Detection Model of Bullets Shooting in Any Direction Based on Acoustics[J].Computer Simulation,2015,32(1):10-14.
[2]李翰山,雷志勇,王泽民.两种天幕靶光幕交汇立靶测量系统分析[J].弹道学报,2010,22(1):29-36. LI Hanshan,LEI Zhiyong,WANG Zemin.Analysis of Two Types ofVertical Target Measurement System Measuring Sky-screenAcross Screen[J].Journal of Ballistics,2010,22(1):29-36.
[3]董涛,倪晋平.单线阵CCD相机立靶测量原理[J].应用光学,2011,32(3):482-485. DONG Tao,NI Jinping.Measuring Principle of Vertical Target Based on Single Linear Array CCD Camera[J].Journal of Applied Optics,2011,32(3):482-485.
[4]张洪涛,段发阶,丁克勤,等.基于两步法线阵CCD标定技术研究[J].计量学报,2007,28(4):311-313. ZHANG Hongtao,DUAN Fajie,DING Keqin,et al.Study on Calibration of Linear CCD Based on Two Steps[J].Acta Metrologica Sinica,2007,28(4):311-313.
[5]Tsai R Y.A versatile camera calibration technique for high-accuracy 3D machine vision metrology using off-the-shelf TV cameras and lenses[J].IEEE Journal of Robotics andAutomation(S1070-9932),1987,3(4):323-344.
[6]孙博,邾继贵,任瑜,等.一种利用激光跟踪仪标定线阵相机的方法[J].光电子·激光,2014,25(2):311-316. SUN Bo,ZHU Jigui,REN Yu,et al.A Novel Method for Calibrating Linear Array Camera Based on Lasertracker[J].Journal of Optoelectronics Laser,2014,25(2):311-316.
[7]刘仁峰,龚俊斌,田金文.基于二次曲线的线阵相机标定技术[J].计算机工程,2013,39(1):283-286. LIU Renfeng,GONG Junbin,TIAN Jinwen.Calibration Technology of Line-scan Cameras Based on Quadratic Curves[J]. Computing Engineering,2013,39(1):283-286.
[8]Carlos A L,Manuel M,Jose Luis Lazaro,et al.Calibration of line scan camera[J].IEEE Transactions on Instrumentation and Measurement(S0018-9383),2010,59(8):2185-2190.
[9]朱虹,程松,王栋,等.双线阵CCD相机的畸变校正和标定方法[J].计算机工程与应用,2014,50(22):175-181. ZHU Hong,CHENG Song,WANG Dong,et al.Camera Calibration and Lens Distortion Correction for Binocular Linear CCD [J].Computer Engineering andApplications,2014,50(22):175-181.
[10]雷志勇,姜寿山.线阵CCD技术及其在靶场测试中的应用[J].西安工业学院学报,2002,22(3):221-224. LEI Zhiyong,JIANG Shoushan.Linear Scan CCD Technology and Its Application in Target Measurement[J].Journal of Xi’an
Institute of Technology,22(3):221-224.
[11]杨春晖,韩焱,刘宾.一种线阵CCD显微测量系统的标定方法[J].核电子学与探测技术,2010,30(12):1649-1652. YANG Chunhui,HAN Yan,LIU Bin.Calibration Method for Micro-measurement System Based on Linear CCD[J].Nuclear Electronics&Detection Technology,2010,30(12):1649-1652.
[12]张广军.视觉测量[M].北京:科学出版社,2008:134-173. ZHANG Guangjun.Vision Measurement[M].Beijing:Science Press,2008:134-173.
[13]薛俊鹏,苏显渝.基于两个正交一维物体的单幅图像相机标定[J].光学学报,2012,32(1):145-151. XUE Junpeng,SU Xianyu.Camera Calibration with Single Image Based on Two Orthognal One-Dimensional Objects[J].Acta Optica Sinica,2012,32(1):145-151.
[14]Agustín T P,Karl K,Miguel A F,et al.Accurate subpixel edge location based on partial area effect[J].Image and Vision Computing(S0262-8856),2013,31(1):72-90.
[15]孙秋成,周亚洲,宁闯,等.基于三次样条插值的亚像素边缘检测方法[J].控制工程,2014,21(2):290-293. SUN Qiucheng,ZHOU Yazhou,NING Chuang,et al.A Sub-pixel Edge Detection Method Based on Cubic Spline Interpolation [J].Control Engineering of China,2014,21(2):290-293.
[16]陈静,尚雅层,田军委.快速多项式拟合亚像素边缘检测算法的研究[J].应用光学,2011,32(1):91-95. CHEN Jing,SHANG Yaceng,TIAN Junwei.Fast polynomial fits sub-pixel edge detection algorithms[J].Journal of Applied Optics,2011,32(1):91-95.
AKind of LinearArray Camera Field Self Calibration Method for Electro-optical Vertical Target System
ZHAOXiaoli1,2,ZHOU Pucheng1,2,XUE Mogen1,2
(1.Army Officer Academy,Hefei230031,China; 2.Anhui Province Key Laboratory of Polarization Imaging Detection Technology,Hefei230031,China)
Aiming at the problem of camera calibration of the linear array CCD camera vertical target,a filed self camera calibration method was presented.Firstly,the model of self camera calibration based on the principle of system measurement and the principle of optical imaging was built.And then,a kind of sub-pixel detection algorithm based on partial area effect was used to detect the target characteristic edge’s location in linear image.Finally,the least square was adopted to build the connection between image edge’s pixel coordinate and the corresponding edge’s real coordinate based on the function form of the self camera calibration model.Neither camera’s intrinsic and extrinsic parameters need to be evaluated nor the camera need to be separated from the system through the camera calibration process,so this method has high efficiency with reducing the complexity of calibration.Experimental results show that the proposed cameral calibration method has high precision to meet the demand for project application.
linear array CCD;self-calibration;vertical target;sub-pixel measurement
TP391
A
10.3969/j.issn.1003-501X.2016.07.010
1003-501X(2016)07-0059-08
2015-11-15;
2016-01-14
国家自然科学基金资助项目(61379105);中国博士后基金资助项目(2013M532208)
赵晓理(1991-),男(汉族),安徽合肥人。硕士研究生,主要研究机器视觉。E-mail:670904529@qq.com。
周浦城(1977-),男(汉族),江西宜春人。博士,讲师,从事光电测试与信息处理等方面的研究。Email:zhoupc@hit.edu.cn。
