悬背式箱体结构加强筋布局研究

江川，向春生，刘儒贞

(1.中国科学院光电技术研究所，成都610209；2.中国科学院光束控制重点实验室，成都610209；3.中国科学院大学，北京100049)

悬背式箱体结构加强筋布局研究

江川1,2,3，向春生1,2，刘儒贞1,2

(1.中国科学院光电技术研究所，成都610209；2.中国科学院光束控制重点实验室，成都610209；3.中国科学院大学，北京100049)

为了使悬背式箱体结构具有较好的静动态特性，研究了不同加强筋分布方式对整个箱体结构的影响。结合悬背式光电载荷箱体的实际工况，建立了ANSYS有限元模型；在静态和模态分析基础上，对箱体结构提出了多种改进意见。应用PROE软件对加强筋的形状和位置进行参数化建模，实现不同分布形式的加强筋模型的快速建立。应用ANSYS软件对不同加强筋箱体模型作有限元分析，并将结果分析比较，提出一种折衷评价函数对结果优劣进行评判，选定了最优的加强筋布局方式。最后考虑到整个箱体的实际应用环境，对加强筋的形状尺寸进行了调节，在箱体内部法兰盘处增加了一条纵向加强筋，确定了最终的箱体结构形式。优化后的箱体静态工况最大位移从0.029 mm下降到0.013 mm，达到光电载荷精度要求；一阶谐振频率从88 Hz提高到140 Hz，成功避开80 Hz、85 Hz和100 Hz工作激振频率。悬背式箱体整体性能得到极大提升。该箱体结构已应用于实际光电设备中。关键词：悬背式箱体；参数化；有限元方法；加强筋；评价函数

0 引言

悬背式箱体作为光电载荷的承载结构件，其静态和动态性能的稳定性对整个系统功能的正常实现起着

至关重要的作用[1]。在箱体与其他载荷相互连接的地方，若强度、刚度、谐振频率没有满足要求，就会影响负载设备的正常工作。对于承载有光电设备的箱体，其刚度、谐振频率的要求更为严苛。在结构设计中，一方面要满足箱体在光电载荷、重力、温度耦合作用下的面形精度和位置精度要求，另一方面还要考核箱体结构的动态刚度，即谐振频率和振型，使其避开工况激励点，以免在振动环境中发生共振[2]。除了考虑到箱体的静、动态刚度要求，还要使箱体结构的质量在可以接受的范围。若为了箱体的性能，而单纯的增加壁厚，就会使箱体的质量很大，不满足轻量化设计[2]的要求。通过在结构中适当的位置布置加强筋来提高箱体的性能是一种经济而有效的手段，在工程中应用广泛[3]。而加强筋布局的形式对箱体结构的性能影响很大，若布置位置不合适，就可能使箱体性能不但没有得到改善反而增加了结构质量。因此研究加强筋布局方式具有重要的意义。

目前针对箱体加强筋布局方式的研究主要集中在拓扑优化上[4]。该方法通过对板件的材料分布和厚度进行优化，再参考最优结构的刚度分布来布置加强筋[5]。但由于加筋后结构的刚度等与拓扑优化结构结果有较大的区别，因此拓扑结构优化方法更适用于开发前期确定基体结构，而对于后期比较精确化的设计并不是太实用。本文结合某工程实际，针对悬背式箱体结构进行了研究。该悬背式箱体处于结构设计的后期，结构大体成型，不需要较大的改动。若对其进行拓扑优化，将会加大工作量，提高时间成本。因此本文试图通过比较不同加强筋分布方式对结构性能影响的差异，为以后设计此类悬背式箱体结构提供一种参考。

该箱体作为结构承载件，承载着光电载荷，需要满足一定的静态刚度；并且其工作在振动的环境中，受到80 Hz、85 Hz、100 Hz激励频率，需要使结构的固有频率规避或者高于激励频率点。因此研究悬背式箱体加强筋布局对结构性能的影响是十分必要的。

1 折衷评价函数的建立

刚度、谐振频率、质量是衡量箱体结构优劣的评判依据。刚度大，有利于箱体尺寸精度的稳定；谐振频率高，有利于避免结构共振；质量小，有利于结构轻量化[6]的实现。因此需要综合考虑这三个因素。

式中：k、f、m分别是刚度、一阶谐振频率、质量；w1、w2、w3分别代表权重系数；评价函数的最小值，即为箱体加强筋布局折衷最优解。

2 箱体有限元模型的建立分析

箱体的主要特征是两个法兰盘轴承孔和一个背部立板，如图1。其静态工况如图2，轴承孔孔壁受完全约束A；背部立板上装有负重载荷E，固定在四个螺栓孔上；箱体上承载有两个载荷，一个光电载荷C和一个负重载荷D，占据比较大的空间。箱体材料为铝合金。箱体有限元模型如图3。通过对模型进行静力学分析和模态分析[7-9]，得到位移、模态云图，分别如图4、图5。

由于模型所受应力远远小于材料的屈服极限，故整个分析过程忽略箱体应力分布情况。

从图2可以看到模型的最大位移在背部立板顶端的中间位置，最大位移为0.028 7 mm。由于背部需要支撑光电载荷，对其刚度有比较严格的要求。因此为降低立板的最大位移量，需要加强此处。从图3一阶振型图可以看到，振型集中在悬背立板处，一阶频率为88 Hz，非常接近激振频率85 Hz，容易在正常工作的过程中发生共振现象。针对以上分析结果，对箱体提出了8种不同的加强筋加固方式。

图1 箱体示意图Fig.1Box diagram

图2 箱体受载图Fig.2Box loading figure

图3 箱体有限元模型图Fig.3Finite element model

图4 箱体位移云图Fig.4The displacement nephogram

图5 箱体一阶振型图Fig.5First mode of box

3 加强筋的参数化建模

对模型进行参数化建模[10]，可以高效率的对模型进行更改。箱体结构主体已基本定型，只需对加强筋的形状尺寸和位置尺寸进行参数化建模，实现加强筋不同尺寸和形状的快速更改成型。利用PROE软件的参数化建模功能，实现了不同加强筋模型的建立。加强筋加固形式为

0)最初模型：28.303 kg；1)悬背后侧加矩形筋:28.457 kg；2)悬背前侧加两三角形筋：28.484 kg；

3)悬背前侧中间位置加矩形筋：28.514 kg；4)悬背前侧加两矩形筋：28.665 kg；

5)悬背前侧加三矩形筋：28.876 kg；6)悬背后侧加厚：29.403 kg；

7)悬背加厚及两侧加矩形筋：29.765 kg；8)悬背加厚及前侧加三矩形筋：29.976 kg

由于加固形式增多，呈现具有代表性的造型如图6。

图6 加固方式Fig.6Methods of reinforcement

4 结果分析

不同加强筋模型的有限元建模方式参照最初模型，并保证加强筋成为唯一的分析变量，这样对比结果才具有说服力。通过对不同模型的分析比较，得出表1。序号对应表1加固方式。

通过表1，可以看到。在背部加厚和悬背前侧加两矩形筋对立板，刚度的提升是最大的，最大位移均为0.015 mm左右，并且整个结构的一阶频率也得到了提高，从开始的88 Hz变化到110 Hz以上；三角形筋的效果弱于矩形筋，以及立板后侧加矩形筋的效果也不是太好。序号7、8是对前述6种中比较合理加强筋布局的组合，效果非常明显，最大位移小于0.012 mm，一阶频率提高到150 Hz左右。

根据折衷评价函数式(1)，对不同加强筋布局的箱体结构性能进行定量分析。该箱体的优化注重动态谐振频率的优化，且质量、刚度需要在可接受的范围。因此对w1、w2、w3分别取值0.2、0.7、0.1。基于评价函数下的评价数值结果如图7。

通过图7可以看到，序号8所对应的加强筋箱体模型具有最小的折衷评价数值，因此选择8号加强筋布局形式。

表1 不同加强筋箱体分析结果对比Table 1Results contrast of different stiffeners

图7 评价函数结果Fig.7Evaluate value curve

5 最终模型的建立

箱体通过分析比较，确定了以背部立板加厚及前侧加三矩形筋的方式进行加固。箱体在实际情况下，立板上安装有箱盖。考虑到与箱盖的配合关系，将矩形筋的尺寸进行了修改。立板刚度的提高，也导致了箱体三阶振型的变化，振动方式是沿着法兰盘轴向运动，箱体上方有较大的突起。基于轴向稳定性的考虑，将箱体内部筋进行了调节，调节位置如图8，最终优化模型如图9。经过调整后的箱体，其三阶振型的变化如图10，三阶频率从203 Hz变化到220 Hz，法兰盘轴向的动态刚度得到提升。最后将最终模型和最初模型进行分析比较，如表2。

图8 内部筋调整前后Fig.8Contrast of internal stiffeners

图9 最终优化模型Fig.9The optimization model

图10 内部筋调节后三阶振型Fig.10Contrast of third order vibration

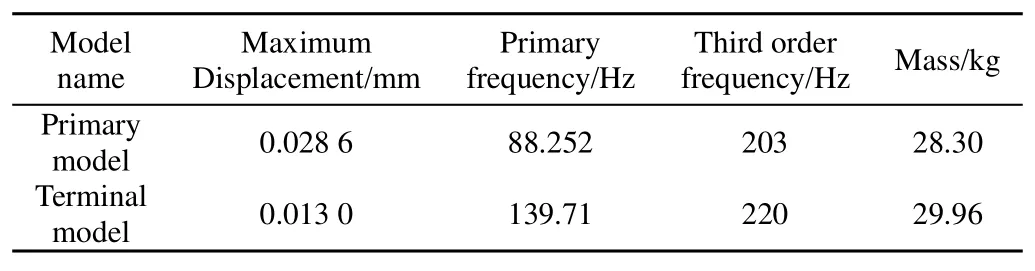
表2 最初和最终模型比较Table 2Results contrast of original and optimized model

由表2可以看出，经过加强筋加强后的优化模型，最大位移降低到0.013 mm，是最初模型的一半，立板处的刚度得到了加强；谐振频率特性也由最初的88 Hz上升到140 Hz，提高了箱体规避低阶振动的能力。

6 结论

悬背式箱体作为光电载荷的承载结构件，其静态和动态性能的稳定性对整个系统功能的正常实现起着至关重要的作用。文章通过对几种不同加强筋分布方式的分析比较，明确箱体在静动态环境下，结构变形的表现形式，并结合自定义的评价函数，选定了最优的箱体结构加固形式。整个优化过程简单有效，减小了研发的时间成本，并为以后悬背式箱体结构的优化提供了参考。该箱体在质量仅增加1.6 kg的情况下，静态最大位移从0.029 mm下降到0.013 mm，一阶频率由最初的88 Hz提高到140 Hz。箱体整体性能得到极大的提高。本文所得的箱体已应用于实际光电设备中。

[1]梁醒培，王豪，张锴锋.大型齿轮箱结构分析与结构优化[J].机械设计与制造，2008，1(1)：31-33. LIANG Xingpei，WANG Hao，ZHANG Kaifeng.The structure analysis and optimization of gearbox with large size[J]. Machinery Design&Manufacture，2008，1(1)：31-33.

[2]李志来，徐宏.长条形空间反射镜及其支撑结构设计[J].光学精密工程，2011，19(5)：1040-1046. LI Zhilai，XU Hong.Design of rectangular space mirror and its support structure[J].Optics and Precision Engineering，2011，19(5)：1040-1046.

[3]赵雨旸，周欢，李涵武.基于有限元分析的减速器箱体优化设计[J].林业机械与木工设备，2009，8(8)：28-30. ZHAO Yuyang，ZHOU Huan，LI Hanwu.Optimal design of a Reducer Casing Based on Finite Element Analysis[J].Forestry Machinery&Woodworking Equipment，2009，8(8)：28-30.

[4]刘书田，胡瑞，周平，等.基于筋板式基结构的大口径空间反射镜构型设计的拓扑优化方法[J].光学精密工程，2013，21(7)：1804-1810. LIU Shutian，HU Rui，ZHOU Ping，et al.Topologic optimization for configuration design of web-skin-type ground structure based large-aperture space mirror[J].Optics and Precision Engineering，2013，21(7)：1804-1810.

[5]刘海，高行山，王佩艳，等.基于拓扑优化的结构加强筋布局降噪方法研究[J].振动与冲击，2013，32(13)：1803-1810. LIU Hai，GAO Hangshan，WANG Peiyan，et al.Stiffeners layout design for noise reduction using topology optimization[J]. Journal of Vibration and Shock，2013，32(13)：1803-1810.

[6]范磊，张景旭，吴小霞，等.大口径轻量化主镜边缘侧向支撑的优化设计[J].光学精密工程，2012，20(10)：2207-2212. FAN Lei，ZHANG Jingxu，WU Xiaoxia，et al.Optimum design of edge-lateral support for large-aperture lightweight primary mirror[J].Optics and Precision Engineering，2012，20(10)：2207-2212.

[7]孙野，殷凤龙，杨丹，等.复杂激励下变速箱箱体动态响应分析[J].机床与液压，2014，42(19)：78-81，96. SUN Ye，YIN Fenglong，YANG Dan，et al.Dynamic Analysis of Gearbox Housing under Complex Dynamic Excitation[J]. Machine Tool&Hydraulics，2014，42(19)：78-81，96.

[8]高立强，奚鹰，圣亚运，等.带肋轮边减速器箱体的有限元分析与优化[J].中国工程机械学报，2015，13(1)：29-33. GAO Liqiang，XI Ying，SHENG Yayun，et al.Finite element analysis and optimization on ribbed wheel-rim reducer case under combined working conditions[J].Chinese Journal of Construction Machinery，2015，13(1)：29-33.

[9]苗继军.EBH160横轴掘进机电机箱体有限元分析[J].煤矿机械，2015，36(4)：130-132. MIAO Jijun.Finite Element Analysis of Motor box for EBH160 Horizontal Roadheader[J].Coal Mine Machinery，2015，36(4)：130-132.

[10]张昌明.圆柱齿轮减速器下箱体参数设计与快速原型制作研究[J].陕西理工学院学报，2008，24(2)：5-8. ZHANG Changming.Cylindrical gear reducer lower-case parameterized design and rapid prototyping manufacturing[J]. Journal of Shanxi University of Technology，2008，24(2)：5-8.

Stiffeners Layout Design for Hanging-back Box

JIANG Chuan1,2,3，XIANG Chunsheng1,2，LIU Ruzhen1,2
(1.Institute of Optics and Electronics,Chinese Academy of Sciences,Chengdu610209,China; 2.Key Laboratory of Optical Engineering,Chinese Academy of Sciences,Chengdu610209,China; 3.University of Chinese Academy of Sciences,Beijing100049,China)

In order to improve the static and dynamic characteristics of hanging-back box,the effect of different stiffeners distribution modes was researched.Combined with engineering practice of a hanging box with photoelectric load, ANSYS model was set up and eight kinds of suggestions were presented based on the static and modal analysis results. PROE was applied to set up the parametric model,which can achieve models with different distribution forms of stiffeners in a shorter time.ANSYS was applied to analyze the box with different stiffeners,and a compromise evaluation function was presented to help select the best way of strengthening.At last,considering the practical application of the box,the size of stiffeners was changed and a longitudinal stiffener was added.In conclusion,the static maximum displacement of the optimized box reduced from 0.029 mm to 0.013 mm,meeting the accuracy requirement and the fundamental frequency increased from 88 Hz to140 Hz avoiding the vibration frequency points including 80 Hz,85 Hz and 100 Hz.The box has been used in a photoelectric device.

hanging-back box;parametric;finite element method;stiffeners;evaluation function

TH122;TB21

A

10.3969/j.issn.1003-501X.2016.07.007

1003-501X(2016)07-0040-05

2015-08-17；

2015-10-23

江川(1990-)，男(汉族)，重庆璧山人。硕士研究生，主要研究工作是光机结构设计。E-mail:751906994@qq.com。