加筋板整体屈曲临界应力计算与分析
2011-03-06王伟吴梵
王 伟 吴 梵
海军工程大学 船舶与动力学院,湖北 武汉 430033
加筋板整体屈曲临界应力计算与分析
王 伟 吴 梵
海军工程大学 船舶与动力学院,湖北 武汉 430033
利用解析法对加筋板稳定性进行了研究,忽略材料非线性的影响,利用理论方法求解四边简支加筋板的整体屈曲临界应力。对有一根加强筋的加筋板,定义板的挠曲函数,将其代入边界方程和协调方程,求解线性方程组的特征方程得到加筋板的临界应力。对有2根或多根加强筋的规则加筋板,利用能量法导出统一计算的公式得到临界应力。最后,利用有限元软件Abaqus和Nastran进行数值仿真,与理论解比较后得出本文计算方法是正确的,可以准确求解加筋板的稳定性问题。
加筋板;稳定性;整体屈曲;临界应力
1 引言
屈曲问题是船舶设计中的重要问题,历来受到船舶力学工作者的高度重视[1]。现代船舶随着功能的多样化,结构形式更加复杂,为了保证船体结构的安全,必须对其稳定性进行研究。加筋板是船体的主要组成结构,对其稳定性的研究是船舶稳定性研究的基础。许多学者都进行了加筋板的稳定性研究[2-7],其中绝大多数是采用有限元法进行研究,缺乏理论指导,没有给出统一的计算公式,本文利用解析法,研究了加筋板的屈曲问题,给出了规则加筋板临界应力的统一计算公式,使加筋板的临界应力计算简单可靠,可以用来指导工程实践。屈曲从失效模式上分为局部屈曲和整体屈曲,整体屈曲对船舶结构的影响更大,所以本文只研究加筋板的整体屈曲问题。在计算过程中,为了简化理论推导,忽略了材料非线性的影响,本文只研究加筋板的弹性屈曲问题。
2 理论分析
2.1 基本模型
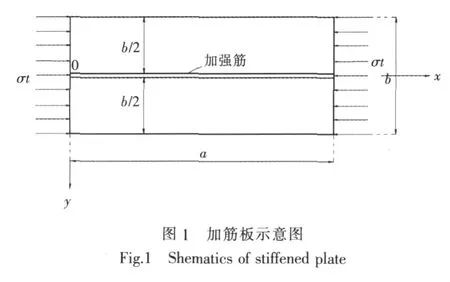
一块长度为a,宽度为b,厚度为t的矩形板,四边简支连接,该板在中线上有一纵向加强筋,加强筋的截面积为A,惯性矩为I。假定加强筋的抗扭刚度相当小,可以忽略不计,只考虑加强筋在垂直于板面方向的抗弯刚度,如图1所示,加筋板单向受压,板在x=0和x=a的2条边上承受均布荷载σt,加强筋具有和板相同的压应力。
2.2 屈曲模式分析
首先引入下列符号:
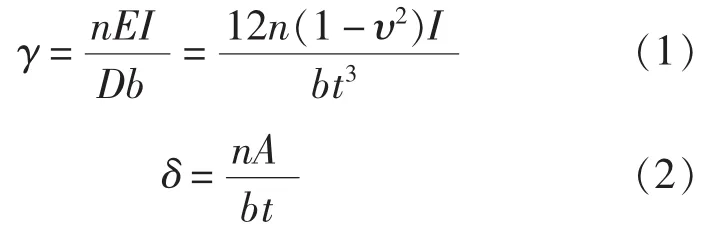
式中,系数γ为加强筋的抗弯刚度与宽度为b的板的抗弯刚度的比值;δ为加强筋的横截面积与板的横截面积bt的比值;n为加强筋的数量。
由于板和加强筋组成的加筋板是对称于x轴的,在屈曲后所发生的位移形式有以下2种情况:对称形式—加强筋和板一起发生挠曲,即加筋板的整体屈曲;反对称形式—加强筋保持为直线,加强筋两侧的板各自发生挠曲,即加筋板的局部屈曲。在后一种情况中,板在屈曲后有一波节线,它和加强筋的轴相重合,板的每一半就相当于长度为a,宽度为b/2的四边简支板,此时,板和加强筋组成的加筋板的屈曲荷载达到其最大值。
加筋板的刚度比值γ较小时,加筋板出现对称位移形式,此后随着γ的逐渐增大,加筋板的临界应力逐渐增大,当γ大于某一数值γ0时,加筋板出现反对称的位移形式,此后加筋板相当于2块四边简支的板和加强筋各自发生挠曲,加筋板的临界应力与筋无关,而是等于宽度为b/2的简支板的临界应力。临界值γ0是与加筋板产生反对称屈曲形式所必需的加强筋的最小抗弯刚度相对应的,求出γ0就可以直接判断加筋板是发生对称屈曲还是发生反对称屈曲。当γ>γ0时,加筋板发生反对称屈曲,加筋板的临界应力达到最大值,这在工程实际中很少遇到,即使遇到也可以容易求解,所以本文主要研究在γ<γ0时的对称屈曲情况。
2.3 临界应力求解
假设屈曲板的挠度表达式为[8]:
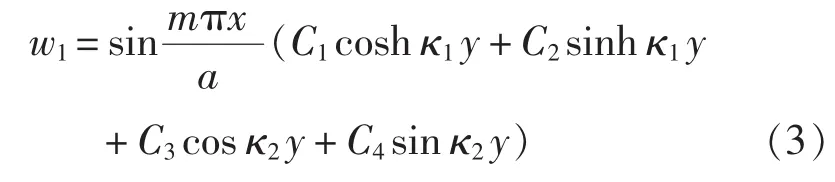
式中,w1为板的下半部分的挠度。由于对称关系,板的另一半的挠度w2可立即得到。κ1和κ2的表达式为:

式中,Q1和Q2为靠近加强筋的板在单位长度内的剪切力。

加强筋的轴向荷载为σcA,将加强筋简化为单跨梁,它的挠度w的微分方程式为:


将式(3)分别代入式(6)、式(7)、式(15),求解线性方程组的特征方程得到对称屈曲形式的稳定条件:
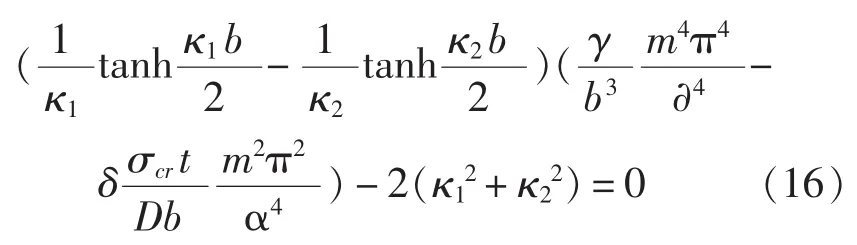
将式(4)、式(5)代入式(16),对不同的半波数 m求出相应的μ,回代式(5)得到该屈曲模式下的临界应力为:

2.4 两根相同加强筋规则布置的情况
如图2所示单向受压的四边简支板上有2根加强筋,加强筋将板等分为3份,由于加强筋尺寸相同,而且均匀布置,因此加筋板将发生关于板面中线的对称屈曲或3个半波的反对称屈曲,不会发生其他形式的屈曲。发生反对称屈曲时的临界应力可以利用板的屈曲理论求得,在此不作讨论,主要研究发生对称屈曲时情况。

若用上面类似方法进行求解,协调方程难以确定,下面采用能量法计算多根加强筋的加筋板整体屈曲临界应力。加强筋均匀布置,加筋板为对称结构,根据板架的简化计算模型[9],假设四边简支加筋板的挠度为:
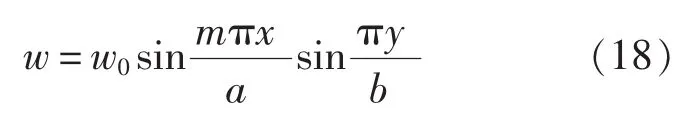
式中,m为x方向的半波数;y方向为对称屈曲形式,只有1个半波。
板的应变能为:
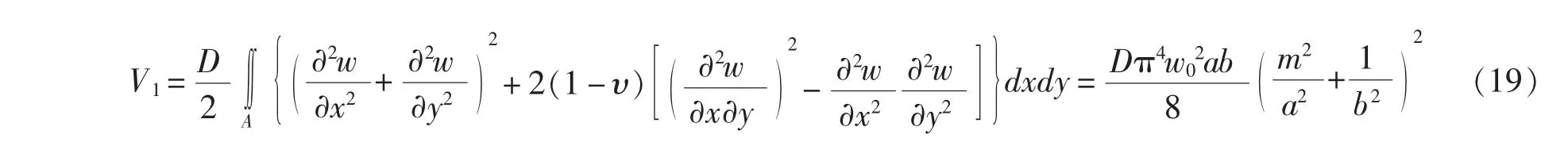

式中,Nx为板上作用的均布压力,且 Nx=σcrt;t为加筋板的板厚。
加强筋的外力功为:
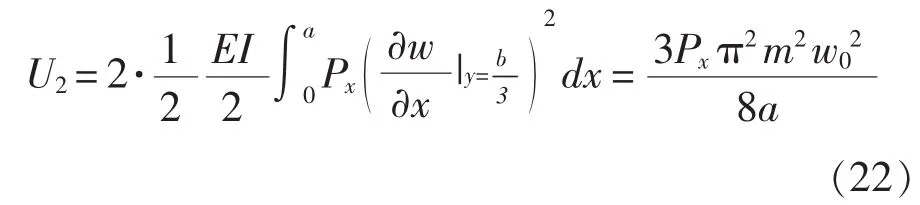
式中,Px为加强筋上作用的轴向力,且Px=σcrAx;Ax为加强筋的截面积。
根据Timoshenko提出的能量法,如果加强筋的外力功小于其应变能,加强筋是稳定的;如果外力功大于应变能,加筋板是不稳定的[10]。利用外力功等于应变能可以确定加筋板对称屈曲时的临界应力,简化得到:
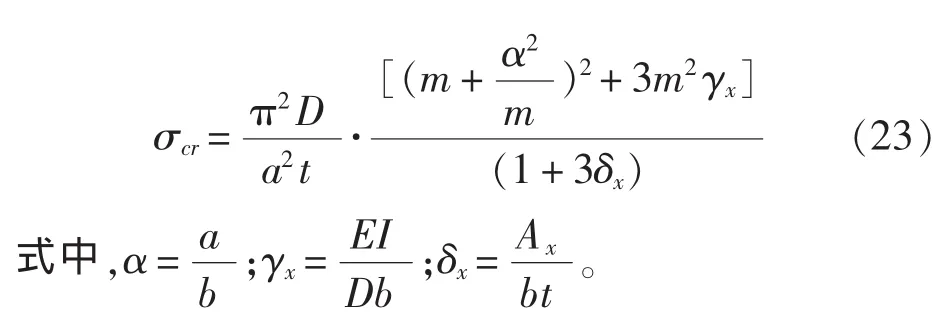
求出最小的σcr便得到加筋板的临界应力,此时对应的m值为x方向的半波值。
2.5 多根相同加强筋规则布置的情况
3根相同加强筋均匀布置的加筋板示意图如图3所示。
挠曲线仍取上面的函数为:
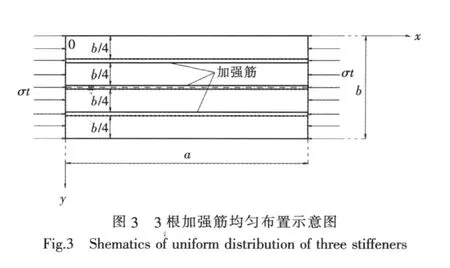

根据相关参考文献中提到的加筋板临界应力统一公式的推演过程,结合上面的推导,得到如下结论:对于相同加强筋均匀布置的规则板架,其发生整体失稳时,在y向屈曲成一个半波,且临界应力为:
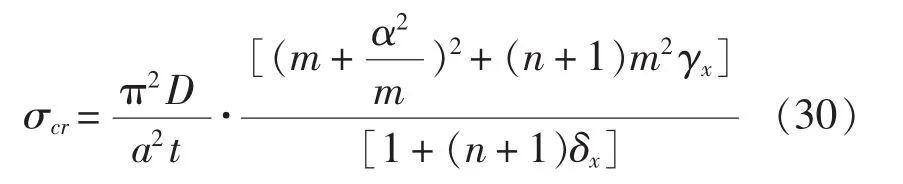
式中,n为加强筋的数目。
此公式具有一定的通用性,可以方便计算规则加筋板的临界应力。
3 算例分析
3.1 一根加强筋置于简支板中的情形
板和加强筋示意图如图4所示。
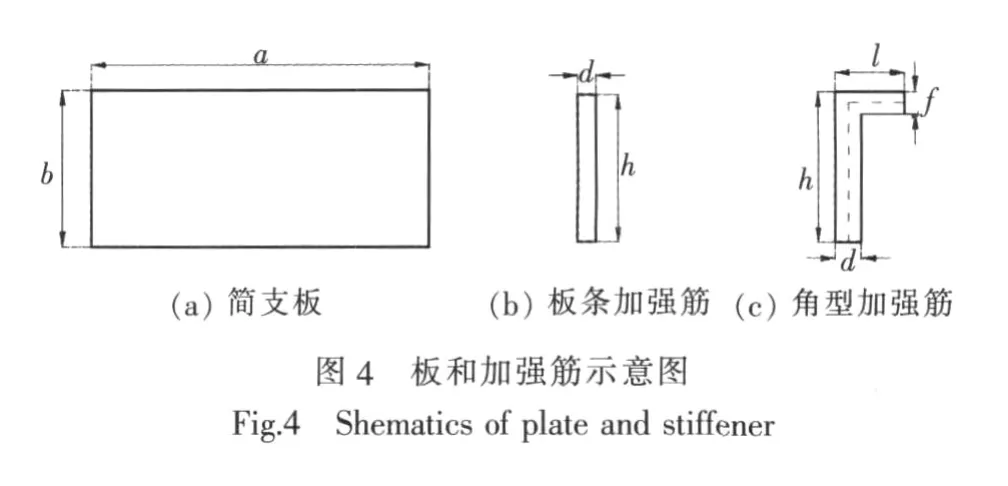
板四边简支,加强筋纵向布置在板中间,加筋板纵向受压,板和加强筋采用相同的材料,E=205 800 MPa,υ=0.3。 利用本文方法求得理论解,同时利用有限元软件Abaqus和MSC.Nastran进行数值仿真,将有限元解与理论解进行比较。
3.1.1 板和加强筋的尺寸都发生变化的情况
取12个算例,板和加强筋的尺寸都在发生变化,研究各参数对临界应力的影响,计算结果如表1所示,临界应力随γ的变化曲线如图5所示。
从表中数据和图中曲线可以得出如下结论:
1)Abaqus计算的结果与理论值较接近,用其进行数值仿真,所得结果更加准确;
2)板的尺寸较加强筋的尺寸对临界应力影响大一些,在板和加强筋的尺寸都发生变化时,首先关注板尺寸的变化;
3)加强筋的高度比厚度对临界应力影响大一些;
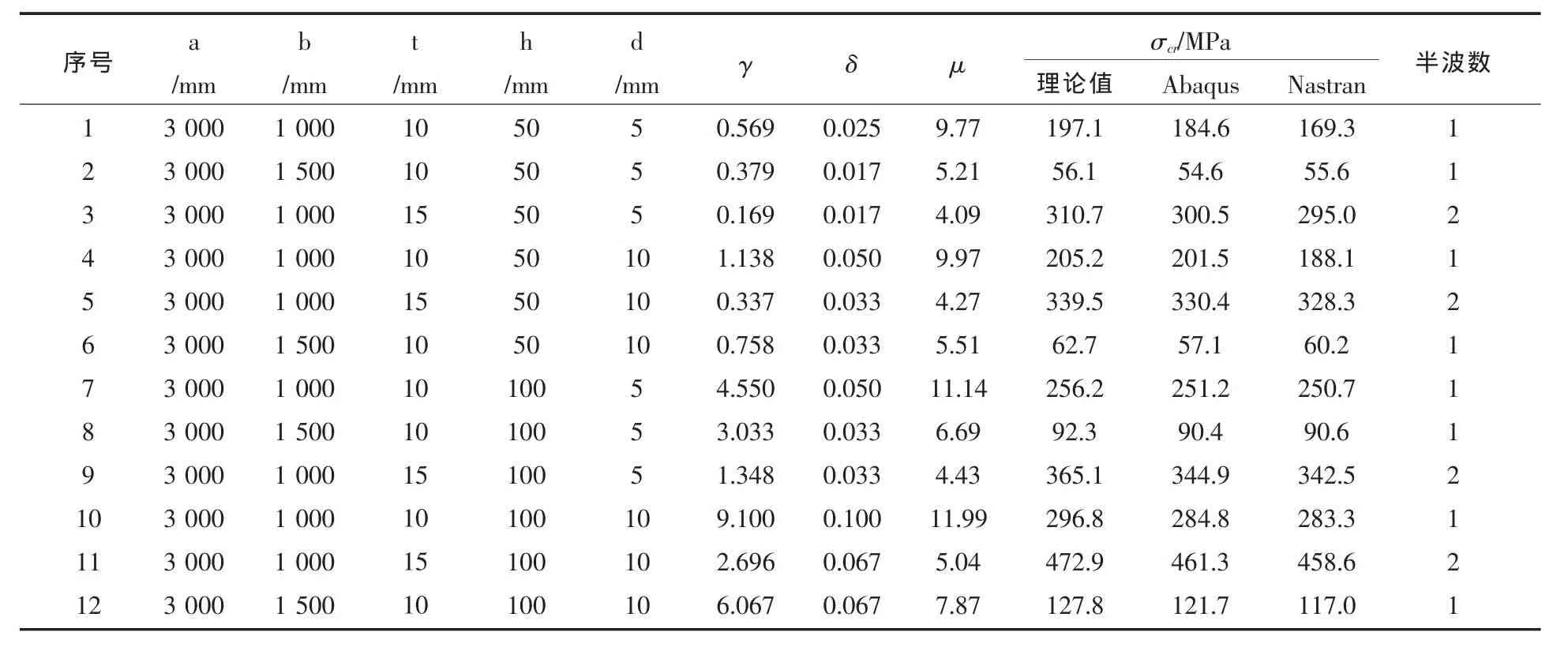
表1 板和加强筋尺寸均发生变化的临界应力计算表Tab.1 Camputation sheet of critical stress varying with the sizes of plate and stiffener
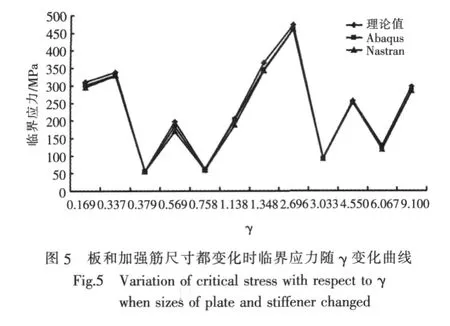
4)在各参数都变化时,临界应力与γ没有完全的线性增长关系,不能仅根据γ的变化判断临界应力的变化,还要参考其他数据;
5)理论计算结果较有限元解偏大。这主要是由于挠度表达式中所选的项数太少,这样计算相对简单,但使结果偏大,增加挠度表达式的项数就可以使结果更加准确。
3.1.2 板宽发生变化,其他尺寸均不变
板尺寸对临界应力的影响很大,取4个算例,板的宽度发生变化,其它尺寸不变,研究板宽单独变化对临界应力的影响,计算结果如表2所示,临界应力随γ和δ的变化曲线如图6和图7所示。

表2 板宽发生变化的临界应力计算表Tab.2 Computation sheet of critical stress varying with width of plate
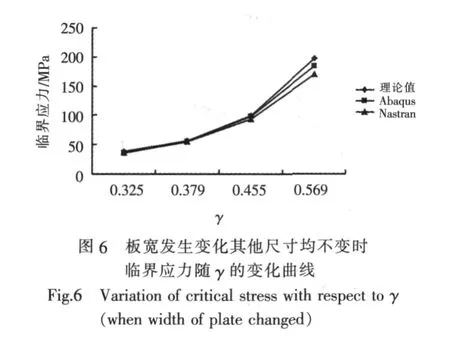
从表中数据和图中曲线可见:
1)随着板宽的增加,临界应力减小的幅度越来越小;
2)临界应力随γ和δ的增大而增大,增长幅度越来越大。
3.1.3 板厚发生变化,其他尺寸均不变

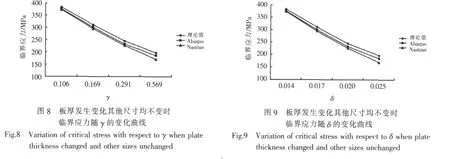
取4个算例,板的厚度发生变化,其他尺寸不变,研究板厚单独变化对临界应力的影响,计算结果如表3所示,临界应力随γ和δ的变化曲线如图8、图9所示。
从表中数据和图中曲线可见:临界应力随γ和δ的增大而减小,减小幅度越来越小;随着板厚的增加,加筋板的屈曲半波数发生变化。

表3 板厚发生变化的临界应力计算表Tab.3 Computation sheet of critical stress varying with the plate thickness
3.2 多根加强筋均匀布置的情况
利用有限元软件Abaqus和Nastran进行仿真计算,得出多根加强筋时加筋板稳定性的规律。材料属性同上,加强筋采用板条加强筋和L型加强筋。
3.2.1 多根板条加强筋的情况
取 4个算例,板条加强筋的根数为 2、3、4、5,研究加筋板临界应力随根数的变化规律,计算结果如表4所示,临界应力随γ和δ的变化曲线如图10和11所示。

表4 多根板条加强筋临界应力计算表Tab.4 Computation sheet of critical stress of stiffener with multiple slabs

从表中数据和图中曲线可见:
1)临界应力随γ和δ的增大而增大;
2)随着板条加强筋数量的增加,加筋板屈曲的半波数并没有发生变化,说明加强筋的数量并不是影响屈曲模式的主要因素。
3.2.2 多根L型加强筋的情况
取 4 个算例,L 型加强筋的根数为 2、3、4、5,研究加筋板临界应力随根数的变化规律,计算结果如表5所示,临界应力随γ和δ的变化曲线如图12和13所示。

表5 多根L型加强筋临界应力计算表Tab.5 Computation sheet of critical stress of stiffener with multiple L slabs
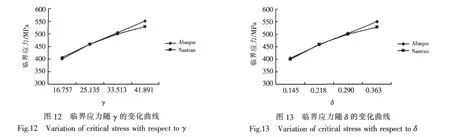
从表中数据和图中曲线可见:
1)临界应力随γ和δ的增大而增大;
2)L型加强筋比板条加强筋对加筋板的临界应力影响大。
4 结论
通过理论分析和算例比较,可以得到如下结论:
1)本文导出的解析方法简单可靠,可以求解加筋板的弹性屈曲问题,具有重要的理论价值,为更加复杂结构的弹性屈曲问题求解奠定理论基础。
2)加强筋的尺寸和形状影响加筋板的临界应力,但板的尺寸,特别是厚度对临界应力的影响比加强筋的尺寸影响更大。
3)加筋板的屈曲模式受板的厚度,加强筋的尺寸和位置的影响,由多种条件共同制约。
4)有限元软件Abaqus和Nastran对同一问题所得的结果有偏差,这是由于它们采用的求解器不同。Abaqus软件采用Subspace法进行求解,而Nastran软件采用Lanczos法进行求解。
5)本文忽略了材料的非线性影响,只求解加筋板的弹性屈曲临界应力,没有对结果进行非线性修正,这和实际情况有所差别,需要在后面的研究中解决非线性的影响。
[1]俞铭华.船舶板架稳定性研究进展[J].华东船舶工业学院学报,2000(4):20-25.
[2]徐向东,崔维成.加筋板格屈曲及极限强度分析[J].中国造船,1999(1):68-76.
[3]郭彦林,梅占馨.加筋板的非线性相关屈曲研究[J].应用力学学报,1992(2):47-57.
[4]邱瑞强.用有限元法求解轴压加筋板的几何非线性稳定性问题[J].上海力学,1985(2):66-75.
[5]朱菊芬,周承芳.加筋板壳稳定性分析中一种简单的有限元模式[J].应用力学学报,1993(4):113-118.
[6]胡毓仁,陈伯真,孙久龙.纵向受压加筋板架有侧向压力时加强筋的扭转屈曲 [J].上海交通大学学报,2000(12):1717-1722.
[7]戴承伟,王永亮.加筋板稳定性微分求积单元法分析[J].南京航空航天大学学报,2007(5):642-645.
[8]F.柏拉希.金属结构的屈曲强度[M].北京:科学出版社,1965:362-375.
[9]于杰.面内载荷作用下船体结构的稳定性分析 [D].武汉:武汉理工大学,2005.
[10]张常伟.加筋板稳定性承载能力的研究 [D].上海:上海海事大学,2006.
Computational Analysis on the Critical Stress of Stiffened Plates′Overall Buckling
Wang WeiWu Fan
College of Naval Architecture and Power,Naval University of Engineering, Wuhan 430033, China
The paper used analytical method to deal with the stability problem of stiffened plates, by ignoring the influence of material's nonlinearity, it employed theoretical method to resolve critical buckling stress of stiffened rectangular plate with simplified supporting.For single stiffened plate, the deflection function was defined and introduced to boundary equation and coordinate equation,which acquired the critical stress of stiffened plate by solving linear equations.For plate with two or more stiffeners, the paper acquired the critical stress through uniform formulation using Energy Method.The results of numerical simulation by using Abaqus and Nastran were compared with theoretical solutions,the validity of analytical method was verified, it can be used to solve the stability problem of stiffened plates.
stiffened plate; stability; overall buckling; critical stress
U661.31
A
1673-3185(2011)03-21-07
10.3969/j.issn.1673-3185.2011.03.005
2010-05-27
王 伟(1985-),男,硕士研究生。研究方向:船舶结构稳定性。E-mail:wangweixfl@163.cn
吴 梵(1962-),男,教授,博士生导师。研究方向:舰船结构强度。
