基于ANSYS的光伏组件晶体硅电池片应力分析
2016-12-16黎之奇杨非池
黎之奇,杨非池
(湖南大学 土木工程学院,湖南 长沙 410082)
基于ANSYS的光伏组件晶体硅电池片应力分析
黎之奇†,杨非池
(湖南大学 土木工程学院,湖南 长沙 410082)
以单晶硅标准组件为研究对象,考虑不同风压及EVA(Ethylene-Vinyl Acetate Copolymer)胶膜剪切模量的影响,由ANSYS建立不同组件参数下光伏组件层合板的有限元分析模型,将计算结果与理论结果进行了比较、分析.结果表明:1)应力分布的变化趋势与理论模型一致,即应力的变化是非线性的,最大应力发生在电池片中点,电池片的应力随着EVA胶膜剪切模量的增加而呈非线性增加;2)组件受风载作用而弯曲变形时,电池片、EVA胶层和TPT(Tedlar/PET/Tedlar)的组合层对组件的整体刚度影响较小,组件近似按面板中面弯曲.
光伏电池片;EVA胶膜;有限元分析;Von Mises等效应力
近年来光伏发电在我国得到快速发展.地面电站和建筑外附式光伏系统大多采用晶体硅光伏组件,其核心为晶体硅太阳电池.由于我国幅员辽阔,气候和自然环境差异很大,在一些冬季寒冷和风载较高地区安装的光伏系统,组件晶体硅电池片的应力较高,从而引起隐裂、碎片等电池片失效问题.
组件的风荷载研究已有一些文献报导,其方法是以实测风压、风洞实验和数值模拟研究组件表面的风荷载分布,作为组件强度设计的基础.光伏组件是由多层材料采用层压工艺制造的,组件在服役期间的荷载主要有温度变化产生的热应力和风荷载引起的应力.温度应力由各层材料的热胀系数差异而导致,风载则属于机械荷载.由于晶体硅电池片内埋于EVA胶层中,因此给电池片的应力测量及分析计算都带来困难,有限元法是计算电池片应力的有效方法之一.
目前对于电池片的热应力计算和由风载产生的应力计算[8]已取得一些进展,这些研究工作基于将电池层作为一整体薄层,而实际组件的电池片是离散分布的,各电池片之间无相互作用,电池片的荷载来自于其上下EVA胶层的剪切应变.文献[9]基于最小势能原理,通过将位移分量取为重三角级数形式导出了光伏组件晶体硅电池片位移场及应力场的级数解.
本文针对光伏组件的构造特点及电池片的受力形式,基于通用有限元分析软件进行参数化数值模拟建立相应有限元计算模型,计算了组件在不同风压及EVA胶膜剪切模量发生变化时晶体硅电池片的应力分布,计算结果与文献[9]的理论结果进行了比较分析,并对组件弯曲变形时的中性面变化进行了讨论,为在恶劣外部环境及风荷载较高地区光伏组件的设计提供了依据.
1 电池片应力计算模型
图1所示为单晶硅太阳能电池板封装结构示意图,组件可分为5层结构,由上至下依次为超白钢化玻璃面板层、EVA胶膜层、晶体硅电池片层、EVA胶膜层和TPT背膜层,其中电池片层为离散排布的晶体硅电池片,电池片内埋于EVA胶层中,片与片之间的距离约为3~5 mm,每相邻电池片间仅有2条宽约3 mm,厚约0.1 mm的金属片作为电气连接,由层压机在真空和高温加热条件下层压制成太阳能组件.

图1 太阳能电池板封装结构图Fig.1 Solar panel encapsulated structure
在光伏组件中,玻璃面板作为风荷载下的主要承载构件,组件受到外荷载作用而产生弯曲变形,使得EVA胶层发生剪切变形.电池片内部的荷载即由EVA胶层的剪应变所产生,其中面板玻璃的变形引起上层EVA胶层的剪应变,而下层EVA胶层的剪应变则来自于TPT背膜的变形.有限元计算过程分2步进行:1)计算组件整体受风载作用时的最大挠度发生点及相应的内力;2)计算组件最大挠度发生点处所对应电池片的应力.
组件的整体计算针对某屋顶太阳能光伏项目中尺寸为1 580 mm×808 mm的195 W单晶硅标准组件光伏组件,组件内部由72片125 mm×125 mm单晶硅电池串联.组件安装于图2所示的支承结构上,组件仅在长边方向上的4个点用卡扣与支撑结构连接,在荷载作用下由于铝框的变形而导致组件的整体挠度较大.
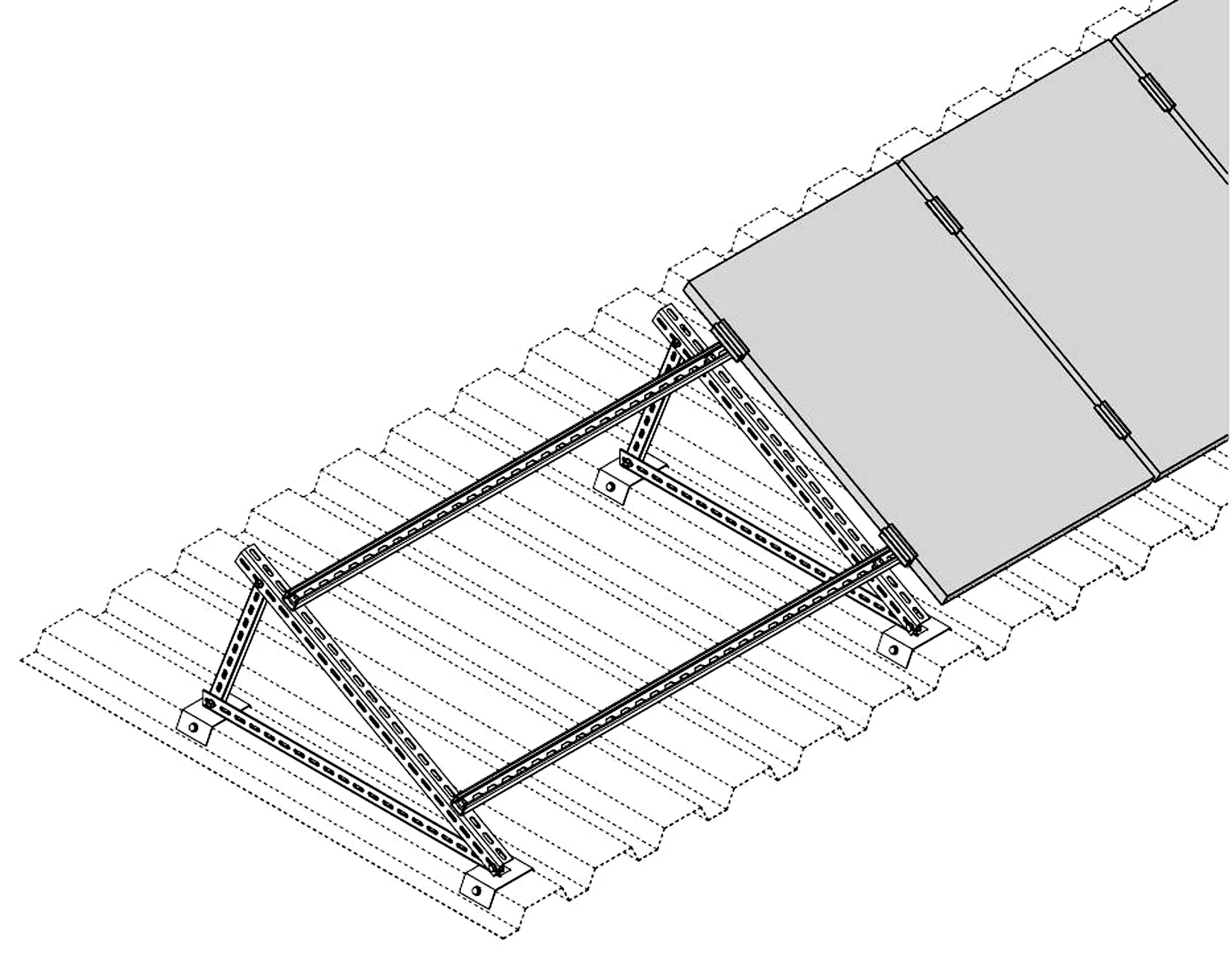
图2 光伏组件及支撑Fig.2 Photovoltaic modules and supports
利用有限元分析软件得到光伏组件在不同风荷载下组件的弯矩.计算时考虑了铝框的变形,结果表明5种风压下最大弯矩值均出现在组件中点处,最大弯矩值见表1,计算时取x轴沿组件短边方向,y轴沿组件长边方向.
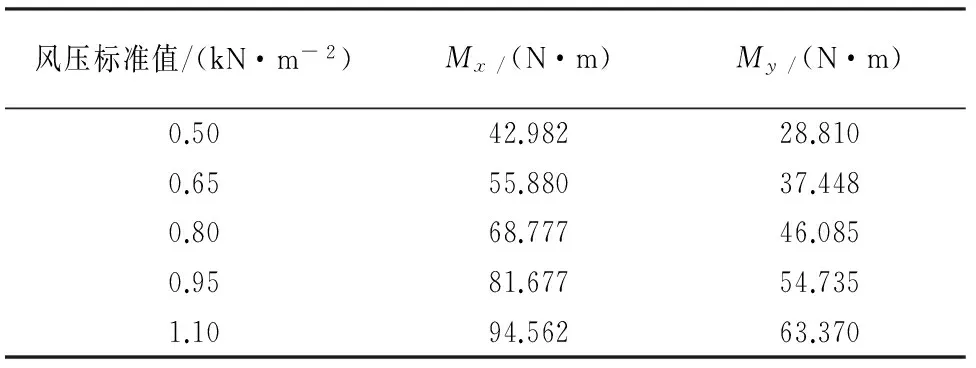
表1 面板玻璃中点处的弯矩值Tab.1 The bending moments at the middle of the panel
由于电池片是离散地分布于组件中,计算电池片的应力采用了如下方法:
1)在组件中点处取出仅包含一片电池的层合板计算单元,考虑到组件电池片间距为3~5 mm,因此计算单元取为129 mm×129 mm,包含一片125 mm×125 mm电池片,如图3(a)所示,坐标系取为x轴沿光伏组件短边方向,y轴沿光伏组件长边方向.
2)电池片尺寸与玻璃面板尺寸相差一个数量级以上,因此近似认为在计算单元范围内组件的弯矩为均布,如图3(b)所示.
3)均布弯矩Mx和My施加于面板、上下EVA胶层和TPT背膜上,但不施加于电池片上,电池片的荷载完全来自于上下EVA胶层的剪切变形.
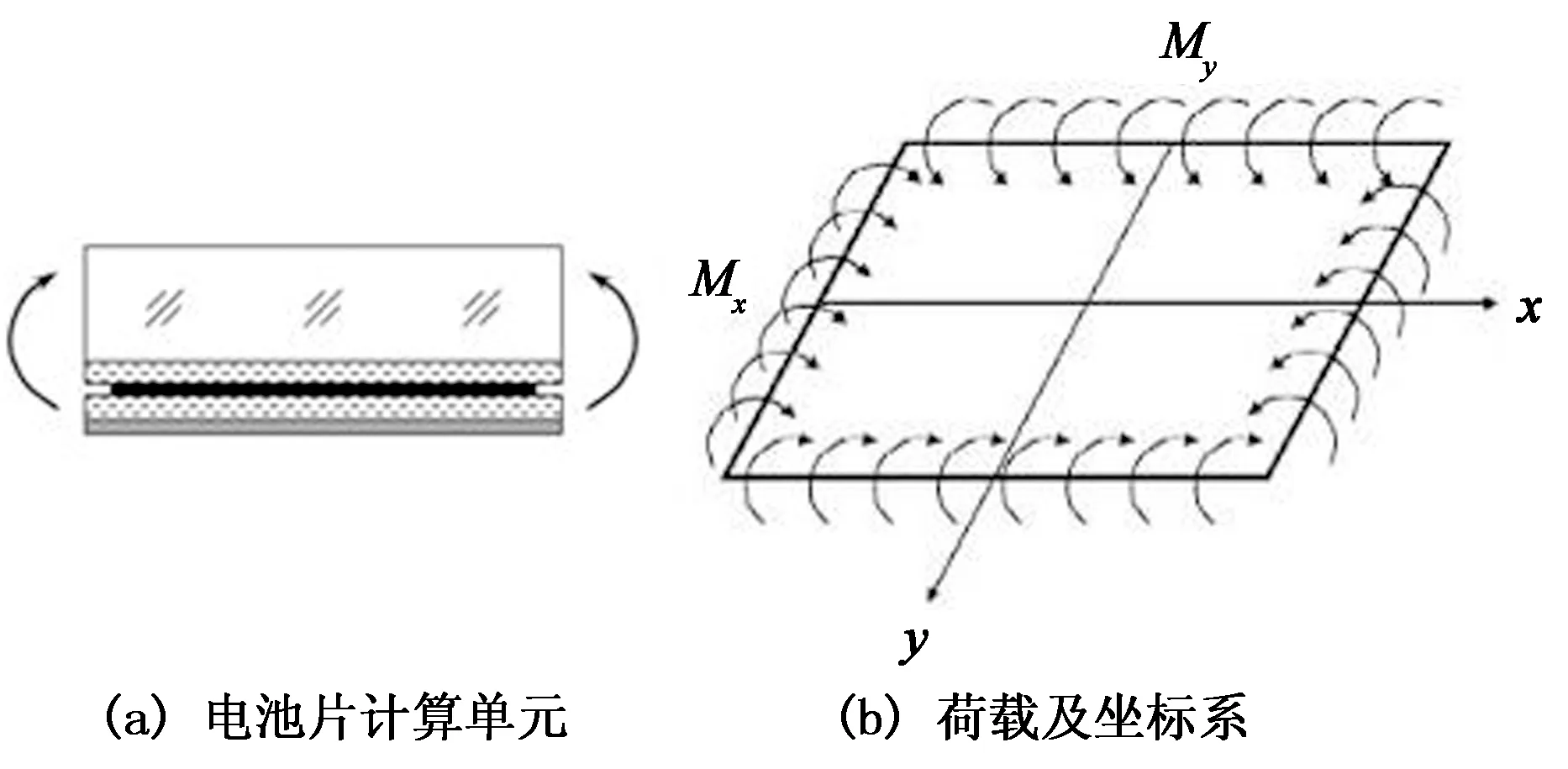
图3 电池片应力计算示意图Fig.3 Schematic diagram of the stress calculation of the photovoltaic cell
2 计算单元及材料参数
计算单元由5层材料构成,其中面板玻璃、电池片和TPT背膜的材料参数见表2,其中E为杨氏模量,t为各层厚度,ν为泊松比.

表2 材料参数Tab.2 Material parameters
用于太阳能电池封装的EVA胶膜,是采用质量分数为30%~33%的乙酸乙烯,并辅以数种改性剂,经成膜设备轧制成的薄膜状产品,属于乙烯和醋酸乙烯酯的共聚物,具有较高的透光率和抗老化能力.
EVA胶属于黏弹性材料,其储能剪切刚度GEVA随温度变化如图4所示[10],有3个典型区域,即:玻璃态区(T≤-40 ℃)、转变区(-40 ℃
3 有限元建模
本文使用ANSYS 14.5,通过参数化设计语言APDL将分析模型中变量分别定义为参数编写宏文件,进行参数化建模,并完成加载、求解、参数化提取结果.
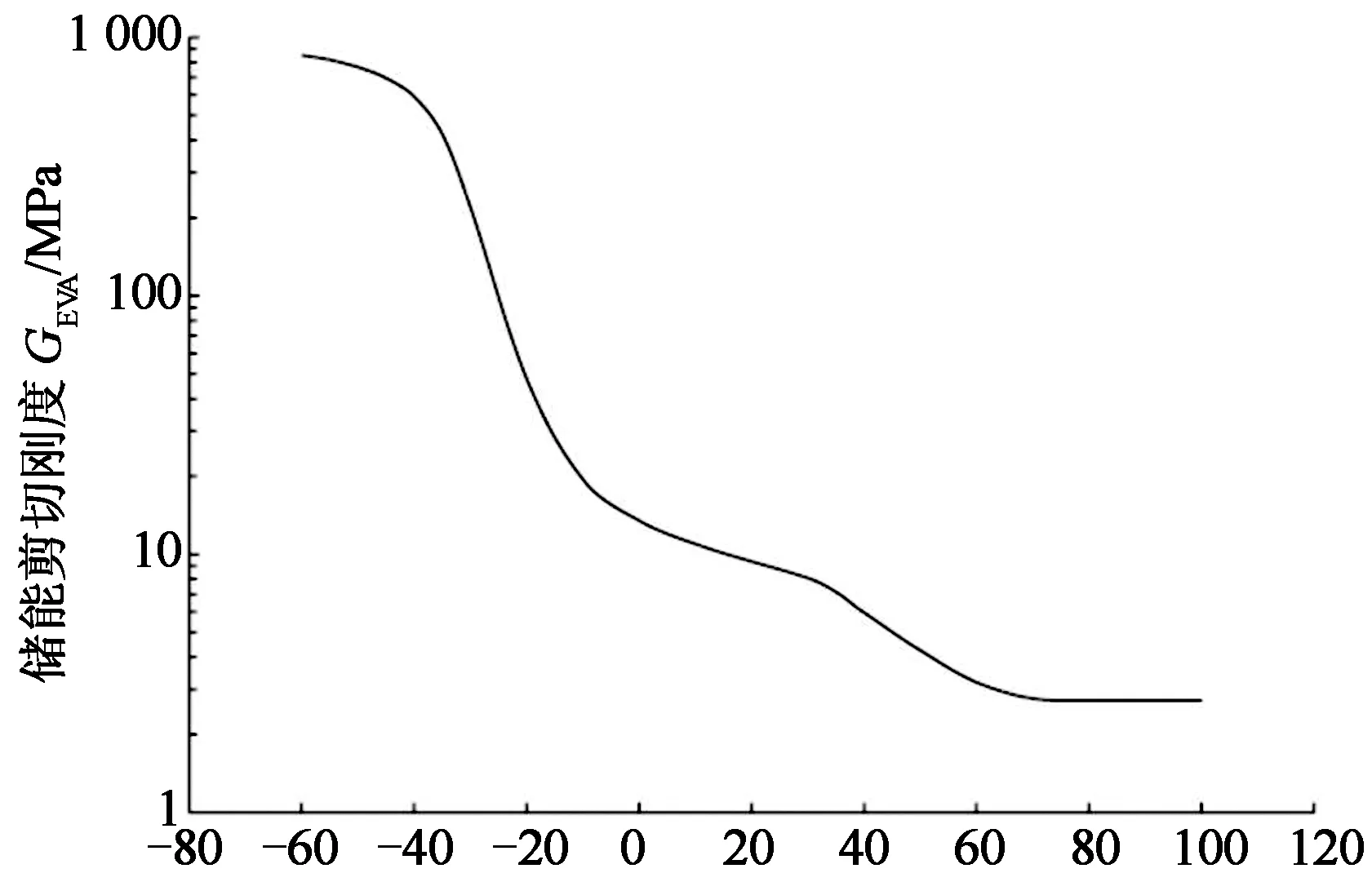
温度/℃图4 组件EVA胶的储能剪切刚度随温度的变化关系Fig.4 The relationship between shear storage modules of EVA and temperature
为简化起见,计算单元各层材料均视为各向同性材料,选用SOLID185单元进行模拟.EVA为黏弹性材料,其弹性常数是温度的函数,计算中将EVA胶膜的泊松比取为0.3,其他材料的力学性能参数见表2.
网格的划分:组件电池片部分凹进,模型为非规整的六面体,网格划分前先利用工作平面对实体模型进行切割,将层合板切割成规整的六面体进行映射网格划分.
约束的施加:由于SOLID单元没有转动自由度,弯矩的施加用到创建刚性区命令.将有转动自由度的MASS21单元作为主节点,与模型侧面对应的刚性区上从节点相连.在主节点上施加表1中的弯矩Mx和My,将弯矩施加到从节点上,建立约束方程.并在x=0及y=0的对称面上分别施加x方向及y方向的节点约束.
4 计算结果与分析
4.1 电池片应力
图5为储能剪切刚度GEVA分别取值为10, 20, 40 MPa,风压值为0.65 kN/m2时电池片的Von Mises应力分布云图.应力最大值发生在电池片中点处,然后向四周逐渐递减.在电池片角点处的应力为最小值.
文献[9]基于最小势能原理导出了光伏组件晶体硅电池片位移场及应力场的级数解,本文计算了GEVA= 10 MPa,风压值为0.65 kN/m2时电池片沿x轴及y轴上的等效应力,并与文献[9]的结果进行比较, 如图6所示.
图6的结果表明,电池片等效应力的最大值均出现在电池片中点处,沿x轴、y轴两端方向按非线性趋势减小,与文献[9]一致.在电池片边缘处文献[9]的应力为零,与本文结果有较大差异.
分析造成误差的原因有:文献[9]采用的解答是在最小势能原理下的近似解,而位移表达式采用重三角级数时,满足位移边界条件和应力边界的解在边界上各正应力分量均为零.由于电池片处于双向拉伸状态,边界上的正应力分量不全为零,因此本文的计算结果更为合理.
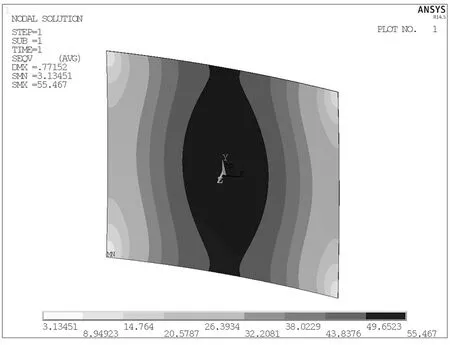
(a)GEVA = 10 MPa

(b)GEVA = 20 MPa
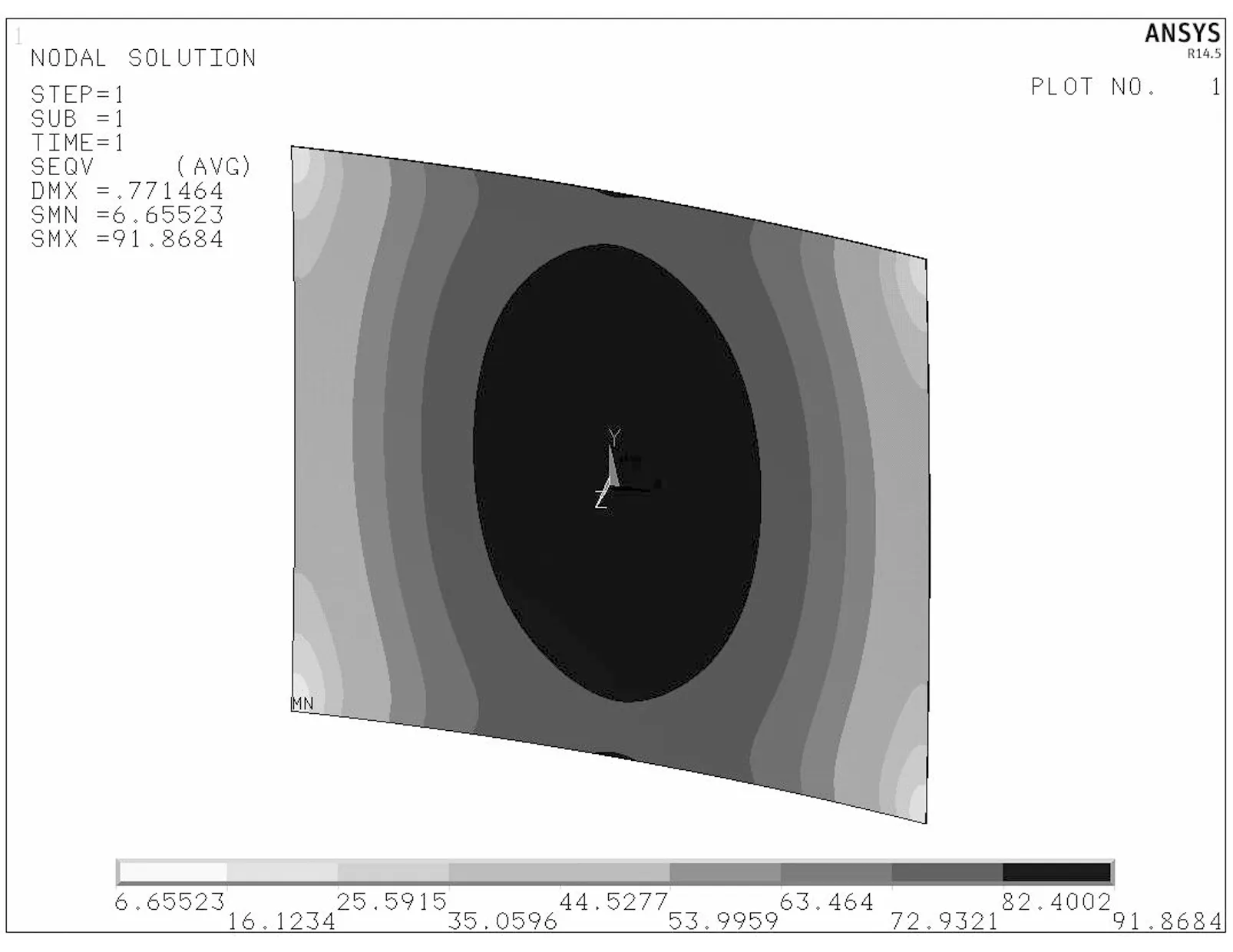
(c)G'EVA = 40 MPa图5 应力云图Fig.5 Stress contour figures
在表1所示的风压下,计算了电池片中点处最大应力随EVA胶膜储能剪切刚度的变化曲线,如图7所示.结果表明,文献[9]的计算结果比本文分析结果整体偏小,偏差在15%以内.
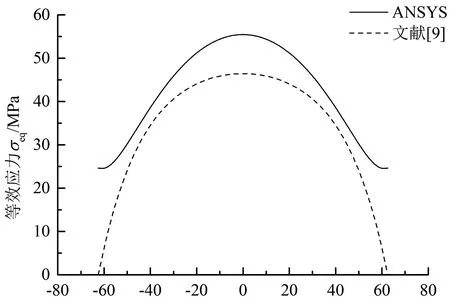
x/mm (a) 沿x轴
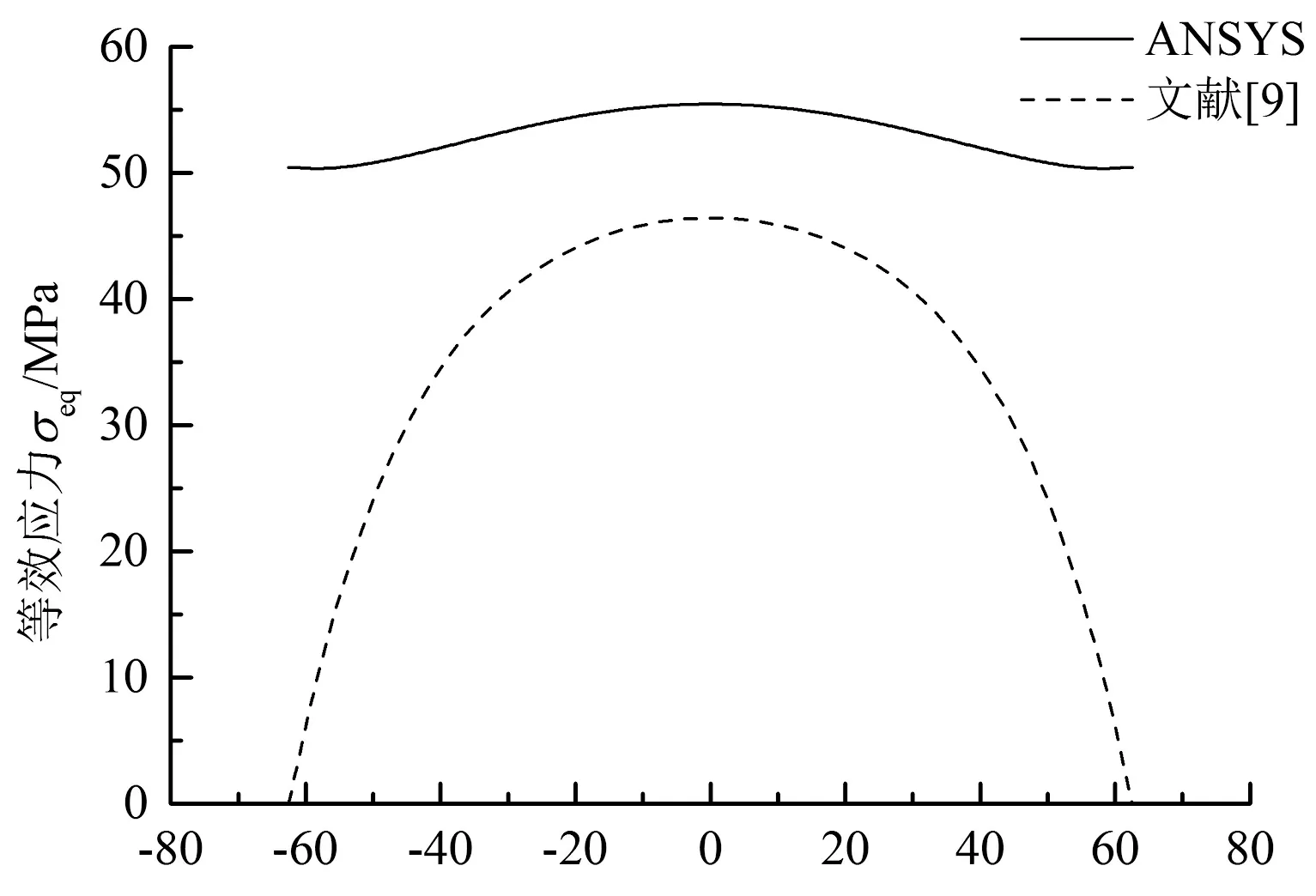
y/mm (b) 沿y轴图6 电池片等效应力的变化Fig.6 The variation of the Von Mises stress in cell
4.2 组件弯曲中性面分析
光伏组件是多层结构,受风载作用弯曲变形时,其弯曲中性面将偏离面板玻璃的中性面,文献[9]基于EVA胶膜弹性模量比玻璃面板的弹性模量低3个数量级,TPT背膜的弹性模量比玻璃面板的弹性模量低2个数量级,且电池片的分布是离散的,认为EVA胶膜、电池片和TPT背膜的组合层对组件的整体刚度影响较小,提出组件近似按面板玻璃自身的中性面弯曲变形,从而简化了电池片力学分析模型.
以本文方法计算了储能剪切刚度GEVA分别为10, 20, 40 MPa时组件中性面与玻璃面板中性面的偏离值如图8(a)(b)所示,结果表明最大偏离值均出现在电池片中点所对应的位置.
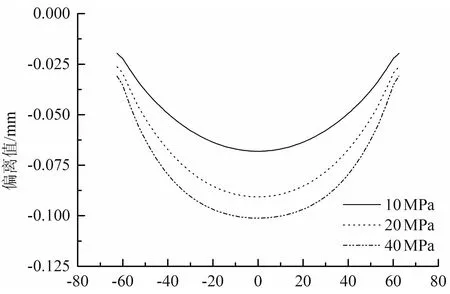
y/mm (b)沿y轴
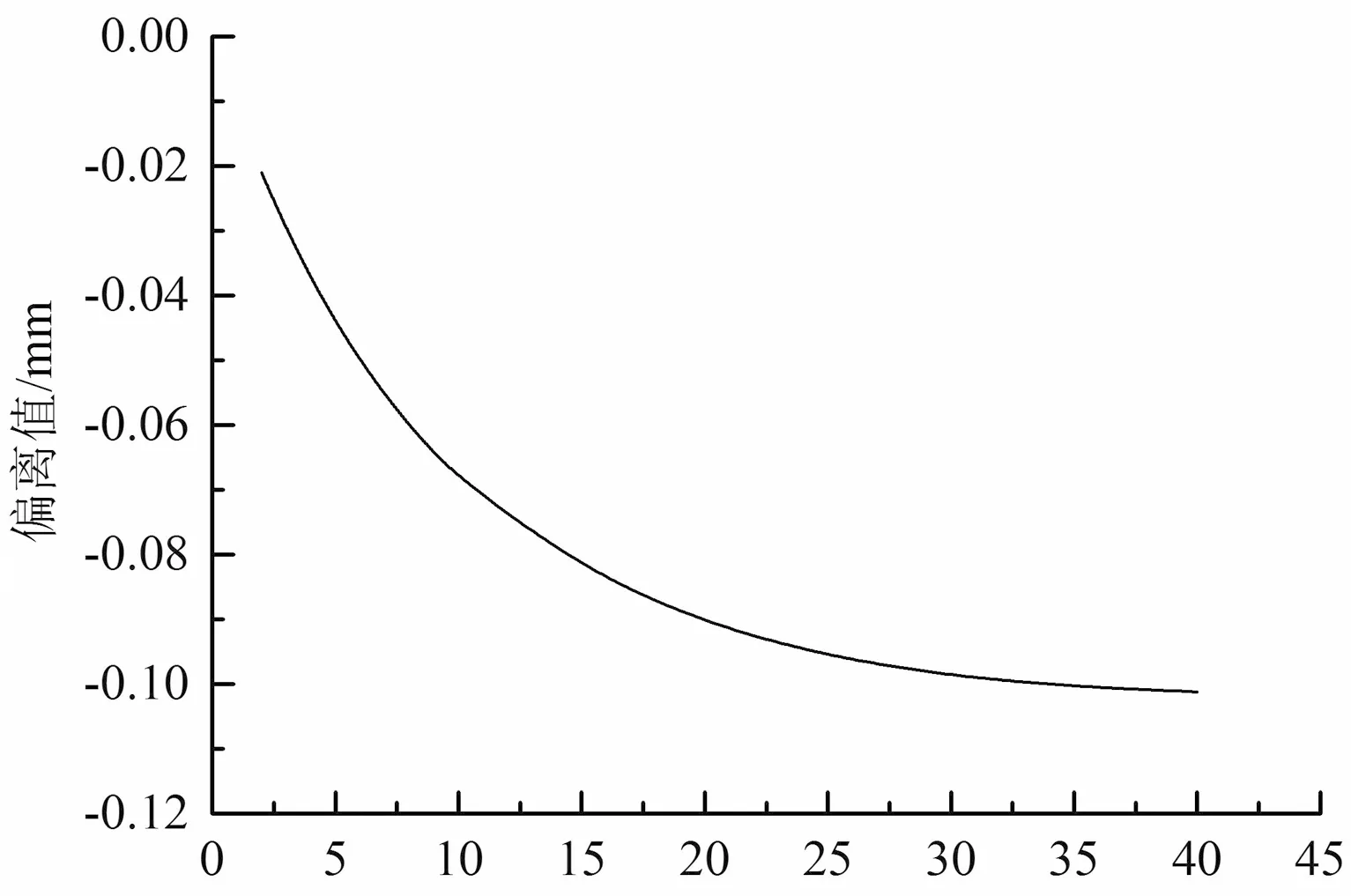
GEVA/MPa (c)中点处最大偏移值图8 中性面偏离值Fig.8 The deviation of neutral plane
图8表明组件中性面的偏离随GEVA的增加而增大,因此计算了GEVA由2 MPa变化至40 MPa时中点处的偏离值,如图8(c)所示.可以看到,随着胶膜剪切模量的增大,中性面最大偏移值呈非线性增大,GEVA=40 MPa时的最大偏离值为0.101 mm,远小于面板厚度(3.2 mm),因此文献[9]的假设是合理的.
5 结 论
1)针对光伏组件的构造特点,建立了晶体硅电池片的力学计算模型.
2)与文献[9]基于最小势能原理的重三角级数解进行比较,结果表明,二者的最大应力都出现在电池片中点.在电池片边缘处文献[9]的Von Mises等效应力为零,与实际不符,而本文结果更为合理.
3)计算结果表明,受风载作用时组件的弯曲中性面与玻璃面板自身中性面的偏离值远小于面板玻璃厚度,因而在理论分析和计算时可以近似认为组件以面板自身中性面弯曲变形,从而简化了层合板的应力分析模型.
4)在温度较低时,EVA胶膜的剪切刚度增大,风压在电池片内引起的应力较高,容易引起隐裂、碎片等电池片失效问题,因此在冬季寒冷的地区应用光伏时应充分考虑风荷载的影响.
[1] JUBAYER C, HANGAN H. Numerical simulation of wind loading on photovoltaic panels[C]//Proceedings of the 43rd Structures Congress. Chicago, Illinois: American Society of Civil Engineers, 2012: 1180-1189.
[2] 黄浩,吴志学.光伏组件变形对组件性能的影响研究[J].机械工程与自动化, 2011(4): 107-109.
HUANG Hao, WU Zhi-xue. Effect of PV modules deformation on component performance[J]. Mechanical Engineering & Automation, 2011(4):107-109.(In Chinese)
[3] COSOIU C I, DAMIAN A, DAMIAN R M,etal. Numerical and experimental investigation of wind induced pressure on photovoltaic solar panel[C]//Proceedings of the 4th IASME/WSEAS International Conference on Energy, Environment, Ecosystems and Sustainable Development. Algarve, Portugal: WSEAS, 2008: 11-13.
[4] 王晓燕, 耿洪滨, 何世禹, 等. 热循环下太阳电池板单元结构热应力演变规律研究[J]. 太阳能学报, 2007,28(4):345-350.
WANG Xiao-yan, GENG Hong-bin, HE Shi-yu,etal. Thermal stress study of solar PV module structure[J]. Acta Energiae Solaris Sinica, 2007,28(4):345-350. (In Chinese)
[5] 王晓燕, 耿洪滨, 何世禹, 等. 热循环作用下太阳电池板单元结构寿命预测[J]. 太阳能学报, 2007,28(6):583-586.
WANG Xiao-yan, GENG Hong-bin, HE Shi-yu,etal. Life forecast of element structure of solar panel under thermal cycles[J]. Acta Energiae Solaris Sinica,2007,28(6):583-586. (In Chinese)
[6] CAO M, BUTLER S, BENOIT J T,etal. Thermal stress analysis/life prediction of concentrating photovoltaic module[J]. Journal of Solar Energy Engineering, 2008,130:1-9.
[7] EITNER U, PANDER M, KAJARI-SCHRODER S,etal. Thermomechanics of PV modules including the viscoelasticity of EVA[C]//Proceedings of the 26th European Photovoltaic Solar Energy Conference. Hamberg, Germany: ETA-Renewable Energies and WIP-Renewable Energies ,2011: 3267-3269.
[8] 封忠江,晏石林,陈刚. 光伏组件机械载荷试验及数值模拟研究[J].固体力学学报, 2014,35(S1):251-255.
FENG Zhong-jiang, YAN Shi-lin, CHEN Gang. Mechanical load experiments on PC module and its numerical simulation[J]. Chinese Journal of Solid Mechanics, 2014, 35(S1):251-255. (In Chinese)
[9] 黎之奇. 光伏组件晶体硅电池片应力分析[J]. 太阳能学报, 2015,36(6):1493-1498.
LI Zhi-qi. Stress analysis of crystalline silicon solar cell in PV module[J]. Acta Energiae Solaris Sinica, 2015,36(6):1493-1498. (In Chinese)
[10]EITNER U, KAJARI-SCHRODER S, KONTGES M,etal. Non-linear mechanical properties of Ethylene-Vinyl Acetate (EVA) and its relevance to thermomechanics of photovoltaic modules[C]// Proceedings of the 25th European Photovoltaic Solar Energy Conference. Valencia, Spain:ETA-Renewable Energies and WIP-Renewable Energies,2010: 6-10.
Stress Analysis of Crystalline Cell in PV Modules Using ANSYS
LI Zhi-qi†,YANG Fei-chi
(College of Civil Engineering, Hunan Univ, Changsha, Hunan 410082, China )
A finite element model of the photovoltaic module with different component parameters was established and Von Mises stress of crystalline cell was calculated using ANSYS software. The effects of wind pressure and shear modulus variation of EVA were taken into account in the analysis. The analysis results show that 1) the stress distribution in the cell agrees with the theoretical results(i.e., the maximum stress occurs at the center of the cell and the stress decreases nonlinearly toward the cell edges, and the stress in the cell increases nonlinearly with an increase of shear modulus of EVA); and 2) the composite layer that consists of EVA, cells, and TPT exhibits a little effect on the rigidity of the module, when it is subjected to wind loads and flexural deformation occurs approximately at the neutral surface of the panel.
photovoltaic cell; EVA; finite element analysis; Von Mises stress
1674-2974(2016)11-0149-05
2015-07-24
黎之奇(1963-),男,湖南长沙人,湖南大学教授,博士†通讯联系人,E-mail:zqlee@hnu.edu.cn
TU18
A
