基于正交试验的寒区隧道温度场影响因素敏感度研究

2016-12-16周小涵曾艳华周晓军阮亮红魏英杰

湖南大学学报（自然科学版） 2016年11期

周小涵，曾艳华，范磊，周晓军，阮亮红，魏英杰

(1．西南交通大学交通隧道工程教育部重点实验室，四川成都 610031；2．中铁二院工程集团有限责任公司土建一院隧道所，四川成都 610031；3．中铁大桥勘测设计院集团有限公司，湖北武汉 430050；4．成都建筑工程集团总公司，四川成都 610014)

周小涵1，3，曾艳华1†，范磊2，周晓军1，阮亮红1，魏英杰4

影响寒区隧道温度场的因素众多，建立基于有限差分的隧道非稳态传热计算模型，以实际寒区铁路隧道南山隧道为例，采用正交试验法分别以隧道衬砌内部节点平均温度、隧道某断面衬砌温度和隧道洞口纵向冻结长度为指标对影响隧道温度场的各因素进行敏感度研究.结果表明：不同指标下各因素敏感度排列有局部差异；总体来讲，隧道埋深、洞内风向、隧道断面大小、洞内风速、入口风温、围岩导热系数、隧道埋深是影响隧道温度场的主要因素，围岩比热容、围岩密度是影响隧道温度场的次要因素.在寒区隧道抗防冻设计中，除去围岩比热容、围岩密度、围岩导热系数、入口风温等不可更改因素，对隧道温度场影响较大的隧道埋深、洞内风向、洞内风速、隧道断面大小、隧道埋深等隧道设计参数必须合理设置.

寒区铁路隧道；温度场；正交试验；敏感度分析

国内外关于隧道温度场计算方法有了很多研究，例如：Pande等[1](1984)推导了两相介质的整合热传导率取值方法；Okadak[2](1985)提出了寒区隧道隔热层的设计方法；Dr. Meissner M等[3](1993)讨论了有序和无序固体介质的热传导问题；Toutain J等[4](2011)进行了传热模型的拉普拉斯变换反演；夏才初等[5-6](2010)考虑衬砌和隔热层的影响，推导了包含隧道内气流的温度场解析解.然而，虽然某些论文中有对单个计算参数的定性研究，但是对隧道温度场计算模型的各个参数的全局敏感度还没有进行过系统的研究.

对于计算模型中各计算参数的敏感度研究，众多学者应用正交试验法进行了分析，这些计算模型影响因素包括：徐超等[7](2004)计算深基坑重力式挡土墙侧向变形的岩土参数[7]；计算连续刚构桥地震响应的桥梁跨数和墩高、行波波速、桩土作用、地震波类型等参数[8]；计算边坡稳定的滑带土力学参数[9];计算聚集物燃烧时极限温度值的聚集物的厚度、通风风速、聚集物燃点和风管断面尺寸等参数[10];影响采场采场稳定性的结构参数[11]；计算混凝土面板堆石坝竖向位移、上下游水平位移的邓肯-张E-B模型参数[12]；相似模拟试验中的低强度相似材料参数包括铁矿粉、重晶石粉、砂及石膏用量[13].可见，应用正交试验法研究模型计算参数敏感度的方法较为成熟.

本文以寒区铁路隧道为例，建立隧道温度场非稳态有限差分计算模型，可以计算考虑洞口风温、洞内风速、隧道埋深、隧道断面大小等因素的隧道温度场.然后，以隧道衬砌平均温度、某横断面断面衬砌温度和隧道入口端纵向冻结长度为指标，采用基于正交试验的全局敏感度分析法着重研究影响温度场的各个因素包括入口风温、洞内风向、洞内风速、隧道断面大小、隧道埋深、围岩导热系数、围岩比热容、围岩密度等的全局敏感度.通过研究，提出影响寒区隧道抗防冻设计的主要影响因素，为其设计和研究提供指导.

1 非稳态温度场计算模型

由于热辐射相对较小，故本模型只计对流换热和热传导作用.计算模型假定隧道横断面为圆形，以隧道的等效水力半径R作为计算模型的半径.为了模型计算的实现，假定围岩和每一种衬砌为独立的为各向同性、均匀的连续介质.计算初始，假定衬砌温度等于围岩原温，围岩原温沿径向不变.

根据傅里叶导热定律、能量守恒定律，得出导热偏微分方程.隧道纵向瞬态温度场围岩部分的控制方程[5]可以表示为(柱坐标系下):

(1)

边界条件为：

t(r,x,τ)=tw(r≥R,τ=0)

(2)

(3)

将隧道内气流视为无粘性不可压缩的稳定流体，根据隧道内纵向气流的质量守恒、动量守恒、能量守恒定律[14-15]，推导隧道纵向瞬态温度场气流部分的控制方程为：

(4)

边界条件为:

tf(x,τ)=tb(τ=0)

(5)

式中t是衬砌或围岩内部任一点温度；r是衬砌或围岩中任一点到隧道中心的距离；τ是时间参数；ρ是空气密度；a为围岩的导温系数；cp是空气的比热容；tf是风流温度；tb是隧道壁面温度；tw是围岩温度；h是对流换热系数；U是隧道断面周长；qs是隧道内发热设备的均匀发热量；v是风流速度.

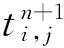
(6)

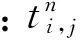
(7)

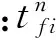
(8)

式中：Δra为介质a的距离步长；Δrb为介质b的距离步长;节点(i,j-1)向节点(i,j)传热量为Qj-1-j；节点(i,j+1)向节点(i,j)传热量为Qj+1-j；节点(i-1,j)向节点(i,j)传热量为Qi-1-i；节点(i+1,j)向节点(i,j)传热量为Qi+1-i；θ是绝热边界的夹角.

(9)

式(6)～式(9)所表述的隧道温度场计算模型在文献[14]中通过CFD软件验证了其准确性，在此不再赘述.

考虑寒区铁路隧道特点，根据隧道非稳态温度计算模型的计算参数，排除影响较小的因素，提出全局敏感度考察因素有：洞口风温、洞内风向、洞内风速、隧道断面大小、对流换热系数、隧道埋深、围岩导热系数、围岩比热容、围岩密度及影响隧道原始温度的隧道埋深等共9个影响因素.根据实验风流流速与对流换热系数的关系[16]可知，隧道内风流流速和对流换热系数基本呈线性关系，所以风速的敏感度水平也代表了对流换热系数的敏感度水平.故这里将两个因素综合考虑，以风速的敏感度代表风速和对流换热系数的整体敏感度，这样，影响因素变为8个.

由于寒区隧道温度场问题是一个含相变的问题，围岩导热系数、围岩比热容等参数在冻结区和非冻结区的取值不同，常见的处理方式是假设相变发生在相变温度附近的一个温度范围内，而构造不同温度区域内导热系数和比热容的取值函数[5，17]．而由于本文的研究是定性地分析隧道温度场影响因素的敏感度，为了研究的可行性，在计算中假定各热物理参数为恒定值.

2 寒区隧道模型

选取东北寒区南山隧道展开研究，隧道纵断面图如图1所示.

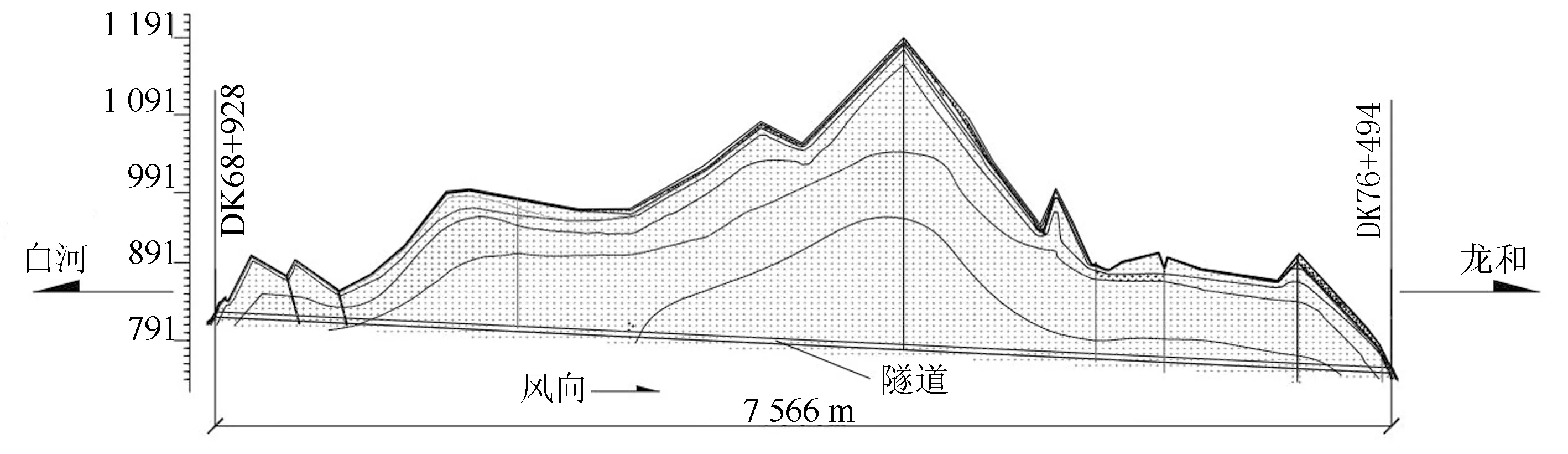
图1 南山隧道纵断面图Fig.1 Longitudinal section of Nan Shan tunnel

南山隧道沿线属于中温带湿润大陆性季风气候区，冬季漫长而严寒多雪，夏季凉爽并低温多雨，雨季在6～7月份.沿线历年最冷月平均气温-12.1～-12.69 ℃，属寒冷地区.隧道全长7 566 m，最大埋深385 m，隧道当量直径D=5.96 m.由于缺少隧道贯通时的洞内围岩温度资料，本文采用隧道温度场计算中常见的地温梯度法[18]，参考地表地温分布规律和南山隧道当地气温条件，取变温层深度为30 m，恒温层深度为25 m，增温层的温度梯度3 ℃/100 m[17，19]，根据隧道埋深，计算得到各隧道沿纵向的原始地温.

根据工程地质勘查资料和气候资料，材料基准计算参数如表1所示，参考实测洞内风速[16]，对流换热系数取为17 W/(m2·k).

表1 介质材料基准参数Tab．1 Basic parameters of dielectric materials

3 正交试验敏感度分析

3.1 正交试验原理

正交试验方法是根据数理统计学与正交性原理，从大量试验中选取有代表性的试验，按照 “正交表” 安排试验.正交表具有 “整齐可比性” 和 “均衡分散性” 的特点，因此，通过正交试验设计, 既可大大减少试验次数,又可以达到全面试验分析的目的,即找出各因素对试验考核指标(即试验观测数据)的影响规律[7].

用正交试验法分析各指标敏感度的大致步骤为:1)确定全局敏感性分析的各因素和试验指标；2)确定变化因素的数量及各因素变化的水平数，选择正交试验表；3)按正交表的要求列出试验方案表，计算各方案的指标值；4)总结各因素水平的平均计算值，计算极差R，按极差大小对各因素敏感性进行排序.

3.2 试验指标与正交表的选取

寒区隧道抗防冻设计关注的焦点是洞内衬砌和周边围岩的温度是否达到冻结温度以下，包括冻结区的纵向范围及局部丰富藏水段的温度分布等.所以，以隧道初衬沿纵向全长的平均温度、某局部断面(距小里程洞口3 000 m)处衬砌温度和隧道小里程入口端纵向冻结长度(<0 ℃)为计算指标展开正交试验.

试验中，自然风风向以自小里程向大里程吹和自大里程向小里程吹两个方向进行研究，即风向为正或为负两水平，假定风向改变时，隧道入口风温不变.其余各因素以在基础参数值基础上以-20%，0，+20% 3个水平进行研究.基准参数取值为，某月实测平均洞门风温-17 ℃，某月实测洞内风速平均值2.5 m/s，隧道断面当量直径5.96 m，其他参数见表1.计算最冷月平均气温-17 ℃连续作用30 d后隧道的温度场.隧道埋深直接影响隧道原始温度场，假定隧道平均埋深分别增加20%、不变和减少20%，计算其对应原始温度场并带入模型进行分析.

根据影响因素数量和变化水平，选用L18(21×37)正交表进行分析，正交表设计如表2所示.

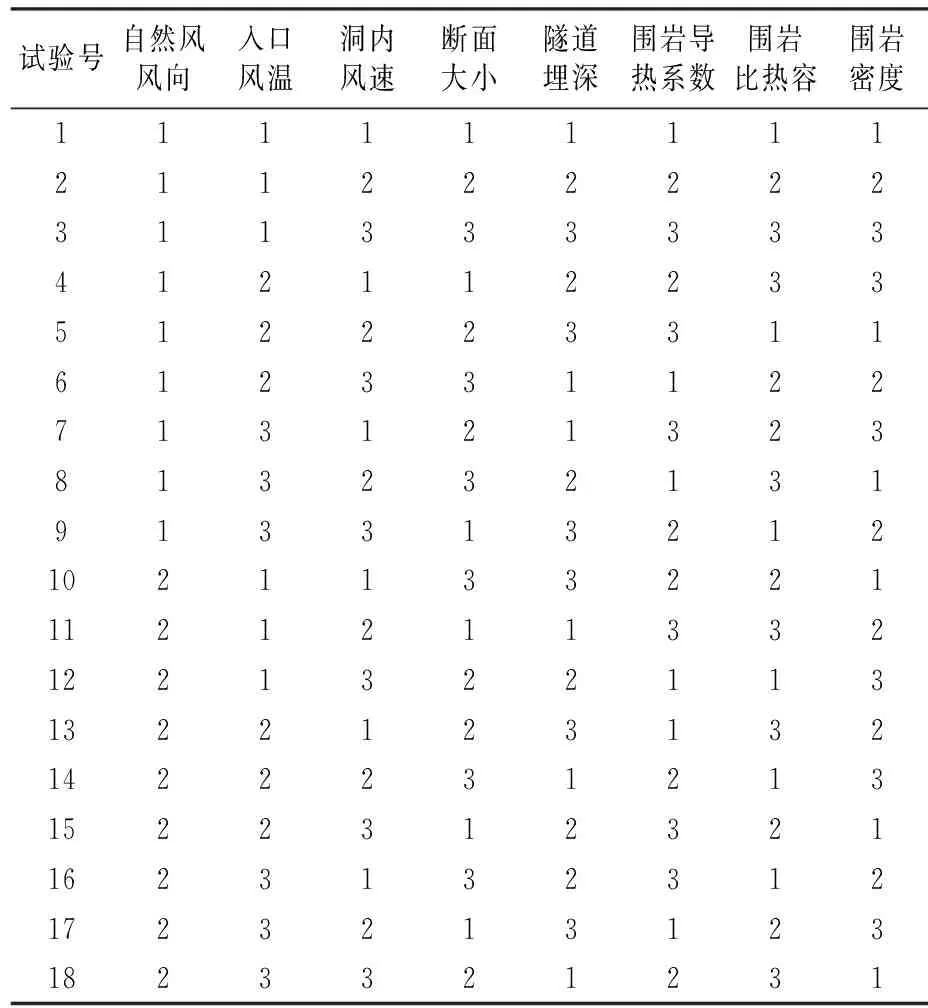
表2 L18(21×37)正交试验表Tab．2 L18(21×37)orthogonal table

3.3 试验结果分析

通过L18(21×37)正交表分析各影响因素对隧道温度场的影响程度.由于洞内风向只有两个水平，1～9号试验和10～18号试验两组试验各自的风向都是相同的，同时其他因素均出现相同的次数，可以认为2组试验结果的差异是由风向的变化引起的.对于风向以外的其他影响因素，如入口风温，分别取3个水平的6次试验结果平均值作为每组的试验结果，则3组试验结果的差值即可反映入口风温变化时对隧道温度场的影响程度.把每个影响因素3组试验结果最大差值作为极差，以极差的大小来判定各影响因素对隧道温度场的影响大小，即各影响因素的灵敏度.

计算以最冷月份平均入口风温-17 ℃连续作用30 d后的隧道温度场，各个指标的影响因素敏感度如表3～表5所示.

表3 距小里程洞口3 000 m处横断面初衬温度正交试验极差计算表Tab．3 Orthogonal test range calculation of cross-sectional lining temperature 3 000 m away from the tunnel entrance

表4 隧道初衬纵向全长的平均温度正交试验极差计算表Tab．4 Orthogonal test range calculation of average lining temperature

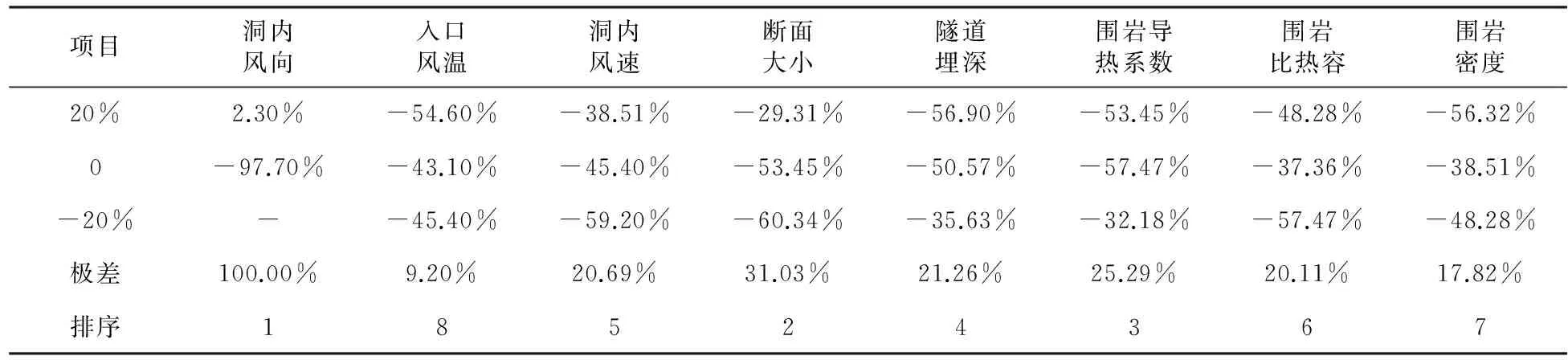
表5 隧道入口段冻结纵向长度正交试验极差计算表Tab．5 Orthogonal test range calculation of the freezing length of tunnel entrance

由表3可知，距小里程洞口3 000 m处横断面初衬温度正交试验结果表明，隧道埋深的极差为0.955 8，是最敏感的因素.洞内风向极差为0.884 8，是仅次于埋深的因素.由于自然风风向的水平以方向表示，其他因素的水平以量化的数值来表示，因此，洞内风向不宜与其他因素直接进行比较，但是自然风风向直接影响了隧道两端洞口段温度场的分布差异及洞内局部断面的温度，在研究隧道温度场时不可忽略.各影响因素的敏感度排序依次为隧道埋深(0.955 8)、洞内风向(0.884 8)、断面大小(0.828 2)、洞内风速(0.654 6)、入口风温(0.244 9)、围岩导热系数(0.177 2)、围岩密度(0.069)和围岩比热容(0.042 4).

由表4可知，洞内风向对于隧道初衬纵向全长的平均温度的影响很小.分析试验结果发现，对于每个试验节点来说，风向的改变对于温度的影响是很大的，由于纵向节点平均温度是取多个节点的试验温度平均值，分析时综合其变化，因此出现了自然风风向极差很小的现象.各影响因素的敏感度排序依次为隧道埋深(1.084 9)、断面大小(0.940 2)、洞内风速(0.555 3)、入口风温(0.453 0)、围岩导热系数(0.266 5)、围岩比热容(0.166 9)、围岩密度(0.081 4)、洞内风向(0.010 1).

由表5可知，洞内风向对于隧道入口段冻结纵向长度正交试验结果的影响最大，各影响因素的敏感度排序依次为洞内风向(1.000)、断面大小(0.310 3)、围岩导热系数(0.252 9)、隧道埋深(0.212 6)、洞内风速(0.206 9)、围岩比热容(0.201 1)、围岩密度(0.178 2)、入口风温(0.092 0).

为了更为直观地表达各因素的敏感度，将不同指标时隧道温度场计算模型影响因素敏感度的柱状图列出如图2所示.

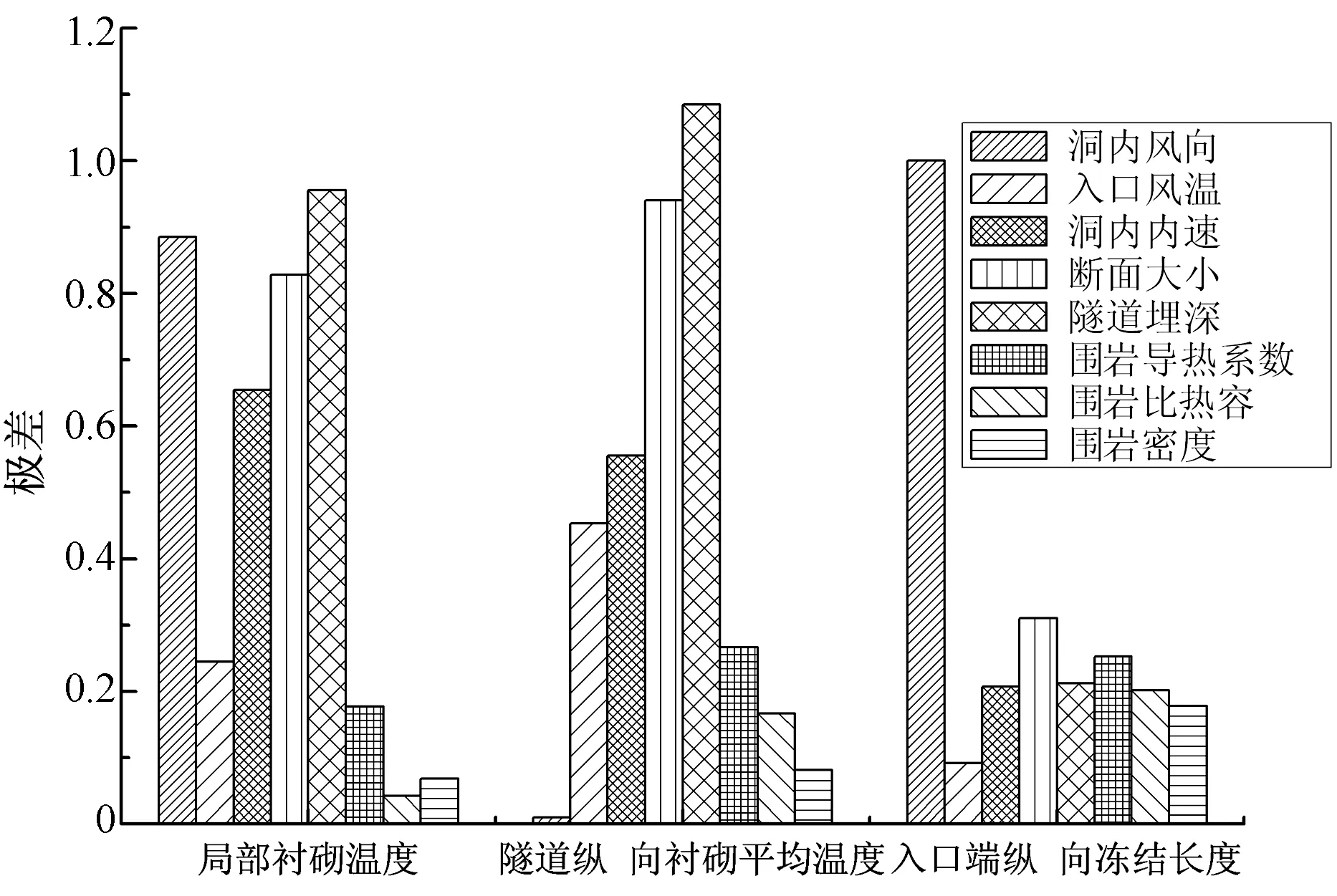
温度场影响因素图2 不同指标时隧道温度场计算模型影响因素敏感度对比Fig.2 Comparison of influence factor sensitivity on tunnel temperature field calculation model with different parameters

总地来说：隧道埋深影响隧道的原始岩温，对开挖运营后的隧道温度场影响显著；两水平的洞内风向直接影响了隧道两端洞口段温度场的分布差异及洞内局部断面的温度；隧道断面为气流和围岩的热交换提供了空间，断面越大，单位时间内热交换量越大；入口风温和洞内风速表证了冷空气吸入量，大的风速和低的风温直接加速洞内气流温度的降低，提高对流换热速率；围岩导热系数表征了围岩热传导的快慢，对温度场有重要影响.所以，隧道埋深、洞内风向、隧道断面大小、洞内风速、入口风温、围岩导热系数是影响隧道温度场的主要因素，而影响较小的围岩比热容和围岩密度是次要因素.

在寒区隧道抗防冻设计中，围岩比热容、围岩密度、围岩导热系数、入口风温等因素为不可更改因素.隧道埋深、断面大小、洞内风速、洞内风向等是可以调控的隧道抗防冻设计参数，而它们又都是对寒区隧道温度场影响较大的因素，所以必须引起足够的重视.

4 结论

应用基于有限差分的隧道非稳态传热模型和正交试验法，对寒区隧道洞口风温等8个影响因素进行了在以隧道某横断面初衬温度、初衬纵向平均温度、入口端冻结长度等为指标时的敏感度分析.得出结论如下：

1)当以不同指标进行正交实验时，各影响因素的敏感度排列有局部差异，主要由于指标的关注角度不同所致.总地来讲，隧道埋深、洞内风向、隧道断面大小、洞内风速、入口风温、围岩导热系数是影响隧道温度场的主要因素，围岩比热容、围岩密度是影响隧道温度场的次要因素.

2)在寒区隧道抗防冻设计中，除去围岩比热容、围岩密度、围岩导热系数、入口风温等不可更改因素，对隧道温度场影响较大的隧道埋深、洞内风向、洞内风速、隧道断面大小等抗防冻设计参数需合理设置.

3)本文计算模型可以计算考虑洞口风温、洞内风速、隧道埋深、断面大小等因素的隧道温度场，研究结果对南山隧道工程有指导意义，方法可供类似隧道参考.

[1] PANDE R N, KUMAR V, CHAUDHARY D R. Thermal conduction in a homogeneous two-phase system[J]. Pramana, 1984, 22(1): 63-70.

[2] OKADA K. Lcile prevention by adiatic treatment of tunnel lining [J]. Japanese Railway Engineering,1985, 3(26): 75-80.

[3] DR MEISSNER M, POHL P R O, KRUMHANSL J A. Phonon scattering in condensed matter VII[M]. Berlin:Springer Berlin Heidelberg，1993：3-8.

[4] TOUTAIN J, BATTAGLIA J L. Numerical inversion of laplace transform for time resolved thermal characterization experiment[J]. Journal of Heat Transfer，2011,133(4):44-54.

[5] 夏才初，张国柱，肖素光. 考虑衬砌和隔热层的寒区隧道温度场解析解[J]. 岩石力学与工程学报, 2010,29(9):1767-1773.

XIA Cai-chu, ZHANG Guo-zhu, XIAO Su-guang. Analytical solution to temperature fields of runnel in cold region considering lining and insulation layer[J]. Chinese Journal of Rock Mechanics and Engineering,2010, 29(9): 1767-1773.(In Chinese)

[6] 张国柱，夏才初，殷卓. 寒区隧道轴向及径向温度分布理论解[J]. 同济大学学报:自然科学版, 2010, 38(8): 1117-1122.

ZHANG Guo-zhu, XIA Cai-chu, YIN Zhuo. Analytical solution to axial and radial temperature of tunnel in cold region[J]. Journal of Tong Ji University :Nature Science, 2010, 38(8): 1117-1122.(In Chinese)

[7] 徐超，叶观宝. 应用正交试验设计进行数值模型参数的敏感性分析[J]. 水文地质工程地质, 2004, 31(1): 95-97.

XU Chao ,YE Guan-bao. Parameter sensitivity analysis of numerical model by cross test design technique [J]. Hydrogeology and Engineering Geology, 2004, 31(1): 95-97.

[8] 周勇军，全伟，贺拴海. 基于正交试验的连续刚构桥地震响应敏感性参数分析[J]. 地震研究, 2006, 29(2):176-181.

ZHOU Yong-jun，QUAN Wei,HE Shuan-hai. Analysis on sensitive parameters to earthquake response of continuous rigid frame bridges based on cross test technique[J]. Journal of Seismological Research, 2006, 29(2):176-181.

[9] 苗胜军，李长洪，文俊,等. 基于正交试验设计的滑带土参数敏感性分析[J]. 中国矿业, 2007, 9(9):76-79.

MIAO Sheng-jun, LI Chang-hong,WEN Jun ,etal. Parameter sensitivity analysis of slip zone based on orthogonal experiment[J]. China Mining Magazing, 2007, 9(9):76-79.(In Chinese)

[10]李念平，肖书博，关军.风管中聚集物燃烧时极限温度的分析研究[J].湖南大学学报:自然科学版,2009,36(6):18-21.

LI Nian-ping, XIAO Shu-bo, GUAN Jun.Analysis and study of the limit temperature of theburning sediment in ventilation ducts[J].Journal of Hunan University:Naturnal Science,2009, 36(6):18-21.(In Chinese)

[11]邓红卫，胡普仑，周科平,等. 采场结构参数敏感性正交数值模拟试验研究[J]. 中南大学学报:自然科学版, 2013, 44(6): 2463-2469.

DENG Hong-wei, HU Pu-lun, ZHOU Ke-ping,etal. Test of orthogonal numerical simulation on sensitivity of stope structure parameters[J]. Journal of Central South University:Science and Technology , 2013, 44(6): 2463-2469.(In Chinese)

[12]李炎隆，李守义，丁占峰,等. 基于正交试验法的邓肯-张E-B模型参数敏感性分析研究[J]. 水利学报, 2013, 7(7): 873-879.

LI Yan-long, LI Shou-yi, DING Zhan-feng,etal. The sensitivity analysis of Duncan-Chang E-B model parameters based on the orthogonal test method[J].Journal of Hydraulic Engineering, 2013, 7(7):873-879.(In Chinese)

[13]徐钊，许梦国，王平,等. 低强度相似材料参数敏感性正交试验研究[J]. 武汉科技大学学报, 2013, 6(6): 435-438.

XU Zhao, XU Meng-guo,WANG Ping，etal. Orthogonal experimental study of parameter sensitivity[J].Journal of Wuhan University of Science and Technology, 2013, 6(6): 435-438.(In Chinese)

[14]周小涵. 通风对寒区隧道抗防冻的影响及合理设防范围研究[D]. 成都：西南交通大学土木工程学院,2012:29-31.

ZHOU Xiao-han. Study on the influence of ventilation on frost resistance and reasonable range of resistance for tunnel in cold region[D]. Chengdu： School of Civil Engineering, Southwest Jiaotong Unniversity, 2012:29-31.(In Chinese)

[15]ZHOU Xiao-han, ZENG Yan-hua,FAN Lei.Temperature field analysis of a cold-region railway tunnel considering mechanical and train-induced ventilation effects[J].Applied Thermal Engineering, 2016,100:114-124.[16]张建荣，刘照球. 混凝土对流换热系数的风洞实验研究[J]. 土木工程学报, 2006, 9(9): 39-42.

ZHANG Jian-rong, LIU Zhao-qiu. A study on the convective heat transfer coefficient of concrete in wind tunnel experiment[J]. China Civil Engineering Journal ,2006, 9(9):39-42.(In Chinese)

[17]何川，谢红强. 多场耦合分析在隧道工程中的应用[M].成都: 西南交通大学出版社, 2007：184-184.

HE Chuan, XIE Hong-qiang.Coupling analysis application in tunnel engineering[M]. Chengdu:Southwest Jiaotong University Press, 2007:184-185.(In Chinese)

[18]张学富，苏新民，赖远明,等. 寒区隧道三维温度场非线性分析[J]. 土木工程学报, 2004, 2(2): 47-53.

ZHANG Xue-fu, SU Xin-min, LAI Yuan-ming,etal.Non-linear Analysis for three-dimensional temperature field in cold region tunnels[J]. China Civil Engineering Journal,2004, 2(2): 47-53.(In Chinese)

[19]李录娟. 亚洲地热图编制及地热潜力评估[D]. 长春: 吉林大学建设工程学院, 2011:32-36.

LI Lu-juan. The asian geothermal map and the evaluation on geothermal Potential[D]. Changchun:Construction Engineering College,Jilin University,2011:32-36.(In Chinese)

Sensitivity Analysis of Influencing Parameters on TunnelTemperature Field by Orthogonal Test Technique

ZHOU Xiao-han1,3，ZENG Yan-hua1†，FAN Lei2,ZHOU Xiao-jun1，RUAN Liang-hong1，WEI Ying-jie4

(1. Key Laboratory of Transportation Tunnel Engineering, Ministry of Education, Southwest Jiaotong Univ, Chengdu, Sichuan 610031,China； 2.Tunnel Section of First Civil Construction Design & Research Institute, China Railway ErYuan Engineering Group Co Ltd, Chengdu, Sichuan 610031,China;3.China Railway Major Bridge Reconnaissance & Design Institute Co Ltd, Wuhan,Hubei 430050,China;4.Chengdu Construction Engineering Group Corporation，Chengdu, Sichuan 610014, China)

Many factors affect the tunnel temperature field in cold region. An unsteady heat transfer calculation model was established based on finite difference method. Taking the Nan Shan railway tunnel in cold region as an example, the othogonal test method, which takes the average temperature of tunnel lining internal nodes, lining temperature of a certain section, and longitudinal frozen length of tunnel entrance as index, respectively, is applied to carry out sensitivity study of the influencing factors on tunnel temperature field. The results show that there are some local differences in the ranging of sensitivity of each factor under different indexs. Overall, the tunnel depth, wind direction in tunnel, tunnel section size, wind speed in tunnel, wind temperature of entrance, and thermal conductivity coefficient of surrounding rock are the main factors affecting the tunnel temperature field, while the surrounding rock density and specific heat of surrounding rock are the secondary factors affecting tunnel temperature field. In the antifreezing design of the tunnel in cold region, except the unchanged factors such as the surrounding rock density, surrounding rock specific heat, surrounding rock heat transfer coefficient, thermal conductivity of surrounding rock, and wind temperature of tunnel entrance, sufficient attention should be paid on the design parameters that affect significantly the tunnel temperature field including the tunnel depth, wind direction in tunnel, wind speed in tunnel, and tunnel section size.

railway tunnel in cold region；temperature field；orthogonal test；sensitivity analysis

1674-2974(2016)11-0154-07

2015-09-24

国家自然科学基金资助项目(51278426), National Natural Science Foundation of China(51278426)

周小涵(1988-)，男，重庆忠县人，西南交通大学博士研究生†通讯联系人，E-mail:zengyhua@163.com

TU91