大跨度球面网壳结构风力荷载间歇特性研究

王 旭，张俊波，黄 鹏

(1. 重庆交通大学 山区桥梁与隧道工程 国家重点实验室培育基地，重庆 400074;2.同济大学 土木工程防灾国家重点实验室，上海 200092)



大跨度球面网壳结构风力荷载间歇特性研究

王 旭1,2，张俊波1，黄 鹏2†

(1. 重庆交通大学 山区桥梁与隧道工程 国家重点实验室培育基地，重庆 400074;2.同济大学 土木工程防灾国家重点实验室，上海 200092)

针对典型大跨度球面网壳结构，在同济大学TJ-3大气边界层风洞试验室进行了刚性模型测压试验.首先，利用游程分析方法验证了风力信号的非平稳特性.其次，使用离散小波变换对其1∶200的模型结构风力信号在各尺度进行分解，得到各尺度小波系数时程曲线.为量化分析风力间歇特性，对尺度能量分布，间歇因子及间歇能量分布进行了分析和比较.研究表明：风场类型对阻力系数及Z向升力系数的平稳特性，以及对高尺度区间歇能量比率及间歇因子影响较大，而对各尺度风力系数尺度能量比率的影响均较小.各尺度下，整体阻力系数与Y向升力系数呈现正相关，而与Z向升力系数呈现负相关，并且整体阻力系数与Y向升力系数的相关性随着尺度增大而增大.

球面网壳；小波变换；风力系数；尺度能量比率；间歇因子；间歇能量比率

大跨度球面网壳结构的特点是跨度大、高度高、且覆盖面积广，由于其屋盖围护结构通常采用轻型金属材料或膜结构材料，所以使得其对风荷载的作用极为敏感，因此在结构设计中风荷载往往成为控制荷载[1].真实条件下的风荷载往往具有较强的非平稳及非高斯特征，导致结构表面会随机产生幅值较大的脉冲荷载.分析表明，结构表面非高斯风压的负压脉冲以及非平稳风压时程的瞬态间歇脉冲是导致结构风致破坏的两大主要原因[2]，但目前相关研究还存在明显不足.主要表现在脉冲风荷载具有较强的非平稳特性，而传统分析方法是孤立的对风荷载信号进行时域或频域分析，从而无法体现非平稳信号能量的时频联合分布特性.为此，文献[3]针对大跨网壳结构表面风压信号的脉冲间歇特性进行了分析，获得了风压的时频分布规律，但却尚未对可能导致结构破坏的风力荷载的间歇脉冲进行进一步的研究.目前，此类研究还相对匮乏，造成人们对风荷载间歇脉冲的作用机理的认识存在严重不足，需要进一步开展相关工作弥补现有研究的不足，从根本上提高大跨网壳结构的抗风性能.

与传统平稳随机信号的分析方法不同，小波分析方法适用于非平稳信号的分析，可以反映出信号中各频率成分能量随时间的变化.目前，该方法在故障检测、航空航天、图像识别等领域已得到广泛应用[4-6].随着结构风工程研究的逐步精细化，小波分析方法将成为该领域必不可少的一种有效的分析手段.本文以典型大跨度球面网壳结构为背景，使用离散小波变换对其1∶200的模型结构风力荷载在各尺度进行分解，验证了间歇参数的稳定性.其次，通过离散变换对尺度能量分布、间歇因子及间歇能量分布进行了分析和比较.最后，对风力系数经小波分解后在不同尺度的小波系数信号进行了相关性分析，得到不同尺度之间各向风力系数的相关性规律.

1 理论分析及数据处理

1.1 非平稳性检验

信号的非平稳性检验方法主要包括趋势分析和游程分析方法两种[7].其中，游程分析更适用于随机脉动信号的分析[8]，具体分析过程如下．

1) 先进行采样得到一系列数据样本.

3)把连续出现的“+”或“-”称为一个游程.记N1为“+”号出现的次数，N2为“-”号出现的次数，N=N1+N2,U为游程的总数.

4)检验假设H0:样本为平稳随机序列.理论上可证明U近似服从正态分布N(μ,σ2),其中

(1)

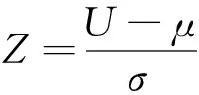
1.2 小波变换

如果函数ψ(t)∈L2(L2表示Hilbert空间)，且函数ψ(t)的傅里叶变换满足下述允许条件[9]：

(2)

那么，一维连续小波变换(CWT)将被定义为：

(3)

式中:ψ*表示小波函数ψ的傅里叶变换，a和τ表示尺度和平移参数，f(t)表示原始信号.

和傅里叶变换一样，连续变换不能进行信号的重构，因此工程中均使用基于Mallat算法[10]的离散小波变换对信号进行分析，具体定义如下：

(4)

式中m,n∈Z.

整个分解过程如图1所示，图中A表示低频带概貌信号，D表示高频带细节信号.分解过程的实质是将信号在低通滤波器的作用下以2n为尺度进行采样，每次分解产生新的概貌信号和细节信号，然后新的概貌信号再进行类似分解，直到分解结束.图2给出了经小波变换后小波系数在时域与频域上的分辨率示意.从图中可知，尺度大，它的时窗宽而频窗窄，频域分辨率高，而时域分辨率低，适合表示信号f(t)的高频部分；尺度小，它的时窗窄而频窗宽，频域分辨率低，而时域分辨率高，适合表示信号f(t)的低频部分.

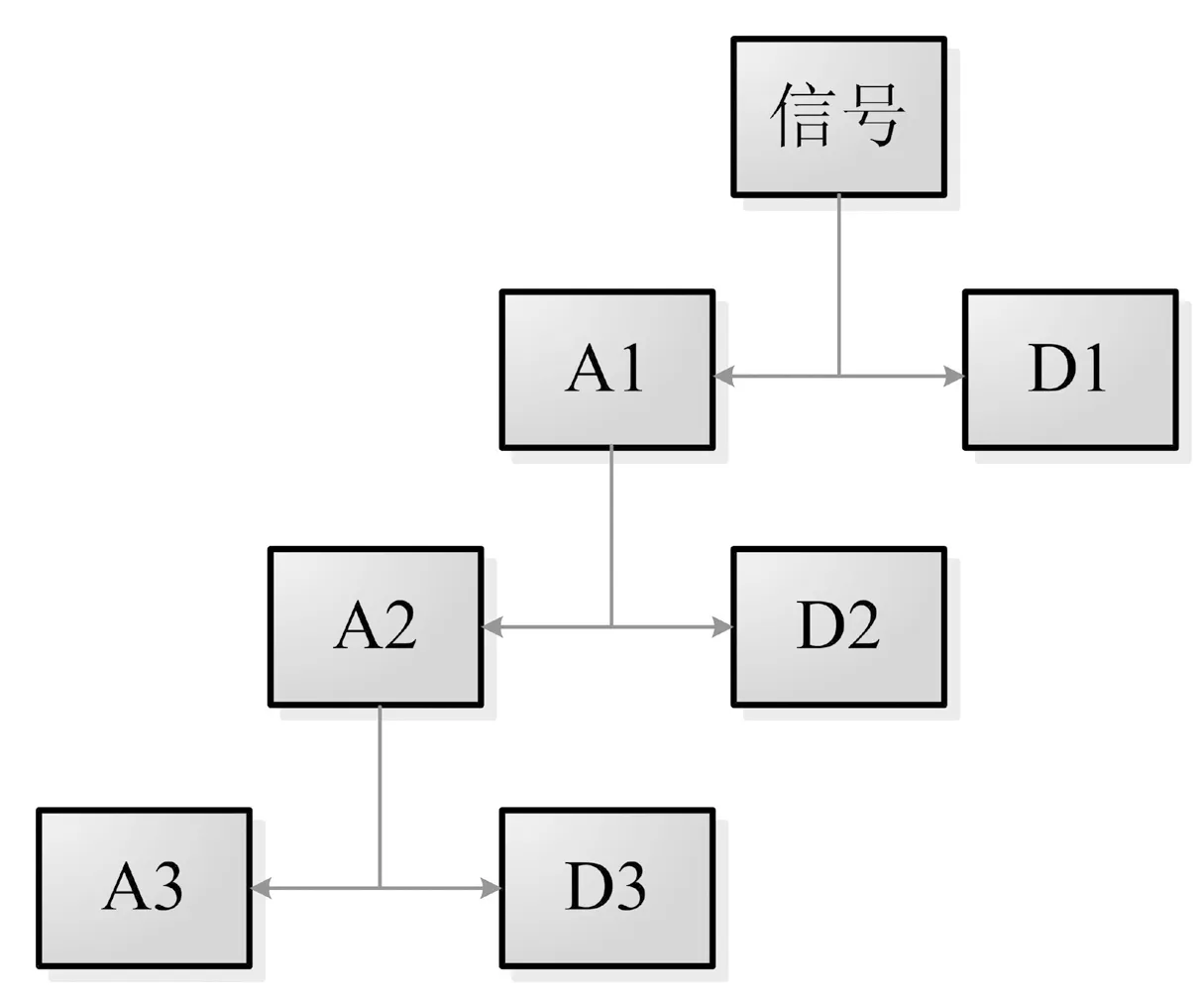
图1 小波变换过程示意图Fig.1 Schematic diagram of wavelet transform

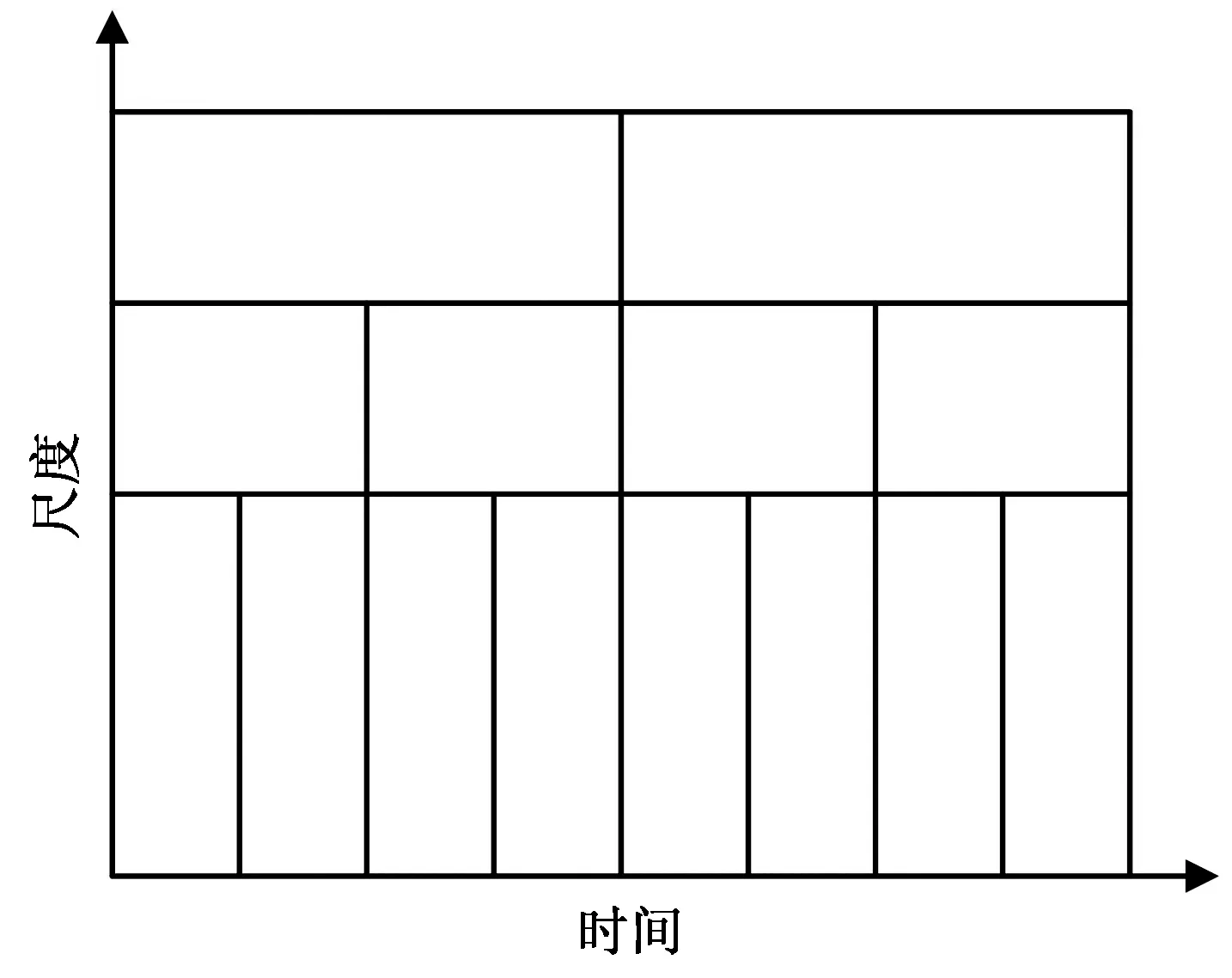
图2 时域与频域分辨率Fig.2 Resolution of time domain and frequency domain

1.3 风力系数

风力系数可以通过模型整体外表面压力积分获得，表示为：

(5)

(6)

(7)

式中：CD，CL(Z)和CL(Y)分别表示阻力系数、Z向升力系数和Y向升力系数；Ai表示i测点的有效附属面积；AH和AV分别为结构物水平及竖直投影面积；θ为风向角;r为环向角.

1.4 间歇特性参数

为了定量化分析脉冲信号的非平稳间歇特性，本文定义了表征间歇特性的3类参数[11].

1)尺度能量比率SE：表征特定尺度能量在总能量中的比重.公式如下：

(8)

式中:ES表示特定尺度能量，E表示总能量.

2)间歇能量比率IE：表征能量超过某一阈值的特定尺度能量之和与该尺度总能量的比值(本文中阈值取此尺度平均能量的两倍).公式如下：

(9)

式中:Ethreld表示超过某一阈值的特定尺度能量之和，ES表示特定尺度能量.

2)间歇因子IF：表征能量超过某一阈值的小波系数的个数与该尺度总的小波系数的比值(本文中阈值取此尺度平均能量的两倍).公式如下：

(10)

式中:Nthreld表示能量超过某一阈值的小波系数的个数，N表示特定尺度小波系数个数.

2 风洞试验概况

在同济大学土木工程防灾国家重点实验室风洞试验室的TJ-3大气边界层风洞中进行了刚性模型同步测压试验，试验在模拟的A类及B类风场中进行，采样频率312.5样Hz，采样时间19.2 s，采样次数4次.图3给出了风洞中模拟的A类地貌平均风速、紊流度剖面以及风速谱，图中风速剖面指数为0.12，试验模型顶部的紊流度为10%.

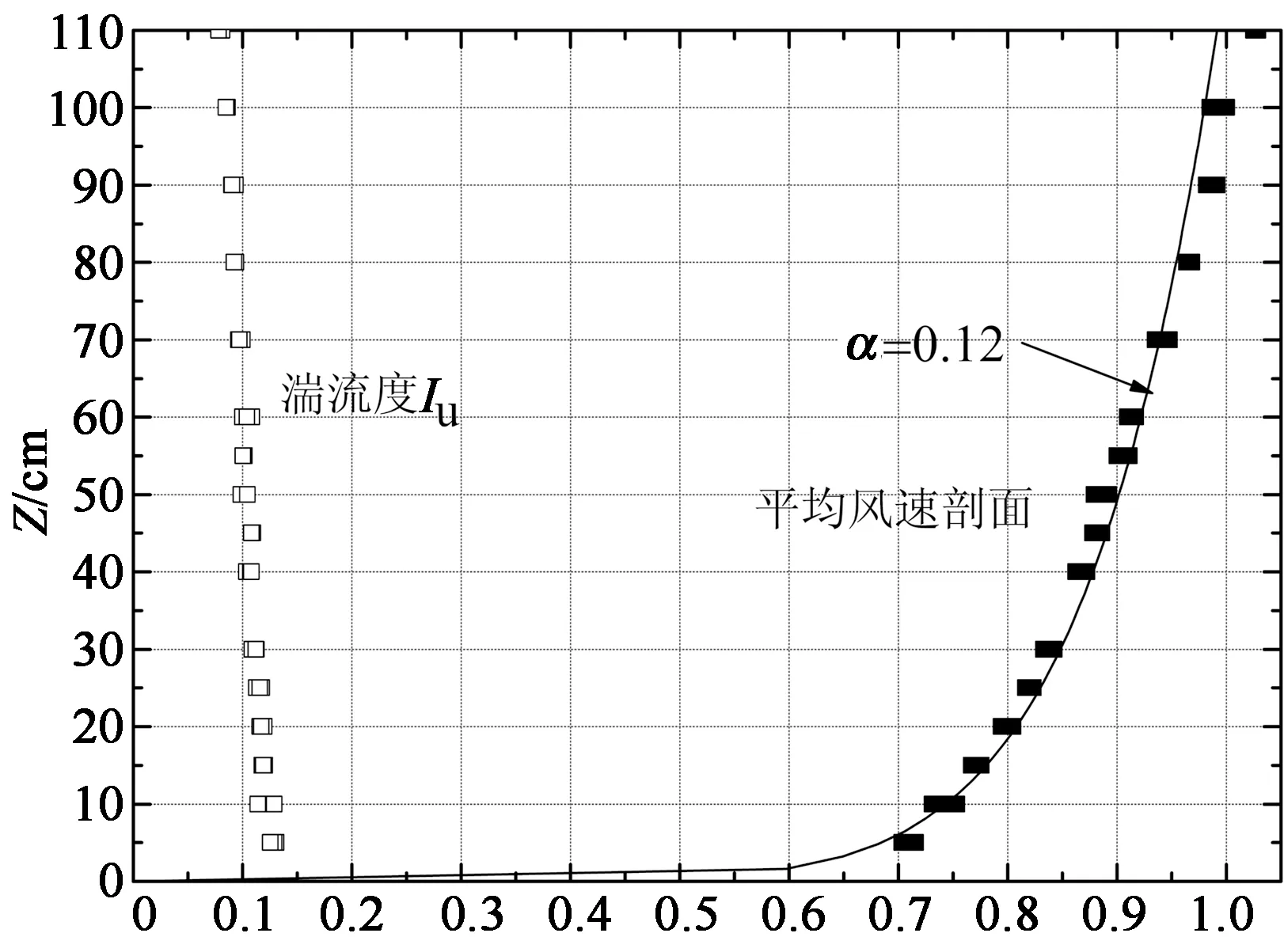
U/US(a)风洞中模拟的A类地貌平均风速和紊流度剖面

nz/U(b) 风洞中模拟的脉动风功率谱 (a：Davenport谱；b：Kaimal谱；c：Karman谱)图3 A类风场风剖面和功率谱Fig.3 Mean wind speed profile and power spectrum for A terrain

该大跨球面空间网壳结构，跨度132 m，高69 m.模型的几何缩尺比选为1/200，模型与实物在外形上保持几何相似，模型实物图如图4所示.

图4 试验模型Fig.4 Test model

如图5所示，在模型结构表面共布置了169个测点.其中1～6 层各布置24个测点，7层布置12个测点，8层布置8个测点，9 层布置5个测点.

(a)

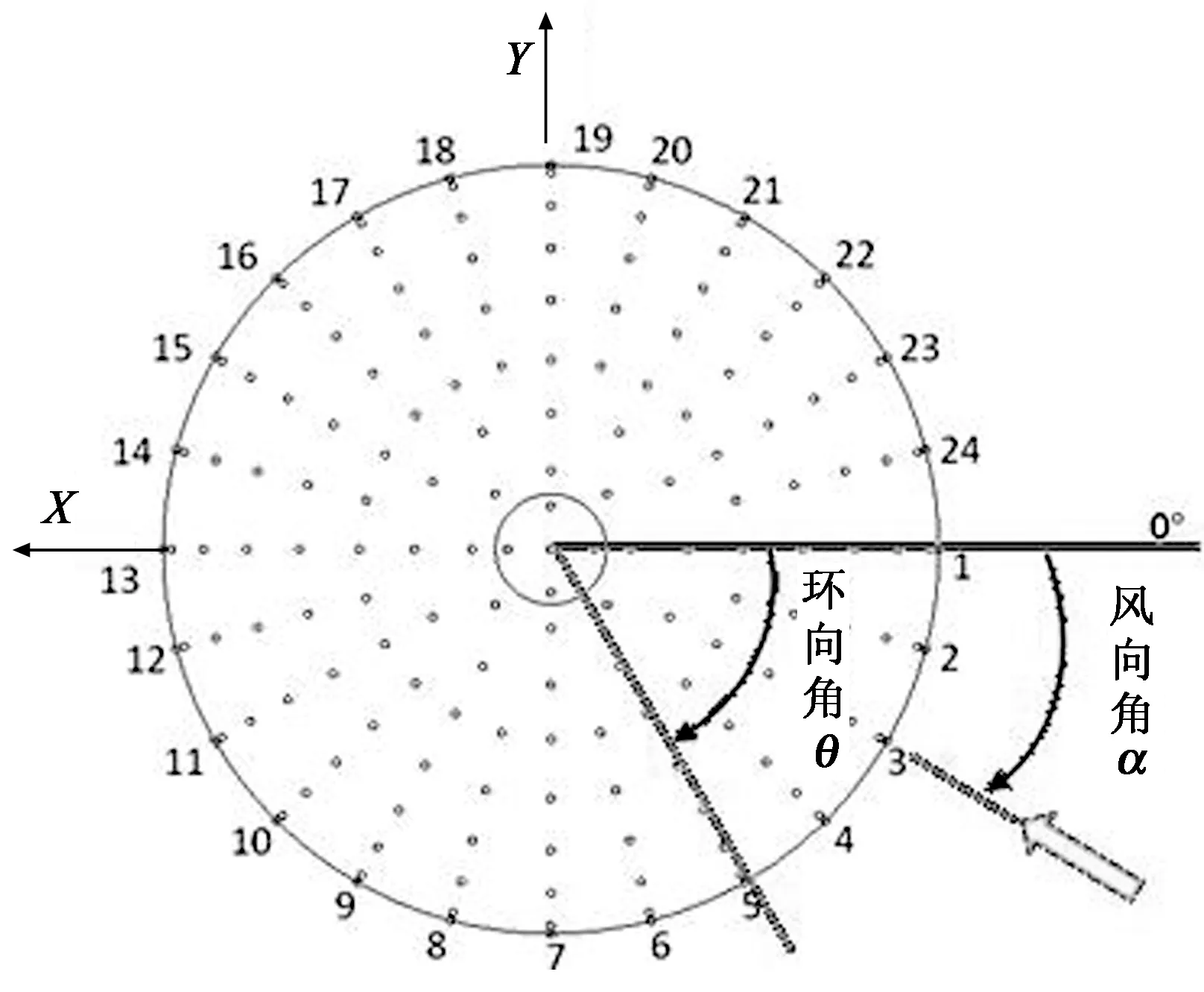
(b)图5 模型测点布置及角度参数定义Fig.5 The arrangement of model test points and the definition of angle parameters

3 试验结果及分析

3.1 风力系数平稳性检验

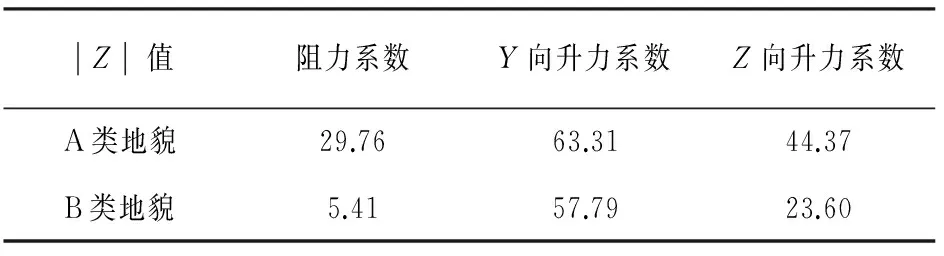
表1 风力系数平稳性检验Tab.1 Stationarity test of wind force coefficients

3.2 间歇特性分析

由于小波变换具有在高频时间分辨率高，低频时间分辨率低的特点，与湍流特性相符，因此非常适合用于分析湍流的能值和间歇特性.由于数据长度为6 000，所以最大分解层数为12层[12-13]，随着尺度从1～12，信号频率逐渐降低.表2给出了尺度m与其代表的频域范围之间的对应关系，可以看出随着尺度的增加，频率范围逐渐减为上一尺度的一半.全尺度对应的频率范围为0.04～156.25 Hz，均在研究范围之内，因此后文选取了尺度1～12进行分析.

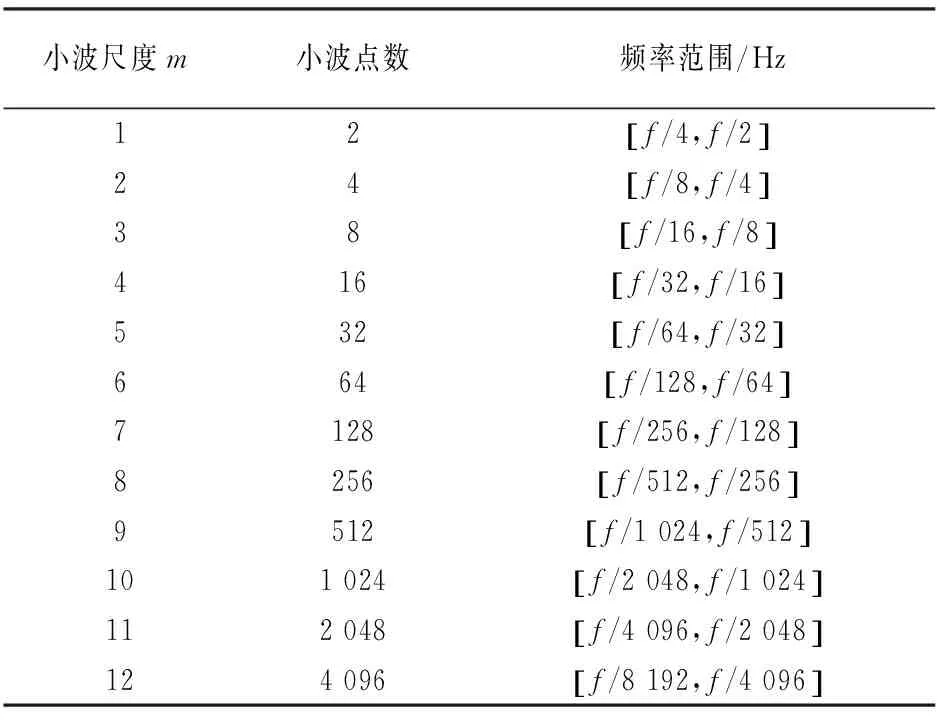
表2 小波尺度与频域范围对应关系Tab.2 The relationship between wavelet scalogram and frequency

注：f表示采样频率，本文中f=312.5 Hz.

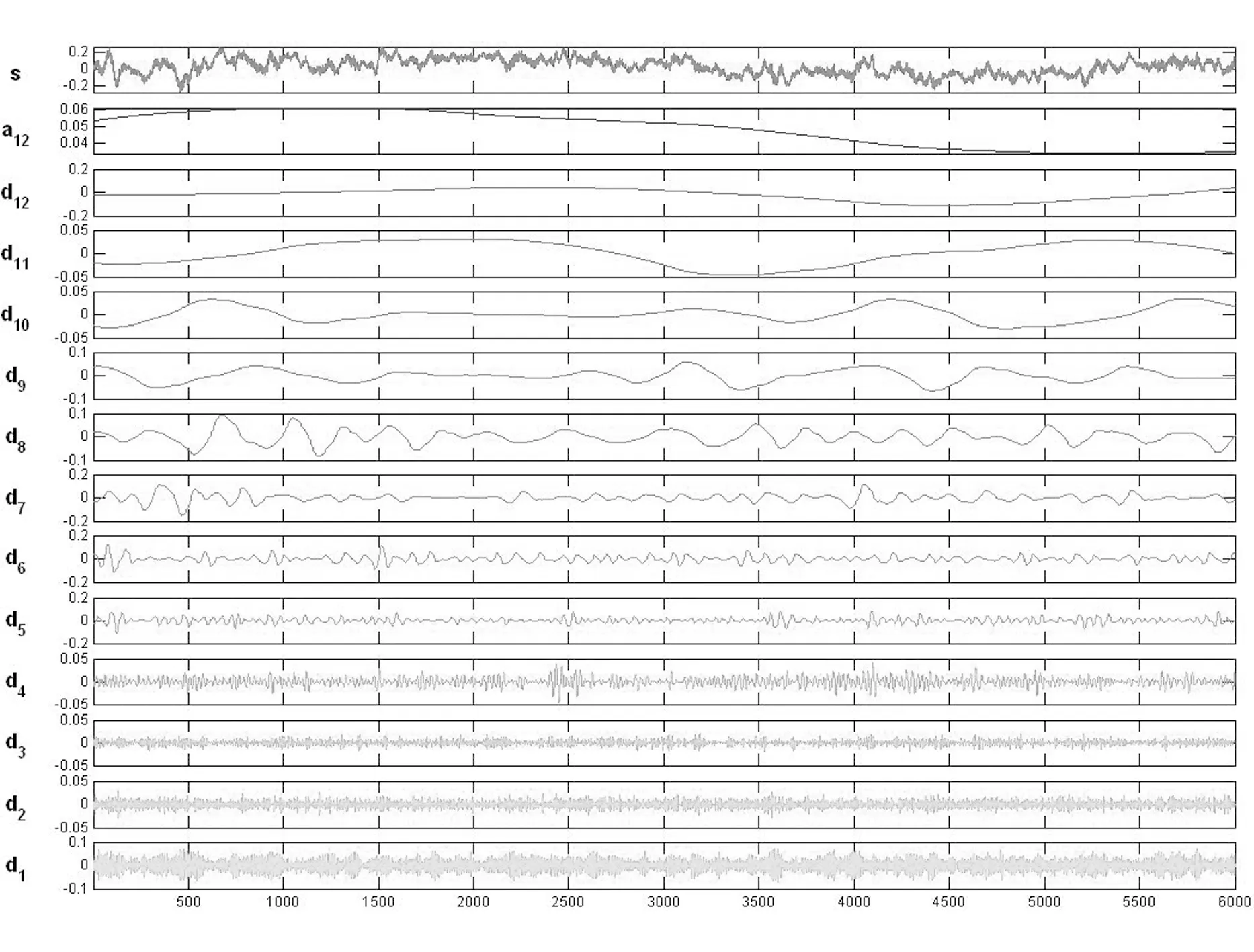
由于采样的随机性强，一次采样结果可能不能反映其本质特性，因此本文对风力时程进行了4次重复采样.图6给出了其中一次采样信号经离散小波分解得到的概貌信号和细节信号示意图.从图中可以看到原始信号的时程曲线及信号中各尺度小波系数随时间的变化曲线，其中a表示概貌分量，d表示细节分量，后面数字表示尺度m.可以看到当信号在某时刻出现明显波动时，在某些特定尺度的相同时段也会表现出大的系数波动.说明信号的间歇特性是由特定尺度的信号波动引起的.

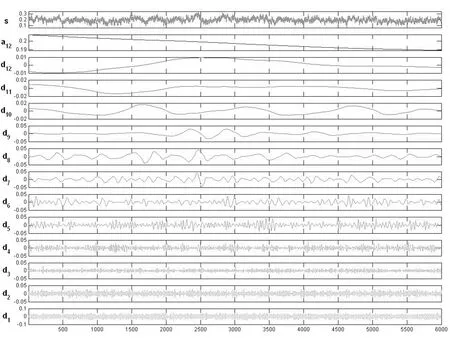
(a)A类风场阻力系数

(b) B类风场阻力系数

(c) A类风场Y向升力系数

(d) B类风场Y向升力系数

(e) A类风场Z向升力系数

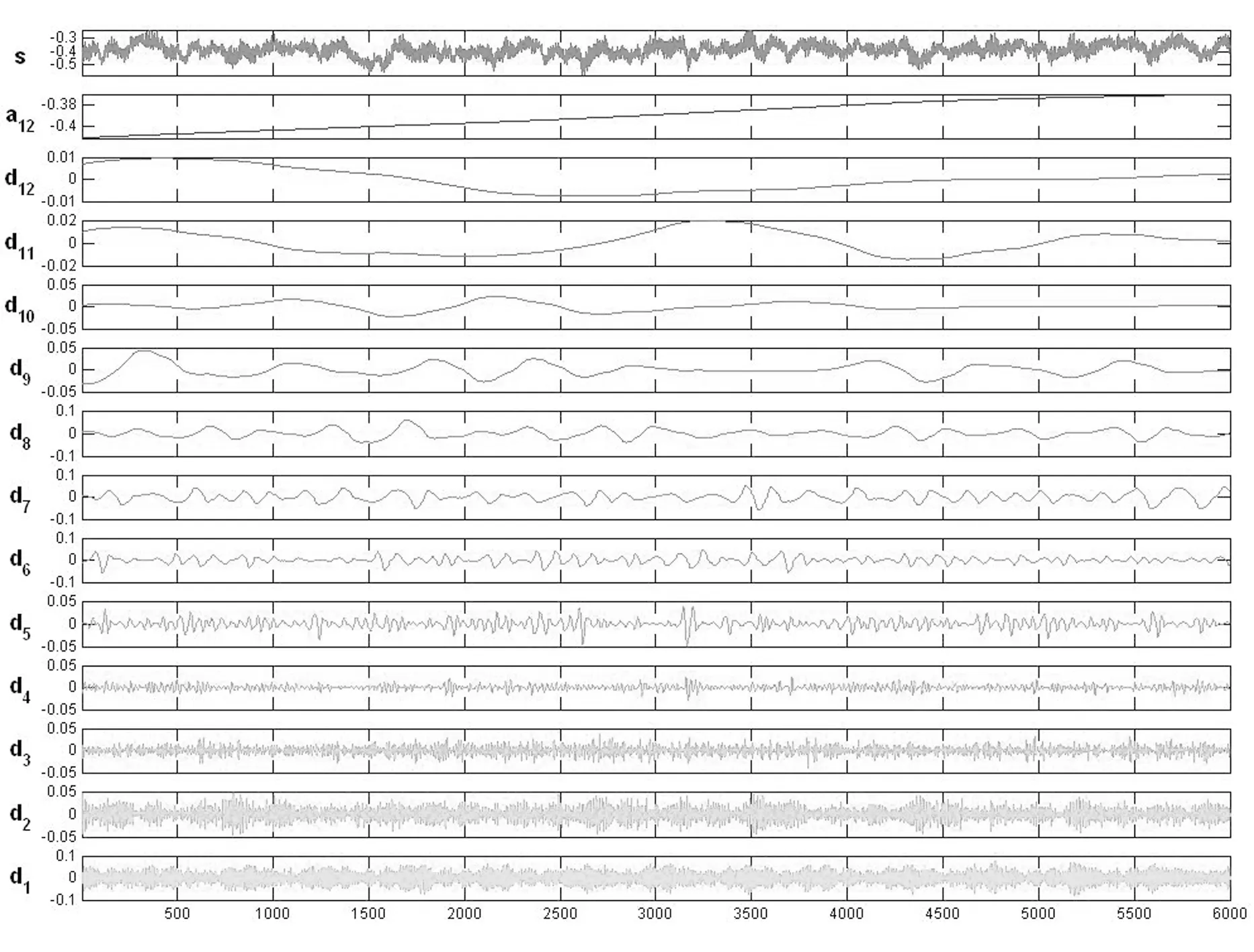
(f) B类风场Z向升力系数图6 离散小波变换Fig.6 Discrete wavelet transform

为了验证风力信号间歇变化的稳定性，对4次采样时程分别进行了间歇特性分析并进行比较，由于篇幅有限只针对整体阻力系数进行分析，如图7所示.从图中可以看出，不同采样得到的间歇参数随尺度变化趋势基本一致，数值略有差距，且均集中于高尺度区域.以7(b)图为例，在尺度1～10之间，4次采样结果极为相近，但在尺度11和12处，最大差值分别为0.3和0.4，占4次采样均值的15%和19%.(a)和(c)图与(b)图结论相似.综合以上分析可以得出，风力信号间歇变化总体上具有较好的稳定性，只是在个别高尺度处差值较大.为此，后文中间歇参数均采用4次采样结果的均值表示.

图6虽然将风力系数的时域信号在各尺度进行了分解，但对于研究间歇变化还是不够直观.为了进一步量化分析，图8～图10分别给出了两类风场下整体阻力系数，Y向整体升力系数及Z向整体升力系数时程的间歇特性参数随尺度变化的曲线.从图8可以看出，无论是整体阻力系数还是两个方向的整体升力系数，风场类型对尺度能量比率的影响均较小.3种风力系数尺度能量比率随尺度的变化趋势基本一致，在尺度1～11之间，尺度能量随尺度增大而缓慢增大，而在尺度12出现明显激增.可以看出尺度12的能量占总能量的比重最大，而且远大于其他尺度.以Y向整体升力系数为例，在尺度12处尺度能量比率达到90%，说明此信号低频带含量占绝对优势，而其它频带含量极少.

Scale (a)间歇能量比率

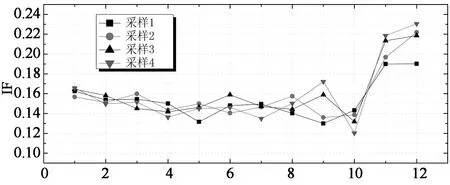
Scale (b) 间歇因子

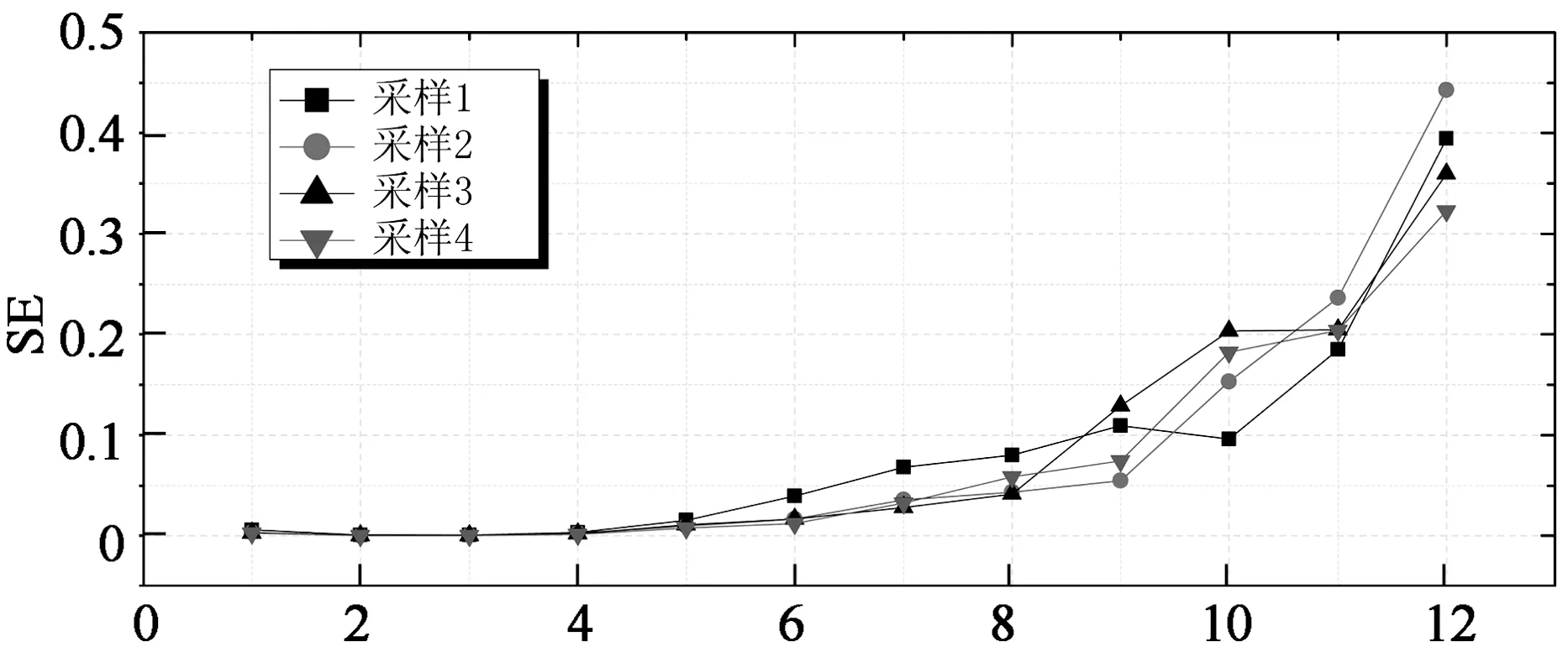
Scale (c) 尺度能量比率图7 间歇变化稳定性分析Fig.7 Stability analysis of intermittent characteristics

图9给出了间歇能量比率随尺度的变化曲线，可以看出风场类型对高尺度区间歇能量比率的影响较大.尺度12处，9(a)中A类风场下得到的结果明显大于B类风场下的结果，两者差值约为0.17，而在9(b)和9(c)中得到了相反的结论；尺度11处，9(a)中A类风场下得到的结果略小于B类风场下的结果，差值约为0.07，而9(b)和9(c)中B类风场下的结果却远小于A类，分别只为A类结果的0.5和0.6；尺度10处，(a),(b),(c)得到的结论一致，A类风场下的结果均明显小于B类.综上分析可以看出图(b)和(c)曲线随风场类型的变化基本一致，而与整体阻力系数略有不同.

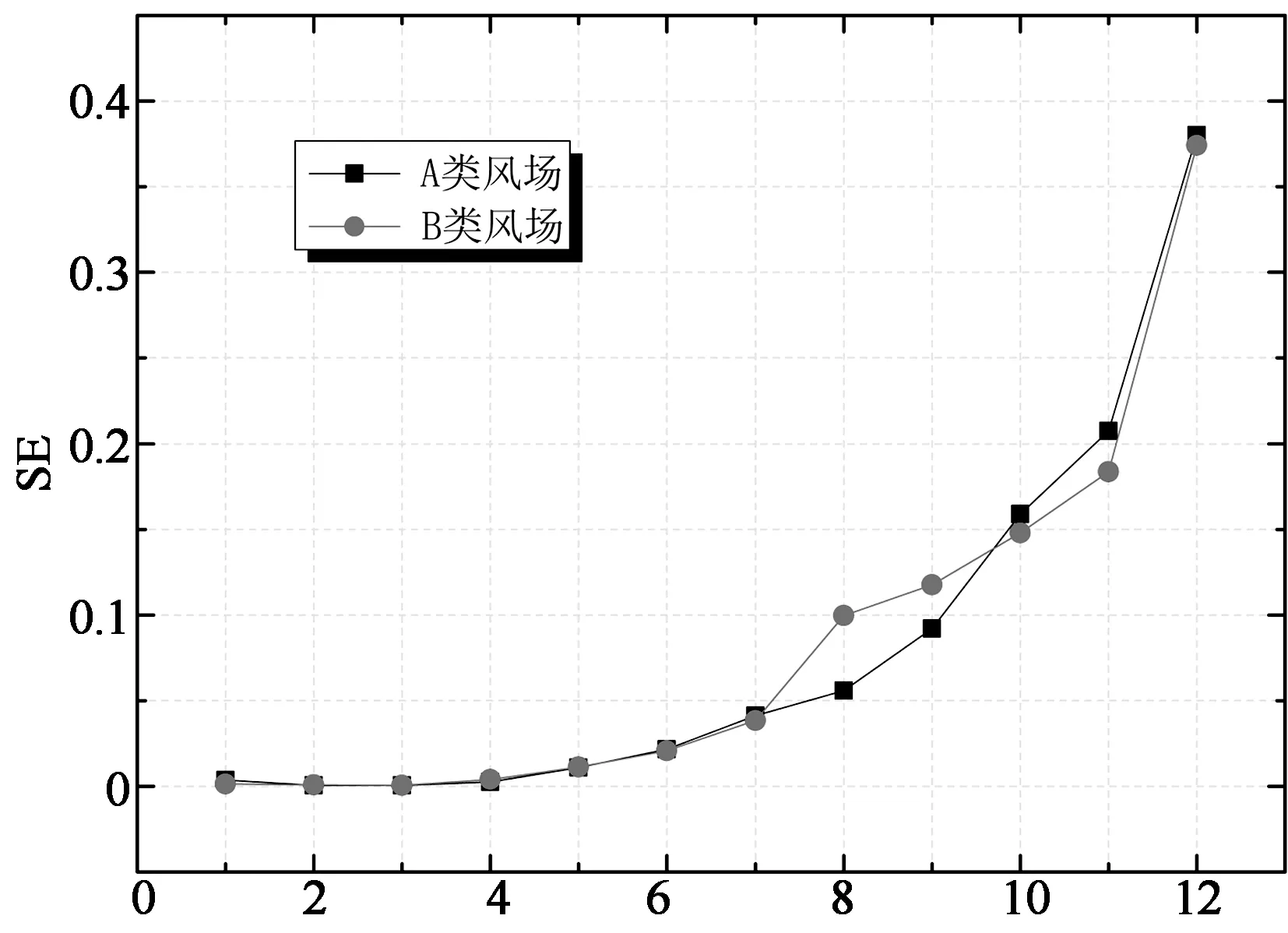
Scale (a) 整体阻力系数

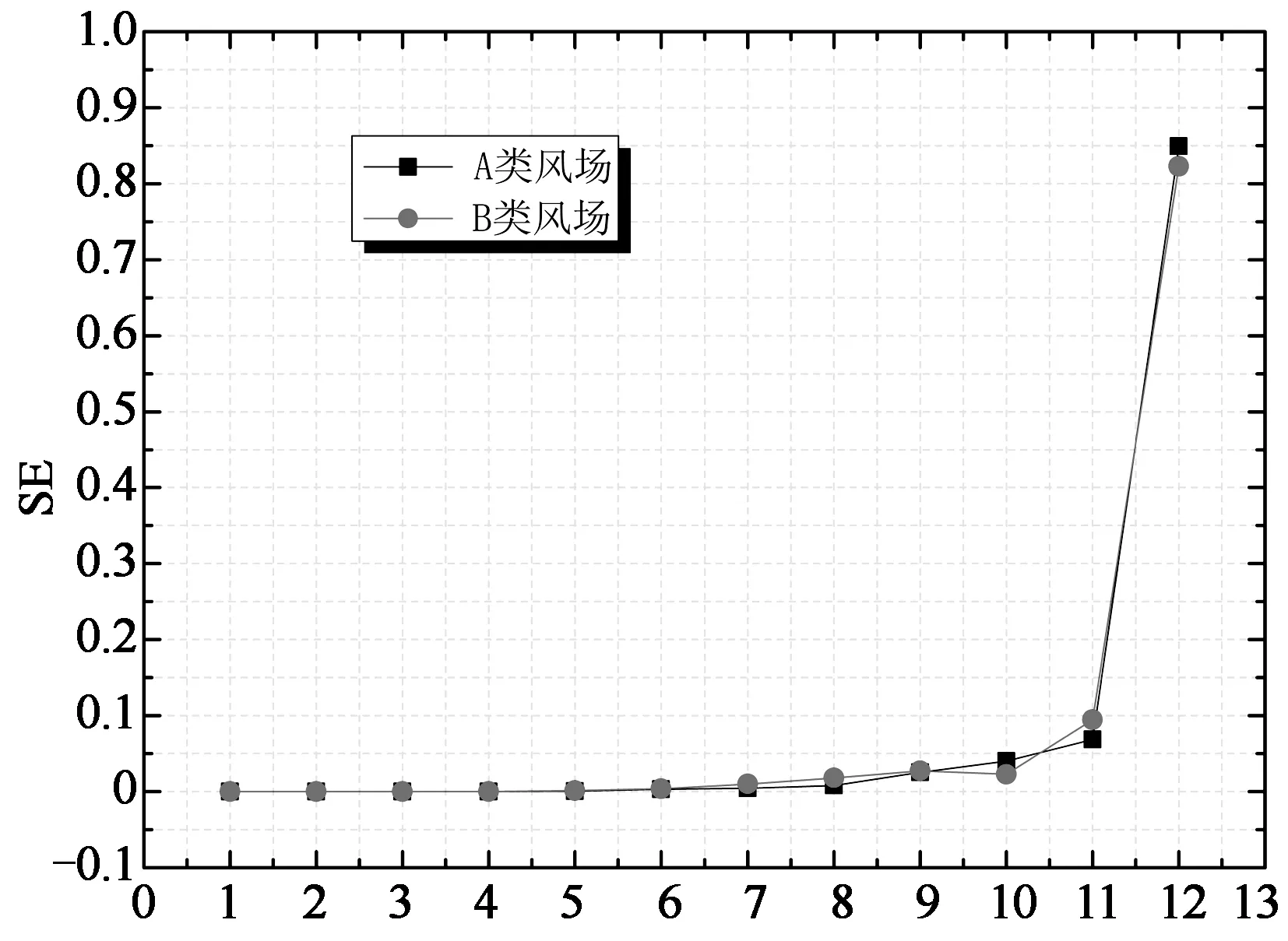
Scale (b) 整体Y向升力系数

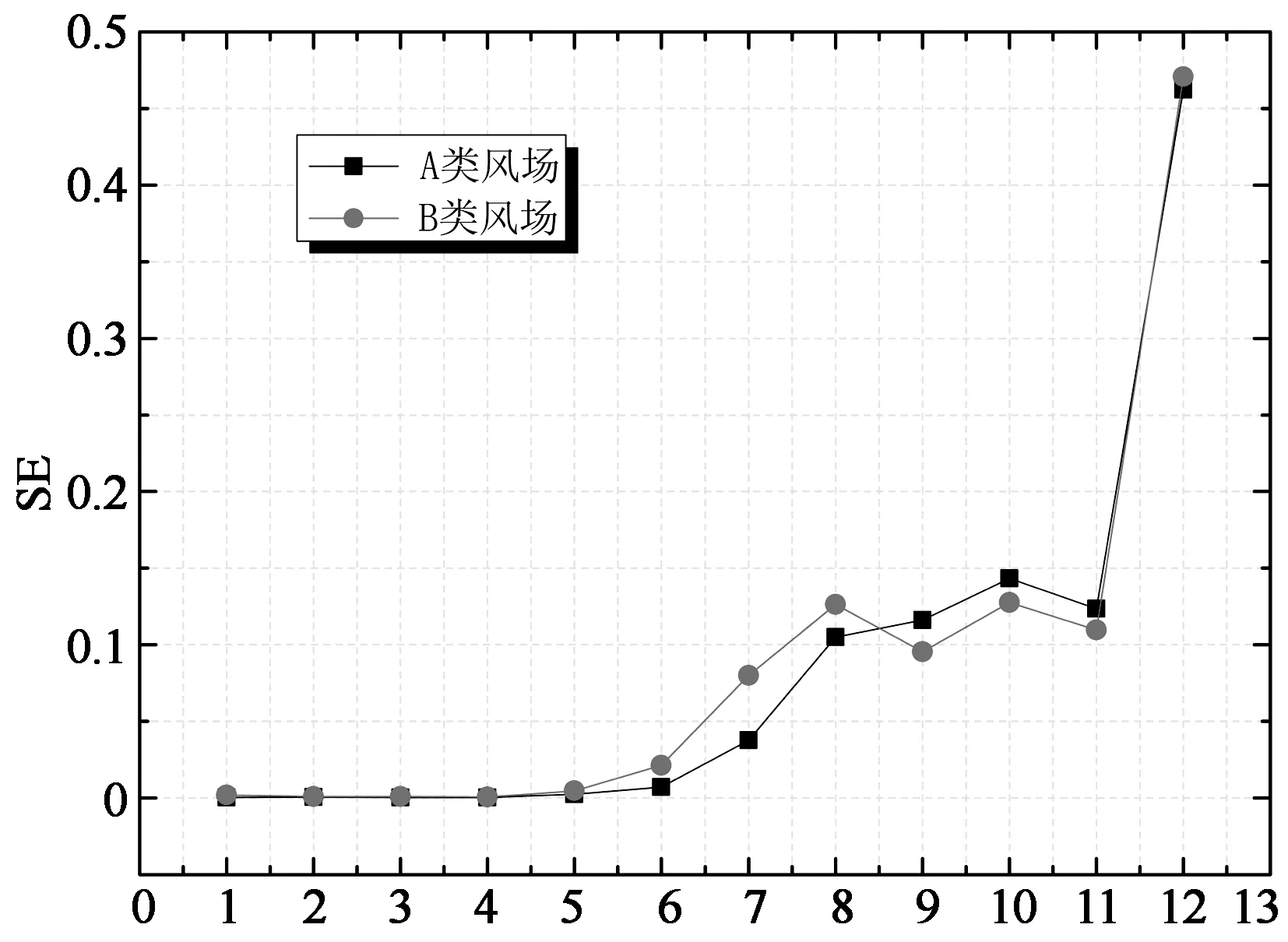
Scale (c) 整体Z向升力系数图8 尺度能量比率随尺度的变化曲线Fig.8 The variation of scale energies with scales

图10给出了间歇因子随尺度的变化规律.图中可见风场类型对高尺度区的结果影响较大.首先从10(a)可以看出，尺度1～4之间，风场影响较小；尺度5～7之间，A类风场得到的结果大于B类，而尺度8～11结论相反；在尺度12处，A类风场得到的结果突然增大，达到0.26，而B类风场得到的结果较尺度11略有增大，只为0.21.其次可以看出，在高尺度区，10(b)和10(c)图的变化规律与图9中相应曲线的变化趋势相似，说明两者具有一定的相关性.

Scale (a) 整体阻力系数

Scale (b) 整体Y向升力系数

Scale (c) 整体Z向升力系数图9 间歇能量比率随尺度的变化曲线Fig.9 The variation of intermittent energies with scales

3.3 尺度相关特性分析

相关性分析是考察两个变量之间线性关系的一种统计分析方法.传统的分析方法[14]是直接对某时域信号与另一信号形成的互相关系数进行分析，进而可以直观的判断两种信号之间的内在相关程度，但却不能了解非平稳信号各种频段信号之间的相关特性.为了弥补这一不足，本文采用经小波分解后不同尺度的小波系数信号进行相关性分析[15].图11给出了两类风场下，3种风力系数之间尺度相关系数变化曲线.从11(a)图可知，两类风场下，整体阻力系数与Y向升力系数呈现正相关，且随着尺度的增大相关性不断增大.例如A类风场下，在尺度1～10之间，相关系数在-0.1～0.4之间缓慢增大，在尺度11处出现激增，达到0.8，最终在尺度12处增大到0.92.与图11(a)不同，图11(b)和11(c)均呈现出一定的负相关特性.以(c)为例，Y向升力系数与Z向升力系数的相关性在尺度1处接近为0，随着尺度的增大相关性不断向负值方向增大.

Scale (a) 整体阻力系数

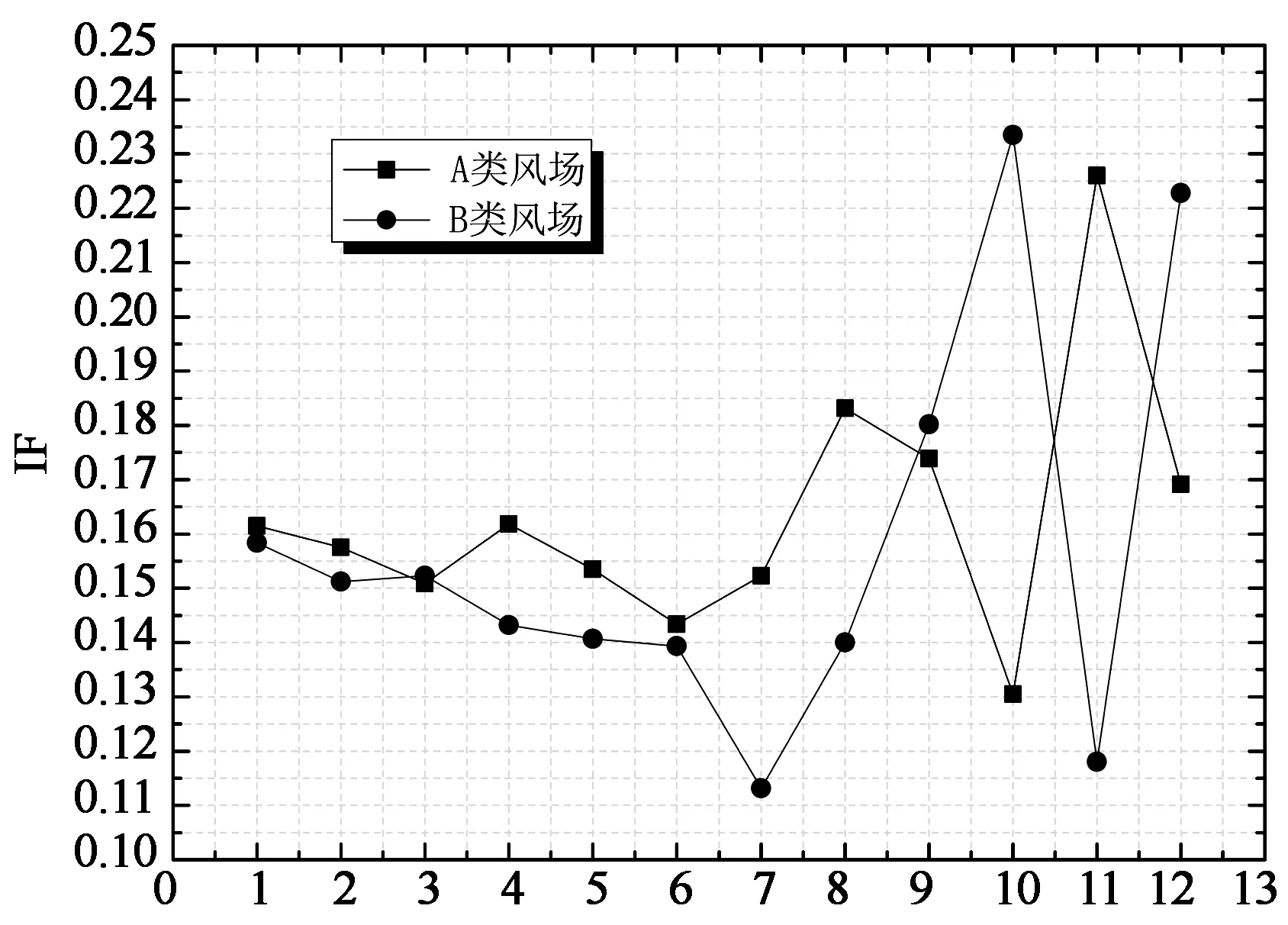
Scale (b) 整体Y向升力系数

Scale (c) 整体Z向升力系数图10 间歇因子随尺度的变化曲线Fig.10 The variation of intermittent factors with scales

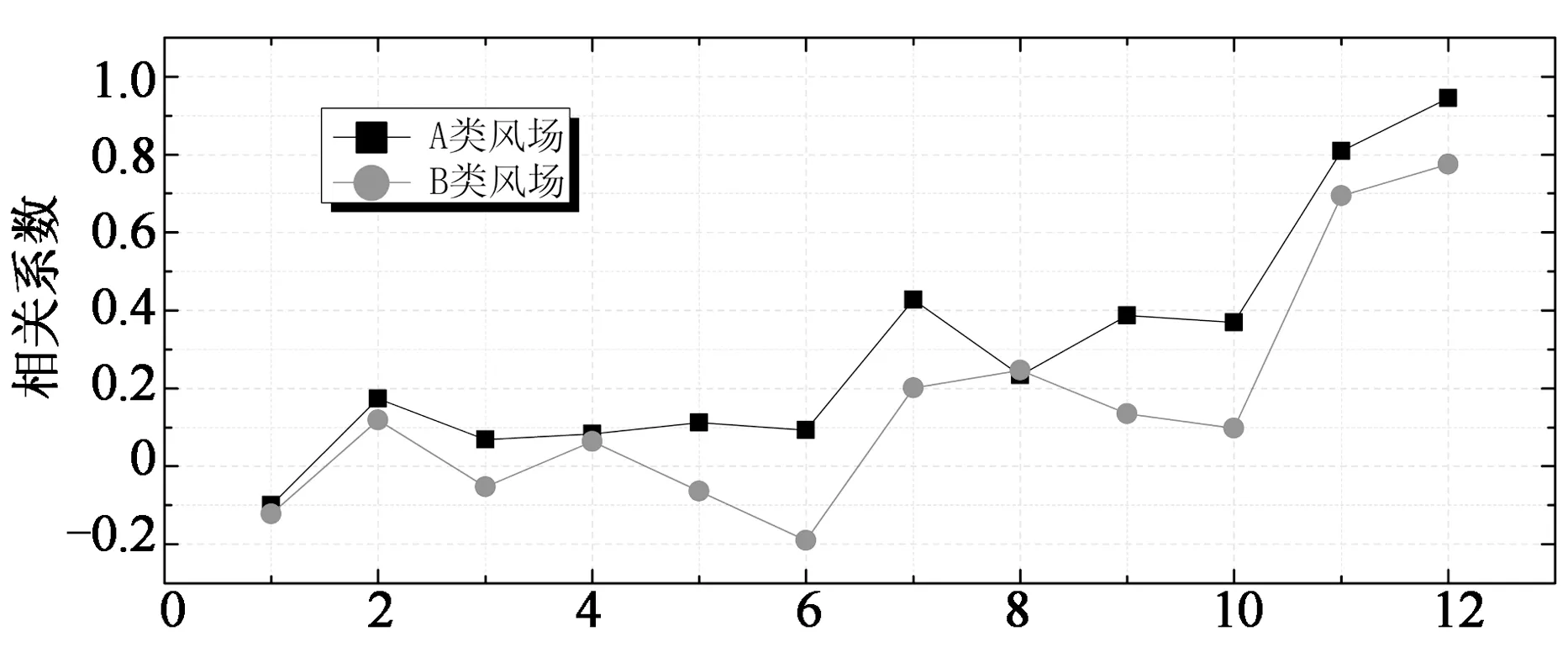
Scale (a)整体阻力系数与Y向升力系数的相关性

Scale (b)整体阻力系数与Z向升力系数的相关性

Scale (c)Y向升力系数与Z向升力系数的相关性图11 尺度相关性分析Fig.11 The correlation analysis of scales

4 结 论

本文以典型大跨度球面网壳结构为背景，利用离散小波变换对结构整体风力间歇特性进行了分析，得到以下结论：

1)整体风力信号均为非平稳随机过程.风场类型对阻力系数及Z向升力系数的平稳特性影响较大，而对Y向升力系数影响较小.

2)风力信号间歇变化总体上具有较高的稳定性，只是在个别高尺度处差值较大.风场类型对各尺度风力系数尺度能量比率的影响均较小，而对高尺度区间歇能量比率及间歇因子的影响较大.

3)各尺度下，整体阻力系数与Y向升力系数呈现正相关，而与Z向升力系数呈现负相关.整体阻力系数与Y向升力系数的相关性随着尺度增大而增大；Y向升力系数与Z向升力系数的相关性随着尺度增大而向负值增大.

[1] 李元齐, 田村幸雄, 沈祖炎. 球面壳体表面风压分布特性风洞试验研究[J]. 建筑结构学报, 2005, 26(5): 104-111.

LI Yuan-qi , TAMURA Y , SHEN Zu-yan. Wind tunnel tests for wind pressure distribution on spherical shells[J]. Journal of Building Structures, 2005, 26(5): 104-111.(In Chinese)

[2] JANAJREH I M. Wavelet analysis of extreme wind load on low-rise structures[D].Blacksburg: Virginia Polytechnic Institute and State University, 1998.

[3] 王旭, 黄鹏, 顾明. 大跨度球面网壳结构表面风压间歇特性研究[J]. 噪声与振动控制,2011,32(6):15-19.

WANG Xu, HUANG Peng, GU Ming. Experimental study on intermittent characteristics of wind pressure on long-span spherical shell's surface[J]. Noise and Vibration Control,2011,32(6):15-19.(In Chinese)

[4] MOULIN P, LIU L. Analysis of multi-resolution image denoising schemes using generalized gaussian and complexity priors[J]. IEEE Trans Information Theory, 1999, 45(3):909-919.

[5] OVANESOVA A V, SUAREZ L E. Applications of wavelet transforms to damage detection in frame structures[J]. Engineering Structures,2004,26:39-49.

[6] CHANG S G, YU B, VETTERLI M. Adaptive savelet thresholding for image denoising and compresson[J]. IEEE Trans Image Processing, 2000, 9(9):1532-1546.

[7] LEVITAN M L. Statistical analysis to validate full scale wind and structure response data[D].Lubbock:Texas Tech University, 1988:54-56.

[8] 何迎晖, 钱伟民. 随机过程简明教程[M].上海：同济大学出版社，2004:265-266.

HE Ying-hui, QIAN Wei-min. Simple tutorial on random process[M]. Shanghai: Tongji University Press, 2004: 265-266. (In Chinese)

[9] 崔锦泰.小波分析导论[M]. 西安：西安交通大学出版社,1995:13-14.

CUI Jin-tai. Introduction to wavelet analysis[M]. Xian: Xian Jiaotong University Press, 1995: 13-14.(In Chinese)

[10]MALLAT S. A Theory for multiresolution signal decomposition: the wavelet representation[J]. IEEE Pattern Analysis and Machine Intelligence, 1989,11(7): 674-693.

[11]HAJJ M R, TIELEMAN H W, TIAN L. Wind tunnel simulation of time variations of turbulence and effects on pressure on surface-mounted prisms[J]. Wind Engineering and Industrial Aerodynamics, 2000, 88: 197-212.

[12]LI Hong-jun, CHEN Xiao-chun, OUYANG Qin,etal. Wavelet analysis on fluctuating characteristics of airflow in building environments[J]. Building and Environment,2007,42: 4028-4033.

[13]刘江,王元.利用静态小波变换的非定常阵风分析与模拟[J].西安交通大学学报, 2009,43(7):74-78.

LIU Jiang, WANG Yuan. Stationary wavelet transform based analysis and simulation of unsteady gust[J]. Journal of Xian Jiaotong University, 2009,43(7):74-78. (In Chinese)

[14]李秋胜,陈伏彬,傅继阳,等.大跨屋盖结构风荷载特性的试验研究[J].湖南大学学报:自然科学版, 2009,36(8):12-17.

LI Qiu-sheng, CHEN Fu-bin, FU Ji-yang,etal. Experimental investigation of the wind load characteristics of long span roof[J]. Journal of Hunan University:Natural Sciences, 2009,36(8):12-17. (In Chinese)

[15]GEURTS C P W, HAJJ M R, TIELEMAN H W. Continuous wavelet transform of wind and wind-induced pressures on a building in suburban terrain[J]. Wind Engineering and Industrial Aerodyn Amics, 1998, 74/76 :609-617.

Experimental Study on Intermittent Characteristics of Force Coefficient of Long-span Spherical Shells

WANG Xu1，2,ZHANG Jun-bo1, HUANG Peng2†

(1. State Key Laboratory Breeding Base of Mountain Bridge and Tunnel Engineering, Chongqing Jiaotong Univ,Chongqing400074, China; 2．State Key Laboratory of Disaster Reduction in Civil Engineering, Tongji Univ, Shanghai 200092, China)

The pressure measurement of rigid model for long-span spherical shells structure was conducted at TJ-3 wind tunnel laboratory. Firstly, the non-stationary characteristics of wind pressure signals were verified by the run theory. Secondly, the wind signals of 1∶200 model structures were decomposed in the different scales by discrete wavelet transform, and the time-history curves of wavelet coefficients were obtained. For the quantitative analysis of intermittent characteristics of wind, the distribution of scale energy, intermittent factors, and intermittent energy were analyzed and compared. The studies show that wind field category had great influence on the stationary characteristics of drag coefficient andZ-direction lift coefficient as well as the intermittent energy ratio and intermittency factor in high scale region, but had small influence on the scale energy ratio of wind coefficients in the different scales. In the different scales, the overall drag coefficient presents positive correlation withY-direction lift coefficient and negative correlation withZ-direction lift coefficient. In addition, the correlations between overall drag coefficient andY-direction lift coefficient increased with the increase of scales.

spherical shells; wavelet transform; force coefficient; scale energy ratio; intermittent factor; intermittent energy ration

1674-2974(2016)11-0078-08

2015-12-07

国家自然科学基金资助项目(51378396)，National Natural Science Foundation of China(51378396); 中国博士后科学基金资助项目(2014M560706)

王 旭(1982-)，男，天津人，重庆交通大学副教授，博士†通讯联系人，E-mail:huangtju@tongji.edu.cn

TU312．1

A