单元解体法精确求解梁元无应力构形

董道福，陈常松，颜东煌，涂光亚，袁 明

(1. 长沙理工大学 桥梁工程湖南省高校重点实验室, 湖南 长沙 410114; 2. 长沙理工大学 土木与建筑学院，湖南 长沙 410114)



单元解体法精确求解梁元无应力构形

董道福1,2，陈常松2†，颜东煌2，涂光亚2，袁 明2

(1. 长沙理工大学 桥梁工程湖南省高校重点实验室, 湖南 长沙 410114; 2. 长沙理工大学 土木与建筑学院，湖南 长沙 410114)

基于非线性二阶梁柱理论及CR-UL全量求解方法，利用单元解体理论(几何法及零作用法)精确求解平面结构中梁元的完整无应力构形.利用目标构形几何信息及其对应的单元抗力直接求解梁元无应力构形基本参数；采用几何法直接进行坐标转换即得构件单元完整无应力构形；采用零作用法并利用无应力构形基本参数进行逆向计算亦可求解其完整无应力构形；编写程序对提出的两种方法进行了算法及最终结果的验证.结果表明利用几何法可在不建立结构有限元模型的条件下精确高效求解构件的完整无应力构形，利用零作用法亦可精确求解构件完整无应力构形，但需编写完善的几何非线性程序.

几何非线性；无应力构形；单元解体理论；几何法；零作用法；CR-UL全量理论

对大跨度柔性结构进行几何非线性分析[1-3]时，若能充分利用构件单元具有的某些不变量联系前后时间节点将使过程变得更富效率.无应力状态参数(例如索单元长度，梁(杆)单元曲率及长度)即具有这样的功能[4-6]，由此类参数可以构成针对构件单元不同时间节点位形进行准确描述的各类构形，并据此建立完善的基于悬链线及梁柱理论的非线性有限元计算理论.精确且快速的求解构件单元的无应力构形具有重要意义.

可将实际工程中涉及到的几种描述构件单元不同时间节点所处的位形分别定义：1)目标构形(Objective Configuration)——预先指定的结构构件达到某种随时间节点定义的状态线形；2)无应力构形[7](Unstressed Configuration)——试将结构(构件)单元解体，卸除其中所有的内力后得到的各单元密贴联接状态下的构形.工厂预制完成的制造构形(Manufacturing Configuration)亦是其中一种；3)安装构形(Construction Configuration)——试将构件单元按无应力构形确定的相对关系于施工现场进行栓焊组联，随后承受实际对应的外荷载，该构形中的一部分单元将成为有应力状态，其他未组拼部分则仍为无应力状态，这种混合式的状态称为安装构形.上述3种构形具有如下内涵：目标构形强调与既定状态的重合性；无应力构形强调构件单元的无应力参数及单元之间的相对(夹角)关系；安装构形则有效的联系无应力构形与目标构形，其起始时刻即是一种无应力构形，最终时刻则对应目标构形.利用无应力构形可建立适用于结构施工全过程非线性分析的完整计算理论.

结构整体计算中涉及到的柔性索元无应力长度的精确求解已在文献[8]中得到理想的解答.现阶段求解梁元无应力构形的方法[9]主要有：1)单元解体法[10]——按照“放松→组装→制造”过程求解梁单元无应力构形的基本思路是在单元级别由力反算变形；2)切线拼装迭代法——以目标构形作为初始安装构形，按切线拼装法逐阶段计算，得到恒载挠度曲线，将其反号后叠加上述目标构形作为下一轮计算的初始安装构形并循环此过程，直至最后得到的构形为预期目标构形；3)结构解体法——从恒载状态开始，拆除所有柔性支承构件(如斜拉索)，释放主梁多余约束，卸除所有外荷载(含自重)，进行几何非线性分析，最终得到梁元的无应力构形.文献[11-12]等在求解构件无应力构形时应用了上述方法.

上述求解方法中，传统单元解体法利用线性或者线性二阶理论作为其分析计算的基础；切线拼装法则是对完整结构进行多次正装迭代进行间接求解；结构解体法则采用类似倒拆原理进行求解.这些求解方法存在需要建立完整的结构分析模型、极大地考验程序几何非线性计算性能及求解精度无法保障等缺点，不能适应现有超大跨度结构精细计算及精细施工控制要求.本文利用非线性二阶梁柱理论及CR-UL全量计算方法，根据已知的结构部分构件的目标构形及外荷载，采用几何法及零作用法直接求解单元的无应力构形基本参数及构件完整无应力构形，克服了上述一般求解方法的缺点(按几何法求解时甚至无需建立结构的有限元模型)，在保证计算精度的基础上加快计算效率.

1 梁元无应力构形基本参数求解

结构(构件)的无应力构形包含其构成单元的无应力构形基本参数(单元曲率及长度)及描述这些独立单元之间相互联接的几何关系.本节基于优化的非线性二阶梁柱理论及CR-UL全量计算理论，建立求解平面梁单元无应力构形基本参数的方法.

1.1 二阶CR梁柱全量计算理论

1.1.1 基于CR旋转坐标的梁柱理论

如图1所示，CR坐标下基于梁柱理论平面梁单元的二阶平衡微分方程(小应变假设[13])如下：

图1 基于CR坐标的梁柱理论Fig.1 Beam-column theory based on Co-rotational procedure

EIy″+MA-QAx-NBy=0

(1)

式中：EI表示单元ij的弯曲刚度;y表示以单元中线描述的横向挠度；l表示单元变形后的弦长；N,Q,M则表示此单元的杆端抗力，该杆端力与位移符号皆按图中标注方向所示,并采用下角标A，B对应单元ij的杆端位置,另外用i表示弯曲线刚度.

式(1)求解得到的转角位移方程最终可用稳定函数表示为[14]：

(2)

式中：θA(B)表示CR坐标下单元全量杆端转角位移.基于式(2)，并依据单元首末端的弯矩平衡方程可确定单元杆端横向力；依据变形前后参数l0(无应力长度)、l并考虑“弓弦效应”可精确计算单元轴向力.文献[14]给出了不考虑剪切效应的具有明确截断准则的适用于-3.8≤NB/NE<(NE为单元的欧拉临界荷载)范围的稳定函数幂级数解，本文亦借鉴其相关公式并对其进行优化：

c1=3+q/20-q2/2 800+R(γ)

(3)

c2=1+jγ2/c1

(4)

R(γ)=3(1+3j)γ6.25-0.75j/40 000

(5)

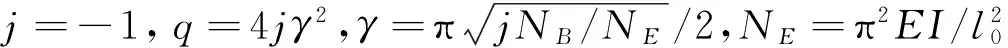
上式中l0表示梁元无应力长度.考虑梁柱构件的“弓弦效应”，则对单元的轴力修正量为[15]：

ΔNB=EACb=EA(b1(θA+θB)2+

b2(θA-θB)2)

(6)

其中：

b1=(s+c)(2-c)/8q,b2=c/(s+c)/8

(7)

上述式中的系数s,c均与单元的轴力相关，且有如下转换关系：

s=c1+c2,c=c1-c2

(8)

当轴力很小(可设定为γ≤1.2e-3)时，有：

b1=1/40,b2=1/24

(9)

经实际编程验证，上述基于梁柱理论的全量非线性分析方法计算效率高，稳定性好.

1.1.2 CR-TL/UL全量计算理论

如图2所示，CR-TL形式的全量求解方法中参考构形与现时构形分别约定为：以单元初始时刻(无应力)所处状态为参考构形，后续t及t+Δt时刻的计算皆以其为基准从而计算全量位移及内力，若需要对各时刻之间的增量求解，则利用不同时刻对应的全量结果进行累减即可得到.

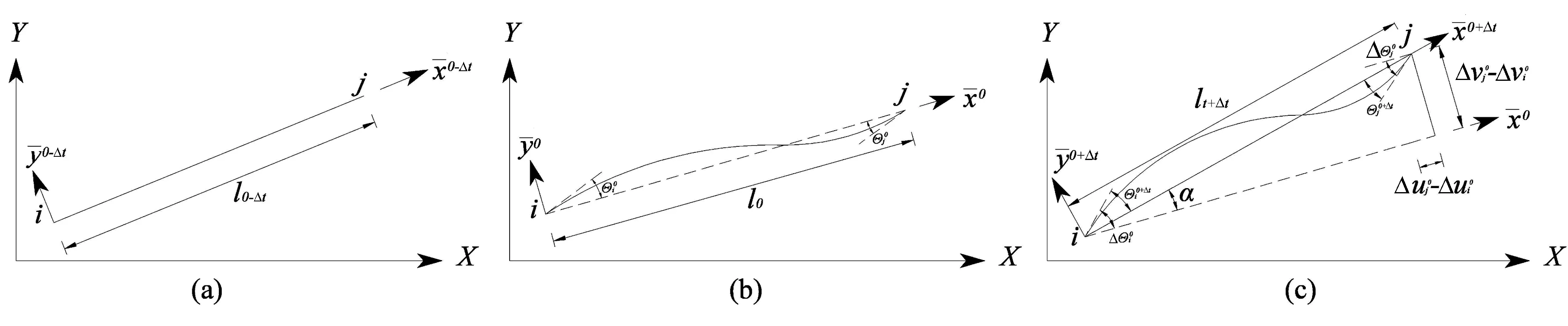
图2 CR-TL/UL坐标系统构成Fig.2 Co-ratational TL/UL procedure system composition

考虑另一种情况：1)已知结构某阶段以单元弦线表示的构形——仅已知控制节点坐标而非完整的连续光滑曲线；2)已知作用于结构的外荷载、结构(构件)单元内力及边界支承力(当仅分析结构的一部分时，可将与该分部结构联系的构件单元内力作为作用在关注结构部分的支承力).这种已知初始状态与一般有限元分析初始状态的差别既是该状态下的梁元具有初始内力及与之相协调的初始杆端转角.依据CR全量梁柱理论，当求解单元局部坐标系下的内力时仅需关注节点发生的累计转角位移(能引起杆端抗力)，而与单元所处的实际位置无关(亦既符合刚体检验[16]).

由此当已知结构目标构形及其对应的内力与边界支承反力，直接求解结构(构件)的无应力构形参数时，初始状态即是上述具有初始内力与初始弯曲构形而非一般求解分析中参考状态0时刻对应的无应力状态.解决此问题的一种思路是假定在此0时刻之前存在一个无应力状态时刻-Δt，而当前的0时刻由此假定状态经全量计算得到，若后续继续进行计算，则可随时更新参考状态，按此更新参考状态的方法属于几何非线性分析的UL法，当其与CR全量计算理论结合后，利用该法(CR-UL)即可进行逆向计算从而求解无应力构形(零作用法)，亦能针对具有初始内力的结构继续进行全量正装计算.

1.2 梁元无应力构形基本参数求解

求解梁元的无应力构形基本参数主要关注两个方面：1)单元无应力曲率——表现为单元首末端的弯曲角；2)单元无应力长度.

1.2.1 梁单元无应力曲率求解

将式(2)反解，得到采用杆端内力表示的单元首末端弯曲角为：

(10)

对于某一给定的无应力长度l0参数，根据单元的弦线长度参数及上述梁柱理论求解公式，可得到最终包含轴力效应的θA,θB值.

1.2.2 梁单元无应力长度求解

将上步求解得到的与单元k无应力长度l0相符的精确轴向力NB与已知的单元轴向力TF比较，假设此两者的绝对误差为：

DN=NB-TF

(11)

修正l0值，且设置DN的收敛精度循环上述步骤即可求解最终真实的无应力长度l0值.实际计算过程中，可采用二分法迭代修正该值，其具体过程简化为：

1)首先确定一般条件下满足无应力长度l0值的可能区间：

l0∈[(1-EP)l,(1+EP)l]

(12)

其中EP可根据材料的屈服应变值确定(例如1/1 000).l为上述根据单元节点坐标确定的有应力弦长值.对于合理设置的EP值，通过二分区间两边界处轴力误差DN的乘积性质，经少量(最多3次)计算即可确定最初的二分区间(见图3(a)).

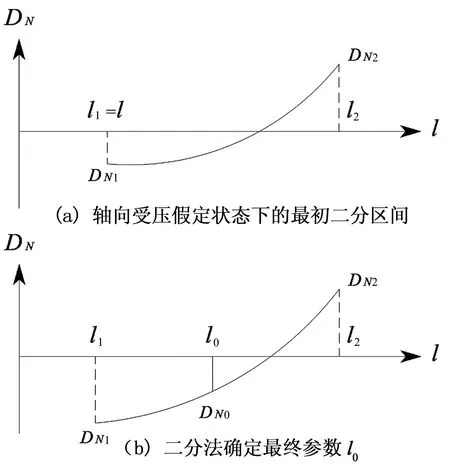
图3 二分法求解l0原理Fig.3 Theory of solving about l0based on dichotomy

2)根据确定的二分区间[l1,l2]，求解与上述区间对应的轴力误差[DN1,DN2]，若轴向力误差不满足收敛精度，则重新二分确定当前更新的无应力长度l0，随后再代入梁柱理论求解公式进行新一轮计算，直到上述的DN收敛条件满足(见图3(b))，最终得到与单元内力一致的无应力构形基本参数.

2 构件单元完整无应力构形求解

2.1 几何法求解梁元完整无应力构形

考察如图4所示的刚架及其在外荷载作用后的变形状态.其中图4(a)示出了初始安装构形(显然是一种无应力构形)及其上作用的荷载；图4(b)示出了目标构形及其与初始安装构形的相对关系；图4(c)～图4(e)则示出了通过目标构形达到无应力构形的几何实现过程；此外图4(f)示出了最终得到的无应力构形与初始安装构形之间的区别是仅存在一个刚体转角(若节点A为固端，则无应力构形与初始安装构形完全重合).以下结合图中刚架释出具体实现过程.

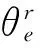
4)按此过程依次对余下单元执行上述过程，即得到所有单元构成的完整无应力构形.

图4 单元解体法求解刚架无应力构形Fig.4 The unstressed configuration solving of rigid frame based on element disintegration theory

其中涉及到的(以平面直杆为例)求解(弦)单元在整体坐标系中绕首节点i转动φ且满足无应力单元长度le0的新坐标计算方法如下．

如图5所示的直杆单元e,f及其目标构形下的几何参数，以单元e为例说明绕其首端点i刚体转动有限弧度φ(逆时针为正且含义见图4)后，末端点新坐标可表述为：

(13)

式中ξe为单元e对应的方向角，如图5所示，且：

(14)

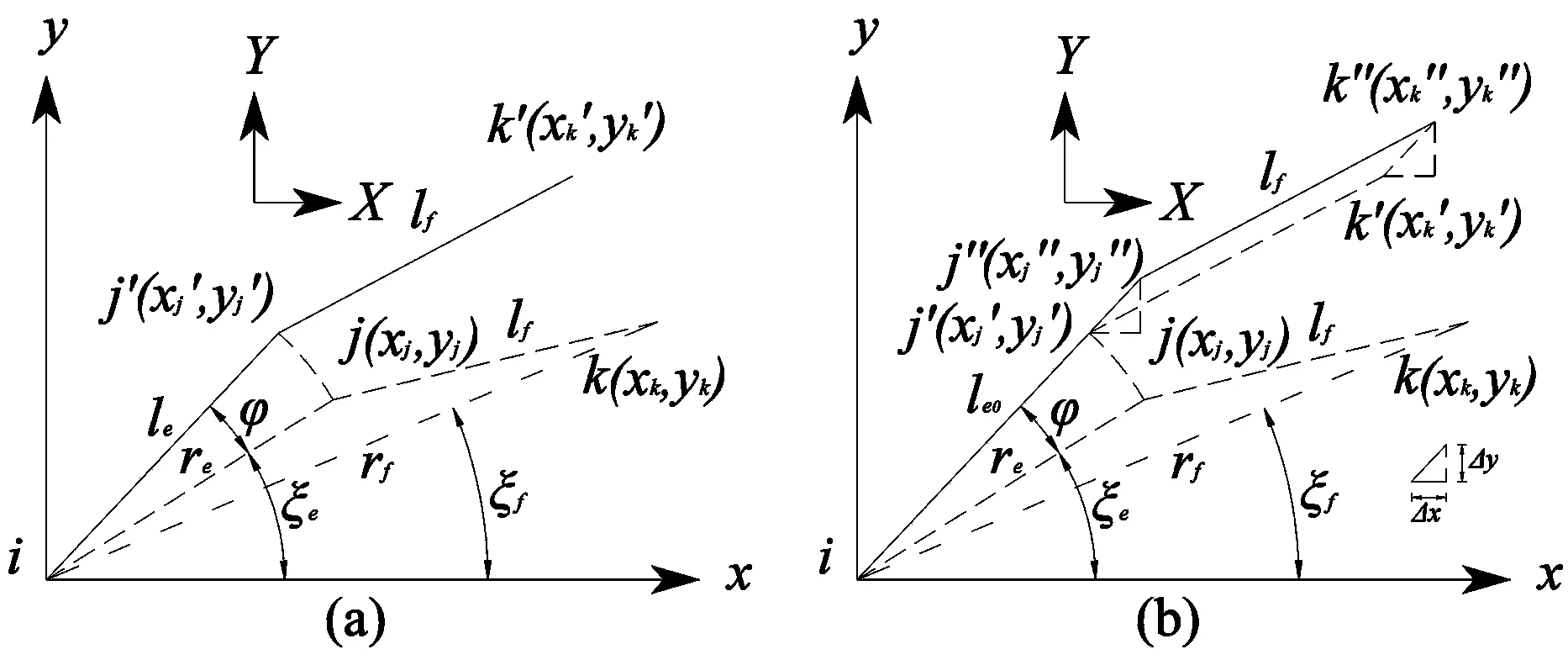
图5 连续单元旋转及平移几何关系Fig.5 The geometric relation of rotation and translation about continuous element

(15)

同时得到坐标迁移量(用于更新后续节点)为：

(16)

据此完成单元e对应坐标的完全更新.对于多单元情况，需在以当前单元首节点i为转心转动时，将所有后续单元皆绕此转心转动更新端点坐标并跟随当前单元同时更新坐标迁移量，逐单元进行上述过程直到完成对所有单元的循环.

根据以上描述可编制求解所有直梁单元无应力构形的子程序.

2.2 零作用法求解梁元完整无应力构形

上节确定的按几何法求解构件无应力构形方法的核心依据既是认为变形前后单元间的夹角(变形后则为单元变形曲线切线之间的夹角)ω保持恒定.但此假定对于采用考虑剪切变形的梁单元来说不适用，因为考虑剪切效应后，节点转角位移将不连续；此外对于首节点为非固端结构体系，得到的无应力构形与原初始安装构形间存在刚体位移差.基于以上原因，可采用下述基于CR-UL全量理论的零作用法，此法仍基于单元解体理论，仅在求解出单元的无应力基本参数后，利用非线性有限元计算理论求解初始安装构形：

1)根据目标构形(例如主梁)划分单元并确定其几何信息；根据确定的求解对象统计其上作用的所有外荷载信息及支承信息．

2)将上述所有外荷载信息转换为直接作用于求解对象节点或单元的荷载信息(例如对于斜拉桥结构则需考虑索元刚臂效应)．

3)按一般结构力学理论生成单元局部CR坐标系下的固端约束力列阵{TF0}及综合节点荷载列阵{P0}，并根据已知的单元内力{TF}求解单元的节点位移杆端力列阵{AF0}．

4)逐单元求解其无应力构形基本参数及局部与整体系下的切线刚度矩阵，准备实现零作用法非线性计算(采用几何法时则直接根据求得的基本参数按前述方法求解无应力构形)．

5)对综合节点荷载逐级卸载(即总加载系数cop自1.0逐渐减小至0.0)：施加新的综合节点荷载值为cop×{P0}→利用切线刚度矩阵计算增量位移→计算不平衡力→更新综合节点荷载列阵{P}及切线刚度矩阵求解增量位移→计算不平衡力→循环直至收敛，最终实现零作用下的结构平衡.

6)得到构件单元的完整无应力构形.

可以看出，两种不同的单元解体理论中，零作用法相对于几何法虽然适应范围更广，但需要编写几何非线性分析程序.

3 考题验证

以下依据上述几何法及零作用法对具有初始内力结构进行无应力构形求解，比较二者的差别，并结合工程实例比较其与传统一般方法求解结果的异同.

3.1 具有初内力(端弯矩)悬臂梁无应力构形求解

如图6所示，具有端弯矩作用的悬臂梁是验证结构发生大位移(含大转角)条件下检验梁单元几何非线性性能的经典算例，本文利用一般求解结果做逆向分析，即将图6中实线所示位形作为目标构型，其对应的内力作为初始内力，将求解得到的无应力构形与图中虚线所示的初始构形进行比较，验证本文计算理论.

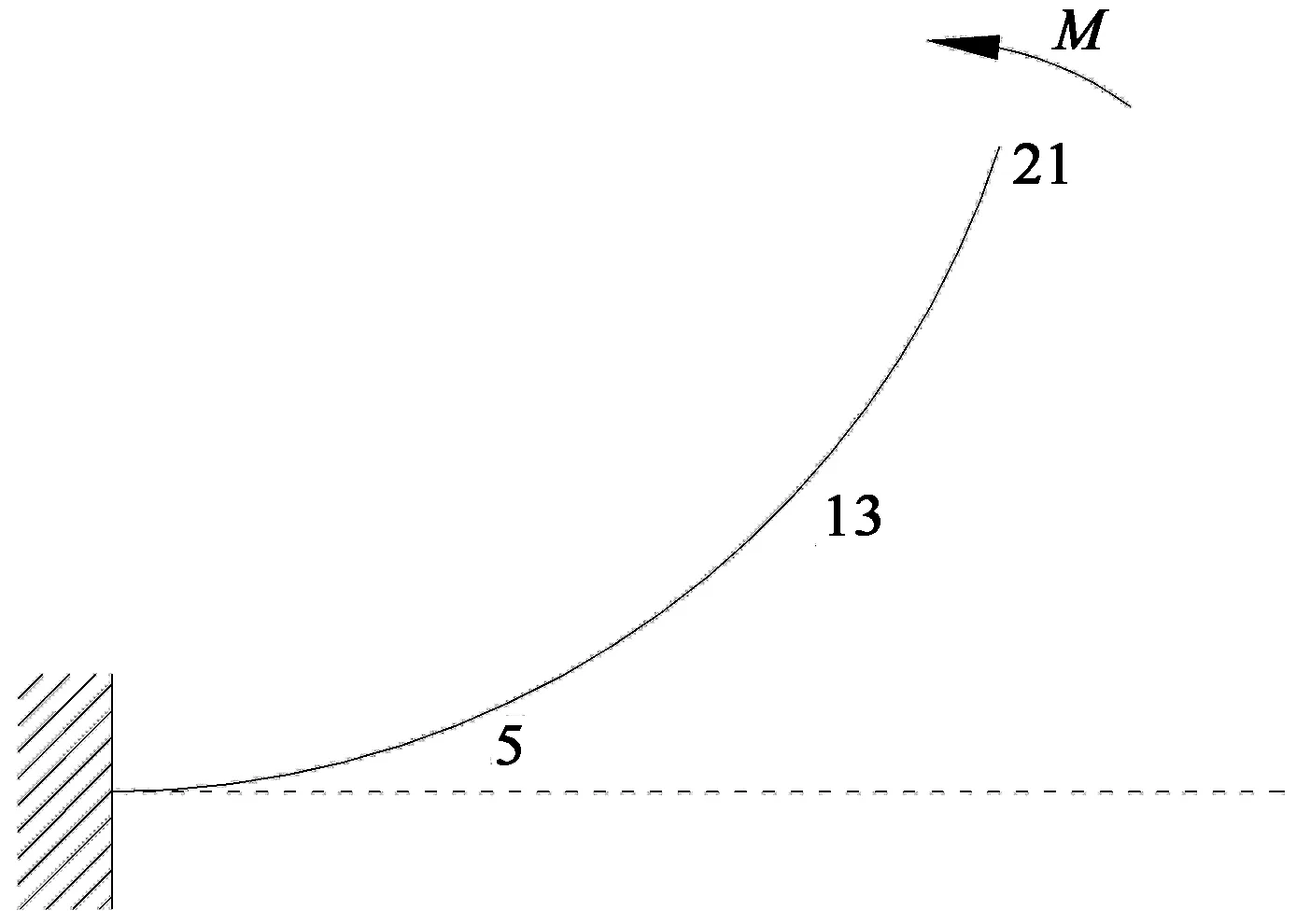
图6 悬臂梁无应力构形求解Fig.6 The unstressed configuration solving of cantilever beam

经典算例中作用端弯矩的悬臂梁结构的计算参数为：原始长度(图6中虚线示出)L=10.0 m，将其划分为20等份，截面面积A=0.06 m2，截面惯性矩I=0.000 2 m4，弹性模量E=2.1E8 kPa，端弯矩M=5 277.875 7 kN·m(自由端转动角为0.2π)，按本文2种方法计算得到无应力构形，并将其与初始构形(图6中虚线示出)比较，其结果见表1(暂不考虑剪切效应影响).

表1 单元解体法计算无应力构形结果比较Tab.1 The result comparison of unstressed configuration solving based on element disintegration theory

理想条件下，求得的无应力构形应如图6中的虚线所示，从上表列出的结果可以看出，采用几何法与零作用法最终对于具有大转动特性梁的无应力求解结果均具有较高的精度，且求解过程表明几何法计算效率更高.

3.2 具有初内力的折线型刚架无应力构形求解

如图7所示的折线型刚架，其计算参数为：长度L=4.0 m，截面面积A=0.01 m2，惯性矩I=0.000 32 m4，弹性模量E=2.0E8 kPa，其上作用荷载值为F=600.0 kN，M=600.0 kN·m，q=300.0 kN/m，此外原结构的边界条件设为i节点铰接，j节点刚接.图中虚线表示荷载作用下的变形图亦即目标构形(示出弦线)，粗实线示出采用几何法求得的无应力构形(仅与原初始构形存在刚体位移差).采用零作用法求得的无应力构形则与原初始构形基本重合，因此图中未再示出.

图7 折线型刚架无应力构形求解Fig.7 The unstressed configuration solving of fold line rigid frame

本算例主要验证平面框架类结构无应力构形求解精度.根据计算结果，采用两种方法求得的无应力构形均很理想，且求解过程亦表明几何法计算效率更高.

3.3 超大跨度斜拉桥主梁无应力构形求解

如图8所示的某跨长江双塔双索面半漂浮结构体系混合梁斜拉桥，南边跨和主跨南索塔附近为混凝土主梁，主跨大部分与北边跨为钢箱梁.现选取整个北塔区钢箱梁，按本文单元解体法求解其无应力构形，并与切线拼装迭代法计算结果进行比较，验证本文相关计算理论的正确性.

图8 某长江公路大桥施工及成桥状态Fig.8 The construction and finished bridge state in certain yangtze river highway bridge

按单元解体法求解梁元无应力构形时，首先根据目标构形(成桥状态)及该构形下的主梁内力与单元固端力求解单元杆端抗力，再利用几何法及零作用法求解主梁完整无应力构形.最终按单元解体法及切线拼装迭代法求得的主梁完整无应力构形对比结果见图9.

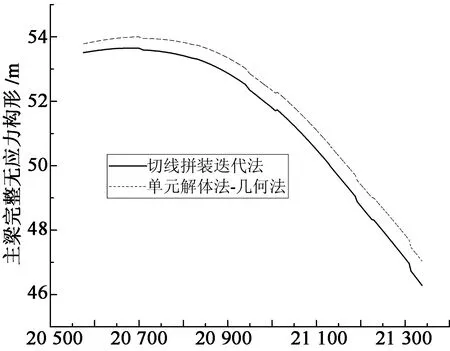
桩号/m图9 超大跨度斜拉桥梁元无应力构形求解Fig.9 The unstressed configuration solving of beam on super long-span cable-stayed bridge

从图9可以看出，按切线拼装迭代法及单元解体法求解得到的主梁无应力构形在整体及局部线形方面皆吻合良好(采用零作用法计算结果与几何法结果基本重合，图中未再示出).实质上，由于此处切线拼装迭代法计入了桥塔结构的压缩及弯曲变形，而单元解体理论则以成桥状态的塔梁交接区作为计算起始点，因此若将图9中采用单元解体法求解得到的完整无应力构形进行刚体平移及转动后，二者是基本重合的两条曲线(经计算两者造成的梁段夹角相对差值为0.003 9%).证明采用单元解体法求解梁元完整无应力构形相关理论的正确性.

4 结 论

根据本文提出的基于单元解体理论的两种精确求解平面梁元无应力构形方法(几何法与零作用法)及与其他方法对比计算结果可知：

1)本文建立的单元解体法能适应平面结构发生大位移(含大转动)情况下的梁元完整无应力构形求解，在保证求解结果精度的同时具有较高的计算效率.

2)采用单元解体法可高效求解平面梁元完整无应力构形，但在特定情况下(如考题3．2中以铰接节点i为求解起始节点；考题3．3中仅取完整桥梁结构的部分构件-主梁)其求解结果与实际初始安装构形存在刚体位移差，但亦是一种精确的制造构形.

3)采用几何法时，无需建立实际结构的大规模有限元模型，仅采用一般结构力学原理及考虑非线性二阶效应的梁柱理论即可精确求解实际结构(或构件)的完整无应力构形，可大量提高工程实施效益；采用零作用时，则需要编写完善的几何非线性分析程序.

[1] 陈芳祖，罗丹. 基于S-R和分解定理的无网格Galerkin法求解几何非线性问题[J]. 湖南大学学报:自然科学版，2012,39(1)：42-46.

CHEN Fang-zu, LUO Dan. Element free Galerkin method for geometrically nonlinear problems based on the S-R decomposition theorem[J]. Journal of Hunan University:Natural Sciences，2012,39(1)：42-46.(In Chinese)

[2] 邓继华，邵旭东. 基于U.L列式的带刚臂平面梁元非线性分析[J]. 湖南大学学报:自然科学版，2012,39(5)：8-12.

DENG Ji-hua， SHAO Xu-dong. Non-linear analysis of plane beam element with rigid arms based on U.L formation[J]. Journal of Hunan University:Natural Sciences，2012,39(5)：8-12. (In Chinese)

[3] 邓继华，邵旭东，张阳,等. 考虑索端刚臂的斜拉桥空间拉索非线性分析[J]. 湖南大学学报:自然科学版，2014,41(1)：21-26.

DENG Ji-hua, SHAO Xu-dong, ZHANG Yang,etal. Non-linear analysis of spatial stay cable with rigid arms of cable-stayed bridge[J]. Journal of Hunan University：Natural Sciences，2014,41(1)：21-26. (In Chinese)

[4] 李文武，潘胜山，张哲,等. 无应力状态有限元法在桥梁竖转施工中的应用[J]. 武汉理工大学学报，2010,32(21)：46-50.

LI Wen-wu, PAN Sheng-shan, ZHANG Zhe,etal. Application of unstressed state method in vertical rotation construction of bridge[J]. Journal of Wuhan University of Technology，2010,32(21)：46-50. (In Chinese)

[5] 王邵锐，周志祥，吴海军. 超大跨自锚式悬索桥施工过程中力学性能的试验研究[J]. 土木工程学报，2014,47(6)：70-77.

WANG Shao-rui, ZHOU Zhi-xiang, WU Hai-jun. Experimental study on the mechanical performance of super long-span self-anchored suspension bridge in construction process[J]. China Civil Engineering Journal，2014,47(6)：70-77. (In Chinese)

[6] 卫少阳. 基于CR列式的无应力状态控制法基本方程[J]. 应用数学与力学，2014,35(12)：1352-1362.

WEI Shao-yang. Basic equations of the unstressed state control method Based on co-rotational formulation[J]. Applied Mathematics and Mechanics，2014,35(12)：1352-1362. (In Chinese)

[7] 秦顺全. 桥梁施工控制——无应力状态法理论与实践[M]. 北京：人民交通出版社，2007：30-40.

QIN Shun-quan. Bridge construction control——theory and practice of unstress stage method[M]. Beijing: China Communications Press,2007：30-40. (In Chinese)

[8] 陈常松，颜东煌，陈政清. 带刚臂的两节点精确悬链线索元的非线性分析[J]. 工程力学，2007,24(5)：29-34.

CHEN Chang-song, YAN Dong-huang, CHEN Zheng-qing. Nonlinear analysis of two-node accurate catenary cable element with arbitary rigid arms[J]. Engineering Mechanics，2007,24(5)：29-34. (In Chinese)

[9] 梁鹏，肖汝诚，徐岳. 超大跨度斜拉桥的安装构形与无应力构形[J]. 长安大学学报:自然科学版，2006,26(4)：49-53.

LIANG Peng, XIAO Ru-cheng, XU Yue. Assembled geometry and unstrained geometry of super long span cable stayed bridge[J]. Journal of Chang’an University:Natural Science Edition，2006,26(4)：49-53. (In Chinese)

[10]YIU P K A, BROTTON D M. Computation of fabrication dimensions for cable stayed bridges[J]. The Structure Engineer, 1998，66(15)：237-243.

[11]赵俊钊，陈务军，付功义,等. 充气膜结构零应力态求解[J]. 工程力学，2012,29(12)：134-140.

ZHAO Jun-zhao, CHEN Wu-jun, FU Gong-yi,etal. The algorithm of zero-stress state of pneumatic stressed membrane structure[J]. Engineering Mechanics，2012,29(12)：134-140. (In Chinese)

[12]李传习，王琛，董创文,等. 基于相位变换的顶推曲梁自适应无应力构形控制[J]. 中国公路学报，2014,27(2)：45-53.

LI Chuan-xi, WANG Chen, DONG Chuang-wen,etal. Control of self-adaptive unstressed configuration for incrementally launched curved girder bredge base on phase transformation[J]. China Journal of Highway and Transport，2014,27(2)：45-53. (In Chinese)

[13]李国强，沈祖炎. 钢结构框架体系弹性及弹塑性分析与计算理论[M]. 上海：上海科学技术出版社，1998：7-13.

LI Guo-qiang, SHEN Zu-yan. Elastic and elastoplastic analysis and computing theory of steel frame system[M]. Shanghai:Science and Technology Press,1998：7-13. (In Chinese)

[14]宋启根，罗穆勇，宋丹. 框架分线性分析的新梁柱单元[J]. 力学季刊，2001,22(2)：186-191.

SONG Qi-gen, LUO Mu-yong, SONG Dan. A new beam-column element for nonlinear analysis of frames[J]. Chinese Quarterly of Mechanics, 2001,22(2)：186-191. (In Chinese)

[15]童根树. 钢结构的平面内稳定[M]. 北京：中国建筑工业出版社，2005：25-42.

TONG Gen-shu. In-plane stability of steel structure[M]. Beijing: China Architecture & Building Press,2005：25-42. (In Chinese)

[16]YANG Y B, LIN S P, CHEN C S. Rigid body concept for geometric nonlinear analysis of 3D frames, plates and shells based on the updated lagrangian formulation[J]. Computer Methods in Applied Mechanics and Engineering, 2007,196: 1178-1192.

Accurate Solution for Unstressed Configuration of Beam by Element Disintegration Theory

DONG Dao-fu1,2，CHEN Chang-song2†，YAN Dong-huang2，TU Guang-ya2，YUAN Ming2

(1. Hunan Province University Key Laboratory of Bridge Engineering, Changsha Univ of Science & Technology, Changsha, Hunan 410114, China; 2. School of Civil Engineering and Architecture, Changsha Univ of Science & Technology, Changsha, Hunan 410114, China;)

In order to solve the unstressed configuration of beams, the accurate computation element disintegration theory, named as geometric method and zero-loads method, was created based on the theory of nonlinear second order beam-column theory and CR-UL total deformation theory. The basic parameters of unstressed configuration of beam were firstly solved by using the geometric information and corresponding element resistance of the objective configuration. The full unstressed configuration of component element was also confirmed by using the geometric method as coordinate transformation. The zero-loads method as converse calculation based on these basic parameters was then proved to be effective. Moreover, a program was compiled to verify the above two methods. The results show that the geometric method for full unstressed configuration of beam elements in this paper could be executed efficiently without the finite element model of full structures, and the zero-loads method could be executed efficiently under the condition of impeccable geometric nonlinear program.

geometric nonlinear; unstressed configuration; element disintegration theory; geometric method; zero-loads method; CR-UL total deformation theory

1674-2974(2016)11-0112-08

2015-11-04

国家自然科学基金资助项目(51178059, 51178058，51678070),National Natural Science Foundation of China (51178059, 51178058，51678070); 国家重点研究基础发展计划(973计划)资助项目(2015CB057706); 长沙理工大学桥梁工程湖南省高校重点实验室开放基金资助项目(13KA03);湖南省教育厅资助科研项目(10K006)

董道福(1984-)，男，湖南张家界人，长沙理工大学博士研究生†通讯联系人，E-mail:changsongchen@vip.sina.com

U441

A