阻尼器对悬索桥吊索扭转振动控制效果的数值研究

李寿英，王世峰，陈政清

(湖南大学 风工程与桥梁工程湖南省重点实验室，湖南 长沙 410082)



阻尼器对悬索桥吊索扭转振动控制效果的数值研究

李寿英†，王世峰，陈政清

(湖南大学 风工程与桥梁工程湖南省重点实验室，湖南 长沙 410082)

刚性分隔器对悬索桥吊索各索股的相对振动可起到很好的控制效果，但吊索可能会发生较大的整体振动，包括平动和扭转振动.采用ANSYS有限元软件，以某桥的四索股吊索为工程背景，分别建立了3种索股-刚性分隔器-阻尼器计算模型，并进行了自由振动分析，研究了理想状况下的吊索扭转模态的无量纲阻尼比曲线特征，研究了阻尼器支架刚度、阻尼器刚度对阻尼器效率的影响.研究结果表明，四索股-刚性分隔器-阻尼器体系不同扭转模态的无量纲阻尼比曲线不重合，不同扭转模态的阻尼器设计不能采用同一条无量纲阻尼比曲线进行设计；随着阻尼器支架刚度的减小，能实现的最优扭转模态阻尼比减小，对应的最优阻尼系数也减小；随着阻尼器刚度的增大，能实现的最优扭转模态阻尼比减小，对应的最优阻尼系数线性增大.

悬索桥；吊索；阻尼器；振动控制；扭转模态

随着悬索桥跨径的增大，吊索的长度也不断增长，其频率低、质量轻、阻尼小，极易在风荷载或车辆荷载的作用下发生大幅振动[1-2].目前世界上最大跨径的前3座悬索桥的吊索均发生过大幅振动，其振动机理有待于进一步的研究.对于单根索而言，在索端安装阻尼器可以起到较好的控制效果，Kovacs[3]最早研究了阻尼器对单根索的控制效果；Pacheco和Fujino[4]则提出了单根索的“统一近似曲线”，明确地给出了系统阻尼比与阻尼器阻尼系数的关系；Krenk[5]提出了“统一近似曲线”的解析式；在此基础上，很多学者对拉索刚度、阻尼器刚度以及阻尼器支架刚度等的影响进行研究[6-9].实践结果也表明[10]，阻尼器对单根索的振动控制可以达到很好的控制效果.但是，悬索桥吊索常由多根索股组成，常见的形式有2,3,4根，人们尝试在吊索之间安装阻尼器进行振动控制，但已有的研究结果表明，控制效果不是很好[11]，这一特点在多分裂导线的振动控制中也被证实[12].多座悬索桥(如丹麦大海带东桥、我国西堠门大桥)吊索的振动控制的经验表明，在索股之间安装刚性分隔器可以起到很好的控制效果[11].但是，在索股之间安装刚性分隔器时，吊索的整体振动(包括平动和扭转)可能会成为其主要振动形式.阻尼器对于吊索整体平动的控制效果与单根索类似，可参照已有的单根索研究成果进行阻尼器设计.本文以我国西堠门大桥吊索的四索股体系为工程背景，采用数值方法，进行了索股-刚性分隔器-阻尼器体系的自由振动分析，研究了阻尼器对四索股-刚性分隔器系统扭转振动的控制效果，并对阻尼器支架刚度、阻尼器刚度的影响进行了参数研究.

1 计算模型

为方便安装和维护，阻尼器安装在吊索近梁端位置，这与斜拉索的情况类似.在斜拉索上安装阻尼器时，一个锚固点上安装两个阻尼器，阻尼器平面与拉索轴向垂直，但两个阻尼器之间呈一定角度，以同时控制斜拉索面内和面外的振动.与斜拉索不同的是，为控制悬索桥四吊索的扭转振动，需在不同索股上平行安装两个阻尼器.

采用3种不同的计算模型对悬索桥吊索的四索股-刚性分割器-阻尼器体系进行自由振动分析，如图1所示.其中，模型1为理想状况，仅考虑阻尼器的阻尼系数的影响，阻尼器支架刚度为无穷，阻尼器刚度为零；模型2考虑阻尼器支架刚度的影响，阻尼器刚度为零；模型3考虑阻尼器刚度的影响，阻尼器支架刚度为无穷.图1中，T为索股张力；L为索股长度；M为索股单位长度质量；cl为单位长度上结构阻尼系数；xc为阻尼器安装点与拉索锚固点的距离；c为阻尼器阻尼系数；kz为阻尼器支架刚度；kc为阻尼器刚度.考虑阻尼器支架刚度影响时，阻尼元件和弹簧元件串联(模型2)；考虑阻尼器刚度影响时，阻尼元件和弹簧元件并联(模型3).

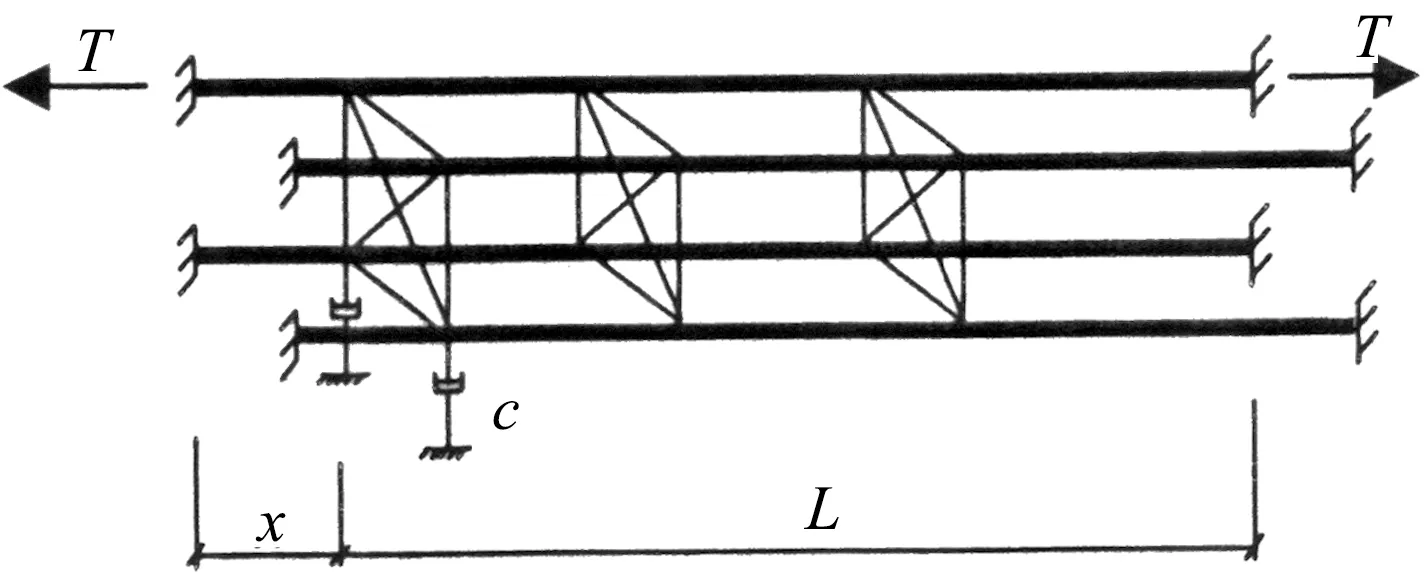
(a) 模型1

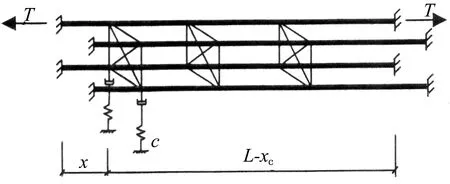
(b) 模型2

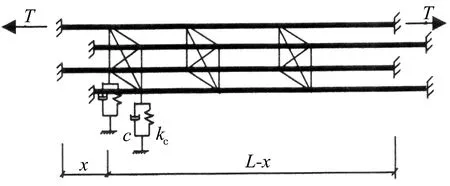
(c) 模型3图1 计算模型示意图Fig.1 Sketch map of computational models

计算在ANSYS软件平台上进行，采用BEAM4单元模拟悬索桥吊索；LINK10单元模拟刚性分隔器；COMBIN14单元模拟阻尼器和弹簧单元，该单元可以设置阻尼系数和刚度系数.以国内某桥的一根吊索为例进行研究，该吊索长度为166 m，设计索力为922 kN，质量线密度为25 kg/m，单根索股一阶模态频率为0.57 Hz，顺桥向和横桥向的索股间距分别为0.4 m和0.6 m.在该吊索上设置4个等间距的刚性分隔器，根据风洞试验及现场实测结果[9]，这种形式的分隔器布置可有效控制索股相对运动.另外，为保证阻尼器控制吊索整体振动的效率，在阻尼器安装位置也设置刚性分隔器.

2 无量纲阻尼比曲线

首先采用模型1研究扭转模态阻尼比与阻尼器阻尼系数的关系，这两个参数均采用无量纲形式，以下简称“无量纲阻尼比曲线”.图2给出了四索股-刚性分隔器-阻尼器体系的第1和2阶扭转模态的无量纲阻尼比曲线，其横、纵坐标分别采用无量纲量c/(MLω01)·i·xc/L和ξi/(xc/L)表示，其中，ω01是第1阶平动频率，i为扭转模态阶数.当然，ω01也可以取第1阶扭转频率，这里取第1阶平动频率主要是为了在相同参数的基础上与单根索的结果进行比较.从图2中可以看出，四索股-刚性分隔器-阻尼器体系扭转模态的无量纲阻尼比曲线具有明显的最优值，这与平动模态无量纲阻尼比曲线相同.其中，第1,2阶扭转模态的最优无量纲阻尼比分别为0.49和0.42，对应的最优无量纲阻尼器阻尼系数分别为0.73和0.78.另外，从图2还可以看出，不同扭转模态的无量纲阻尼比曲线不重合，这与平动模态无量纲阻尼比曲线几乎完全重合的结果有明显的差异[4].因此，对于悬索桥吊索-刚性分隔器体系的扭转振动控制，其阻尼器的设计要考虑这一特点.

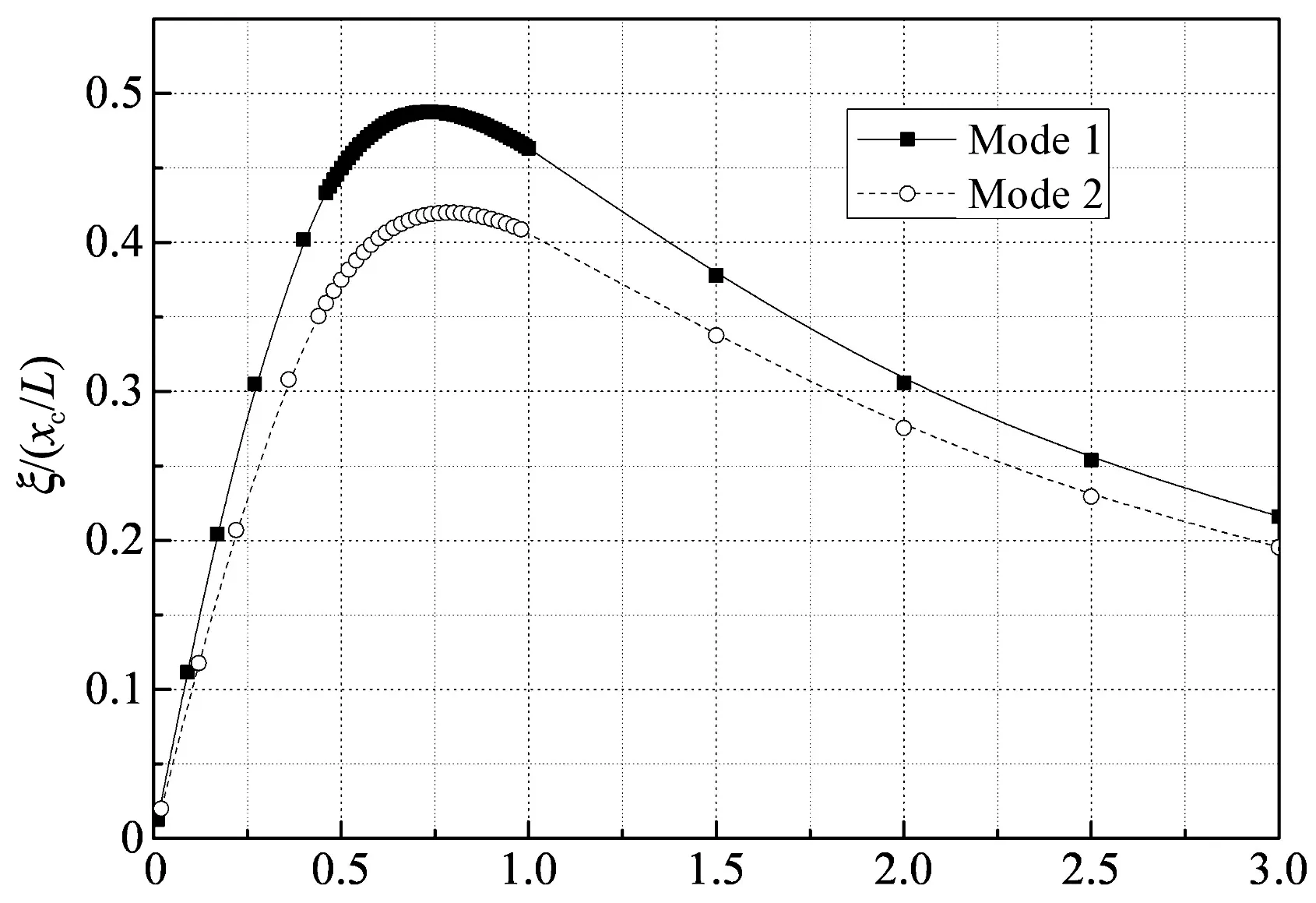
[c/(MLω01)]i(xc/l)图2 前2阶扭转模态的无量纲阻尼比曲线Fig.2 Universal curve of the first two torsional modes

图3给出了第1阶扭转模态和第1阶平动模态的无量纲阻尼比曲线的对比.从图3中可以看出，第1阶扭转和平动模态的最优无量纲阻尼比基本相同，均为0.49，但第1阶扭转模态对应的最优无量纲阻尼器阻尼系数(0.73)要大于第1阶平动模态的值(0.36).两条曲线大约交于c/(MLω01)·i·xc/L=0.50处，此时第1阶扭转和第1阶平动的模态阻尼比均能达到0.46.当c/(MLω01)·i·xc/L<0.50，第1阶平动模态阻尼比大于第1扭转模态阻尼比；反之，则第1平动模态阻尼比小于第1阶扭转模态阻尼比.因此，如需对第1阶扭转模态和第1阶平动模态均达到较好的控制效果，进行阻尼器设计时，可取无量纲阻尼器阻尼系数为0.5.需要说明的是，图3中的平动模态无量纲阻尼比曲线与文献结果[2]有区别，特别是最优无量纲阻尼系数的位置，这主要是c和M取值、结构体系的差异造成的.

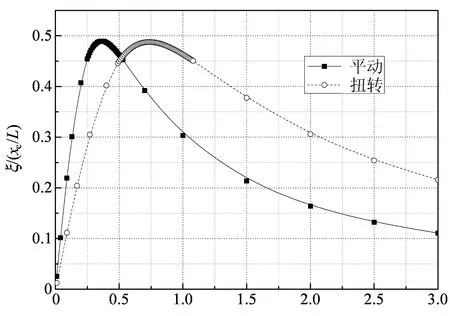
[c/(MLω01)]i(xc/l)图3 第1阶扭转和平动模态无量纲阻尼比曲线的比较Fig.3 Comparison between the universal curves of the first torsional and translational modes

3 阻尼器支架刚度的影响

采用模型2研究阻尼器支架刚度对阻尼器效率的影响，此时阻尼器与弹簧串联，该研究的目的是为合理的阻尼器支架刚度设计提供理论参考.采用无量纲参数uz=kzxc/T表示阻尼器支架刚度.图4给出了阻尼器支架刚度uz=500,100,50和20时前2阶扭转模态的无量纲阻尼比曲线.

从图4中可以看出，当阻尼器支架刚度足够大时(如uz=500)，第1和2阶扭转模态最优无量纲阻尼比分别为0.49和0.42，这与阻尼器刚度为无穷大时一致(如图2所示).当阻尼器支架刚度减小，第1和2阶扭转模态的最优无量纲阻尼比也减小，例如，当uz=100,50,20时，对应的第1阶扭转模态最优无量纲阻尼比分别为0.43,0.38和0.29，第2阶扭转模态最优无量纲阻尼比分别为0.37,0.33和0.25.另外，随着支架刚度的减小，最优无量纲阻尼器阻尼系数也减小，例如，当uz=100,50,20时，对应的第1阶扭转模态最优无量纲阻尼器阻尼系数分别为0.66,0.60和0.48，第2阶扭转模态最优无量纲阻尼器阻尼系数分别为0.70,0.65和0.48.图5给出了阻尼器支架刚度uz=∞，500,100,50,20时第1阶扭转模态无量纲阻尼比曲线的比较.从图5中可以明显地看出最优无量纲阻尼比和最优无量纲阻尼器阻尼系数随着阻尼器支架刚度的上述变化规律.

[c/(MLω01)]i(xc/l) (a) uz=500

[c/(MLω01)]i(xc/l) (b) uz=100

[c/(MLω01)]i(xc/l) (c) uz=50

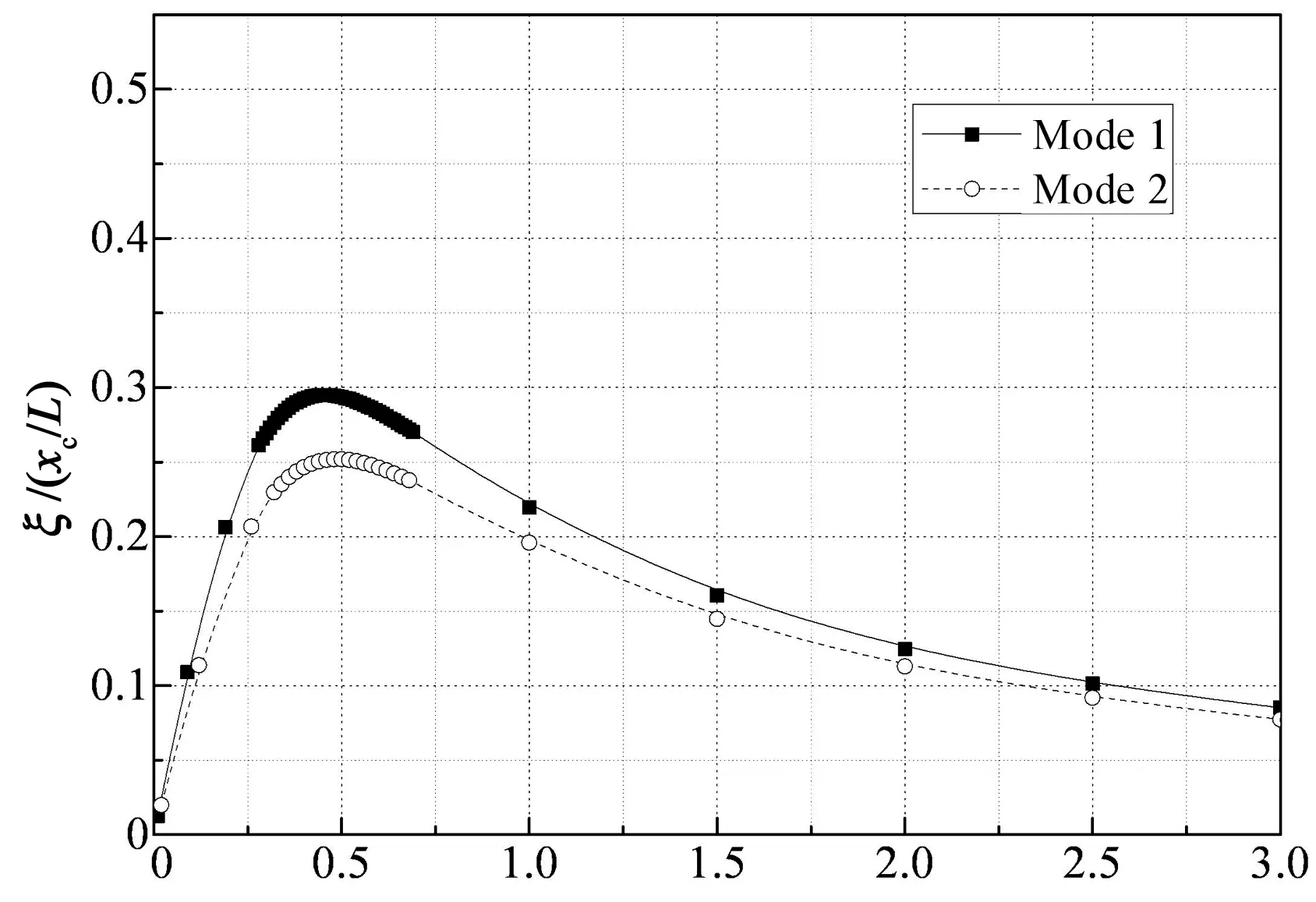
[c/(MLω01)]i(xc/l) (d) uz=20图4 不同阻尼器支架刚度时的前2阶扭转模态无量纲阻尼比曲线Fig.4 Universal curves of the first two torsional modes with different support stiffness

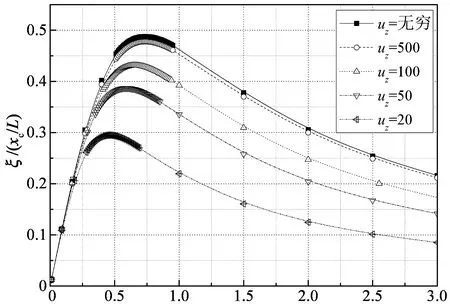
[c/(MLω01)]i(xc/l)图5 不同阻尼器支架刚度时的第1阶 扭转模态无量纲阻尼比曲线的比较Fig.5 Comparison of the universal curves of the first torsional mode with different support stiffness

图6(a)和(b)分别给出了第1阶和第2阶扭转模态最优无量纲阻尼比和最优无量纲阻尼器阻尼系数随阻尼器支架刚度的变化规律.从图6中可以看出，当阻尼器支架刚度不足时，阻尼器的效率减小，且实现最优阻尼比的最优阻尼系数减小，也就是说，为了达到最优阻尼比，阻尼器阻尼系数应比理想状态的值小.图6的结果可为阻尼器支架刚度的设计提供定量的参考.

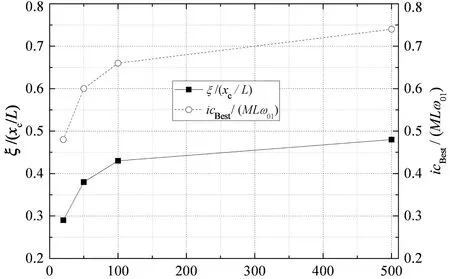
Kixc/T(a) 第1阶扭转模态

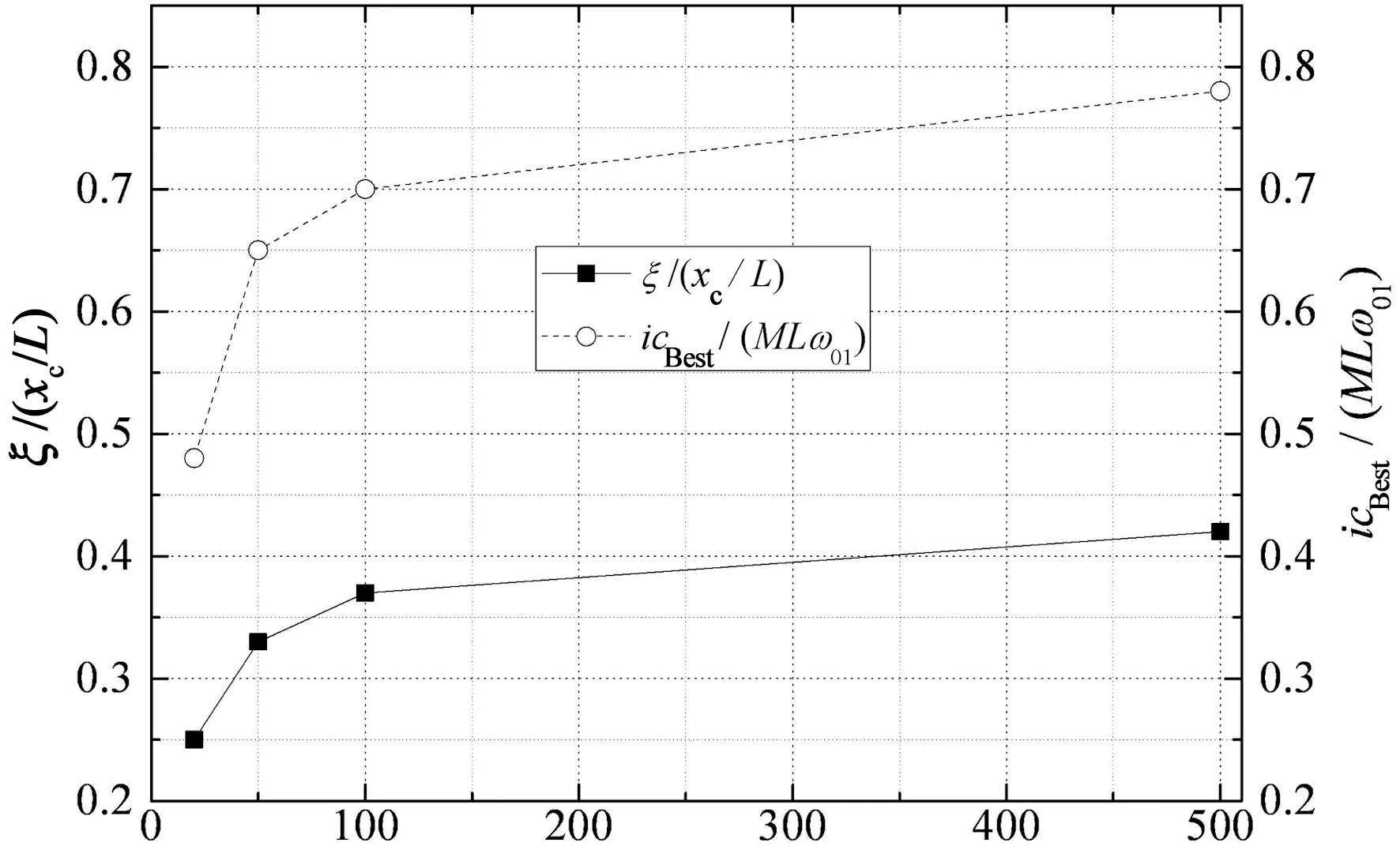
Kixc/T(b)第2阶扭转模态图6 最优阻尼比和阻尼系数随支架刚度变化曲线Fig.6 Variations of the maximum damping ratio and corresponding damping coefficient with support stiffness

4 阻尼器刚度的影响

采用模型3研究阻尼器刚度对阻尼器效率的影响，此时阻尼器与弹簧并联.与阻尼器支架刚度无量纲化方式类似，采用无量纲参数uc=kcxc/T来表示阻尼器刚度.图7给出了阻尼器刚度uc=0.1,1,5和10时第1和2阶扭转模态的无量纲阻尼比曲线，横、纵坐标的无量纲定义与前文相同.

从图7中可以看出，当阻尼器刚度足够小时(如uc=0.1)，第1和2阶扭转模态最优无量纲阻尼比分别为0.49和0.42，与阻尼器刚度为零时的结果相同(如图2所示)，此时阻尼器刚度对阻尼器效率基本无影响.随着阻尼器刚度的增加，最优无量纲阻尼比减小.例如，当阻尼器刚度uc=1,5和10时，第1阶扭转模态最优无量纲阻尼比分别为0.45,0.35和0.27，第2阶扭转模态最优无量纲阻尼比分别为0.39,0.30和0.23.另外，随着阻尼器刚度的增加，最优无量纲阻尼器阻尼系数也增大.例如，当阻尼器刚度uc=1,5和10时，第1阶扭转模态最优无量纲阻尼器阻尼系数分别为0.79,1.01和1.25，第2阶扭转模态最优无量纲阻尼器阻尼系数分别为0.84,1.06和1.38.因此，如果阻尼器具有较大的刚度，需要适度增加阻尼器阻尼系数以实现最优的阻尼器效

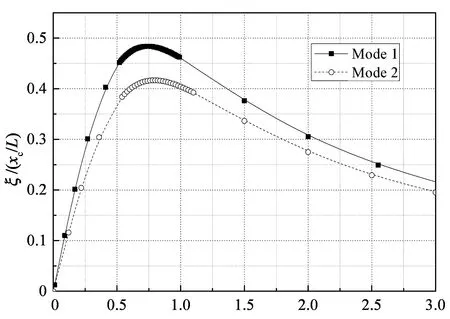
[c/(MLω01)]i(xc/l) (a) uc=0.1

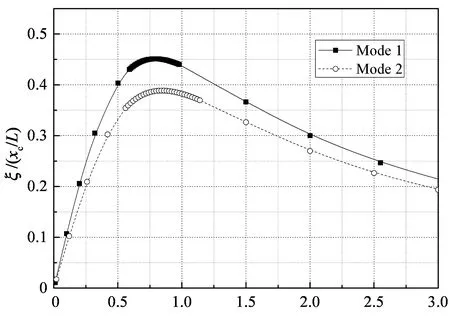
[c/(MLω01)]i(xc/l) (b) uc=1

[c/(MLω01)]i(xc/l) (c)uc=5

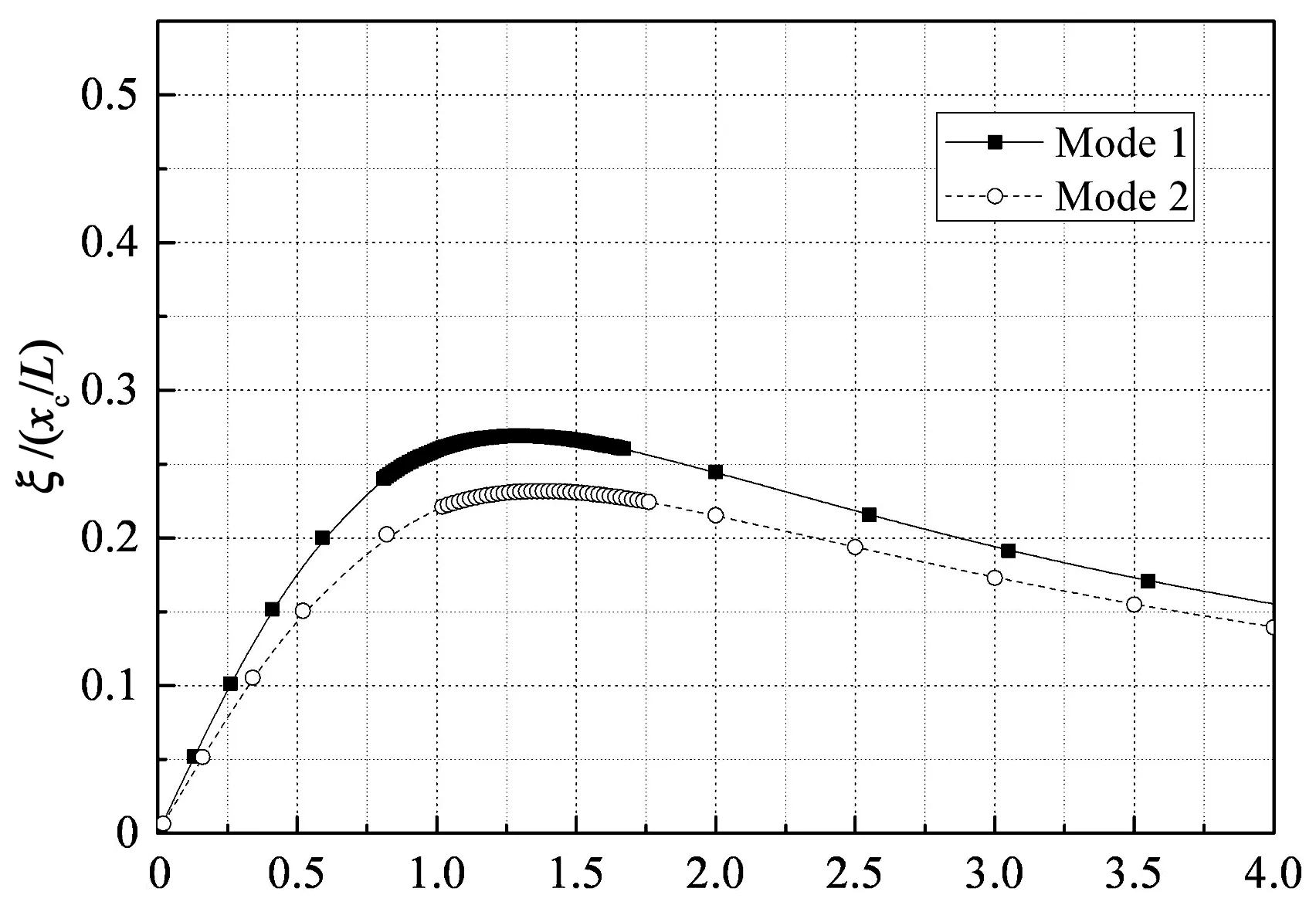
[c/(MLω01)]i(xc/l) (d) uc=10图7 不同阻尼器刚度时前2阶扭转 模态无量纲阻尼比曲线Fig.7 Universal curves of the first two torsional modes with different damper stiffness

率.图8给出了不同阻尼器刚度时第1阶扭转模态无量纲阻尼比曲线的比较.从图8中可以明显看出最优无量纲阻尼比和最优无量纲阻尼器阻尼系数随着阻尼器刚度的上述变化规律.

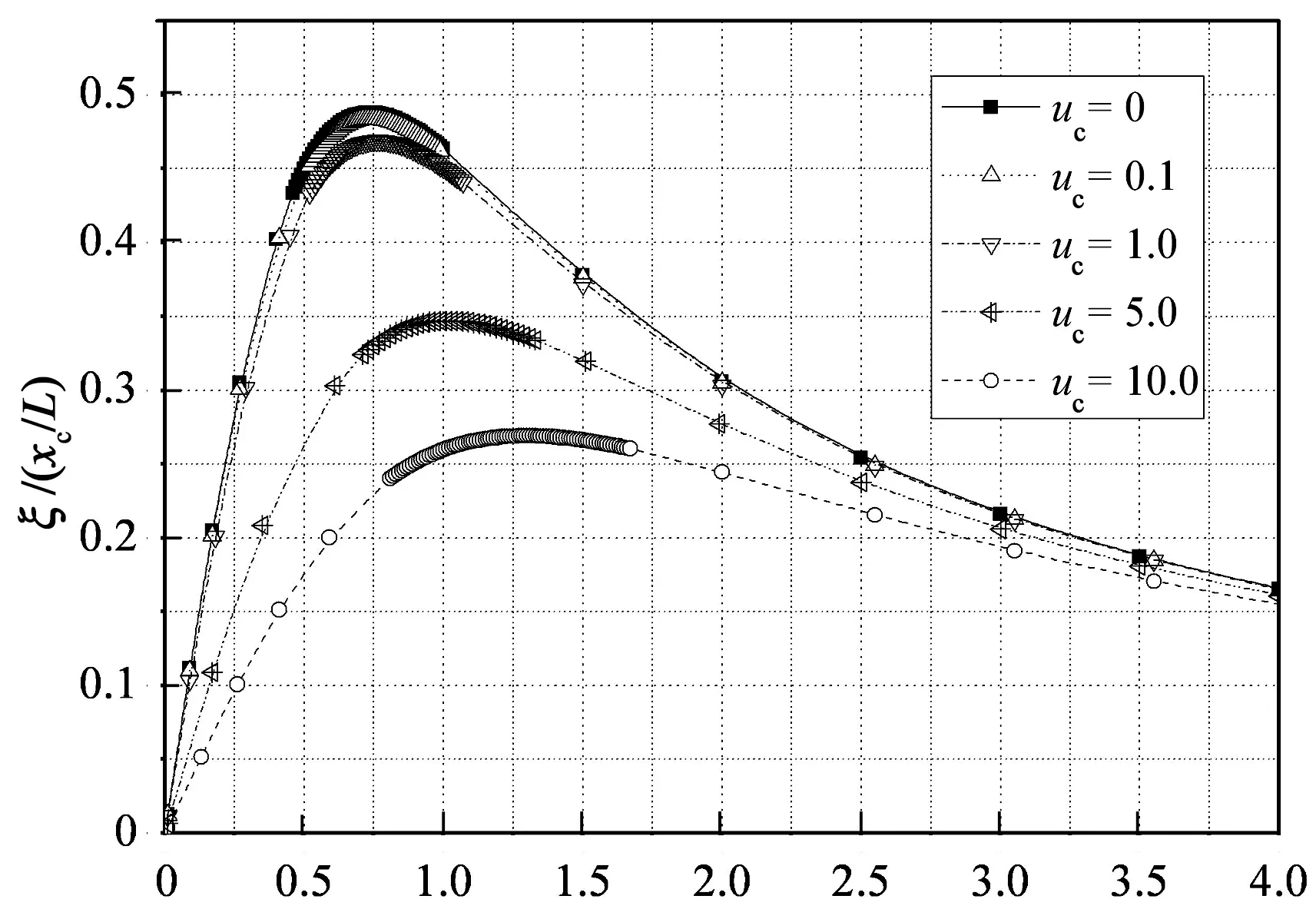
[c/(MLω01)]i(xc/l)图8 不同阻尼器刚度时第1阶扭转 模态无量纲阻尼比曲线的比较Fig.8 Comparison of universal curves of the first torsional mode with different damper stiffness

图9给出了第1和2阶扭转模态最优无量纲阻尼比和最优无量纲阻尼器阻尼系数随阻尼器刚度的变化规律.从图9中可以看出，若阻尼器存在刚度，为实现最优阻尼比，阻尼器阻尼系数应比理想状态的值大，这一点与阻尼器支架刚度的影响是相反的.另外，从图9中还可以看出，最优阻尼器阻尼系数与阻尼器刚度基本上呈线性关系.

Kixc/T(a) 第1阶扭转模态

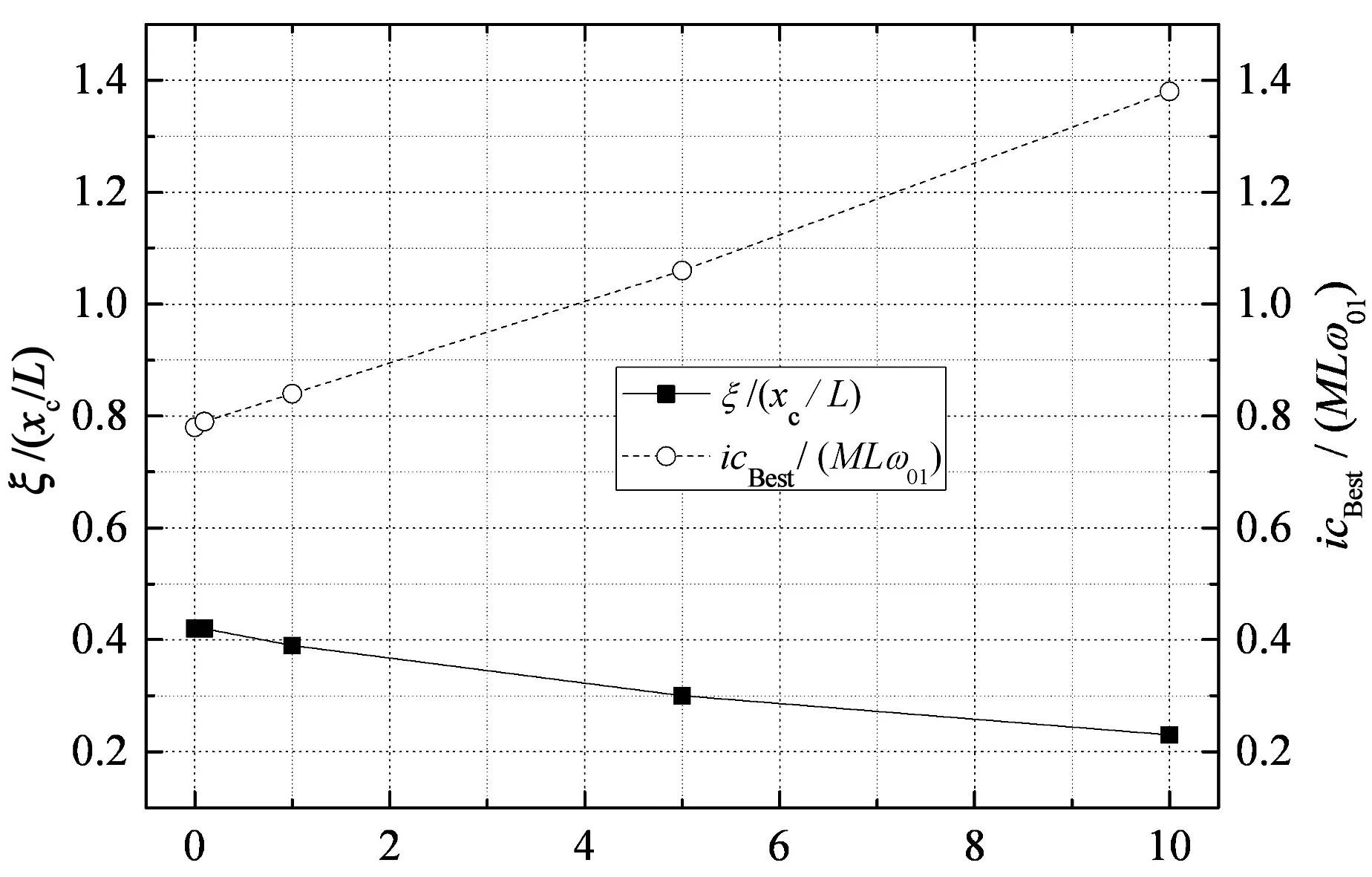
Kixc/T(b)第2阶扭转模态图9 最优阻尼比和阻尼系数随阻尼器刚度变化曲线Fig.9 Variations of the maximum damping ratio and corresponding damper coefficient with damper stiffness

5 结 论

采用大型通用有限元软件ANSYS建立悬索桥吊索的四索股-刚性分隔器-阻尼器模型，研究了悬索桥吊索整体扭转模态的无量纲阻尼比曲线，并对阻尼器支架刚度和阻尼器刚度的影响进行参数研究，得出如下结论：

1) 采用阻尼器对悬索桥吊索-刚性分隔器体系的整体扭转模态进行振动控制时，不同扭转模态无量纲阻尼比曲线不一致，这与平动模态的结果不同.研究结果表明，高阶扭转模态的最优阻尼比小于低阶模态的值.

2)随着阻尼器支架刚度的减小，能实现的最优扭转模态阻尼比减小，最优阻尼系数也减小.

3)随着阻尼器刚度的增大，能实现的最优模态阻尼比减小，最优阻尼系数线性增大.

[1] 陈政清,雷旭,华旭刚,等.大跨度悬索桥吊索减振技术研究与应用[J].湖南大学学报:自然科学版,2016, 43(1): 1-10.

CHEN Zheng-qing, LEI Xu, HUA Xu-gang,etal. Research and application of vibration control mechod for hanger cables in long-span suspension bridge[J]. Journal of Hunan University: Natural Sciences, 2016, 43(1): 1-10.(In Chinese)

[2] 张志田,吴肖波,葛耀君, 等.悬索桥吊索风致内共振及减振措施初探[J].湖南大学学报:自然科学版,2016, 43(1): 11-19.

ZHANG Zhi-tian, WU Xiao-bo, GE Yao-jun,etal. Wind induced internal resonance and the control method of suspension bridge hangers[J]. Journal of Hunan University : Natural Sciences, 2016, 43(1): 11-19. (In Chinese)

[3] KOVACS I. Zur frage der seilschwingungen und derseildampfung[J]. Die Bautechnik, 1982, 59(10): 325.

[4] PACHECO B M, FUJINO Y, SULEKH A. Estimation curve for modal damping in stay cables with viscous damper[J]. Journal of Structural Engineering, 1993, 119(6): 1061-1079.

[5] KRENK S. Vibrations of a taut cable with an external damper[J]. Journal of Applied Mechanics-Transactions of the ASME, 2000, 67(4):772.

[6] TABATABAI Habib, MEHRABI Armin B. Design of mechanical viscous dampers for stay cables[J]. Journal of Bridge Engineering,2000, 5(2):114-123.

[7] MAIN Joseph A, JONES Nicholas P.Vibration of tensioned beams with intermediate viscous damper II: Damper near a support[J]. Journal of Structural Michanics, 2007, 133(4): 379-388.

[8] 周海俊,孙利民.斜拉索附加带刚度阻尼器的参数优化分析[J].力学季刊,2008,29(1): 180-185.

ZHOU Hai-jun,SUN Li-ming.Parameter optimization of damper with stiffness for stay cable[J]. Chinese Quarterly of Mechanics, 2008, 29(1): 180-185. (In Chinese)

[9] 周海俊,丁炜,孙利民.拉索-阻尼器-弹簧系统的阻尼特性分析[J].工程力学，2014, 31(1):79-84.

ZHOU Hai-jun, DING Wei, SUN Li-ming. Damping of taut cable with a damper and spring[J]. Engineering Mechanics, 2014, 31(1): 79-84. (In Chinese)

[10]CHEN Zheng-qing, HUA Xu-gang, KO J M,etal. MR damping system for mitigating wind-rain induced vibration on Dongting Lake cable-stayed bridge[J].Wind and Structures, 2004, 7(5): 293-304.

[11]陈政清，华旭刚，王建辉，等. 西堠门悬索桥吊索振动观测与减振措施研究报告[R]. 长沙：湖南大学土木工程学院，2015.

CHEN Zheng-qing, HUA Xu-gang, WANG Jian-hui,etal. Report for the vibration survey and vibration control measure of hangers of Xihoumen Bridge[R]. Changsha: College of Civil Engineering, Hunan University, 2015. (In Chinese)

[12]PRICE S J, PIPERNI P.An investigation of the effect of mechanical damping to alleviate wake-induced flutter of overhead power conductors[J]. Journal of Fluids and Structures, 1988, 2(1): 53-71.

Numerical Study on the Mitigation of Torsional Vibration of the Hangers of Suspension Bridges by Using Dampers

LI Shou-ying†, WANG Shi-feng, CHEN Zheng-qing

(Key Laboratory of Wind and Bridge Engineering of Hunan Province, Hunan Univ, Changsha, Hunan 410082，China)

The relative oscillation between the strands of the suspension bridge hangers could be effectively mitigated by means of rigid spacers, but the hanger-spacer system may experience overall translational or torsional vibrations. In this paper, based on a four-strand hanger of the Xihoumen Bridge, the ANSYS software was utilized to establish three kinds of computational models for the hanger-spacer-damper system, and a series of free vibration analyses were carried out to study the characteristics of the universal curve for the torsional modes considering the effects of support stiffness and damper stiffness. The results show that the universal curves are affected by the torsional modes, and a unified universal curve cannot be used for the design of the dampers for different torsional modes. The realizable maximum damping ratio for torsional mode and its corresponding damper coefficient reduce with the decrease of the support stiffness. However, the realizable maximum ratio for torsional mode decreases with the increase of the damper stiffness, but its corresponding damper coefficient increases.

suspension bridges; hangers; dampers; mitigation of vibration; torsional mode

1674-2974(2016)11-0007-06

2015-11-20

国家自然科学基金资助项目(51578234), National Natural Science Foundation of China(51578234)；国家重点基础研究发展计划(973计划)项目(2015CB057700)

李寿英(1977-)，男，江西萍乡人，湖南大学副教授，博士，博士生导师†通讯联系人，E-mail: shyli@hnu.edu.cn

TU973.3

A