青少年日常体力活动摄氧量预测方程的建立和检验*

周铁成，王 海，朱 琳

(1.电子科技大学中山学院体育部,广东 中山 528403；2. 哈尔滨工业大学体育部，黑龙江 哈尔滨 150000；3.广州体育学院运动与健康系，广东 广州 510500)



青少年日常体力活动摄氧量预测方程的建立和检验*

周铁成1，王 海2，朱 琳3*

(1.电子科技大学中山学院体育部,广东 中山 528403；2. 哈尔滨工业大学体育部，黑龙江 哈尔滨 150000；3.广州体育学院运动与健康系，广东 广州 510500)

目的：建立更适合我国青少年的，更经济、有效的日常体力活动摄氧量方法。方法：90名11～14岁青少年随机分成实验组(60人)和验证组(30人)，男女各半。实验组以3～8km/h速度进行6个速度级别的逐级递增跑台运动，每级运动5min；以COSMED K4b2的测量值为因变量，以周岁年龄、性别、身高、体重、BMI、体脂率、瘦体重为自变量，建立回归方程；验证组在自由状态下进行运动，通过配对样本T检验用以检验预测方程的有效性，采用Bland-Altman法用于检验预测方程在自由状态下预测摄氧量的系统偏差。结果：自建的预测方程为Y(mL/min)=15.404×负荷心率+23.514×体重(kg)-194.592×性别-1735.307；男性=1，女性=2；方程R2=0.601，SEE=398.15，F检验P<0.001，说明自变量与因变量存在线性关系，方程的拟合程度较高；自变量回归系数和常数项t检验，P<0.001，说明自变量回归系数和常数项有意义，回归模型可靠。自建的预测方程和李海燕预测方程与实测值间均无显著性差异(P>0.05)，自建的预测方程(男R=0.728，P<0.001；女R=0.603，P<0.001)与实测值存在中度相关，且相关系数均高于李海燕预测方程(男R=0.636，P<0.001；女R=0.568，P<0.001)；所建预测方程95%的残差均落在Bland-Altman图±1.96SD区间内，表明方程有较好的预测能力。结论：自建摄氧量预测方程有效，比同类摄氧量预测方程更经济、有效，更适用于青少年的日常体力活动摄氧量的预测。

青少年；摄氧量；日常体力活动；预测方程

能量消耗是机体任何活动过程中所伴随的能量的存储、释放、转移和利用；而这其中需要氧的参与，因此常用摄氧量及其相关指标来反映机体的能量消耗水平。机体单位时间内，摄取并被实际消耗或利用的氧量即被称为摄氧量。

青少年并不是成年人的简单缩小。研究显示，儿童的静息能量消耗和单项活动的体力活动能量消耗均高于成年人；有学者研究发现，男孩子在走、跑活动的能量消耗要大于成年男性[1-3]；年龄越小的儿童在进行走、跑活动时的相对摄氧量与成年人的差距最大[4-7]，但随着年龄的增加这种差距会缩小，意味着儿童走、跑的相对摄氧量会随着年龄的增加而下降。朱琳等学者研究发现，随着年龄的增加男女体力活动相对摄氧量普遍下降，但不同年龄组间均无显著性差异。为此，对于青少年摄氧量的研究不能应用成年人的研究成果，同时研究应集中在有限的年龄范围。

本文利用能量消耗研究的金标准法——气体代谢分析法，建立适用于青少年的能量消耗预测方程，并用Bland-Altman法检验实测值与预测方程预测值的一致性，以评价常用预测预测方程的估算效果，试图找到一种经济、非介入式的日常体力活动能量消耗测量的方法。

1 研究对象和研究方法

1.1 研究对象

研究共招募90名11岁～14岁周岁学生，分成实验组(60人)和验证组(30人)，男女各半；实验组用于摄氧量预测方程的建立，验证组用于预测方程有效性的检验。所有参加者均身体健康，没有参与过系统的运动训练。样本基本情况见表1。

表1 受试者基本信息 (xTX-±s)

指标实验组男性(N=30)女性(N=30)验证组男性(N=15)女性(N=15)周岁年龄(y)1310±0921296±0921297±0951302±098身高(m)166±008157±006165±009160±004体重(kg)5793±9774814±9375429±10935283±835BMI(kg/m2)2100±2851956±2941995±3282180±480体脂率(%)2085±5992398±4701676±6032524±515瘦体重(kg)4567±7143629±5464489±7593916±391

1.2 研究方法

1.2.1 COSMED K4b2便携式气体代谢分析仪

利用间接测热原理设计的COSMED K4b2(Rome，Italy)已经公认为是测定机体能量消耗的“金标准”[8]，能有效测量各种运动强度下的摄氧量[9]，常作为能量消耗测量的校标方法。实验提取原始指标VO2(ml/min)和心率。

1.2.2形态指标测量

采用学生体质规范测量仪器和方法对身高、体重进行测量，并计算身体质量指数BMI；用日本TANITA身体成分分析仪测量体脂率，并计算瘦体重(痩体重=体重×(1-体脂率)。

1.2.3 实验安排

餐后1h以上，实验组在坡度为0的跑台上完成3～8km/h的持续走、跑实验。其中，3、4、5、6km/h分别代表慢走、轻松步行、正常步行、快走；7、8km/h分别代表慢跑和快跑；每个速度运动5min，共计30min。验证组在自由状态下以4～7km/h进行走跑运动30min。

1.2.4 数据统计分析

所有数据均用±s表示，数据的统计分析用SPSS 16.0完成。采用配对样本T检验，检验实测值与方程预测值差异性，P <0.05为差异有统计学意义；逐步回归法建立预测方程；Bland-Altman法分析预测方程的系统偏差，确定实测值与方程预测值的一致性。

2 研究结果

2.1 摄氧量预测方程的建立

实验组以K4b2实测能耗值为因变量，以周岁年龄、性别、身高、体重、BMI、体脂率、瘦体重为自变量，通过逐步回归的方法获得预测方程Y(mL/min)=15.404×负荷心率+23.514×体重(kg)-194.592×性别-1735.307；男性=1，女性=2。方程R2=0.601，SEE=398.15，F检验P<0.001，说明自变量与因变量存在线性关系，方程的拟合程度较高；自变量回归系数和常数项t检验，P<0.001，说明自变量回归系数和常数项有意义。

2.2 摄氧量预测方程的验证

从验证组(详见表2)的检验可知，实测值与本文自建的预测方程(P>0.05)、李海燕所建预测方程(P>0.05)比较，均不存在显著性差异；实测值与两个方程均存在中度相关；其中，无论男性还是女性，自建的预测方程(男R=0.728，P<0.001；女R=0.603，P<0.001)与实测值的相关系数均高于李海燕预测方程(男R=0.636，P<0.001；女R=0.568，P<0.001)。

本文利用Bland-Altman方法，对实测值与本文自建的预测方程的预测值和李海燕预测方程的预测值的一致性分析表明(详见图1，图2)，本文自建的预测方程的预测值与实测值间的残差均在95%的一致性界限(男性-782.507～548.3031ml/min；女性-513.472～439.6213ml/min)；李海燕所建女性预测方程的预测值与实测值残差部分超过95%的一致性界限(-754.848～52.754ml/min)，李海燕所建男性预测方程的预测值与实测值残差在95%的一致性界限(-1060.16 ～104.4336ml/min)。

注：李海燕预测方程为：摄氧量(mL/min)=17. 24×负荷心率+8. 76×瘦体重(kg)-1288. 22(男性)；摄氧量(mL/min )=18. 72×负荷心率+5.61×瘦体重(kg)-1588.79(女性)。实测值与预测值的相关分析，***为p<0.001。

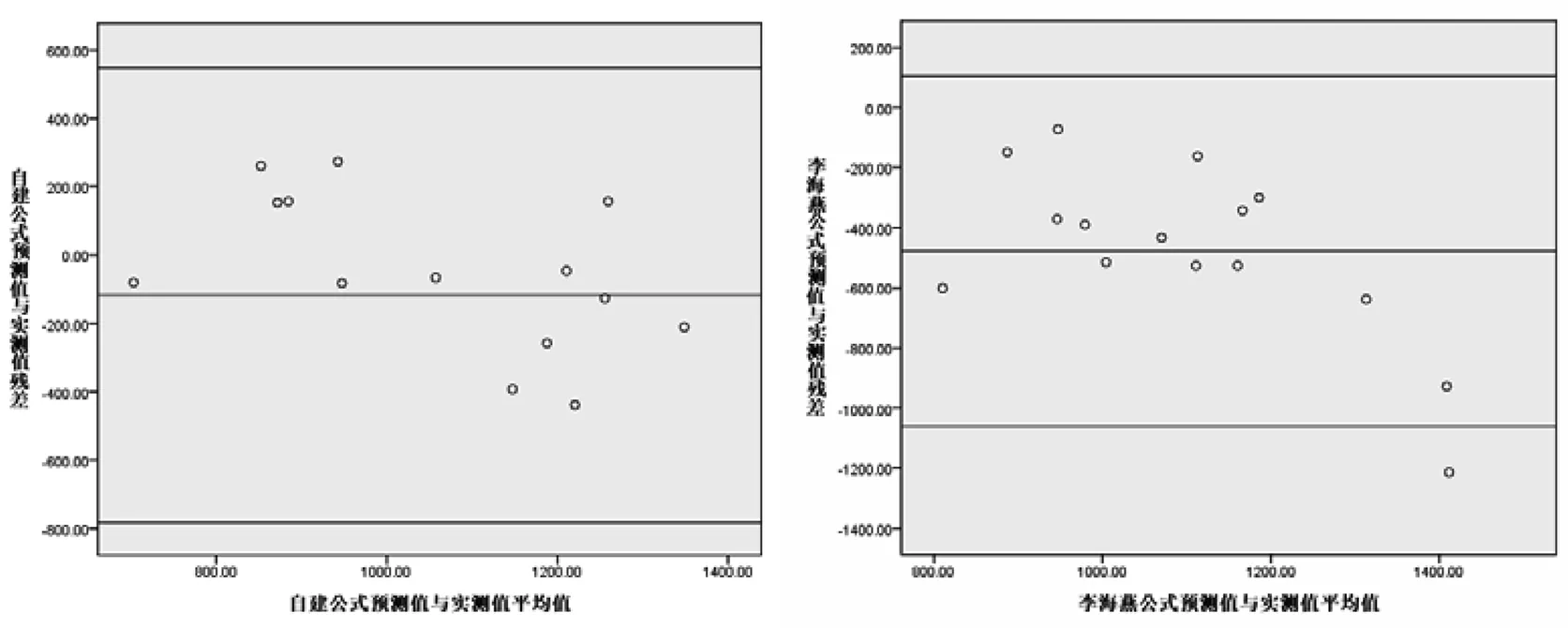
图1 预测方程的Bland-Altman散点图(男性)

图2 预测方程的Bland-Altman散点图(女性)

3 分析与讨论

体力活动(也有人称之为即身体活动)即由骨骼肌收缩造成能量消耗增加的身体动作[11]。在日常生活中，走、跑是最为常见的活动形式，对于青少年，3～8km/h的速度分别代表慢走、轻松步行、正常步速、快走、慢跑和快跑。双标水法和间接测热法已被公认是能量消耗测量的“金标准”法[12, 13]，COSMED K4b2(以下简称K4b2)是基于开放式循环间接测热原理设计的能量消耗测量仪，目前已经广泛应用于儿童和青少年的能量消耗测量的研究中[14, 15]，本文运用K4b2作为能量消耗测量的校标法是可靠的。

健康人群能量消耗(摄氧量)受年龄、性别、身高、体重、内分泌、气候等因素的影响。本文以K4b2实测的摄氧量为因变量，以周岁年龄、性别、身高、体重、BMI、体脂率、瘦体重为自变量，通过逐步回归分析法建立预测方程，最终负荷心率、体重、性别作为自变量因素进入预测方程，显示摄氧量与负荷心率、体重、性别存在线性关系；所建预测方程R2=0.601(p<0.001)，说明因变量的60.1%的变异可以由自变量解释，方程的拟合程度较高；自变量回归系数和常数项t检验，P<0.001，说明自变量回归系数和常数项有意义，所建预测方程成立。本文自建的预测方程的自变量为负荷心率、体重、性别；李海燕预测方程自变量为负荷心率和瘦体重(R2判定系数男生为0.80,女生为0.84)，瘦体重的获得需要借助体成分分析仪，在获得体脂率的基础上才能够推算出瘦体重，所以日常生活中人们很难获得瘦体重这项指标。因此，相比较而言本文所建预测方程的自变量更容易获得，预测方程更经济、方便。

日常生活中，极低速的走以及极快速的跑都是不常见的[16]，当在地面以低于15. 6 km/h的速度进行走跑运动时，所产生的能量消耗略高于在跑台上的运动(p>0.05)，但并不存在统计学意义[10, 17]。为此，本文以4～7km/h的自由走跑运动作为日常体力活动的主要表现形式，用以验证预测方程的有效性。研究显示，自建的预测方程和李海燕预测方程与实测值均表现为中度相关，但自建的预测方程的相关系数均高于李海燕预测方程。Bland-Altman的一致性分析表明，实测值与自建回归方程的预测值间，残差的95%均落在±1.96SD区间内，表明本文自建的预测方程的预测值与实测值间有较好的一致性，两种方法可以互相替代；李海燕预测方程在女性的预测中不够理想。可见，相比而言本文所建预测方程更有效。

4 结论

本研究应用线性回归分析的方法，建立的以负荷心率、体重、性别为自变量的摄氧量预测方程有效，能有效监测11～14岁青少年自由状态下的摄氧量；自建的预测方程比同类摄氧量预测公式更经济、有效，更适用于青少年的日常体力活动的摄氧量预测。

[1] Harrell J S, Mcmurray R G, Baggett C D, et al. Energy costs of physical activities in children and adolescents[J]. Med Sci Sports Exerc. 2005, 37(2): 329-336

[2] Cooke C B, Mcdonagh M J, Nevill A M, et al. Effects of load on oxygen intake in trained boys and men during treadmill running[J]. J Appl Physiol. 1991, 71(4): 1237-1244

[3] Geissler G, Aldouri M. Racial differences in the energy cost of standardized activities[J]. Ann Nutr Metab，1985(29): 40-47

[4] 王明田. 12～15歲國中生走路與跑步的能量消耗[D].台湾：國立體育大學碩士論文，2004

[5] Montoye H J. Age and oxygen utilization during submaximal treadmill exercise in males[J]. J Gerontol. 1982, 37(4): 396-402

[6] Waters R L, Hislop H J, Thomas L, et al. Energy cost of walking in normal children and teenagers[J]. Dev Med Child Neurol. 1983, 25(2): 184-188

[7] Sallis J F, Buono M J, Freedson P S. Bias in estimating caloric expenditure from physical activity in children. Implications for epidemiological studies[J]. Sports Med. 1991, 11(4): 203-209

[8] 朱琳，陈佩杰. 三轴运动加速度计(GT3X)测量青春期少年(11～14岁)身体活动能耗预测方程的建立和检验[J]. 中国体育科技，2013, 50(3): 73-77

[9] Trost S G, Way R, Okely A D. Predictive validity of three ActiGraph energy expenditure equations for children[J]. Med Sci Sports Exerc. 2006, 38(2): 380-387

[10] 李海燕，陈佩杰，庄洁. 青少年体力活动摄氧量预测方法的实验研究[J]. 上海预防医学，2011, 23(7): 321-324

[11] 杨锡让. 实用运动生理学[M]. 北京: 北京体育大学出版社, 2007: 293

[12] Scagliusi F B, Ferriolli E, Lancha A J. Underreporting of energy intake in developing nations[J]. Nutr Rev. 2006, 64(7): 319-330

[13] Roberts S B. Use of the doubly labeled water method for measurement of energy expenditure, total body water, water intake, and metabolizable energy intake in humans and small animals[J]. Can J Physiol Pharmacol. 1989, 67(10): 1190-1198

[14] Schmitz K H, Treuth M, Hannan P, et al. Predicting energy expenditure from accelerometry counts in adolescent girls[J]. Med Sci Sports Exerc. 2005, 37(1): 155-161

[15] Treuth M S, Schmitz K, Catellier D J, et al. Defining accelerometer thresholds for activity intensities in adolescent girls[J]. Med Sci Sports Exerc. 2004, 36(7): 1259-1266

[16] 戴剑松，孙飙，沈洪兵. 加速度传感器测量体力活动的应用综述[J]. 中国运动医学杂志，2009(6): 720-727

[17] Frishberg B A. An analysis of overground and treadmill sprinting[J]. Med Sci Sports Exerc. 1983, 15(6): 478-485

Establishing and Verifying the Prediction Equation of the Teenagers' Daily Physical Activities Oxygen Consumption

ZHOU Tie-cheng1, WANG Hai2, ZHU Lin3*

(1.Department of P.E., Zhongshan Institute, University of Electronic Science and Technology of China, Zhongshan 528403, China;2 Department of Physical Education, PHarbin Institute of Technology, Harbin 150000, China;3 Department of Sport and Health, Guangzhou Sport University, Guangzhou 510500, China)

Purpose: This study aims at establishing an economical and effective equation suitable for the measurement of the Chinese teenagers' oxygen consumption when doing their daily physical activities. Methods: 90 teenagers between the age of 11 to 14 were divided into two groups: the experimental (60) and the validation (30), and each group was evenly composed of males and females. The experimental group was tested by a 6-speed-grades incremental load treadmill exercise with the beginning speed of 3～8km/h and each grade lasting for 5 minutes. A regression equation was established regarding the measured values of Cosmed K4b2 as dependent variables and the ages, sexes, heights, weights, BMI, body fat rate and lean body mass as the independent variables. The validation group exercised in normal conditions and the effectiveness of the prediction equation was verified by the paired-samples T test, while the Bland-Altman method was applied to check the systematic deviation of the oxygen consumption of the prediction equation in normal conditions. Results: The prediction equation can be written as: Y(mL/min)=15.404×load heart rate+23.514×weight(kg)-194.592×sex-1735.307；The Male=1，The Female=2；Equation R2=0.601，SEE=398.15，F Verification P<0.001， There is no significant difference(P>0.05)between the prediction equation established and Li Haiyan's. There is a moderate correlation between this prediction equation(For the male R=0.728，P<0.001；For the female R=0.603，P<0.001) and the measured values and the correlation coefficient is higher than Li Haiyan's (For the male R=0.636，P<0.001；For the female R=0.568，P<0.001). 95% residuals of this prediction equation are distributed in the ±1.96SD section of the Bland-Altman graph, which indicates the better predictive ability of this equation. Conclusion: The prediction equation established for oxygen consumption is valid, which is more economical and effective than the similar ones and more suitable for the prediction of teenagers' oxygen consumption when doing their daily physical activities.

teenager; oxygen consumption; daily physical activities; prediction equation

2016-10-08

周铁成(1979-)，男，本科，黑龙江省哈尔滨人，讲师 通讯作者：朱琳(1975-)，女，汉族，博士，教授，博导

教育部人文社会科学青年基金项目(13YJC890050)阶段研究成果；广东省科技计划项目(2014A020220010)资助

G804

A

1007-323X(2016)06-0093-04

研究方向：体育教学