基于Allan方差改进阈值的惯性传感器动态信号小波去噪*

朱战辉，张友妮，汪立新，曲云星

（1.火箭军工程大学，西安710025；2.中国人民解放军96401部队，陕西宝鸡721006）

基于Allan方差改进阈值的惯性传感器动态信号小波去噪*

朱战辉1，2，张友妮2，汪立新1*，曲云星2

（1.火箭军工程大学，西安710025；2.中国人民解放军96401部队，陕西宝鸡721006）

惯性传感器信号的去噪效果通常都是用Allan方差来评价，针对这个特点，提出了一种基于Allan方差噪声系数的小波阈值改进算法。先用提升小波将信号分解到不同频段，再用Allan方差计算各频带上的噪声系数，根据各频带噪声系数的大小确定其滤波阈值，再结合参数可调的阈值函数对各尺度信号进行滤波去噪。改进算法以去噪效果评价参数来修正阈值，具有很强的针对性。通过同其它常用的惯性传感器去噪方法做比较，证明该算法可以有效的随机噪声，提取出更加准确真实的惯性传感器动态输出。

惯性传感器；动态信号；小波阈值去噪；Allan方差；噪声系数

惯性传感器作为惯性导航系统（INS）的核心部件之一，温度、振动、冲击和磁场等环境的变化都会影响其输出的准确性。导弹和飞机等惯性传感器载体经常工作在高动态环境下，因此如何消除和减小惯性传感器的动态误差，成为提高导航精度的重要环节［1-2］。惯性传感器的误差通常分为常值误差和随机误差（随机噪声），常值误差可以通过硬件或者系统级标定去除，随机漂移受环境因素影响，表现出时变与弱非线性，很难建立起理想的数学模型。因此，采取合适的数据滤波算法对动态条件下惯性传感器随机漂移误差进行去噪处理，对于提高惯导系统精度，具有重要的研究意义。

惯性传感器的噪声去除多采用建立陀螺随机误差模型的方法，基于所建立的误差模型利用Kal⁃man等滤波技术来消除噪声的影响。如果建立的误差模型与实际偏差较大将严重影响系统的滤波精度甚至导致滤波的发散［3］。然而在动态条件下，陀螺信号具有时变、非平稳、非线性的特点，很难获得精确的误差模型。而平滑滤波、中值滤波等时域滤波方法，对频率分布复杂的信号很难取得理想效果。小波变换在时域和频域都有优良的局部化特性，不需要建立精确的随机误差模型，非常适用于处理陀螺的动态输出信息［4］。

小波阈值去噪是一种实现简单且效果较好的去噪方法，实现该方法的关键是阈值的选取。对于动态信号，频率成分复杂，信号先验信息未知，如果不能确定合适的阈值，会导致高频有用信号丢失或噪声部分保留过多的情况发生。文献［5］通过对均方差函数渐进寻优的方式寻找最优阈值，对动态条件下的光纤陀螺输出信号进行去噪，取得了很好的效果。但迭代寻优算法计算量较大，不适应实时性要求高的情况。文献［6］提出了根据小波分解到各个频带信号峭度来确定滤波阈值的改进算法，在对轴承故障信号的提取中取得了很好效果。文献［7］把各个频带能量用于滤波阈值的改进，大幅提高了语音信号的识别准确度。这两种算法都是结合信号自身特征来改进阈值，去噪针对性很强。受这两种算法启发，本文结合惯性传感器信号噪声特征对小波阈值进行了改进。

对于惯性传感器来说，通常用Allan方差来评价算法的去噪效果，也就是通过判断去噪后各个噪声系数下降的程度来评判去噪能力强弱［8-10］。因此本文提出将Allan方差辨识的噪声系数引入到阈值选择中去，对特定噪声系数进行有针对性的精准去噪。通过仿真和对半球谐振陀螺HRG（Hemispheri⁃cal Resonator Gyro）的线振动试验信号的处理，证明该方法确实能大幅抑制噪声，更加准确的对有用信号进行提取。

1 基本概念

1.1 Allan方差

Allan方差是一种经典的用于时域稳定性分析的统计方法，其主要特点是能够比较容易的表征和辨识出各种随机误差源的统计特性，是IEEE公认的陀螺参数分析标准方法，也可用于加速度计的噪声特性分析［10］。假设陀螺各噪声在统计意义上互不相关，且分布于不同频段，Allan方差可以表示为各类噪声的平方和。如式（1）

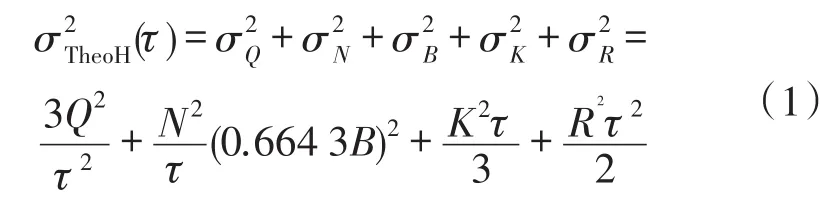
1.2 提升小波变换

提升小波变换（Lifting Wavelet Transform）是一种不依赖于傅里叶变换的较新的小波变换方法，与传统小波变换依赖于傅里叶变换从频域来分析问题的角度不同，提升小波完全是在时域进行变换的。它可以使用许多线性、非线性或空间变化的预测和更新算子，可以确保变换的可逆性。提升小波变换不仅继承了传统小波变换的特性，而且在实现信号消噪方算法结构简单、解算速度快、内存空间占用少、可实现整数小波变换等优点［12］。

2 基于Allan方差的阈值改进

在小波去噪方法中，提高算法滤波性能通常从小波基函数、阈值和阈值函数这三个方面入手。其中阈值选取的好坏直接影响去噪的效果，如果设定的阈值较大，可以消除更多的噪声，但同时也会把有用的高频信息当成噪声去除，造成信号失真；如果阈值过小，会保留较多有用信号小波系数，但同时也保留了较多的噪声，达不到良好的辨识效果。

2.1 阈值去噪方法

目前最常用的阈值值是Donoho等人提出的通用阈值，该阈值计算量小，应用范围广：

式中：σ是噪声标准差，N表示信号的长度。然而，Donoho阈值只是最优阈值的上限而非最优阈值，在滤波过程中经常会因为其量值过大，致使有用信息也被滤除。通常情况下，我们假设噪声信号是随机的，经小波分解后，噪声在高频尺度内分布较多，且随着分解尺度的增加，噪声信号的小波系数越来越少；而有用信号主要分布在低频尺度上。大多数阈值和阈值函数的改进算法也是基于这个原则，与信号自身没有关联。机械故障信号经常表现出较强的冲击、振动特征，峭度对此非常敏感，文献［5］用峭度改进了滤波阈值，用于对轴承信号进行分析。能量是评价语音信号强弱的重要指标，文献［6］用各频带信号能量来确定滤波阈值的大小。

而对于惯性传感器来说，Allan方差辨识出的噪声系数是评价滤波效果的重要指标，将其同阈值的确定关联起来，有针对性的对特定噪声进行消除，必然能够有效降低惯性传感器噪声系数的量值。基于此构想，本文提出了改进的Donoho阈值来对惯性传感器量测信号的小波分解系数进行处理，在改进算法中我们让每一层频带信号都有专属于自己的阈值Thr(j)，如公式（3）：

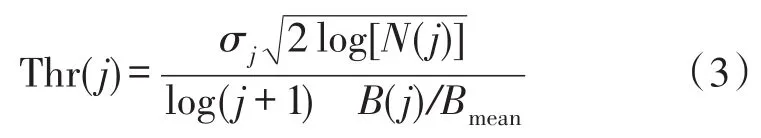
2.2 阈值函数的选择

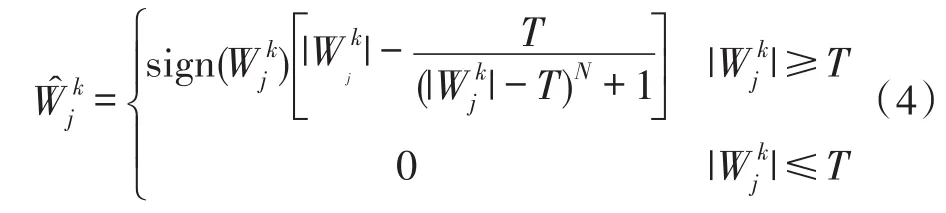
常用的软阈值函数存在固定的偏差，硬阈值函数会带来Gibbs振荡和整体不联续的问题，这里用文献［5］提出的新阈值函数来对阈值进行处理，该函数在保证了连续性的前提下，可以通过调节N来自由选择靠近软阈值函数还是硬阈值函数，如式（4）。

2 基于提升小波的滤波算法设计

提升算法首先使用多项式插补的方法获得信号的高频系数，然后通过某种约束条件获取信号的低频系数。提升小波变换的结构分为分解、预测和更新。分裂的目的是将原信号序列分为两个互不相交子集，获得该信号偶序列和奇序列的z变换e(z)和o(z)；然后通过预测因子u1(z)由奇序列o(z)预测偶序列e(z)；再通过更新因子 p1(z)用更新误差更新奇序列如此反复进行提升与对偶提升，最后再用1/K修正偶序列，用K修正奇序列完成一层小波变换。图1给出了构造基于提升方案的去噪算法一层分解重构去噪工作原理流程图。

图1 提升小波滤波算法工作原理框图

①分裂变换

②提升与对偶提升，For i=0 to m

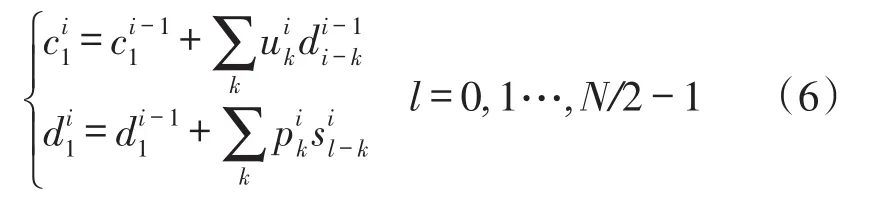
③比例变换，For l=0 to N/2-1

式中:m为分裂的总次数，最后得到的c和d分别为低频和高频分量，其中c={c0,c1,…,cN/2-1}，d={d0, d1,…,dN/2-1}。保留低频分量，对高频分量中的有用信号用前面提到的改进阈值和阈值函数进行滤波，重构时，首先逆更新恢复出偶数序列，然后逆预测恢复出奇数序列，最后将奇数序列与偶数序列交叉放置，重构出原始信号。下面我们通过仿真信号和加速度计动态试验信号对算法进行验证。

3 仿真验证

［13］的惯性传感器仿真模型，用Mat⁃lab自带的wnoise2与高斯白噪声叠加来模拟其动态输出，这样输出信号就会具有较强的非平稳性。给原始信号加入的高斯白噪声分别为5 dB和20 dB，原始信号与叠加了干扰后信号如图2所示。

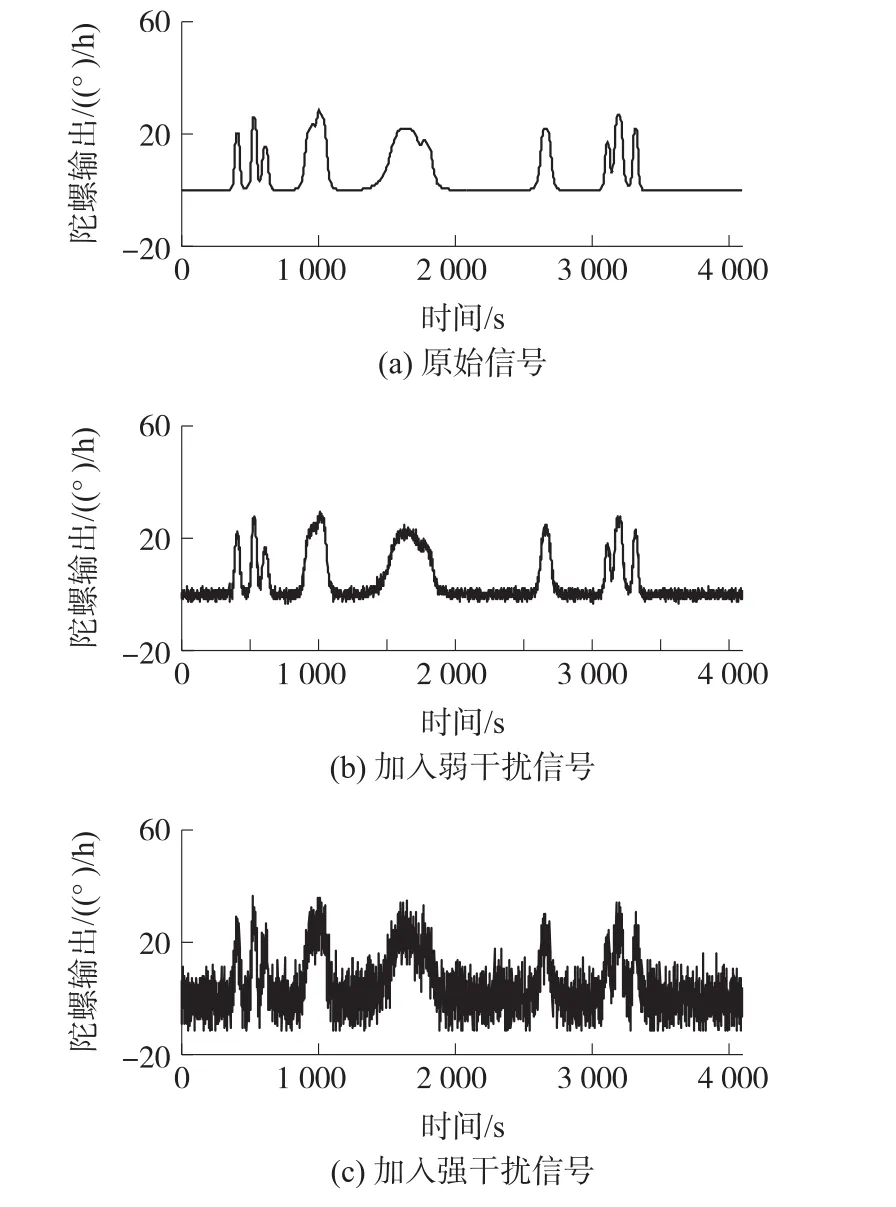
图2 仿真信号及其加噪后信号

对信号分别进行软阈值、峭度阈值和改进阈值提升小波滤波，小波基为db4，分解层数为4层。图3为对弱干扰仿真信号第一个波峰的顶部（也就是400到420时间点的信号）去噪后得到的比较图，可以看到改进阈值滤波方法明显比软阈值和峭度阈值方法能更准确的逼近真实信号。

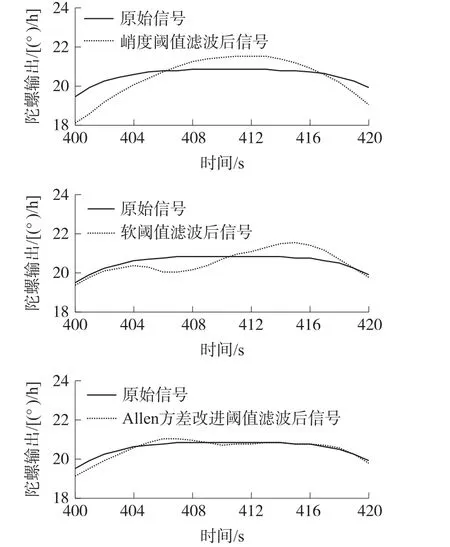
图3 加噪信号第一个波峰滤波效果比较图

对于仿真信号来说，用标准差和信噪比来评价滤波效果是更为科学的方法，因为仿真模型相当于真实信号是已知的，我们要做的就是比较滤波后信号与真实信号在幅值和能量上的差别，不同去噪算法处理后信号的标准差和信噪比如表1所示。

表1 振动条件下噪声系数的方差估计值

可见本文算法不管是在强噪声还是弱噪声条件下，即使以信噪比和标准差为评价函数，依然可以取得很好的效果。

4 HRG线振动试验信号分析

半球谐振陀螺（HRG）是一种基于哥氏效应的陀螺仪，具有较强的抗振动及抗冲击能力。本文以71号陀螺在线振动试验中采集到的角速率量测信号为原始数据，振动试验初始加速度为5 g，线振动频率约为1.7 Hz，采样时间为0.1 s，采集数据6 123个。为了验证本文算法的滤波性能，分别将该量测信号用kalman滤波、前向线性滤波FLP（Forward Liner Prediction）、文献［5］中提出的基于峭度的小波滤波方法和本文提出的改进阈值滤波算法进行去噪，并用Allan方差对去噪结果进行对比。（在没有真实基准信号的情况下，是无法用标准差和信噪比来评价去噪效果的）。

图4 HRG线振动试验量测信号及其频谱图

因为我们做的是恒定频率的线振动试验，理论上只有启动和停止振动的过程是非平稳的，也就是说陀螺真实输出有两个时段会有较大变化，一是由静态过渡到平稳振动时段（采样点1 300～1 800），二是由平稳振动回到静态过程时段（采样点4 000～4 600），其余时间应该都是相对平稳的随机过程［13］。用上一节提到的方法对采集到的信号进行滤波去噪，结果如图5所示。

可以看到，本文方法既大幅去除了信号中包含的噪声，又较好的保留了真实的有用信号。本文所定义的有用信号实际上是陀螺仪量测信号经过去噪（滤波）处理后的结果，可以认为是对陀螺实际输出有影响的随机漂移分量。效果比较好的还有基于峭度改进阈值的小波去噪方法，但该方法虽然将信号几乎滤波成了一条直线，但噪声系数下降的幅度却没有Allan阈值方法大，有用信号丢失较多，像振动开始和结束时的非平稳变化都没有提取出来。

从表2和图6中也可以看到：峭度阈值在噪声抑制尤其是高频噪声抑制上比Allan阈值改进算法要差一些。FLP滤波方法虽然大幅的降低了B、K和R这3个低频噪声系数，但对高频噪声系数的滤波能力实在太差，我们知道惯性传感器的真实输出大多位于低频段，高频信号是必须要去除的。具体各个算法的去噪结果如表2所示。

图5 不同方法去噪效果图

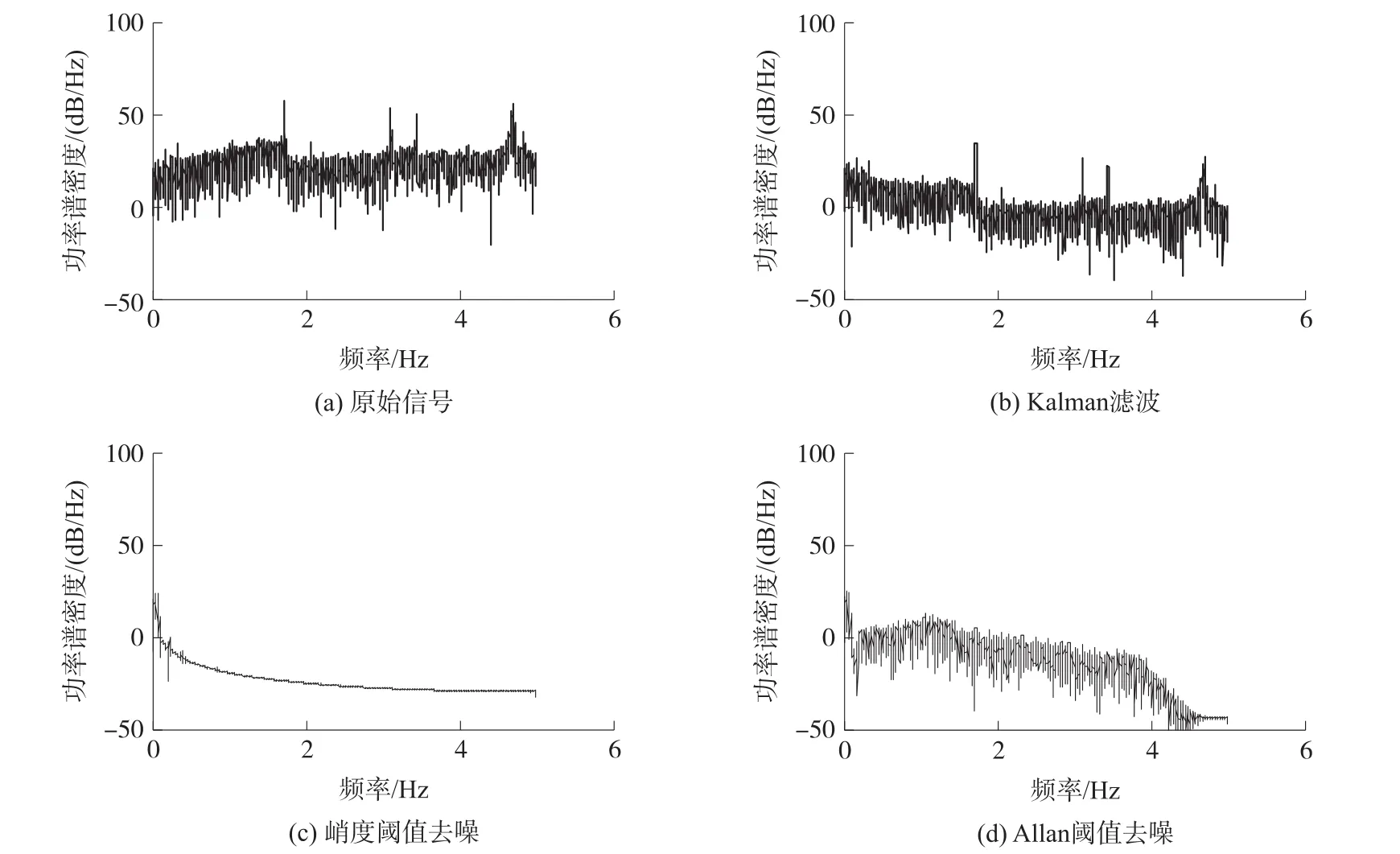
图6 不同方法去噪后功率谱密度分析图

表2 稳定条件下噪声系数的估计值

5 结论

本文提出了一种将去噪性能评价参数直接引入到去噪过程控制中去的小波阈值去噪改进算法。通过对仿真信号和HRG线振动试验实测数据的处理，证明该方法对动态条件下的惯性传感器量测信号去噪效果显著。该算法具有以下几个特点。

①针对性强，我们把Allan方差分离出的噪声系数作为滤波阈值选取依据，使降噪过程控制与降噪评价直接关联，有效去除了惯性传感器中包含的随机噪声。

②用提升小波包分解原始信号，大大提高了运算速度，有利于实时滤波的实现。

③本文的阈值计算函数是经提出者反复调试得到的，不一定是最好的。结合去噪评价参数，研究人员一定能提出更好的阈值计算函数。

④本文算法对惯性传感器动态信号具有良好的去噪效果，对于静态信号来说，一些能够精确建模的Kalman滤波改进算法效果可能会更好。

［1］方琳，申冲，陈熙源.基于小波多尺度变换的光纤陀螺振动误差分析与补偿［J］.传感技术学报，2012，25（7）：902-906.

［2］唐炜.颤振试验中加速度计信号的时频滤波方法研究［J］.传感技术学报，2009，22（2）：219-224.

［3］刘晓光，胡静涛，高雷，等.基于改进小波阈值的微机械陀螺去噪方法［J］.中国惯性技术学报，2014，22（2）：233-236.

［4］李佳桐，张春熹，张指挥，等.振动基座下光纤陀螺信号消噪方法对比研究［J］.现代电子技术，2014，37（4）：156-162.

［5］董明，贾学东，陈坡，等基于广义交叉验证的光纤陀螺动态信号小波阈值去噪［J］.信息工程大学学报，2011，12（4）：482-487.

［6］隋文涛，张丹.基于峭度的阈值降噪方法及在振动信号分析中的应用［J］.振动与冲击，2013，32（7）：155-158.

［7］殷明，孔冉冉.基于可调Q-因子小波变换的语音增强算法［J］.计算机应用研究，2014，31（11）：3316-3319.

［8］田云鹏，杨小军，郭云曾，等.光纤陀螺随机噪声滤波分析［J］.光学学报，2015，35（9）：0906006.

［9］崔冰波，陈熙源，龚政仰.基于经验模态概率分布的光纤陀螺信号处理［J］.中国惯性技术学报，2015，23（5）：690-695.

［10］宋海滨，杨平，徐立波.MEMS传感器随机误差分析及处理［J］.传感技术学报，2013，26（12）：1719-1723.

［11］李瑶，徐晓苏，陈臣.一种光纤陀螺漂移数据建模和滤波技术在捷联罗经法自对准中的应用［J］.控制与决策，2015，30（5）：934-938.

［12］栗鸣，郭东敏，权建峰，等.基于提升小波的改进半软阈值降噪方法［J］.探测与控制学报，2009，31（4）：54-57.

［13］Gan Y，Sui L F，Wu J F，et al.An EMD Threshold De-Noising Method for Inertial Sensors［J］.Measurement，2014，49：4-41.

［14］朱战辉，汪立新，李灿.动态总方差及其在陀螺振动信号分析中的应用［J］.传感技术学报，2015，28（12）：1789-1794.

朱战辉（1978-），男，河南人，博士研究生，控制科学与工程专业，主要研究方向为惯性系统及测试，数字信号处理，zzhhit@sina.com；

汪立新（1966-），男，湖北人，博士学位，教授，博士生导师，主要研究方向为惯性技术、组合导航及信号测试与处理，wlxxian@163.com。

Wavelet De-Noising of Inertial Sensor Dynamic Signal Based on Improvement Threshold with Allan Variance*

ZHU Zhanhui1，2，ZHANG Youni2，WANG Lixin1*，QU Yunxing2
（1.The Rocket Force University of Engineer，Xi’an 710025，China；2.Unit 96401 of the Chinese People’s Liberation Army，Baoji Shaanxi 721006，China）

The noise reduction effect of inertial sensor is usually evaluated by the Allan variance.Therefore，an im⁃proved wavelet threshold algorithm based on Allan variance noise coefficients is proposed.Firstly，the signal is de⁃composed into different frequency bands by lifting wavelet transform.And then the Allan variance noise coefficients of are calculated，their values are used in determining the filtering threshold.The improved algorithm has strong per⁃tinence，because the evaluation parameters of the de-noising effect are used to modify the threshold.Compare to oth⁃er inertial sensor de-noising methods.The proposed method can effectively suppress random noise to extract more accurate inertial sensor dynamic output.

inertial sensor；dynamic signal；wavelet threshold de-noising；Allan variance；noise coefficient

TP393

A

1004-1699（2016）11-1718-06

EEACC：7230；7310G 10.3969/j.issn.1004-1699.2016.11.015

项目来源：国家自然科学基金项目（61503390）

2016-03-09 修改日期：2016-08-07