考虑不确定因素的关键输电断面分析

靳冰洁，梁晨

(1.广东电网发展研究院有限责任公司，广东 广州 510080；2.中国南方电网超高压输电公司检修试验中心，广东 广州 510663)



考虑不确定因素的关键输电断面分析

靳冰洁1，梁晨2

(1.广东电网发展研究院有限责任公司，广东 广州 510080；2.中国南方电网超高压输电公司检修试验中心，广东 广州 510663)

计及负荷与间歇式电源波动在网络中的传播特性，提出基于综合介数指标的系统关键支路辨识方法，用以全面反映特定运行环境、网络结构及运行方式下系统的薄弱环节。然后提出基于节点电气距离聚类的电网分区算法及其修正措施，避免漏选区内重要线路。最后，在电网分区的基础上根据输电断面特征选择关键支路主导的输电断面作为系统关键输电断面。IEEE 39节点系统算例验证了该方法的有效性。实际应用时，可根据不同时段的负荷或间歇式能源波动特性以及系统运行方式的变化随时搜索系统关键输电断面，为有针对性地采取系统安全控制措施提供依据。

综合介数；关键支路；电网分区；输电断面

现代电力系统具有规模庞大、元件复杂、随机因素众多等特性，给运行研究带来了困难和挑战[1]。输电断面作为大电网的重要安全特征而受到运行人员的广泛关注[2-5]。我国地域辽阔，能源分布不均匀，地区发展不平衡，输电线路承担着大规模、远距离送电的重要任务，容易成为电网运行的薄弱环节。关键输电断面的识别与分析，有利于运行人员掌握电网安全运行的重要信息，有针对性地实施安全保护措施。

负荷性质的多样化和间歇式能源的接入带来许多不确定因素，时刻威胁着系统的安全稳定运行。系统中各线路受负荷及间歇式电源波动特性的影响程度不同，将导致关键输电断面的识别结果与确定性环境下有所差异。因此，关键输电断面分析应计及不确定因素带来的影响。现有输电断面识别方法大多仅考虑电网结构特征及运行方式，对含不确定因素环境下的输电断面特征分析鲜有论及。

针对传统基于运行方式专家经验的输电断面选取方法难以适应运行方式变化的问题，已有很多文献提出输电断面自动识别方法。电网分区是发现关键输电断面的有效手段[6-7]，能够简化网络，降低全网搜索的工作量。然而现有分区方法大多基于某一特定原则，缺乏针对误差的修正措施，容易存在漏选区内关键线路的情况。基于过载或故障支路选择相关输电断面[8-9]是从电网安全控制角度分析问题的可行思路，此类方法主要依赖关键支路的选取，在通过关键支路的选取来甄别系统薄弱环节方面仍有待进一步深入研究。

本文在以上研究内容的基础上提出考虑不确定因素的关键输电断面识别方法。计及负荷与间歇式电源波动在网络中的传播特性，提出基于综合介数指标的系统关键支路辨识方法；在此基础上提出基于节点电气距离聚类的电网分区算法及其修正措施，避免漏选区内重要线路；最后，在电网分区的基础上根据输电断面特征选择关键支路主导的输电断面作为系统关键输电断面。值得指出的是，目前文献对输电断面的细节定义仍有差异，如一些文献认为输电断面是电网中的割集[6-7]，而另一些文献不这样认为[8-9]，本文采取前者说法。

1 考虑不确定因素的关键支路辨识

输电断面由电网中的部分支路组成，能反映电网中的薄弱环节[8]，对电力系统进行关键支路辨识能够发现系统中的薄弱支路，进而引导输电断面的选择。基于关键支路选择的输电断面能够集中反映电力系统中易受攻击或干扰而故障，或者故障后严重影响电能传输并直接威胁电网安全的薄弱环节。

介数指标已被广泛应用于电力系统关键线路辨识中[7,10-13]。传统介数方法通常基于最短路径传输的假设，无法准确反映电力系统实际运行状态；而加权介数[11]加虽考虑了电网自身拓扑结构的特点，但未反应系统当前运行状态；一些文献将网络结构与运行状态相结合，提出改进方法，如电气介数[12]、输电介数[7]、潮流介数[13]等。然而，以上方法均未考虑不确定性因素对系统安全运行的影响。

负荷或间歇式能源的波动性会随其在电网中的传播而威胁系统安全运行，而系统中各支路受其影响的程度不同。因此，关键支路的辨识应在网架结构及运行方式的基础上，计及不确定因素在网络中传播带来的影响。基于此，本文提出线路的综合介数指标Bc，其计算公式为

(1)

式中：i为发电节点，G为发电节点集合；j为负荷节点，D为负荷节点集合；eδi、eδj为反应发电节点i和负荷节点j功率误差传播影响的误差系数，δi、δj分别为换算到基准容量下的发电节点i和负荷节点j功率误差百分比；Gk.ij为发电-负荷节点对ij对支路k的功率传输转移分布因子(power transmission distribution factors，PTDF)[14]，反映节点对之间功率传输对线路的占用情况；Cij为发电-负荷节点对ij的最大传输容量。

(2)

(3)

式中：m、n为支路k两端节点编号；Xmi、Xmj、Xni和Xnj均为系统电纳矩阵的逆矩阵X中的元素；xk为支路k的电抗。

(4)

发电-负荷节点对之间的最大传输容量受限于发电节点功率和负荷节点功率中较小的值，反应了系统的发电和负荷水平对节点对ij传输容量的限制，因此将Cij作为发电-负荷节点对ij功率传输转移分布因子的传输容量权重。

综合介数指标综合考虑了电网的结构特征、运行方式以及系统中不确定因素的影响，其中，通过功率传输转移分布因子反映支路在系统各发电-负荷节点对之间功率传输的电网结构特征重要性，通过传输容量权重考虑当前运行方式下发电和负荷水平对节点对传输容量的限制，通过误差系数计及发电-负荷节点对功率传输过程中分布式电源和负荷波动在网络中传播给支路带来的影响。

基于综合介数的关键支路辨识应用于电力系统关键输电断面选取主要体现在两方面：一方面，将支路综合介数指标按照从大到小的顺序排列，选择综合介数最大的若干条线路作为主导线路，并选取其主导的输电断面作为关键输电断面；另一方面，选择Bc>ε1(ε1为预先设定的关键线路综合介数阈值)的线路形成关键线路集Lkey，用以对电网分区算法进行修正，使得关键支路被包含于分区间联络线中，而不至于在选择输电断面时被忽略。

2 基于节点聚类算法的电网分区

输电断面的选取方法很多，其本质仍是对电网结构特征的辨识过程[7]。对电网进行分区，在分区联络线中选择满足输电断面特征的线路集合，是对电力系统的一种有效降维，与在全网所有线路中搜索输电断面相比，工作量大为减少，利于实际应用。

已有的基于系统分区的输电断面选取算法中，文献[6]以地理分区作为电网初始分区，对系统运行方式的适应性稍差；文献[7]基于分裂类算法对电网进行划分，虽然能够保证关键线路在分区之间，但无法保证分区内的节点之间相互联系紧密。电网分区既要保证分区内节点之间相互联系紧密，又要避免将关键线路和长程线路[7]划分区内而在选取输电断面时将其忽略。为此，有必要对基于聚类算法的分区结果进行修正，使其同时满足以上两点要求。

综上，本文提出基于节点聚类算法及其修正方法的电网分区方法，分为初步分区和最终分区两个过程。其中，初步分区根据节点之间的电气距离进行聚类，最终分区根据系统关键线路集和长程线路集对初步分区结果进行修正。

2.1 电网初步分区

基于电气距离的系统节点聚类算法既能体现网络的拓扑结构特征，又能考虑到网络的电气特点。具体表现在：电气距离较小的节点在拓扑结构中距离较近，通常在同一片区域内。

节点电气距离矩阵D中元素计算如下：

(5)

式中：Dst为节点s和节点t之间的电气距离；Zss、Ztt和Zst分别为阻抗矩阵Z中对应元素。

按照下述步骤对系统节点进行聚类：

a) 将第一个节点归为第一类。

b) 对于除第一个节点外的任一节点s，根据节点电气距离矩阵D得到已有各个分类中的节点与节点s之间的最大电气距离Ds.rmax，其中r=1，…，u为已存在的类别编号，u为已存在的类别数目。若对于任何一个已有类别r，均有Ds.rmax>ε2(ε2为预先设定的电气距离阈值)，则节点s不属于任何一个已有类，将其自身作为一个新的类；否则，节点s属于一个已有的类别。

c) 若存在一个已有类别r满足Ds.rmax<ε1，则节点s属于类别r；若有两个或两个以上已有类别满足该条件，则分别计算节点s与满足条件的各个类别的平均电气距离Ds.ravg(即类别内各个节点与节点s之间电气距离的平均值)，取其最小值所对应的类别作为节点s的所属类别。

d) 遍历系统所有节点，同一类内节点为一个分区，不同类内节点为不同分区，形成电网初步分区。

2.2 电网最终分区

聚类方法能从整体上反应所研究问题的关键特点，但通常存在误差，如系统中部分长程线路或关键线路本应是重点分析对象，若将其归为某一分区内，则会被忽略。本步骤旨在通过划分子区的方法辨识区域内长程线路或关键线路，并加以分析。

首先形成长程线路集Llong，Llong中的线路应满足xk>ε3(ε3为预先设定的线路长度阈值)；关键线路集Lkey按第一节所述方法形成。

对任一分区，若其中包含长程线路集Llong或关键线路集Lkey中的线路，则将线路两端节点分别划到两个子类中，该分区中其他节点按照与该两端节点之间电气距离的大小划分到两个子类中；若子类中仍包含长程线路集或关键线路集中的线路，则继续进行子类划分，直到每个类别中均不含有长程线路或关键线路。

考虑线路潮流方向，形成电网有向分区拓扑图。由于输电断面有潮流方向一致性的约束，可能存在两个或以上分区组成的分区组，其中任何两个分区由于潮流方向的限值均不可能被分在输电断面的两侧，则可将这样的分区组中的几个分区进行合并，以减少后续工作中不必要的工作量。

至此，电网最终分区形成，后续只需在分区间联络线中选择满足输电断面特征的线路集合构成输电断面，分析效率大大提高。

3 基于关键支路和电网分区的关键断面分析

前文阐述了关键线路辨识及电网分区方法，基于此，选择系统中最关键的若干条输电线路作为主导线路，并在电网最终分区的区域间联络线中选择主导线路所在的输电断面为关键输电断面。本文中输电断面所包含的线路集合应满足3个条件：输电断面包含的线路集合构成电网的割集；输电断面包含的各条线路有功潮流基本一致；主导线路开断对断面内其他线路影响较大。

以下为基于关键支路辨识和电网分区的关键输电断面选取步骤。

表1 不同情况下IEEE 39节点系统关键线路辨识结果(本文方法)

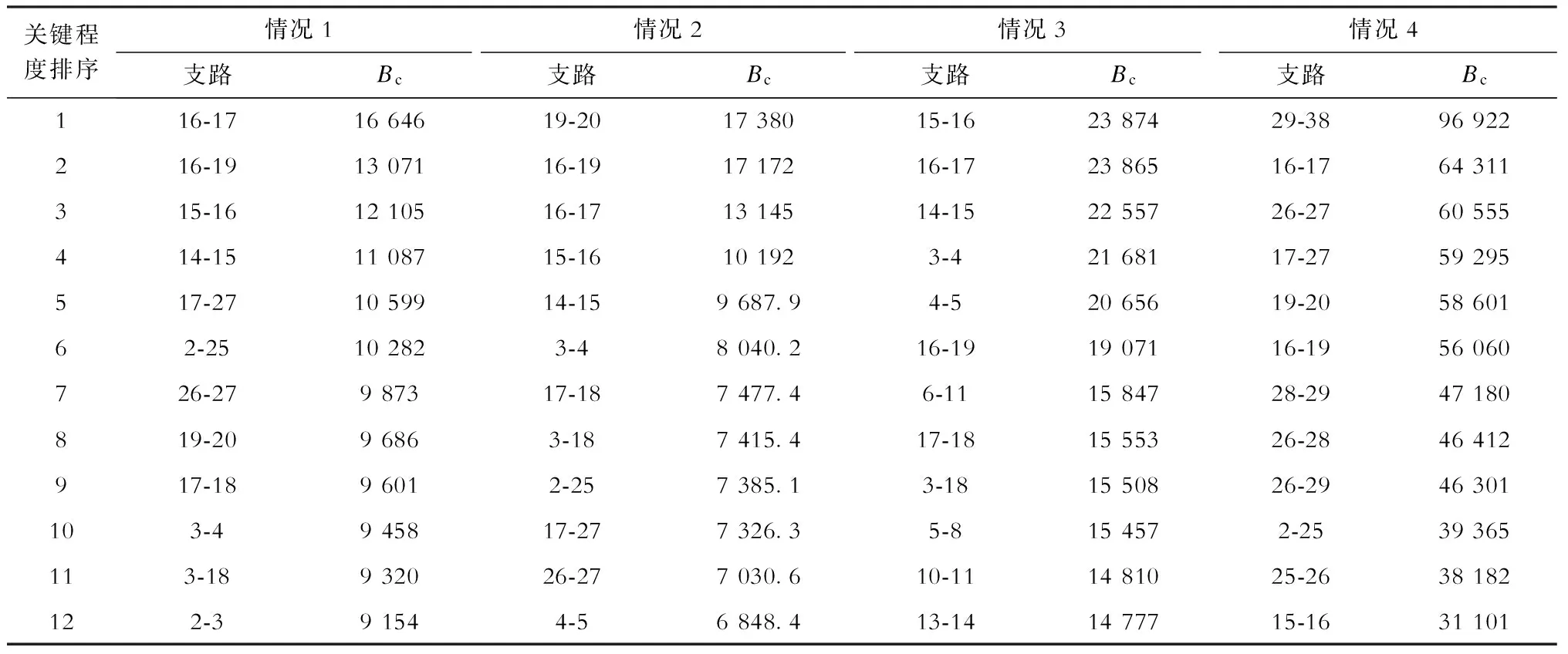
关键程度排序情况1支路Bc情况2支路Bc情况3支路Bc情况4支路Bc116-171664619-201738015-162387429-3896922216-191307116-191717216-172386516-1764311315-161210516-171314514-152255726-2760555414-151108715-16101923-42168117-2759295517-271059914-159687.94-52065619-205860162-25102823-48040.216-191907116-1956060726-27987317-187477.46-111584728-2947180819-2096863-187415.417-181555326-2846412917-1896012-257385.13-181550826-2946301103-4945817-277326.35-8154572-2539365113-18932026-277030.610-111481025-2638182122-391544-56848.413-141477715-1631101

注：“a-b”表示两端节点编号为a、b的支路，下同。

a) 选取主导线路。计算所有线路的综合介数，选择综合介数最高的若干条关键线路作为主导线路。

b) 形成系统分区。按照基于节点聚类算法的电网分区方法形成电网最终分区，长程线路及关键线路均包含在最终分区的区域间联络线路中。

c) 确定受主导线路开断影响较大的线路集合。对于每一条主导线路l，计算其与其他任一区域间联络线h的支路开断分布因子

(6)

其中

(7)

式中：Mh和Ml分别为联络线h和支路l的节点-支路关联矢量；ηl=XMl；xh和xl分别为联络线h和支路l的电抗。

若Dh-l>ε4(ε4为预先设定的支路开断分布因子阈值)，则将联络线h列入支路l的强相关支路集，即联络线h与支路l之间的开断灵敏度较大。

d) 根据潮流方向基本一致性确定输电断面。在上一步选出的线路集合中搜索割集断面，并选择支路潮流方向基本一致的断面作为输电断面，所谓基本一致，就是在一定程度上允许个别支路潮流反向，即只要满足Pl.h<ε5Pl.max(Pl.h为反向支路的有功潮流，Pl.max为该断面各支路有功潮流中的最大值，ε5为预先设定的反向潮流阈值系数)，则仍然认为其构成输电断面。

e) 遍历所有主导线路完成关键输电断面的选取。

以上方法共涉及5个阈值，即关键线路综合介数阈值ε1、电气距离阈值ε2、线路长度阈值ε3、支路开断分布因子阈值ε4和反向潮流阈值系数ε5，这5个阈值可根据实际情况和具体分析需要设置，用以对关键线路、系统分区、长程连接线及关键断面的数目进行控制。

4 算例分析

为验证本文方法的有效性，在IEEE 39节点测试系统上进行仿真，该系统包含10个发电机节点和46条输电线路，如图1所示。

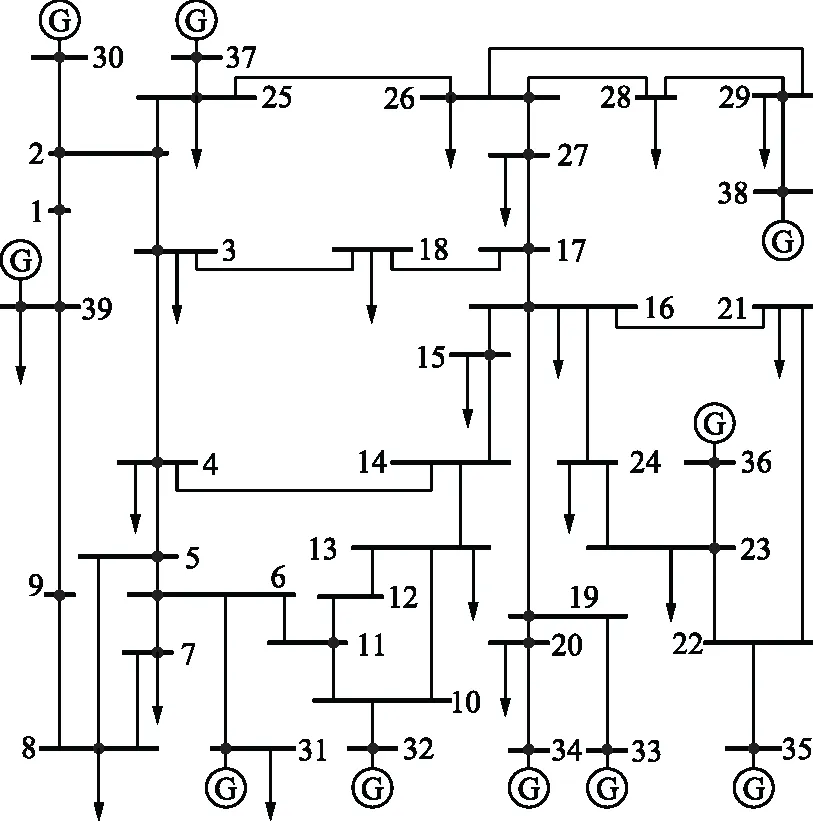
图1 IEEE 39节点系统

4.1 考虑不确定因素的电力系统关键线路辨识

本算例考虑以下4种情况：

a) 情况1，不考虑负荷和风电的功率波动；

b) 情况2，各个负荷节点功率的误差取5%；

c) 情况3，部分负荷节点功率的误差取8%，另一部分负荷节点功率的误差取3%；

d) 情况4，各个负荷节点功率的误差取5%，同时在节点38添加300 MW的风电功率，其误差取10%，该节点的常规机组出力相应减少300 MW。

4种情况下关键线路的辨识结果见表1。表2列举了几种现有方法的计算结果，这几种方法均未计及不确定因素的影响，故将其作为本例中情况1辨识结果的对比。

表2 不同方法下IEEE 39节点系统关键线路辨识结果

从表1情况1的结果和表2可以看出，在忽略不确定因素影响时，本文方法与文献[11，15-16]方法所得结果具有一定的相似性，其中支路15-16、16-17、16-19、14-15在3种对比方法中同时出现，说明其在系统中具有关键地位，本文方法不仅得出了同样的结论，而且在本文的排序中，这4条支路位列前4。从网络结构来看，支路26-27是发电机38功率外送的关键通道，也是发电机37功率外送的通道之一；从运行方式来看，发电机38的净输出功率是所有发电机中最大的，而其所在分区对系统主干网络的供电功率几乎全部通过支路26-27传送，综合考虑网络结构及运行方式，支路26-27应当成为关键支路，而该支路在表2所示3种对比方法中均被忽略。可见，本文所选关键线路在系统发电-负荷节点对之间的功率传输过程中，要么在网络结构中占据关键位置，要么在当前运行方式下承担了较重的传输任务，因而其重要程度较高。

从表1可看出，负荷节点和发电节点的功率波动会对关键支路的辨识结果产生影响。如支路 19-20 在情况2中关键程度排第1位，而在情况1中排在第8位，在情况3中没有排进前12位。从蒙特卡洛模拟得到的支路功率方差情况来看，情况2中该支路的方差排在第3位，表明该情况下其受负荷波动的影响较大，因此与情况1相比排名靠前，而情况3中该支路的方差排在第15位，表明该情况下其受负荷波动的影响不大，因此该情况下其关键程度未排在前面。支路16-19与支路19-20类似。支路29-38在情况1到情况3中关键程度排名均靠后，而在情况4中排在第1位，原因是在情况4中节点38接入了300 MW风电，其波动给该支路带来很大影响，从蒙特卡洛模拟结果来看，在情况2和情况3负荷波动情况下，该支路功率基本未受影响，两种情况下其功率波动方差均基本为零，而在情况4中其方差跃居第6位，说明其受风电功率波动影响很大。

4.2 电力系统分区

本算例中，取电气距离阈值ε1=0.018，关键线路综合介数阈值ε2=9 000，线路长度阈值ε3=0.017 7。电网分区结果如图2所示，关键线路集Lkey见表1情况1，长程线路集Llong见表3。

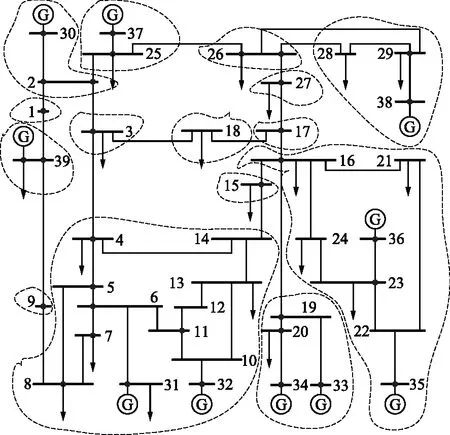
图2 IEEE 39节点系统分区图

表3 IEEE 39节点系统长程线路集

支路电抗标幺值支路电抗标幺值支路电抗标幺值1-20.04119-390.025025-260.03231-390.025014-150.021726-280.04743-40.021316-190.019526-290.06258-90.036323-240.0350

本算例将系统分为15个区，区域间联络线路包含了除线路19-20和线路23-24以外所有关键线路和长程线路(其中19-20为变压器支路，而23-24由于和16-21、21-22及22-23的潮流方向不一致而无法构成输电断面)。输电断面从区域间联络线中选取，既不会遗漏关键线路和长程线路，又有效降低了从全网中选取输电断面的工作量。本文所提聚类方法及其修正措施有效避免了关键线路的遗漏，同时，电气距离阈值ε1、关键线路综合介数阈值ε2和线路长度阈值ε3可根据实际情况和具体分析需要灵活设置，具有较强的适应性。

4.3 考虑不确定因素的电力系统关键输电断面选取

前面两个算例已验证了本文关键线路辨识和系统分区方法的合理性，在此基础上，本算例验证关键输电断面选取的合理性。支路开断分布因子阈值ε4和反向潮流阈值系数ε5可以根据实际情况和具体分析需要进行设置，本算例中ε4=0.2、ε5=0.18。4种情况下的关键输电断面选取结果见表4，其中粗体代表输电断面的主导线路。

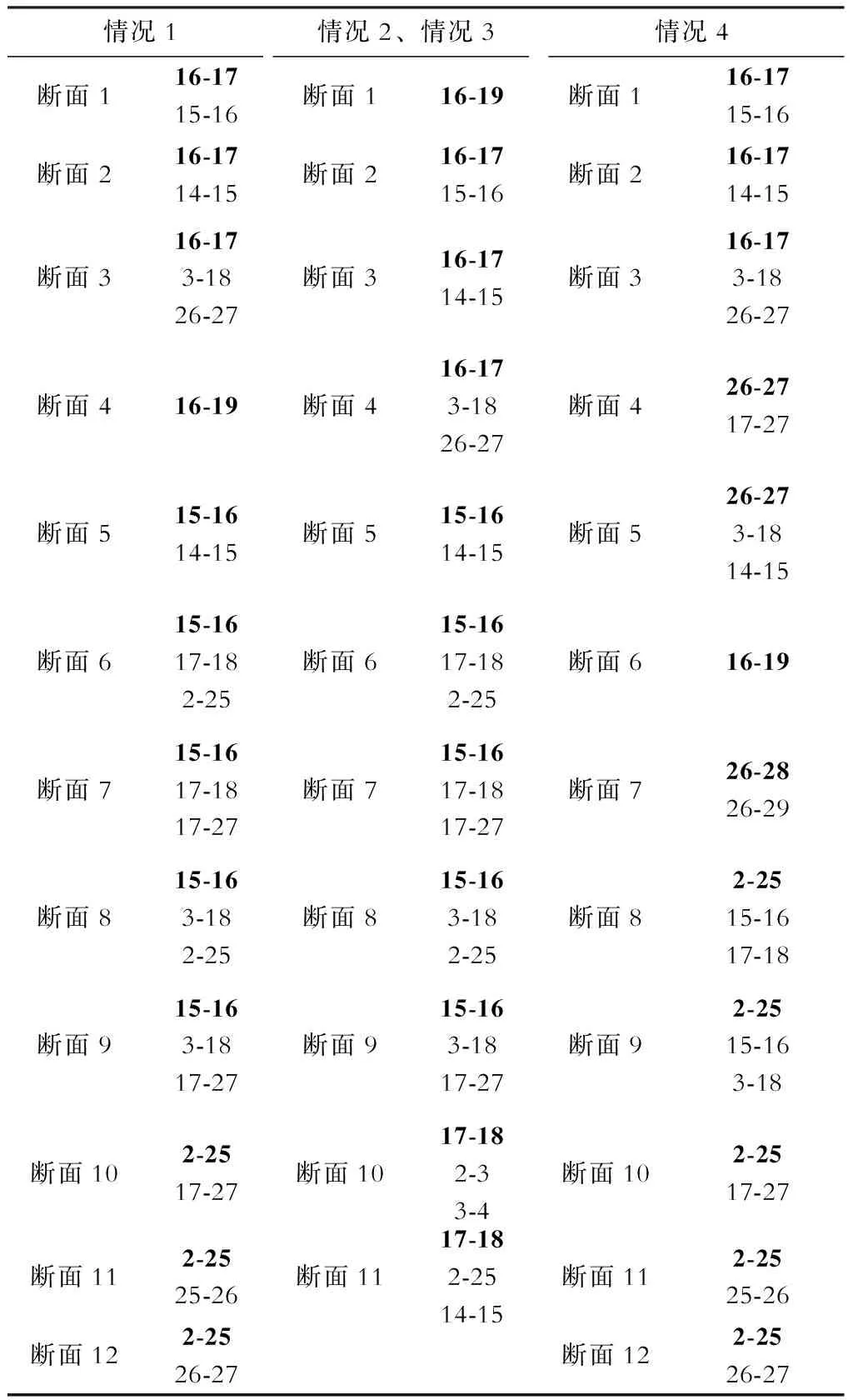
表4 不同情况下IEEE 39节点系统关键输电断面选取结果

从表4可以看出，负荷节点和发电节点的功率波动会对关键输电断面的选取结果产生影响。通过蒙特卡洛模拟得到各断面功率在不同情况下的方差及排序，用以说明不同波动下系统断面受不确定因素的影响程度。在所有关键输电断面中，情况2、情况3中断面11在该情况下方差排在第一位，表明其功率不确定程度很高，受负荷波动影响很大，因此该情况下将其列入关键断面；情况4中，断面11和断面12在该情况下方差显著增大，表明其受风电接入的影响很严重，因此该情况下将其列入关键断面。而以往方法中4种情况选取的关键断面结果相同，无法体现出系统中不确定因素带来的影响。

由表4还可看出，16-17和16-19主导的断面以及断面{2-25，15-16，17-18}和{2-25，15-16，3-18}在4种情况下均被选为关键输电断面，表明由网架结构及运行方式决定了其在不同运行环境下均对系统安全运行起到重要作用。

当一个断面功率的不确定性很大时，其安全程度的可信性将降低，其对系统安全带来的潜在危害不容忽视。算例说明本文方法所选断面不仅体现了其在常规潮流分析中的重要性，还反映了其受不确定因素影响的程度。

5 结论

本文计及负荷与间歇式电源波动在网络中的传播特性，提出考虑不确定因素的关键输电断面识别方法，该方法具有以下特点：

a) 综合介数指标综合考虑了网络结构、运行方式及环境中的不确定因素，将其应用于引导关键输电断面的选择，能够体现出不同运行环境下系统关键断面的差异。根据不同时段的负荷或间歇式能源波动特性以及系统运行方式的变化搜索系统关键输电断面，调整电网运行中的关注点，为有针对性地采取系统安全控制措施提供依据。

b) 所提电网分区算法，既保证了分区内节点之间相互联系紧密，又避免了将关键线路和长程线路划分区内而在选取输电断面时将其忽略。通过分区对电网进行简化，使搜索输电断面的工作量大为减少。

c) 关键线路综合介数阈值、电气距离阈值、线路长度阈值、支路开断分布因子阈值和反向潮流阈值系数可以根据实际情况和具体分析需要进行设置，增加了本文方法的灵活性和适用性。

[1] MEI Shengwei，ZHANG Xuemin，CAO Ming.Power Grid Complexity[M].Beijing：Tsinghua University Press，2011.

[2] LUO G，SHI D，CHEN J，et al.Automatic Identification of Transmission Sections Based on Complex Network Theory[J].Iet Generation Transmission & Distribution，2014，8(8)：1203-1210.

[3] 甘德树，欧思源，彭显刚，等.考虑风险和收益平衡的输电断面供电方案优化[J].广东电力，2014(3)：63-67.

GAN Deshu，OU Siyuan，PENG Xiangang，et al.Optimization for Power Transmission Section Power Supply Scheme Considering Risk and Profit Balance[J].Guangdong Electric Power，2014(3)：63-67.

[4] 张文朝，何玉龙，顾雪平，等.单输电通道中输电断面静稳极限的快速估算[J].电网技术，2012，36(5)：92-95.

ZHANG Wenchao，HE Yulong，GU Xueping，et al.A Fast Method to Estimate Steady-state Stability Limit of Tie Line in Single Power Transmission Channel[J].Power System Technology，2012，36(5)：92-95.

[5] 崔晓丹，方勇杰，周霞，等.基于风险的输电断面经济输电功率计算[J].电力系统自动化，2014，38(8)：30-34.

CUI Xiaodan，FANG Yongjie，ZHOU Xia，et al.Risk-based Economical Transmission Power Calculation of Transmission Sections[J].Automation of Electric Power Systems，2014，38(8)：30-34.

[6] 赵峰，孙宏斌，张伯明.基于电气分区的输电断面及其自动发现[J].电力系统自动化，2011，35(5)：42-47.

ZHAO Feng，SUN Hongbin，ZHANG Boming.Electrical Zone Division Based Automatic Discovery of Flowgates[J].Automation of Electric Power Systems，2011，35(5)：42-47.

[7] 罗钢，陈金富，石东源，等.基于复杂网络理论的关键输电断面分析[J].中国电机工程学报，2013，33(25)：147-155.

LUO Gang，CHEN Jinfu，SHI Dongyuan，et al.Key Transmission Sections Analysis Based on Complex Network Theory[J].Proceedings of the CSEE，2013，33(25)：147-155.

[8] 周德才，张保会，姚峰，等.基于图论的输电断面快速搜索[J].中国电机工程学报，2006，26(12)：32-38.

ZHOU Decai，ZHANG Baohui，YAO Feng，et al.Fast Search for Transmission Section Based on Graph Theory[J].Proceedings of the CSEE，2006，26(12)：32-38.

[9] 苗世洪，马帅，尚亚男，等.基于割点和路径搜索的输电断面快速识别方法[J].电力系统自动化，2014，38(2)：39-45.

MIAO Shihong，MA Shuai，SHANG Yanan，et al.A Fast Recognition Method of Transmission Section Based on Cut-vertex and Path Search[J].Automation of Electric Power Systems，2014，38(2)：39-45.

[10] KINNEY R，CRUCITTI P，ALBERT R，et al.Modeling Cascading Failures in the North American Power Grid[J].The European Physical Journal B：Condensed Matter Physics，2005，46(1)：101-107.

[11] 曹一家，陈晓钢，孙可.基于复杂网络理论的大型电力系统脆弱线路识别[J].电力自动化设备，2006，26(12)：1-5，31.

CAO Yijia，CHEN Xiaogang，SUN Ke.Identification of Vulnerable Lines in Power Grid Based on Complex Network Theory[J].Electric Power Automation Equipment，2006，26(12)：1-5，31.

[12] 程临燕，张保会，李光辉，等.采用有向电气介数的脆弱线路选取[J].西安交通大学学报，2011，45(6)：91-96.

CHENG Linyan，ZHANG Baohui，LI Guanghui，et al.Search for Vulnerable Line Based on Directed Electric Betweenness[J].Journal of Xi’an Jiaotong University，2011，45(6)：91-96.

[13] 刘文颖，梁才，徐鹏，等.基于潮流介数的电力系统关键线路辨识[J].中国电机工程学报，2013，33(31)：90-99.

LIU Wenying，LIANG Cai，XU Peng，et al.Identification of Critical Line in Power Systems Based on Flow Betweenness[J].Proceedings of the CSEE，2013，33(31)：90-99.

[14] 张伯明，陈寿孙，严正.高等电力网络分析[M].北京：清华大学出版社，2011：212-214.

[15] 鞠文云，李银红.基于最大流传输贡献度的电力网关键线路和节点辨识[J].电力系统自动化，2012，36(9)：6-12.

JU Wenyun，LI Yinhong.Identification of Critical Lines and Nodes in Power Grid Based on Maximum Flow Transmission Contribution Degree[J].Automation of Electric Power Systems，2012，36(9)：6-12.

[16] 丁明，过羿，张晶晶.基于效用风险熵的复杂电网连锁故障脆弱性辨识[J].电力系统自动化，2013，37(17)：52-57.

DING Ming，GUO Yi，ZHANG Jingjing.Vulnerability Identification for Cascading Failures of Complex Power Grid Based on Effect Risk Entropy[J].Automation of Electric Power Systems，2013，37(17)：52-57.

(编辑 彭艳)

Analysis on Key Power Transmission Section Considering Uncertain Factors

JIN Bingjie1, LIANG Chen2

(1.Guangdong Power Grid Development Research Institute Co., Ltd., Guangzhou, Guangdong 510080, China; 2.Maintenance & Test Center, UHV Power Transmission Company, CSG, Guangzhou, Guangdong 510663, China)

Considering propagation characteristics of load and batch power source fluctuation in network, this paper presents a method for key branch identification based on comprehensive betweenness which is used to fully reflect weak links of the system in particular operational environment or with specific network structure and running model.Then it proposes a power grid partitioning method based on node electrical distance clustering and its modification measures so as to avoid missing important lines.Finally, on the basis of grid partitioning and according to features of power transmission section, it selects key branch leading power transmission section as the key section of system.IEEE 39 node system example is used to verify effectiveness of this method.It is able to search for the key power transmission section according to load or batch energy fluctuation characteristic and system running mode at any time in actual application, so as to provide basis for adopting security control measures for the system.

comprehensive betweenness; key branch; power grid partitioning; power transmission section

2016-04-17

10.3969/j.issn.1007-290X.2016.11.023

TM 73

A

1007-290X(2016)11-0120-08

靳冰洁(1989)，女，河北蠡县人。工学硕士，主要研究方向为电力系统分析、规划。

梁晨(1989)，男，广东高州人。助理工程师，工学学士，主要研究方向为变压器类设备试验、技术监督和技术分析。